液压四足机器人足端的力预测控制与运动平稳性
李 冰 张永德 袁立鹏 朱光强 代雪松 苏文海
1.哈尔滨理工大学机械动力工程学院,哈尔滨,150080
2.哈尔滨工业大学机电工程学院,哈尔滨,150001
3.东北农业大学工程学院,哈尔滨,150030
0 引言
液压四足机器人以液压伺服系统为驱动原件,具有反应快、重量轻、尺寸小、结构紧凑及承受负载能力强等优点,在工业、农业运输等大负载场合广泛应用[1-2]。液压四足机器人足端与外界环境间的约束关系影响机身运动姿态的稳定性[3-4]。
目前,影响液压四足机器人运动姿态平稳性的足端力控制主要基于阻抗的控制策略。李鑫[5]、张国腾[6]采用基于惯性-刚度-阻尼模型的阻抗控制策略,通过调节阻抗模型参数使腿部的力柔顺,该液压伺服系统具有系统非线性及参数时变性等特点,足端位置力跟踪存在稳态误差。丁庆鹏[7]提出的自适应阻抗控制策略可对环境刚度及环境位置进行辨识,有效减小了足端位置力跟踪稳态误差,但存在响应延迟。苏文海等[8]提出一种基于复合粒子群自适应液压伺服系统力跟踪的阻抗控制策略,使液压伺服系统末端位置力跟踪的动态性能得到明显提高,能适应复杂的作业环境。此外,俞滨等[9]提出了基于液压驱动单元位置控制环的变刚度和变阻尼负载特性模拟方法,柯贤锋等[10]研究了基于力反馈的位置型主动柔顺控制方法,邵璇等[11]提出了基于动力学模型的机器人内力自适应抑制策略,柴汇[12]提出一种足端力柔顺控制方法。这些控制策略是根据液压四足机器人和液压伺服系统的动力学理论建立的,可以有效改善液压四足机器人腿部柔顺性和机身运动姿态的平稳性能。
上述学者对液压四足机器人腿部力控制与运动姿态平稳性的研究主要从力阻抗控制模型、动力学模型及模型的参数优化等方面展开。然而,液压四足机器人在坚硬路面行走时,足端位置受到的力是随时间不断变化的,且足端在接触地面瞬间存在刚性冲击,容易引起机身运动姿态的不平稳,故需要对液压四足机器人在坚硬路面行走时的足端受力情况进行研究。
为此,笔者提出一种液压四足机器人足端力预测控制方法。首先,根据液压四足机器人的结构进行运动学分析,得到足端位置相对于各腿关节转角的变换方程,求出雅可比矩阵,建立足端受到的地面作用力与关节力矩的关系式,采用基于复合粒子群自适应阻抗模型建立液压伺服系统末端位置的力闭环控制框架。然后,通过位置控制试验,得出大腿、小腿的液压缸位移曲线与足端力的变化曲线,采用改进自适应布谷鸟优化BP神经网络算法构建足端力预测控制模型。最后,结合液压四足机器人试验样机进行相关试验,验证液压四足机器人足端力预测控制方法的有效性。
1 液压四足机器人结构
液压四足机器人的模型如图1所示,其整体结构可表示为一种具有时变性特点的混联结构:当其单腿运动处于摆动相时,可被看作是串联机构;当其多腿支撑时,可视为具有冗余运动的并联机构[13]。

1.机身 2.机节 3.大腿 4.液压伺服系统 5.小腿 6.弹性元件
液压四足机器人主要由机身和4条相同结构的腿(安装方式为前肘后膝式[14-15])组成。每条腿由机节、大腿和小腿的3个液压缸驱动,其中,机节控制侧摆位移,大腿和小腿控制前进距离及抬腿高度。在足底部位安装弹性元件,减小液压四足机器人行走过程中落地时足端对腿部关节的强烈刚性冲击[16]。
2 数学模型的建立
2.1 运动学模型
建立液压四足机器人的单腿运动学模型是实现腿部关节转角与足端位置之间相互变换的常用分析方法,因此,采用D-H法、齐次变换来描述相邻连杆之间的运动学关系[17]。以左前腿为例,建立图2所示的连杆坐标系,图中,ObXbYbZb为机身坐标系,基坐标系O0X0Y0Z0建立在侧摆关节上,侧摆关节坐标系O1X1Y1Z1建立在基坐标上,大腿、小腿以及足端的坐标系O2X2Y2Z2、O3X3Y3Z3、O4X4Y4Z4分别建立在前一个连杆的末端上。关节坐标系的Zi(i=1,2,3,4)轴沿关节轴方向,Xi轴沿连杆方向,且足端坐标轴与小腿坐标轴的方向一致,各连杆变换参数如表1所示。

图2 液压四足机器人D-H坐标图

表1 液压四足机器人左前腿的D-H坐标参数
根据图2建立的运动学坐标及表1定义的参数,采用Paul变换法[18]得到液压四足机器人单腿运动学正解表达式:
0T4=0T11T22T33T4
(1)
(2)
s1=sinθ1s2=sinθ2c1=cosθ1c2=cosθ2
s23=sin(θ2+θ3)c23=cos(θ2+θ3)
式中,0T1为连杆1相对于基坐标的齐次变换矩阵;1T2为连杆2相对于连杆1坐标的齐次变换矩阵;2T3为连杆3相对于连杆2坐标的齐次变换矩阵;3T4为足底相对于连杆3坐标的齐次变换矩阵;0T4为足底相对于基坐标的齐次变换矩阵;a1为侧摆连杆长度;a2为大腿连杆长度;a3为小腿连杆长度。
由于液压四足机器人的每条腿有3个自由度,所以在对其正运动学方程求逆解时会存在多解,因而采用齐次矩阵的反变换法来求解液压四足机器人各腿的逆解。足端位置相对于侧摆关节角θ1、大腿关节角θ2、小腿关节角θ3的变换方程为
(3)
k1=pys1+pxc1-a1k2=-pzk3=a3s3
式中,px、py、pz分别为设定的足末端位置相对于基坐标系的侧摆位移、抬腿高度和前进距离。
2.2 力控制模型的建立
从控制角度来看,液压四足机器人的腿部机构是一个多变量、冗余、非线性的复杂力学系统,通过分析其足端位置力与关节力矩的对应关系,可建立图3所示的液压四足机器人足端力与关节力矩关系。

图3 足端力与关节力矩关系图
研究足端位置力与腿部关节力矩之间的变换关系是进行液压四足机器人腿部力控制、保持机身行走平稳性的前提和基础。若令足端位置的原点矢量p=(px,py,pz)T,关节转角θ=(θ1,θ2,θ3)T,则根据2.1节推出的运动学模型可知足端的运动轨迹与其关节转角之间的变换关系:
(4)
其中,J(θ)为3阶的雅可比矩阵,其列向量是足端位置对各关节转角的偏导。结合式(2)可得雅可比矩阵:
(5)
对单腿而言,我们假定液压四足机器人在模拟运行时,足端只受地面的支持力、摩擦力和机架水平反向的弹力,则根据虚功原理∑Fiδri=0(Fi为足端受到地面对它的合力,δri为虚位移)得到足端受到的地面作用力与关节力矩的关系[19]:
τ=JT(θ)F
(6)
式中,τ为腿部关节力矩,τ=(τ1,τ2,τ3)T;τ1、τ2、τ3分别为侧摆关节、大腿关节、小腿关节受到的力矩;F为作用在足端的地面反力(足端位置力),F=(Fx,Fy,Fz)T;Fx、Fy、Fz分别为足端位置受到相对于基坐标的三个方向反力。
液压四足机器人足端落地时,需要液压伺服系统末端位置受到的力准确跟踪期望力Fr,保持行走稳定性,故需要得到准确的足端位置力F的变化曲线,进而通过式(6)换成关节力矩,并根据余弦定理求出液压杆末端位置期望力Fr的变化曲线。
为保证液压伺服系统末端位置能够完成对期望力Fr的跟踪,采用基于位置的阻抗控制策略构成力闭环。该策略的力学公式为
(7)
式中,Md、Bd、Kd分别为液压伺服系统基于位置阻抗控制的期望惯性、期望阻尼和期望刚度的参数矩阵;Fe为液压伺服系统末端位置变化力;Δxm为期望位置偏差,Δxm=x-xr;x为当前位置;xr为期望位置。
因此,可得基于位置的液压伺服系统末端位置力跟踪阻抗控制框图(图4)。

图4 位置力跟踪阻抗控制框图
为保持液压伺服系统末端位置力跟踪的动态性能,本文采用苏文海等[8]提出的方法,研究基于位置的液压伺服系统力跟踪阻抗控制策略。
3 足端力预测控制模型的设计方法
足端力预测控制方法基于阻抗控制策略,并结合运动学模型与力学模型,将原有的跟踪固定期望力方式改为按步态周期跟踪实时变化的期望力方式来对足端力进行预测跟踪控制。这使得液压四足机器人在坚硬路面行走时,保证每条腿都能够始终处于合适的柔顺状态,有效减小液压四足机器人在坚硬路面行走时足端与地面的刚性冲击,提高液压四足机器人机身运动姿态的平稳性。足端力预测控制模型的设计方法如下:首先,采用液压四足机器人进行位置控制行走试验,得到液压伺服系统液压杆的位移与足端力的变化关系;然后,以液压四足机器人前进行走时的左前腿为例,根据改进自适应布谷鸟优化BP神经网络算法建立大腿、小腿的液压伺服系统位移变化量与足端力之间的关系函数。
3.1 试验方法
3.1.1试验样机简介
图5所示的液压四足机器人KL为试验对象。KL腿中的每个液压伺服系统包含位移传感器与力传感器,足端位置有六维力传感器,用来测试当前步态下的力/位关系。

图5 液压四足机器人KL
3.1.2控制系统设计
KL的控制系统包括监控计算机和上下位机。计算机作为监控计算机,用于数据的存储、监测与采集。
上位机将研华PC104作为主控制器,主要负责处理数据、控制运算和启停逻辑的控制;通过连接外置网卡与监控计算机通信;采用外置HCM-3680-CAN总线实现上位机与下位机的信号传递和数据接收。
4个下位机均以研华PC104为主控制器。下位机控制器的HIT-PC104-HXL-P515板卡用于采集每个关节的力/位置传感器信号,并进行A/D转换;HIT-PC104-HXL-P520板卡用于D/A转换,产生液压阀控制信号;各板卡的驱动模块均为基于MATLAB-2016a软件和嵌入式C++语言编写的MATLAB/Simulink S-Function模块。
此外,上下位机主控制器均将XPC系统作为实时操作控制系统。同时,整套控制程序的开发及控制算法的更改均在的MATLAB/Simulink框架下完成,一旦控制器确定程序,即可生成、固化、定型。
3.1.3试验过程
通过KL进行位置控制行走试验,试验场地为硬混凝土地面,试验步态为Trot步态,步态周期为2 s,控制器的采样时间为1 ms。以KL的左前腿为例,通过位移传感器、力传感器记录KL在一个步态运动周期内的驱动大腿、小腿液压缸的位移与足端力的变化数据,结果如图6所示。图6中,KL足端在处于摆动相时,足端力为0;处于支撑相时,足端力存在规律性的变化,最大值约为2130 N。

图6 左前腿液压缸位移与足端力的变化曲线
根据图6所示的试验结果,采用改进自适应布谷鸟优化BP神经网络算法对位置控制行走试验记录的数据进行网络训练,建立以大腿、小腿位移变化量为输入信号、足端力为输出信号的足端受力预测控制模型。
3.2 改进自适应布谷鸟优化BP神经网络算法的建立
3.2.1BP神经网络
根据文献[20-22]的研究可知,一个单隐含层的BP网络能够逼近任意一个闭区间内的连续函数,故采用BP神经网络对大腿、小腿液压缸位移与足端力的变化数据进行函数的构建。
本文构建的BP神经网络如图7所示,输入层节点数为2,隐含层节点数为3,输出层节点数为1;x1、x2为大腿液压缸位移变化的输入信号,Fr为足端处于支撑相时的预测力。

图7 BP神经网络结构图
图7所示BP神经网络算法的各层的输入、输出如下:
隐含层输入
Zj=w1jx1+w2jx2+bj
(8)
隐含层输出
oj=f1(Zj)
(9)
输出层输入
s=v1f1(o1)+v2f1(o2)+v3f1(o3)+a
(10)
输出层输出
Fr=f2(s)
(11)
式中,f1、f2为神经元活化函数,取正负对称的Sigmoid函数;wij(i=1,2;j=1,2,3)为输入层到隐含层的连接权值;bj为隐含层节点的阈值;vj为隐含层到输出层的连接权值;a为输出层节点的阈值。
3.2.2布谷鸟算法
BP神经网络在实际应用中容易陷入局部极值,学习、收敛慢,误差过大,每次训练时随机初始化的权值与阈值导致训练结果不一致。因此,本文采用布谷鸟搜索(cuckoo search,CS)算法(简称布谷鸟算法或CS算法)[23-25]优化BP神经网络阈值和权值[26-29]。布谷鸟算法原则如下:①种群中的每只布谷鸟每次产下一枚卵,并且随机选择一个其他鸟类的巢穴孵化卵;每个巢穴只接受一枚卵。②所有巢穴中,布谷鸟蛋质量最好的巢穴将被保留到下一代。③种群规模和鸟巢数量是一定的,宿主鸟发现布谷鸟卵的概率为Pa(0≤Pa≤1)。如果宿主鸟发现布谷鸟卵,则宿主鸟可以丢弃蛋或在新的地点建造一个新巢。
根据布谷鸟算法的上述三条原则可知,若巢穴存在布谷鸟蛋,则该巢穴被视作一个解,因此,布谷鸟搜索巢穴的路径和位置更新方式为
xt+1,i=xt,i+α⊕L(λ)
(12)
式中,xt,i、xt+1,i分别为t代、t+1代第i个巢穴的位置;α为搜索步长控制因子,用于控制布谷鸟的随机搜索范围;⨁表示点对点乘法;L(λ)表示莱维随机搜索路径。
布谷鸟进行莱维飞行的随机搜索路径与飞行时间t的关系服从Lévy分布:
L(λ) ~u=t-λ
(13)
式中,u服从正态分布;λ为幂次系数,1<λ≤ 3。
通过莱维飞行进行位置更新并随机产生0到1的数r,若r>Pa,则继续进行位置更新,否则保留上一代的最优解。
3.2.3改进自适应CS算法
在CS算法的参数中,步长控制因子α和发现概率Pa能帮助算法找到局部最优解和全局最优解,并调整CS算法的收敛速度[30]。传统CS算法将Pa和α设为定值,其主要缺点是迭代次数不确定,不能很好选择Pa和α。如果Pa较小、α较大,则算法性能较差,导致迭代次数大幅度增大;如果Pa较大、α较小,则收敛较快,但可能无法找到最佳解。
为了提高CS算法的性能并克服上述缺点,本文引入自适应改进CS策略,动态调整Pa和α。在CS算法前期,Pa和α的值足够大才能使算法增加解向量的多样性;当CS算法进入到中后期,Pa和α逐渐减小,从而提高搜索精度并保留适应值更好的解。Pa和α随生成次数动态改变:

(14)
(15)
式中,N、n分别为总迭代次数和当前迭代次数;qmin为当前最小适应度值;qavg为当前平均适应度值。
3.2.4适应度函数
采用BP神经网络算法对数据的输入和输出进行网络训练的本质是通过调节权值和阈值,让BP神经网络的实际输出值与期望输出值之间的误差达到最小。因此,本文采用改进CS算法优化BP神经网络,将改进CS算法的适应度函数作为优化的目标函数对BP神经网络的权重和阈值进行优化,从而提高足端受力预测控制模型的准确性。根据文献[27],本文选取改进布谷鸟算法的适应度函数为
(16)
式中,k为样本总数;y′(i)为第i个样本的实际训练输出值;y(i)为第i个样本的期望输出值。
3.2.5改进自适应布谷鸟优化BP神经网络算法
首先,根据样本数据维数确定BP神经网络的结构以及权重和阈值的总数,进而确定改进自适应布谷鸟算法中搜索空间的维数。其次,构造布谷鸟的鸟巢坐标与神经网络权重和阈值的对应关系,将待确定的权重和阈值视为改进自适应布谷鸟算法中有待寻找的鸟巢坐标,故所有鸟巢单体可以看成是权重和阈值的一个组合体,且任意一个鸟巢的好坏都由适应度函数决定。改进自适应布谷鸟算法的目标就是找到一个最优的鸟巢坐标,使选取的适应度函数得到最小值。最后,将该鸟巢坐标分量赋予BP神经网络的权重与阈值,用以构建优化后的BP神经网络。具体流程如图8所示。

图8 改进自适应布谷鸟优化BP神经网络算法流程图
4 仿真对比分析
为验证改进自适应布谷鸟优化BP神经网络算法的可行性,利用MATLAB 2016a软件编写程序,并以位置控制行走试验记录的大/小腿位移数据为输入信号,以足端力数据为训练目标进行仿真测试;同时,将改进自适应布谷鸟优化BP神经网络算法(改进自适应CS-BP算法)与现有的BP神经网络算法(BP算法)、Fuzzy优化BP神经网络算法(Fuzzy-BP算法)及PSO优化BP神经网络算法(PSO-BP算法)做仿真对比分析。对比结果如图9所示。

(a)BP算法
由图9a可以看出,采用BP算法构建的液压伺服系统位移变化量与足端力变换模型的预测力与测试力存在明显的跟踪误差,且在运行时间(步态周期)1s(1/2个步态周期)附近出现力信号振荡。由图9b、图9c可以看出,采用Fuzzy-BP算法及PSO-BP算法后,预测力与测试力之间的跟踪误差明显比BP神经网络的小,但运行时间(步态周期)1s附近依然存在振荡信号。图9d中,采用改进自适应CS-BP算法的预测力能够很好地对测试力进行跟踪,动态性能良好,且运行时间(步态周期)1s附近没有振荡信号出现,预测力与测试力之间的跟踪误差最小。仿真结果验证了改进自适应CS-BP神经网络算法的可行性,说明采用该算法构建的足端受力预测控制模型能满足液压四足机器人足端位置力的跟踪动态性能要求。
5 试验分析
5.1 足端柔顺力测试
当液压四足机器人在坚硬路面快速行走时,由于足端在触地的瞬间会产生较大的刚性冲击,故需要提高液压四足机器人腿部力柔顺性,进而改善机身姿态的平稳性。因此,为验证所提出控制方法对提高液压四足机器人腿部力柔顺性能的可行性,以及采用改进自适应CS-BP神经网络算法构建预测力控制模型的有效性,对液压四足机器人KL进行足端柔顺力测试。其中,控制系统的模型框图(图10)是在图4的基础上进行设计的。

图10 液压伺服系统控制框图
采用改进自适应CS-BP算法构建的预测期望力控制方式与跟踪固定期望力和BP算法、Fuzzy-BP算法、PSO-BP算法构建的预测期望力控制方式进行对比。试验过程中,采用Walk步态在硬混凝土地面做前进位移为0的抬腿运动,且步态周期时间分别选择0.5 s、0.75 s、1.0 s、1.25 s、1.5 s、1.75 s、2.0 s,测试液压四足机器人足端在触地瞬间时(足端触地后至1/10个步态周期)的受力最大值。试验结果如图11所示。

图11 足端柔顺力测试图
由图11可以看出,当液压四足机器人的步态周期时间逐渐缩短时,运动不断加快,足端在触地瞬间的受力最大值逐渐增大,且足端在跟踪固定期望力时的情况最明显。此外,当步态周期时间趋于2 s时,液压四足机器人腿部的运动较慢,受到地面的刚性冲击较弱,足端在触地瞬间(足端触地后至1/10个步态周期)的受力最大值也逐渐趋于稳定(约为100 N)。试验结果验证了采用足端力预测控制方法提高液压四足机器人腿部力柔顺性的可行性,能保证液压四足机器人在坚硬路面上快速行走时的运动姿态平稳性。
同时,结合图11可知,采用改进自适应CS-BP预测跟踪期望力控制的足端力最大值在不同步态速度下均趋于100 N,比BP算法、Fuzzy-BP算法、PSO-BP算法预测跟踪足端力的控制方式更稳定,腿部力柔顺性明显得到了改善;试验结果也验证了采用改进自适应CS-BP算法预测跟踪期望力控制的有效性。
5.2 刚性地面行走姿态平稳性测试
为验证上述理论对提高液压四足机器人在硬路面行走时的机身运动姿态平稳的有效性,将跟踪固定期望力方式、PSO-BP算法构建的预测期望力控制方式与改进自适应CS-BP算法构建的预测期望力控制方式进行对比分析。试验环境为混凝土地面。如图12所示,机器人腹部安装有支架,支架底部距离地面5 cm,防止期望力跟踪不稳时机器摔倒。选择Trot步态作为行走步态,步态周期为2 s,运行时间为30 s。液压四足机器人行走姿态的稳定性试验结果如图13所示。

图12 试验过程图片
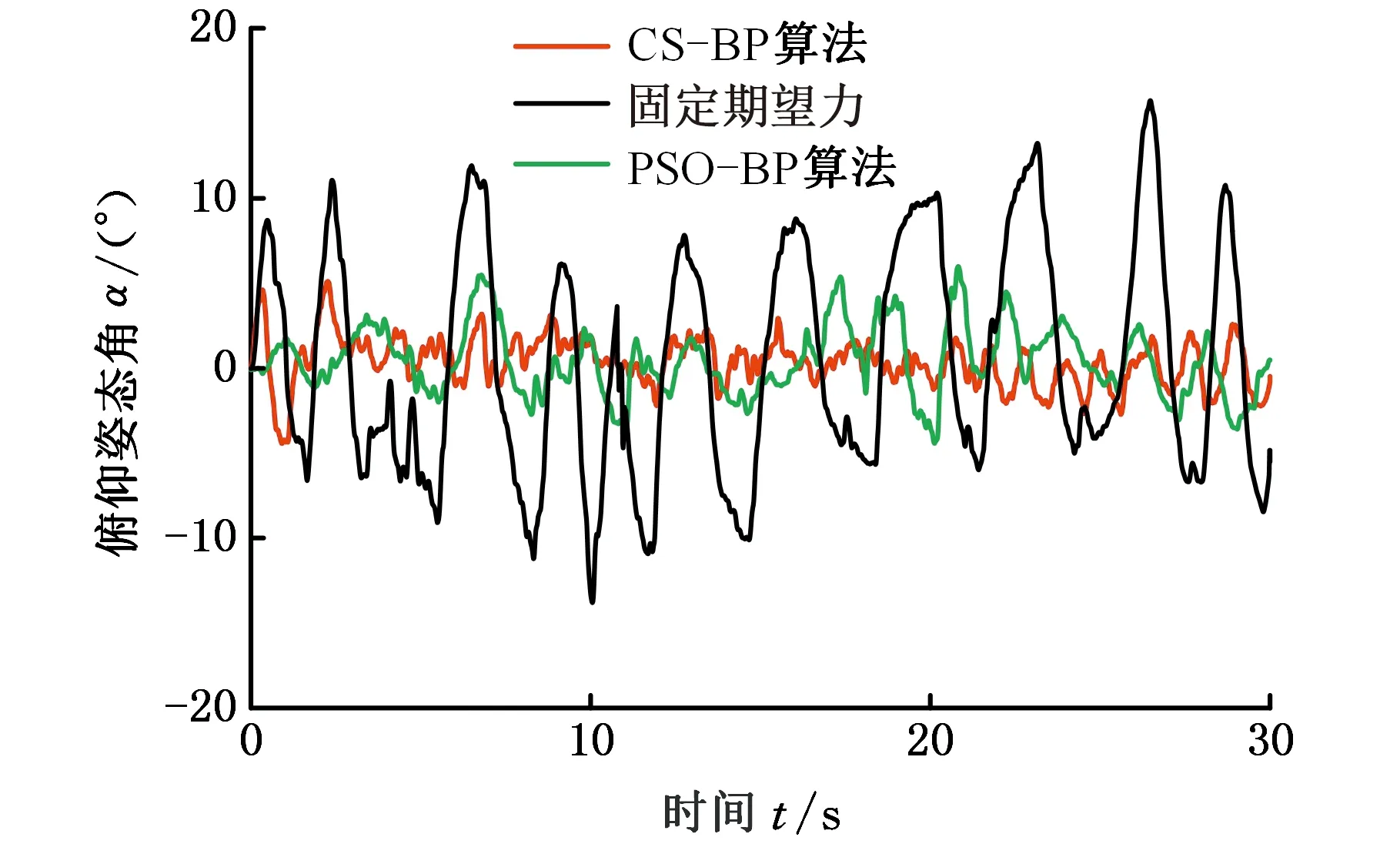
(a)俯仰姿态曲线
由图13a可以看出,采用固定足端期望力2000 N时,机身俯仰姿态角度α范围是-13.5°~13.5°;采用PSO-BP算法构建的足端力预测控制方式时,机身俯仰姿态角度α范围是-5°~5°;采用改进自适应CS-BP算法构建的足端力预测控制方式时,机身俯仰姿态角度α范围是-2.5°~2.5°。如图13b、图13c所示,采用改进自适应CS-BP算法构建的足端力预测控制方式时,机身翻转姿态角度β范围是-4.5°~4.5°,机身航偏姿态角度γ范围是-4°~4°,优于其他两种方法,验证了本文的控制方法能提高液压四足机器人在坚硬路面行走时的机身姿态稳定性。
6 结论
(1)本文提出一种液压四足机器人足端力预测控制方法,采用改进自适应CS-BP算法建立了液压四足机器人大腿、小腿的液压伺服系统位移变化量与足端力之间的预测控制模型,实现了液压四足机器人足端在支撑相位时的实时力跟踪控制。这使得液压四足机器人在坚硬路面行走时,每条腿都能够实时保持合适的柔顺性。
(2)借助MATLAB软件将改进自适应CS-BP算法训练的预测数据与现有的BP算法、Fuzzy-BP算法及PSO-BP算法训练的预测数据进行仿真对比分析,发现采用改进自适应CS-BP算法的足端预测力跟踪效果最优,说明采用该算法构建的足端受力预测控制模型能满足液压四足机器人足端位置力的跟踪动态性能要求。
(3)通过试验样机进行了足端柔顺力控制测试,发现改进自适应CS-BP算法控制足端位置期望力的跟踪性能最优,能有效减小足端与地面接触时的刚性冲击,提高腿部力柔顺性。
(4)试验样机平稳性测试证明,改进自适应CS-BP算法的性能优于固定期望力及PSO-BP算法,机身姿态俯仰、翻转、航偏角度大幅度减小,提高了液压四足机器人在坚硬路面行走时的机身姿态稳定性。

