基于非水平位移的激光跟踪仪测角误差标定方法*
李 辉,伍嘉豪,赵伟康,马大智,周志龙,于斌超,刘 巍
(大连理工大学 机械工程学院,辽宁 大连 116023)
激光跟踪仪具有测量范围大、单点测量精度高等优点,被广泛应用于航空航天装备制造过程中的大尺寸几何测量[1-2]。随着大型构件尺寸与制造精度的极值化,测量精度和可靠性的要求愈发提高。为了有效评估几何量测量结果的可靠性,需要对测量仪器的系统误差进行评估[3]。激光跟踪仪为非正交测量系统,通过干涉测长与2个角度编码器的角度测量,实现了球坐标系下三维坐标的测量。随着测量范围的增大,激光跟踪仪的测量精度下降,其中测角误差是影响激光跟踪仪测量精度的核心因素。因此,实现激光跟踪仪测角误差的有效标定对整体测量精度的准确评估至关重要。
目前,为了实现对激光跟踪仪测角误差的有效标定,众多专家学者依据激光跟踪仪的测量原理,使用标准杆、标准球等各种方法对激光跟踪仪的测角误差进行标定技术研究。佛罗里达大西洋大学的H. Zhuang等[4]针对激光跟踪仪内部各测量部件的几何误差,提出了一种基于单束干涉光的激光跟踪仪误差的运动学模型,通过一系列运动学几何参数表征激光跟踪仪内部各测量原件的几何误差,实现了对激光跟踪仪系统的设计、校准以及对测量误差的标定。西班牙萨拉戈萨军事学院的R. Acero等[5]通过序列计量平台完成了跟踪仪误差的标定。通过操控跟踪仪伴随平台旋转,将跟踪仪运动学模型与平台的数学模型融合,建立了跟踪仪误差标定模型。上述方法与传统的跟踪仪标定实验相比,不仅缩小了测量仪器体积,还缩短了测试时间。英国城市大学的T. A. Clarke等[6]基于激光跟踪仪的球坐标测量原理以及其内部结构,构建了以标准杆为约束的一维误差标定模型,完成了激光跟踪仪测量误差的标定。同时,利用该模型,验证了激光跟踪仪测长干涉精度、双束激光测量、ADM模式测量精度等指标。合肥工业大学的卢荣胜等[7]采用高精度多面反射棱镜与高精自准直仪,实现了对跟踪仪的测角误差的标定。长春光学精密机械与物理研究所的刘力等[8]提出了一种利用多项式获取跟踪仪测角误差的检测方法,拓展了其在大口径非球面镜检测中的应用。北京长城计量测试技术研究所的马骊群等[9]提出了一种基于位移的激光跟踪仪测角误差标定方法,可通过位移实现测角误差的有效标定,但该方法需调平激光跟踪仪,操作过程复杂且易引起误差。
为了同时兼顾标定精度与过程操作简便性,提出了一种基于非水平位移的激光跟踪仪测角误差标定方法,以空间任意高精运动位移为约束,采用三坐标测量机与高精位移台相结合的方式,分别对空间任意位移的角度与长度进行高精求解,实现了激光跟踪仪测角误差的快速有效标定。
1 激光跟踪仪测角误差的标定原理
1.1 激光跟踪仪测量原理
激光跟踪仪的测量原理为非正交系测量原理,其模型为球坐标系模型,包括1个干涉测长单元和2个测角单元(俯仰角和水平角)。然后,通过球坐标系与笛卡尔坐标系转换原理,获得被测空间点的三维坐标值(见图1)。
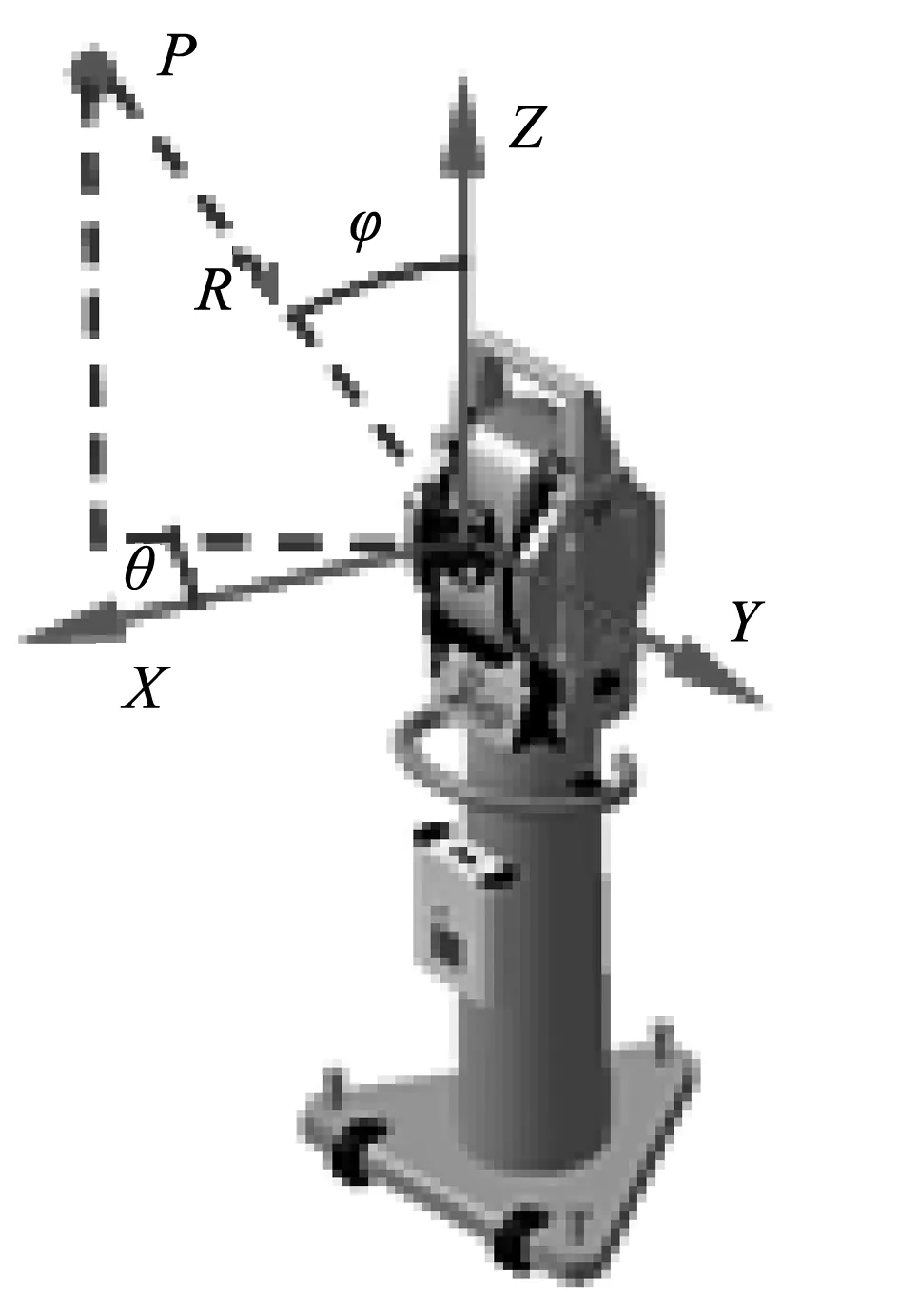
图1 激光跟踪仪测量原理
基于球坐标系与笛卡尔坐标系转换原理,求解笛卡尔坐标系下测点的三维坐标:
(1)
式中,R为测长误差;θ为水平角;φ为俯仰角。
由式1可知,笛卡尔坐标系下激光跟踪仪三维坐标测量误差是3个相互独立测量单元共同影响的结果[10-11],因此,各个测量单元的测量误差,都将不同程度地引起测量点的坐标误差。
根据式1,可推导出各测量单元误差与测点三维坐标误差的影响关系。将式1在理想点(R0,φ0,θ0)处一阶泰勒展开,假设测长传感器与测角传感器间相互独立,则:

(2)
由式2得出激光跟踪仪测量误差矩阵:
(3)
式中,T表示误差矩阵的系数矩阵,T=
1.2 激光跟踪仪测角标定原理
针对激光跟踪仪测角误差的标定,结合空间三角余弦定理,以激光跟踪仪测长距离为约束,实现角度误差的标定(见图2)。以水平角测量为例,通过对激光跟踪仪进行调平,在两位置测量时保证激光跟踪仪垂直角一致,利用测长为约束,实现水平角度的测量,对转角误差进行评估:
(4)

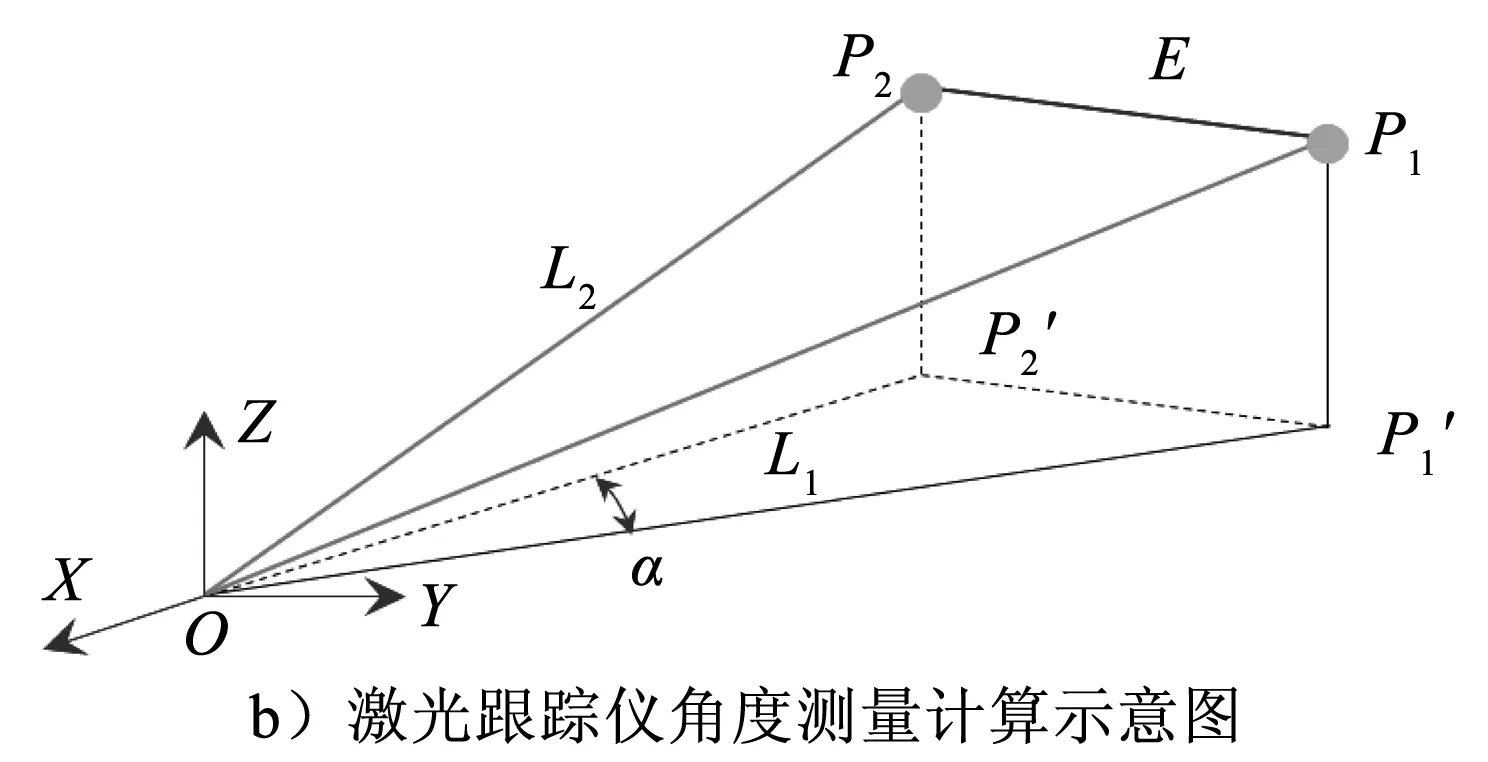
图2 激光跟踪仪的角度标定模型
2 基于非水平位移的激光跟踪仪测角误差标定

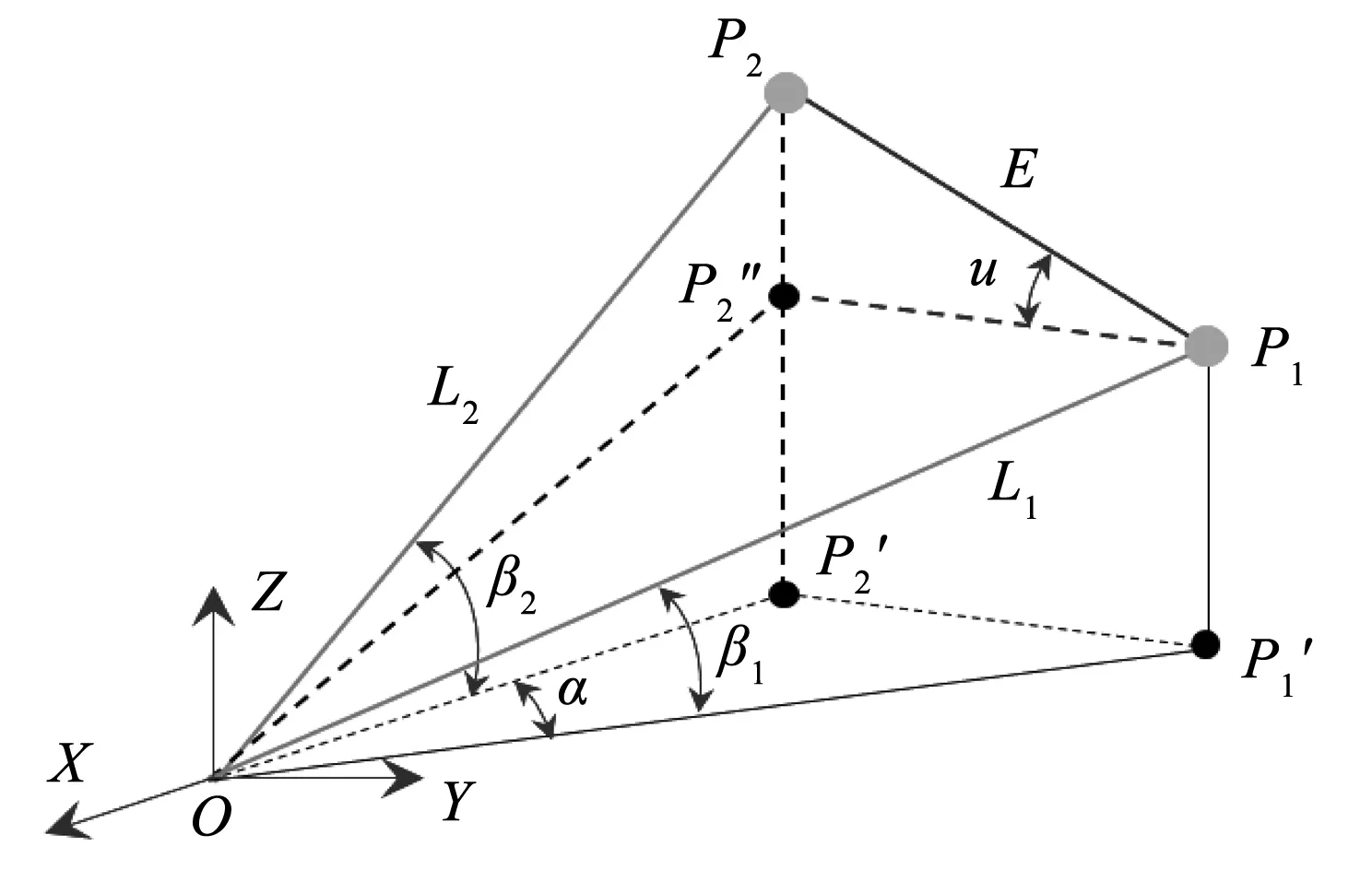
图3 激光跟踪仪空间任意测角标定
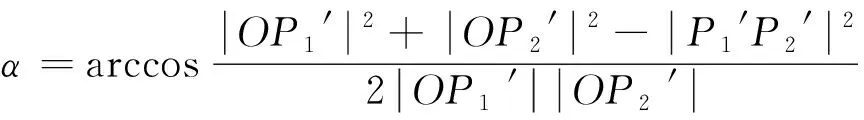
(5)
(6)

(7)
在水平角θ1-θ2的测量范围与俯仰角β1-β2的测量范围内,激光跟踪仪水平角累积误差、俯仰角累积误差分别为:
(8)
3 试验与分析
本文试验中所采用的激光跟踪器型号为Leica-AT960MR,配套0.5英寸靶球、1.5英寸靶球,其中干涉测距精度为0.5 μm/m,角度精度为5 μm+6 μm/m,激光跟踪仪整体测量精度为±(15 μm+6 μm/m)。具体试验测量设备如图4所示,主要包括蔡司三坐标测量机、PI平台、激光跟踪仪及配套的靶球与靶座、工作站及相关配套软件等。

图4 激光跟踪仪测角标定试验设备

标定距离设定为2 m。利用三坐标测量机获得点与水平面的空间运动方向为(0.985 2,-0.171 2,-0.008 7)获得具体的求解值(见表1)。

表1 激光跟踪仪角度测量误差标定试验结果
已知激光跟踪仪出厂标定的最大允许误差为±(15 μm+6 μm/m),单位测角误差为±(5 μm+6 μm/m),可转换为3.5″。通过表1(第8~第9列)计算可知,水平角平均误差为0.865″,俯仰角平均误差为2.6″,均在误差范围内。测量过程中靶球与夹具为磁连接,而且三坐标测量属于接触式测量,易引入干扰因素,导致测量精度下降。所以在考虑数据计算与激光跟踪仪标定过程的基础上,对于使用激光跟踪仪的局部小范围测量可以采用简单标定,测量过程中实际激光跟踪仪整体测量误差可取±(15 μm+6 μm/m)的0.45倍。
4 结语
针对激光跟踪仪测角误差的标定问题,提出了一种基于非水平位移的激光跟踪仪测角误差标定方法,实现了激光跟踪仪角度误差的高精有效标定。通过实验室试验,利用三坐标测量机、PI高精移动平台及激光跟踪仪的高精干涉测长构建了高精约束长度,实现了基于非水平位移长度的角度解算,完成了激光跟踪仪测角误差的有效评估,水平角平均误差为0.865″,俯仰角平均误差为2.6″。该方法可为激光跟踪仪、摄影测量、经纬仪等大尺寸测量设备的误差检验和精度校准提供借鉴。

