常见一次超静定梁力法基本体系的选取

陈 思 李文静 权 集

（燕京理工学院，河北 廊坊 065201）

平面杆件体系可以分为几何不变体系和几何可变体系。在工程应用中，只有几何不变体系才可以作为结构使用。其中，无多余约束的几何不变体系为静定结构，其内力通过静力平衡条件就可以唯一确定。有多余约束的几何不变体系为超静定结构，其内力确定需要在静力平衡条件的基础上补充变形协调条件。求解超静定结构内力时，力法是最基本、最经典的方法之一。而一次超静定梁是最基础的超静定结构，因此，用力法计算一次超静定梁的内力是结构力学学习过程中必须要熟练掌握的一项技能，也是最基本的技能。

1 一次超静定梁

梁是平面杆件结构中常用的一种类型。梁在竖向荷载作用下，截面产生的内力有剪力和弯矩，以弯矩为主，所以梁是一种受弯构件。一次超静定梁是指有一个多余约束的梁结构。常见的一次超静定梁有两类形式。第一类是两端铰支，中部有一个链杆支撑的多跨梁，如图1所示；第二类是一端固定另一端铰支的单跨梁，如图2所示。

图1 第一类一次超静定梁

图2 第二类一次超静定梁

2 力法解题的基本步骤

用力法求解超静定结构可以归纳为以下步骤：

a.确定超静定次数，撤出结构中的多余约束，用基本未知力代替，这样就将超静定结构转化为静定结构。原结构解除多余约束并去掉荷载得到的静定结构就是基本结构。将结构所承受的外荷载和基本未知力全部作用在基本结构上得到的就是基本体系。

b.依据基本体系与原结构在变形上应当一致的原则，补充变形协调条件，列出力法基本方程。一次超静定结构的力法基本方程为：δ11X1+Δ1P=0。

c.求解力法基本方程的系数项和自由项。计算梁的位移时，只考虑弯曲变形对位移的影响，忽略轴向变形和剪切变形对位移的影响。因此，在求解梁的系数项和自由项时，首先做出基本结构当基本未知力等于一时的弯矩图即单位荷载弯矩图，及外荷载作用时的弯矩图即荷载弯矩图。然后将单位荷载弯矩图图乘得到系数项，将单位荷载弯矩图和荷载弯矩图图乘得到自由项。一次超静定结构的系数项和自由项分别为：

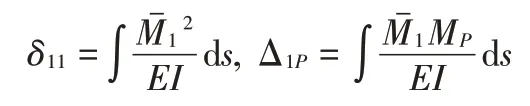
d.解力法基本方程，求出基本未知力的数值。一次超静定结构基本未知力的求解公式为

e.利用叠加法绘制超静定结构的弯矩图。对于一次超静定梁来讲

3 力法基本体系的选取原则

从力法解题的基本步骤中可以看出力法基本体系的确定是力法计算的基础。合理选择力法基本体系不仅能保证力法求解的准确性，而且有利于提高计算的效率。

力法基本体系的选取原则如下：

a.只能解除原结构中的多余约束，不能解除必要约束。用力法计算超静定结构的基本思路就是将超静定结构求解转化为静定结构求解，如果解除了必要约束，此时体系就变为几何可变，不再能使用力法求解。

b.只能从原结构中解除约束，不能增加约束。新增约束的出现会使基本体系与原结构的位移不能保持一致，满足不了基本体系与原结构在变形上应当一致的原则。

c.选择容易计算内力的基本体系。同一超静定结构可能存在多个力法基本体系的选取方式，合理的选取基本体系，可以减少图乘时的叠加，进而减少计算工作量。

4 常见一次超静定梁力法基本体系的选取

4.1 第一类一次超静定梁力法基本体系的选取

对于第一类这种两端铰支、中部有一个链杆支撑的多跨梁基本体系的常用选取方式有两种：第一种是将中部组合结点转化为铰结点并在铰结点处加一组集中力偶，第二种是撤掉中部支座链杆以集中力代替。

力法计算超静定结构时主要的计算量集中在系数项和自由项的计算上，为了便于比较两种基本体系，下面以右跨跨中布置一个集中力P 为例分别来计算这两种基本体系的系数项和自由项。

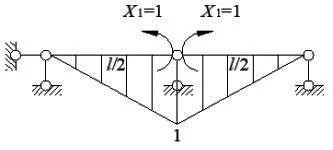
图3 图

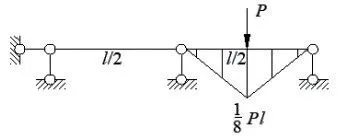
图4 MP图

系数项等于单位荷载弯矩图自身图乘。此时单位荷载弯矩图在l/2 处出现折点，用图乘法计算系数项时，需要分段进行图乘，弯矩图左右两跨对称，算出一侧乘2即可，最终图乘结果如下：

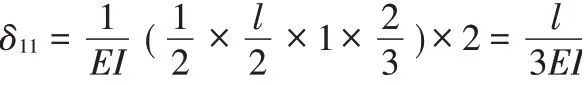
自由项等于单位荷载弯矩图和荷载弯矩图进行图乘。此时MP图只有右跨出现弯矩，用图乘法计算系数项时，只需将右跨的单位荷载弯矩图和荷载弯矩图进行图乘。图乘时MP图取A，Mˉ1图取yc，图乘结果如下：

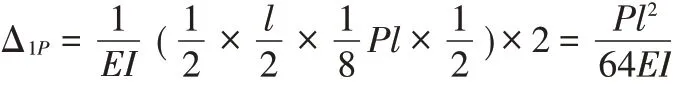
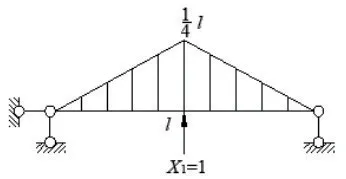
图5 图

此时单位荷载弯矩图在l/2 处出现折点，且弯矩图左右对称，因此用图乘法计算系数项时，算出一侧乘2 即可，最终图乘结果如下：

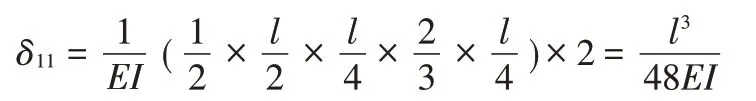
自由项计算时，由于单位荷载弯矩图和弯矩图均出现折点，所以需要分段进行图乘。根据图形特点，图乘时MP图取A，图取yc，分为四部分进行图乘，最终图乘结果如下：

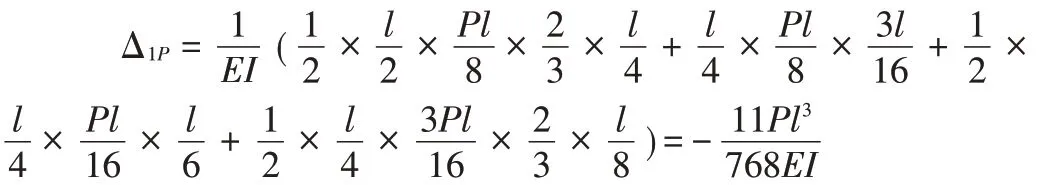
通过对比发现，第一类一次超静定梁在简单荷载作用下，使用图乘法计算两种基本体系的系数项和自由项时，第二种基本体系的计算工作量是第一种基本体系的几倍。如果原结构承受的是较为复杂的荷载，那两者的计算工作量差别会更大。因此，第一类超静定梁在基本体系选取时宜选用将组合结点转化为铰结点并在铰结点处加一组集中力偶的方法。

4.2 第二类一次超静定梁力法基本体系的选取

对于第二类这种一端固定另一端铰支的单跨梁基本体系的常用选取方式也有两种：第一种是将固定支座转化为固定铰支座并在固定铰支座处添加一个集中力偶，第二种是撤掉活动铰支座以集中力代替。

下面以满跨布置均布荷载q为例分别来计算这两种基本体系的系数项和自由项。

此时，系数项等于长度为l、高度为1 的三角形自身进行图乘，图乘结果如下：

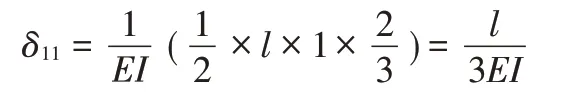
自由项等于三角形和二次抛物线进行图乘。图乘时MP图取A，二次抛物线的面积为2lh/3，图取yc，yc位于l/2处，图乘结果如下：

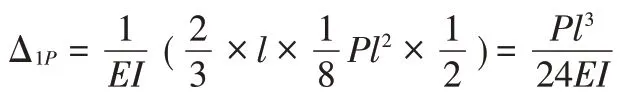
此时，系数项等于长度为l、高度为l 的三角形自身进行图乘，图乘结果如下：

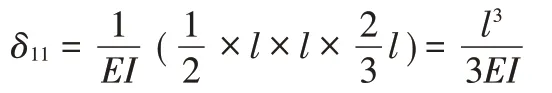
自由项等于三角形和二次抛物线进行图乘。图乘时MP图取A，此二次抛物线的面积为lh/3，图取yc，yc位于距离左端点1/4处，图乘结果如下：

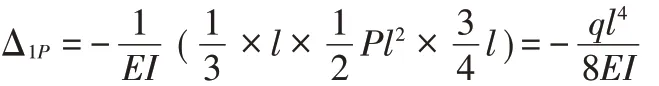
通过对比发现，第二类一次超静定梁两种基本体系在系数项和自由项计算上并无太大工作量差别。故使用力法进行此类梁计算时，基本体系选取以上两种均可。

5 结论

用力法进行超静定结构的计算，有三个重要的环节：力法的基本未知量、力法的基本体系、力法的基本方程。而力法的基本体系是这三个“基本”的核心，它直接影响着力法计算的准确性及难易程度。

通过对以上两种常见一次超静定梁力法基本方程中系数项和自由项计算对比，可以发现：力法基本体系选取时有多种方式，不同的方式会产生不一样的计算工作量，所以在力法基本体系选取时，在满足前两条选取原则的前提下，必须充分重视第三条原则，即选择容易计算内力的基本体系。对于常见的一次超静定梁在力法基本体系选取时，应尽量解除组合结点中传递弯矩的内约束，保证各杆间的弯矩不互相影响，进而达到简化图乘计算的目的。