基于灰色系统理论对山生柳生长量的分析预测

袁莹，李强峰，马成侠

(青海大学农牧学院农林系，青海 西宁 810016)

山生柳(Salixoritrepha)目前仅在我国有分布[1]，常生长于阴坡山地或沟谷地带，具有防止水土流失和涵养水源的作用[2].山生柳还有一定的药用价值，可用于镇痛、增强免疫力等[3].青海省位处青藏高原，自然环境较为恶劣，高寒地区的植物资源并不丰富.而山生柳适应性强，在青海省分布极广，常生于阴坡与半阴坡灌木丛中，是青海高山灌丛的主要建群种，此外，在放牧地区，山生柳的幼叶为牲畜喜食，枝条可供编织，树皮可提制烤胶，具有十分重要的经济意义[4].

目前，国内对于山生柳的研究多集中于遗传基因[5]、群落特征[6]或生物量[7]等方面，鲜见对其生长量方面的研究报道.生长量反映了植株的生长状况和生长潜力，对山生柳新梢生长量进行分析预测，有利于确定其生长的最适条件，还可作为山生柳栽培和抚育工作的理论依据，使其生态经济价值更好地被利用.

灰色系统理论针对的是在贫信息情况下的数据处理[8]，被广泛应用于工业[9]、农业[10]、经济[11]等领域.在农林业上，大量数据的获取一般也意味着大量人力和时间的投入，因此，合理应用能够对小样本数据进行有效分析的灰色系统理论，对于农林工作是十分有意义的.此前，在对林木的生长研究方面，贾宏炎等应用了灰色理论来确定各气象因子对林分生长的影响程度[12]；在对林木空间结构的预测中，李际平等对各个指标分别建立了灰色模型[13]，预测效果良好，但仅应用了传统的单变量等间距GM(1,1)模型，并未对非等距数据序列及多因素影响关系进行进一步研究.

本文以青海省不同地区的山生柳灌木林为研究对象，应用了灰色关联分析法和针对多变量数据序列的OBGM(1,n)的模型，提出以插值法将非等距序列等距化的方法，对灌木林地的立地质量进行综合评价，对影响山生柳生长的主要立地因子进行分析，再以立地条件为因子，综合考虑株高、冠幅、地径的影响，对山生柳新梢生长量进行合理预测，为高海拔地区山生柳造林工作提供了指导.

1 材料与方法

1.1 研究区域概况

研究区选取在青海省大通县、祁连县、平安区、天峻县和班玛县，地形地貌复杂多样，区域气候均为高原大陆性气候，具有年降水量少，气温日、年较差均较大的特征.大通县位于河湟谷地，平均海拔为2 720 m，年均气温4.9 ℃，年降水量523.3 mm；祁连县位于祁连山中段，平均海拔为3 169 m，年均气温1 ℃，年降水量420 mm；平安区地形复杂，平均海拔2 066 m以上，年均气温7.6 ℃，年降水量310.1 mm；天峻县位于柴达木盆地，平均海拔4 000 m以上，年均气温-1.5 ℃，年降水量360 mm；班玛县平均海拔4 000 m以上，年均气温2.4 ℃，年降水量638.4 mm.主要土壤类型为栗钙土、黑钙土、灰褐土、高山灌丛草甸土等[14]，主要植被类型为山生柳、鬼箭锦鸡儿、金露梅等.

1.2 研究方法

1.2.1 样地设置与调查 在大通县、祁连县、平安区、天峻县、班玛县，共设置33个样地，使用GPS工具记录样地点坐标和海拔，具体情况见表1.样地规格均为20 m×20 m，使用钢卷尺、游标卡尺等工具对样地内所有山生柳灌丛进行株高、冠幅、地径、新梢生长量的测定，使用取土器采集0～10 cm土层的土壤样品，并测定土层厚度.

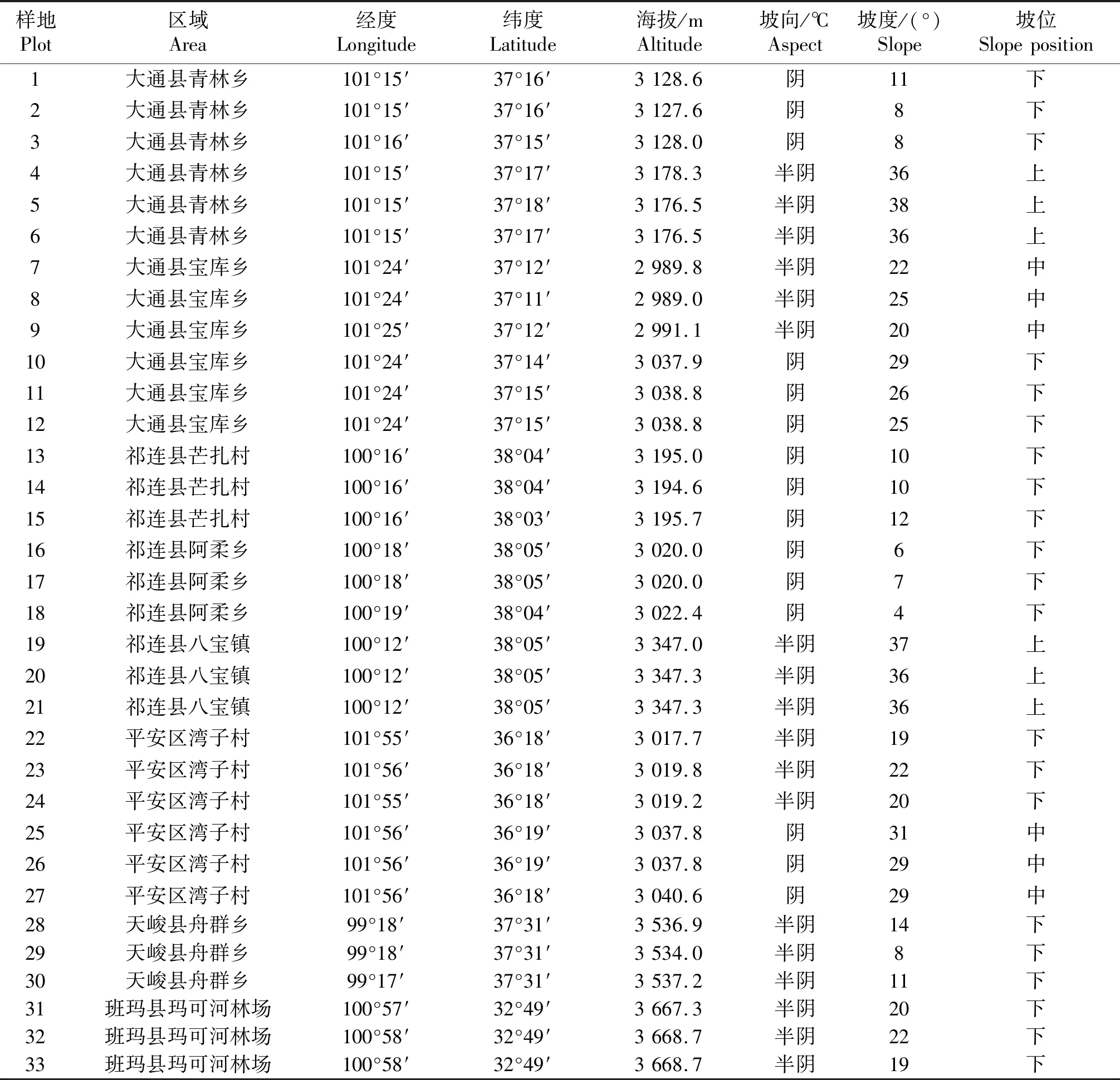
表1 样地位置Table 1 Location of sample plot

1.2.2 土壤养分测定 土壤的理化性质十分复杂，不同区域的土壤间养分含量也有不小的差异，土壤质量对植物的生长也起着不小的作用[15].测定的土壤指标及相应的测定方法如下：采用重铬酸钾容量法(水合热法)测定土壤有机质，采用半微量开氏法定全氮，采用硫酸高氯酸消煮法测定全磷，采用氢氟酸消解法对全钾进行测定，采用EDTA容量法测定全镁，采用EDTA容量法测定全钙，采用碱解扩散法测定碱解氮，采用0.5 mol碳酸氢钠浸提(钼锑抗比色法)测定有效磷，采用1N中性醋酸铵浸提(火焰光度计法)测定速效磷，中性盐溶液浸提后，使用酸度计测定pH[16-18].各样地的土壤测定情况见表2.

表2 各样地土壤养分状况及变异系数Table 2 Soil nutrient status and coefficient of variation in various fields

1.2.3 分析方法

1.2.3.1 立地质量评价 立地条件作为影响灌丛生长的十分重要的因子，一直以来也是国内外学者的研究重点.此前已有学者利用数量化理论和灰色关联分析法对立地条件进行综合评价[19-20].以优势木株高为反映立地质量的参照序列，计算各因子的关联度从而确定权重，最后根据等级划分情况进行赋分，经过加权计算即可得到各样地的立地得分.得分高，则表明立地质量好.为避免绝对数值带来较大误差，计算前需将参照序列数据归一化.相关公式如下：

1)归一化处理：

(1)

式中：yi为第i块样地数值，y为所有样地的平均数值，xi为归一化处理后的数值.

2)灰色关联度计算：

ξj(k)=

(2)

(3)

式中：rj为第j个因子的灰色关联度，其中m为因子总数；ξj为k时刻的关联系数，ρ为分辨系数.

3)权重计算：

(4)

式中：Wj为第j个因子的权重，为百分数形式.

4)得分计算：

(5)

式中：T为总分，范围为0～10分；Sj为第j个因子的评分值.

1.2.3.2 非等间距多变量预测模型 对于非等距的灰色预测模型也有多种建模方法，此前尹晖等对这些建模方法进行了分类对比分析，得出等距处理建模效果优于赋权处理的结论[21].此外，翟军等将提出的MGM(1,n)模型与传统GM(1,1)模型进行对比[22]，发现多变量模型的拟合效果更优.本文采用的即为基于等距处理的非等间距多变量灰色预测模型.具体的建模方法如下：

1)等距处理：令Y(0)={Y(0)(t1)，Y(0)(t2)，…，Y(0)(tm)}为非等间距序列，其中间距Δti=ti-ti-1，Δti不为常数.采用最常用的三次样条插值法来进行数据的初步处理.令等距化后的序列为X(0)={X(0)(1)，X(0)(2)，…，X(0)(k)}.

2)OBGM(1,n)模型：根据曾波等对各种实用灰色预测模型的分析对比研究[23]，本文选用基于粒子群算法优化背景值的OBGM(1,n)模型，该模型相较于传统的MGM(1,n)模型，提高了模型的收敛能力及速度，弥补了传统多变量模型在兼容性和适应性上的不足，关于背景值优化的具体过程本文不再赘述.

建立多变量预测模型，令X1(0)为因变量序列，Xi(0)(i=1,2,3,…,n)为相关变量序列，Xi(1)为Xi(0)的一次累加生成序列，Zi(1)为Zi(0)的紧邻均值生成序列.模型应用的差分模型为：

(6)

式中：ξ为最优背景值系数.根据最小二乘法进行参数估计，推导得到时间响应函数为：

(7)

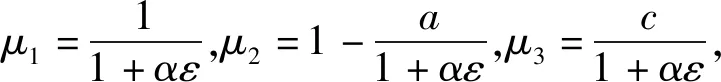
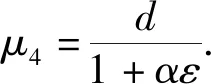
(8)

1.2.3.3 模型检验 模型建立后必须在相应的精度检验中显示合格才能在实际生活中应用.本文采用的模型检验方法是相对误差检验法和后验差检验.在相对误差检验法中，需计算模型的残差和平均相对误差，一般认为残差及平均相对误差小，模型精度高，反之则表明模型精度低.在后验差检验法中，需计算得到模型的后验差比和小误差概率，后验差比越小则表明模型精度越高，而小误差概率越小则表明模型精度越低.

2 结果与分析

2.1 新梢生长量及相关指标

新梢生长量是能够直观反映树势强弱的指标，目前也有不少学者应用以新梢生长量为指标的研究方法，判断植株的生长状况及生长适宜条件[24-26].立地条件作为影响山生柳生长的决定性因素，分析各立地因子对生长量的影响，能够为之后的造林工作提供数据基础.此外，山生柳的其他生长指标对新梢生长量同样有着或多或少的影响，如株高、冠幅和地径，因此在建立预测模型时，应综合考虑这些生长指标的影响.表3为试验地生长量及相关指标的数据统计情况.

表3 新梢生长量及相关指标Table 3 Shoot growth and related indexes

2.2 立地评价

2.2.1 立地因子分级 为了更加全面、更加准确、更加方便地对立地质量进行评价，从海拔、坡向、坡度、坡位、土壤条件这6个方面进行综合分析.为了在能较为全面地反映土壤之间差异的前提下减少数据噪声，选取差异较大的几组土壤养分指标进行分析.根据表2，可知样地土壤间差异较大的为速效钾、有机质、全氮、有效磷，因此，确定这4个指标及海拔、坡向、坡度、坡位、土层厚度为评价立地质量的主要立地因子.对各因子划分等级，见表4.

表4 立地因子等级划分Table 4 Classification of site factors

2.2.2 立地质量评分 根据表4的分级结果，等级一、二、三相应为0、0.5、1分，对样地的此九个立地因子进行赋分统计，作为关联分析的比较序列.此外，将样方内山生柳优势株的平均株高归一化，作为能够反映立地条件优劣的参照序列.经过整理得到的各样方立地因子情况见表5.

表5 归一化数据Table 5 Normalized data

样地Plot参照序列Referencesequence海拔Altitude坡向Aspect坡度Slope坡位Slopeposition土层厚度Soilthickness全氮Totalnitrogen有机质Organicmatter有效磷Availablephosphorus速效钾Availablepotassium11.24111110.50.50.5021.23111110.50.50.5031.33111110.50.50.5040.9510.5000.5000.50续表5 Continuedtable5样地Plot参照序列Referencesequence海拔Altitude坡向Aspect坡度Slope坡位Slopeposition土层厚度Soilthickness全氮Totalnitrogen有机质Organicmatter有效磷Availablephosphorus速效钾Availablepotassium50.8310.5000.5000.5060.8410.5000.5000.5071.0410.50.50.510.50.500.581.1010.50.50.510.50.500.591.1310.50.50.510.50.500.5100.83110.510.50.50.500110.77110.510.50.50.500120.89110.510.50.50.500131.31111110.50.510141.40111110.50.510151.26111110.50.510161.37111111111171.31111111111181.42111111111190.800.50.5000.5110.50200.720.50.5000.5110.50210.690.50.5000.5110.50220.7110.50.5110000230.9710.50.5110000240.7810.50.5110000250.93110.50.510.00.00.00.0260.83110.50.510.00.00.00.0271.00110.50.510.00.00.00.0281.0100.51100.50.50.00.0291.0000.51100.50.50.00.0301.0900.51100.50.50.00.0310.7200.50.5101.00.50.50.5320.7100.50.5101.00.50.50.5330.7900.50.5101.00.50.50.5

使用Matlab软件对以上数据进行灰色关联分析计算，得到海拔、坡向、坡度、坡位、土层厚度、全氮、有机质、有效磷和速效钾的关联度分别为0.73、0.71、0.66、0.68、0.70、0.57、0.57、0.56、0.49，计算得到其权重分别为12.9%、12.5%、11.7%、12.1%、12.3%、10.0%、10.0%、9.9%、8.6%.

山生柳优势株平均高既能够反映林地质量条件，也能够代表植株的生长状况，因此在综合分析了九个立地因子后，可得出结论：对样地质量及山生柳生长影响最大的因子为海拔，影响最小的因子为速效钾含量.最后，根据所获得的各因子权重可计算得到所有样地的立地得分.

2.3 生长量预测

2.3.1 数据序列等距化结果 整理所获得的各样地评分结果，采取插值法进行等距化，获得的等距序列再进行下一步分析.将具有相同得分的山生柳样地进行综合处理，计算得到所有观测值的平均值.令生长量、株高、冠幅、地径这四个指标作为预测模型的原始数据序列，其中生长量为需进行预测的自变量序列，株高、冠幅和地径则作为相关因素序列.等距化后的数据序列见表6.

表6 数据序列Table 6 Data series

2.3.2 预测模型构建 根据表5构建相应的OBGM(1,4)模型.将所构建的预测模型与Logistic模型和GM(1,1)模型进行对比，以平均相对误差(MRE)和残差平方和(SSE)为衡量指标，能够更加全面地表现模型预测效果的优劣.3种模型的预测结果见表7.由于在建立灰色模型时，第1行数据仅为参照数据无误差，因此不加入对比.

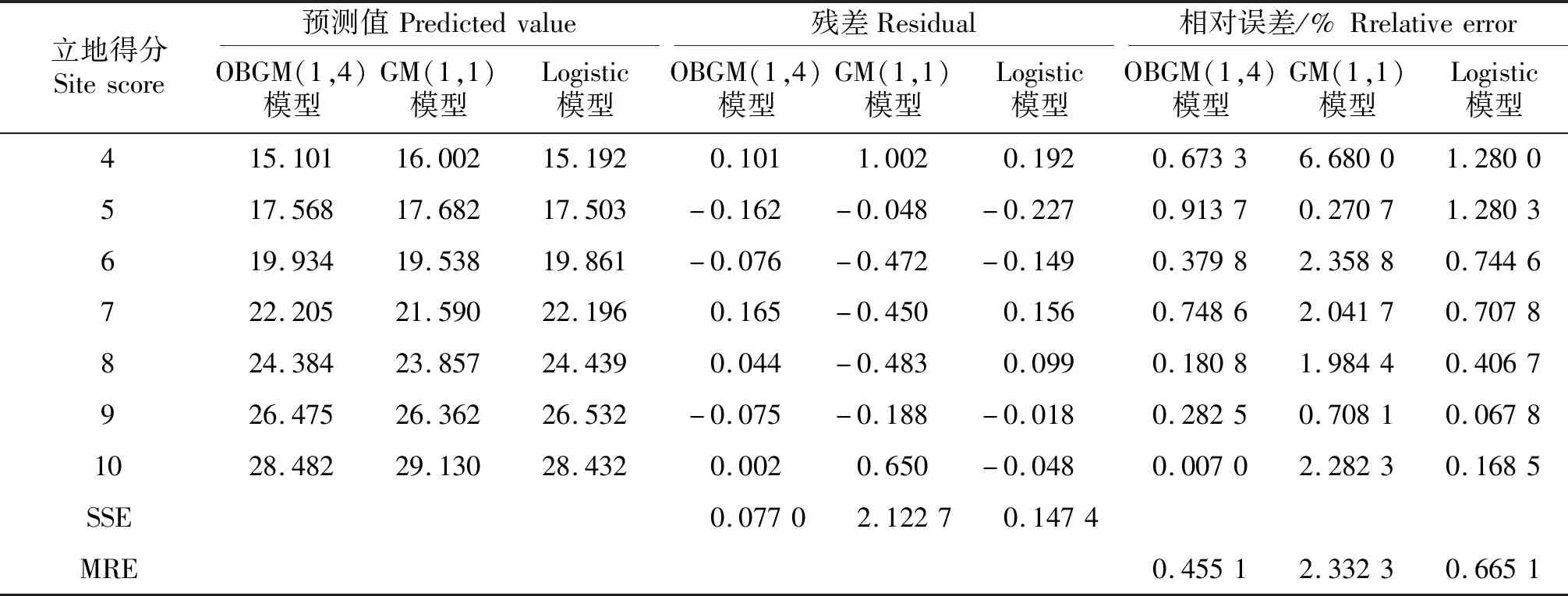
表7 三种模型的预测结果及对比Table 7 Prediction results and comparison of three models

根据表8中SSE和MRE的结果对比可知3种模型精度高低为：OBGM(1,4)模型>Logistic模型>GM(1,1)模型，可以初步判断OBGM模型的拟合效果最优.最后，为确定残差有无异方差性，对OBGM模型的残差进行White检验，检验结果如下：

表8 White检验结果Table 8 The result of White Test

由于F-statistic和Obs*R-squared的P值分别为0.805 1和0.698 0，远大于0.1，预测模型的残差项无异方差现象.此外，模型的平均相对误差仅为0.455 1%，通过相对误差检验可判断此模型精度较好；计算得到此模型的后验差比和小误差概率分别为0.02和1，经过后验差检验法也可确定模型精度等级为好.因此，综合考虑了多变量影响的OBGM(1,4)模型可以实际应用，且取得了十分良好的预测效果，模型精度略优于另两种模型.

3 讨论

不同的立地条件下植被的生长表现也有所差异[27]，影响植物生长的立地因子中，海拔、坡向、坡位、坡度、土壤条件等一直被作为研究的重点[28-29].一般来说，随着海拔发生变化，温度、水分条件等也会随之发生变化，从而限制植物的生长[30]，土壤养分作为反映土壤肥力的重要指标，是植被生长发育主要限制因子[31].有研究表明：在影响山生柳生物量的立地因子中海拔是最为关键的，随着海拔的升高山生柳灌丛的生物量受到明显限制[32].本研究对海拔、坡向、土层厚度、土壤有机质等九个立地因子进行了灰色关联分析，结果表明各个因子对山生柳生长的影响程度大小为：海拔>坡向>土层厚度>坡位>坡度>有机质>全氮>有效磷>速效钾，其中海拔的影响权重为12.9%，速效钾仅占8.6%.因此，在对山生柳进行栽培或抚育工作时，应首先考虑海拔、坡向、土层厚度这几个因素，结合评分的方法也能对各个地区的立地质量进行简单的等级划分，便于造林工作的规划.

以立地条件为主要因子，建立植被的生长量预测模型，能够直观地反映不同立地下植被的生长潜力.目前国内外关于植物生长预测模型方面的研究报道有不少，其中Logistic模型因具有饱和增长特征而常被研究者们使用[33]，并且此前也有学者将同样基于灰色系统理论的GM(1,1)模型应用于植物生长的预测[34]，但这些传统的模型建立方法均未能考虑到一些受立地影响的相关变量对植株生长量的作用.本文在确定了各样地的立地质量得分后，除新梢生长量外，引入了株高、冠幅、地径作为相关因素，建立了OBGM(1,4)模型对生长量进行预测，并将其与Logistic模型和GM(1,1)模型进行对比.研究结果表明：3种模型的预测效果对比结果为：OBGM(1,4)模型>Logistic模型>GM模型.因此，在对山生柳生长量的预测中，非等距OBGM模型表现良好.结合上诉立地评分的方法，应用该模型对山生柳灌丛的新梢生长量进行预测，能够有效反映出山生柳灌木林地未来短期内的生长状况，对于山生柳的选优工作有所助益，为之后林地的经营培育提供合理的指导和标准.

4 结论

本文对不同地区的山生柳灌木林进行研究，通过灰色关联分析法确定各立地因子的权重，并对立地质量做出综合评价，再以此为基础建立非等距多变量灰色模型.模型考虑了多个指标的影响，对山生柳的生长量做出合理预测.研究结果表明，在海拔、坡向、坡度、坡位、土层厚度、全氮、有机质、有效磷和速效钾这九个立地因子中，对山生柳林地质量及山生柳生长状况影响最大的为海拔，其次为坡向和土层厚度，影响最小的因子为速效钾；在对山生柳生长量的预测中，加入了株高、冠幅、地径作为相关因素进行分析的多变量OBGM(1,4)模型拟合效果要略优于传统的Logistic模型和GM(1,1)模型.