高中数学解题教学中探究性学习策略研究
李 敏
(新疆第五师双河市83团第一中学 833303)
新课程改革明确指出:高中数学教学需致力于发展学生的创新意识并促使学生创新知识探究及数学解题等综合能力的有效发展.对此,为保证理想的教学效果,教师在教学过程中当谨遵新课程改革之号召,并对传统教育模式予以有效改革,有助于发展学生的数学综合能力,并为学生今后的学习奠定牢固基础.
一、教给学生探路的方法,让学生探究更科学
针对解题思路的探究,其过程也便是对问题的识别、假设及验证,而就上述过程而言,首要之务便是明确识别对象,即问题的具体归属.通过对问题所属类型的探知,便可运用相应的解题方法去求得问题的答案.而就高中生而言,虽大多数高中生已经积累了较为丰富的解题经验,且理性思维亦得到了极大程度的发展,但其头脑中仍难免会存在部分说不清、道不明的解题意识.至此,若教师能及时引导学生探索解题思路的方法,则势必能帮助学生减少其在自主探索时的盲目性.依照波利亚所提出的解题思想,探究解题思路的思索阶段主要包含三大步骤,分别为审题、联想及探路.当然,针对解题思索的三大阶段,不同阶段所对应的目的亦不尽相同.如审题的核心目的主要有二:分别是明确问题的已知条件及要求和能否换一种语言叙述方式来表达题意;而联想环节的目标则包含两方面:一是确认题目属于何种类型以及该类型的题目通常有多少种解法;二是根据题目能联系到那部分知识,解题过程该如何运用此部分知识以及是否能对问题予以进一步的转化.至于探路阶段的核心目的主要有三:一是能否把已知转化为可知,未知转化需知;二是否遇到过同一类型的问题,在解决同类型问题时运用了怎样的方法与思路,是否能为解决此问题提供借鉴;三是何症结导致转化难以实现?
对于上述三大步骤,其均是为了明确学生的解题思路,而学生解题思路一旦明确,其之后的探究过程势必也会变得更加有效且科学.
二、借题引发再次探究,扩大探究的成效
诸多高中数学解题教学课堂,教师仅是一股脑地向学生抛出多道问题,且问题之间毫无关联.如此一来,因学生将同时检阅多个问题场景,故将导致其阅读理解的负担增加,继而也将使得大量宝贵时间被无端浪费.不仅如此,过于分散的问题亦无法帮助学生建构出系统的方法体系,更遑论促使学生思维的深度发展.对此,教师需基于问题的依托来对其辐射及教学功能予以充分发挥,方能在扩充学生的思维容量同时锤炼学生思维品质的深广度.
三、引导学生一题多解,培养思维灵活性
教师于实际教学中需想方设法帮助学生突破定式思维的限制,继而积极引导学生多角度展开思考,以此另辟蹊径式的帮助学生解决问题,有助于促进学生想象、思考、探索等数学综合能力的有效发展.
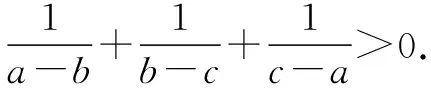
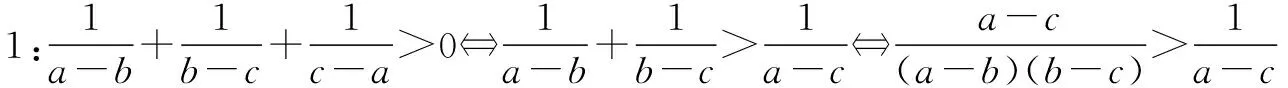
∵a>b>c>0,∴a-c>a-b>0,a-c>b-c>0,
证2:∵a>b>c>0,∴a-b>0,a-c>b-c.
针对同一道题目,若从不同的角度切入,则所得启示也不尽相同.当然,高中数学解题教学采用此种方式并非是要探究多种解法,而是要借助一题多解来锻炼学生的知识综合运用能力,以此方能锻炼学生思维,并促使学生思维灵活性及深刻性的有效发展.
四、采取探究式解题教学,培养学生创新思维
函数既是高中数学的教学重点,也是初中函数知识的延伸与拓展.而众所周知,函数所考察的核心内容在于学生对问题的理解程度以及对知识的实际应用能力.对此,若教师仍是以按部就班的方式来展开教学,势必难以满足学生的学习需求.故教师需秉持创新的思路来帮助学生突破原本解题思路的禁锢,以此方能帮助学生在发现新的问题解答方法同时促使学生解题能力的有效提升.
比如例题:直线AB:y-ax=1与双曲线M:2x2-y2=1有两个相交点,分别为点C与点D,求a的取值范围.对于例题,学生基于过往的学习经验很容易便能得出题目的解法:即通过对直线与双曲线方程的联立整理便可得出方程式(a2-2)x2+2ax+2=0.通过Δ>0可求出a的取值范围.对于上述较为常规的解法,教师便可以此为基础来予以拓展及延伸,诸如首先要求学生预测结果,而后借由画图的方式来加以验证,学生经过再次讨论对解题思路进行改进:a2-2≠2,通过引导学生一道题应用多种解题思路,让学生在解题过程中打破思维定势,从多角度地观察和分析问题,采用不同的思路对问题进行解决,能够增进学生对函数的了解,为其今后的学习奠定牢固基础.
总之,高中数学解题教学,教师需将教学的重点放在解题思路、方法与技巧的讲解之中,以此方能促使学生逐步形成良好的数学思想及素养.与此同时,考虑到高中数学解题教学原本对学生理解知识和掌握解题能力等各方面均有较高要求,故为保证理想的教学效力,教师还需将变式训练的理念引进高中数学解题教学,以此方能在顺应教育改革要求同时让学生深刻体会学习数学的乐趣,最终实现提升教学效果和提高学习成绩的目的.

