环境激励下港口起重机结构模态参数识别实验研究
杨 凯 黄金晶 王嘉卿
上海海事大学工程训练中心 上海 201306
0 引言
模态参数对港口起重机的结构设计,特别是港口起重机结构的减振、抗振设计具有非常重要的指导意义。传统模态测试方法激励起港口起重机大型结构较困难,且激励很难测量,在得到准确输入与输出方面有很大局限性,已成为港口起重机发展的障碍。在港口起重机领域,使用时域信号准确识别其结构的模态参数是迫切需要解决的问题。大型港口起重机的结构复杂,所需测点数较多,对采集仪通道数和传感器数量的要求较大,测试难度大,成本高,这也是当今大型港口起重机测试的一项难点。
使用扩展的随机减量技术与ITD法相结合的RDT/ITD结合法识别环境激励下港口起重机结构的模态参数,使用运行状态模态分析技术(OMA),识别大型港口起重机结构的模态参数,以克服传统模态测试方法的不足。运用移动测点法进行试验,以少量的传感器以及有限的通道数测试大型港口起重机主梁结构的振动信号,这种方法为解决通道数和传感器不足提供一个实例依据。
1 工况描述及有限元分析
1.1 工况描述
以JAJ-15t-37.25mA4型岸边集装箱起重机为研究对象,在自然环境下(地处海边,有较明显的风载荷激励)进行实验模态分析。该机起升高度为23.0 m,工作级别为A4,主梁形式为桁架双主梁,单小车形式。
1.2 有限元分析
整机有限元模型如图1所示。利用Ansys建立港口起重机模型,并使用模态分析模块进行模态分析,得到模态分析结果。前五阶固有频率及振型描述见表1。

图1 整机有限元模型

表1 大梁不同阶次的振型描述
2 扩展RDT/ITD港机模态识别
2.1 试验方案
港口起重机模态试验采用频率范围为0.17~100 Hz的941B超低频拾振器,采用INV3062C数据采集仪采集起重机振动信号,用DASP分析软件进行信号分析。
港口起重机大梁结构总长共85.30 m,对其进行7等分得到共8个截面的16个测点,如图2所示。由于起重机主梁纵向影响较小,可暂不考虑,只考虑垂向和横向,共4×8=32测量通道数,同一截面的2个测点都要考虑2个方向,主梁结构部分振型会存在扭转形式,同时测量同一截面2个测点可实际反映出主梁的扭转振型形式。

图2 港口起重机大梁结构测点布置
在实际测试中,经调试采集仪共7个通道数可用,具体方案为:确定一个固定参考点,使用7个低频拾振器,在16个拟定的测点,分别在起重机横向(X)和垂向(Y),在同一参考点下进行分批次移动测试。
为防止选取固定参考点时,所选参考点为结构的振型节点,故选取整个结构的前端点1(X)和1(Z)为每次移动测量试验的固定参考点,通过多次移动其他传感器来实现对起重机整体主梁模态的测试(见表2),每组试验的采样时间为1 800 s。
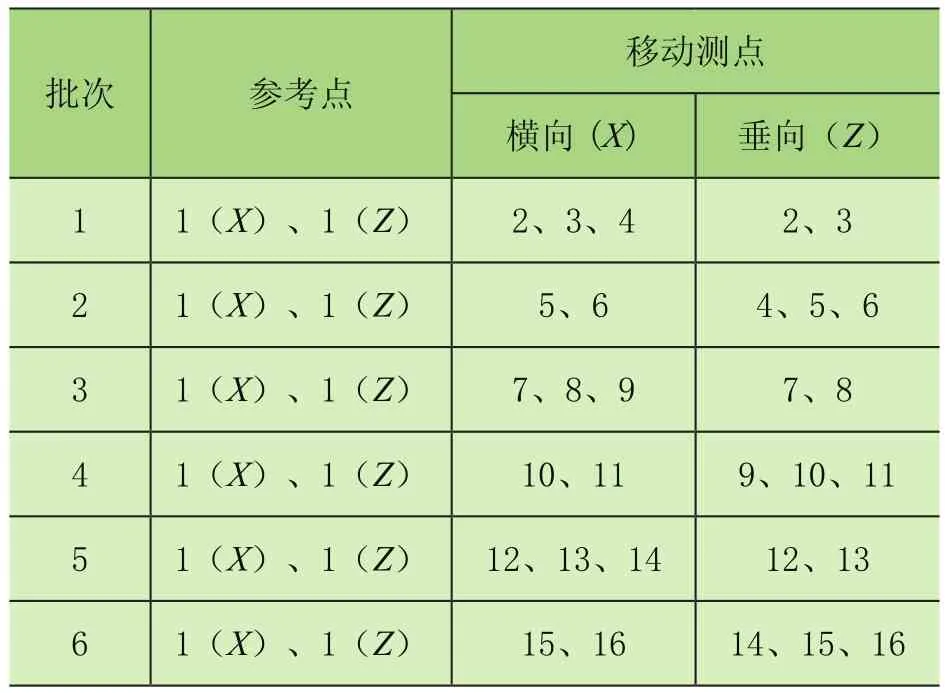
表2 主梁测试方案
1号测点(即固定参考点)低频拾振器安装情况如图3,低频拾振器采用磁钢吸附在测点位置,垂向的测试采用垂直类型的低频拾振器,横向的测试采用水平类型的低频拾振器。

图3 1号测点(固定参考点)低频拾振器安装情况
2.2 RDT/ITD模态参数识别
由于实验方案采用了移动测点法的测试方法,需要经过多批次进行测试采样,这就形成了多种工况下的测试信号,不同批次的振动信号外界条件不一样,却有相同的参考点。所以,在进行模态分析时,将不同工况下的振动信号分批次处理分析,然后基于参考点进行总结。将每一批次的测点相同方向的进行同时处理分析,即同一批次横向测点的信号处理分析一次,参考点为参考点横向的测试信号;同一批次的垂向测点信号处理分析一次,参考点为参考点垂向的测试信号。
按照上述分析方案,将实验所得各测点的时域波形信号输入Matlab中,用随机减量法程序进行分析处理,得到随机减量函数,即自由响应函数。图4是测点16随机减量法处理后得到的自由响应函数图像。

图4 测点16RDT处理后得到的自由响应函数
为检验随机减量处理后抽取的信号是否仍具有原信号的频谱特性,在此对原信号和随机减量处理后的信号做功率谱分析,测点16的信号随机减量处理前后功率谱如图5所示。

图5 信号随机减量处理前后功率谱
由图5可知,随机减量技术处理后的信号与原始信号的频谱峰值处于同一频率范围内,并未出现虚假频率。所以,随机减量信号保证的处理后信号的能量分布与原始信号一致,保留了原始信号的频谱特性。
通过对测点采取延时采样,可得到虚拟测点,构建响应矩阵,然后根据响应矩阵求解结构模态参数。ITD识别方法的拟合曲线与原始自由响应信号拟合图如图6所示。由图6可知,识别拟合效果较好,拟合曲线与原始信号比较并未出现遗漏拟合或虚假拟合。对不同批次的实验数据依次进行识别,得到表4所示模态频率识别结果。由表4可知,频率识别结果标准差较小,识别值得数据浮动不大,频率识别结果较可靠。港口起重机模态阻尼识别结果如表5所示。

图6 拟合曲线与原始自由响应信号拟合图

表4 港口起重机模态频率识别结果

表5 港口起重机模态阻尼识别结果
由表5可知,阻尼识别值的标准差也在允许范围内,与频率识别值得标准差相比,数据浮动稍大,数据在可接受范围内。
2.3 港机结构模态识别结果比较
除了考虑使用随机减量法对响应信号进行处理分析,然后再进行模态参数识别外,为比较识别结果的准确性,本文使用DASP V11模态分析软件,运用时域模态参数识别较为成熟的随机子空间法(SSI)以及poly-IIR法,同时对本实验所采集的数据进行了处理分析。这3种方法的模态参数识别结果见表6。
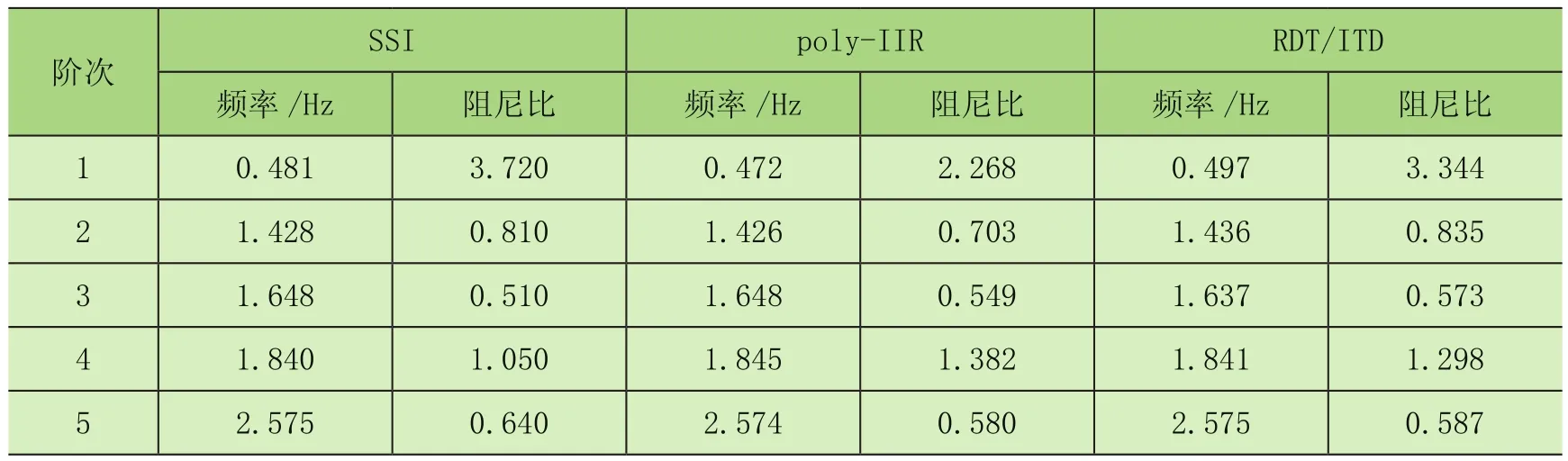
表6 各方法识别港及结构模态参数值
由表6可知,随机子空间法(SSI)、poly-IIR、RDT/ITD法所识别的模态频率值与有限元模型计算的理论值之间的误差都在10%以内,这3种识别方法所识别出的频率值相差不大,接近港机实体的真实模态值。
由表7可知,这3种方法频率值的识别结果相差不大,说明这3种方法所识别出的频率值基本吻合,RDT/ITD法识别出的频率值与SSI法、poly-IIR法一样有相当高的可信度。在阻尼识别方面,虽然吻合性不像频率值那么高,但具有相同的走势,且识别值处于一定范围内,尚可接受,仍有提升空间。

表7 有限元计算值与各方法结果比较分析
3 结论
1)利用RDT/ITD结合算法识别的港及结构的模态参数结果与SSI和poly-IIR法识别结果具有一致性。
2)利用RDT/ITD结合算法识别大型结构的模态参数具有可行性。
3)RDT/ITD结合识别法所识别的频率值可靠度很好,对于阻尼的识别还存在一定的误差。
本次实验也证明了使用移动测点法代替多测点同时测量在大型港口机械模态测试中的可行性。

