基于旋转变换的混沌光学图像加密方法

葛琳琳，姜文昊，张 威，李易霖

（1.辽宁石油化工大学，辽宁抚顺113001；2.大连海洋大学，辽宁大连116023）

近年来，光学图像加密技术在光学信息处理中显得尤为重要，它具有计算速度快、光学并行等优点，在信息安全系统中具有广泛的应用前景。目前已经提出了许多光学图像加密方法，例如利用傅里叶变换（FT）、分数傅里叶变换（FRT）和扩展FRT进行光学图像加密的方法[1]；利用傅里叶平面上的随机相位掩膜（RPM）的拼图变换（JT）以及加密图像的拼图变换对光学图像进行加密方法[1]；基于莫尔光栅、水印、偏振光、像素加扰、无透镜光学安全系统和二进制密钥编码的光学图像加密方法[2]；在傅里叶平面中，利用具有夹层扩散器的孔径，提出了二维图像光学加密中的复用方法[2]；还提出了基于Ikeda的非线性延迟动力学和光环谐振器的方法[3]，以及基于FRT的混沌的加密方法[1]。

基于混沌的加密方法已被用于光通信，混沌函数对初始条件非常敏感，在光学图像加密技术中，使用RPM对图像进行加密，并且必须将整个RPM发送到接收者一侧来对原始图像进行解密。因此，这些方法中的数据安全性变得很差[4⁃6]。

利用旋转变形（GT）对图像进行加密，并且使用混沌函数生成两个RPM，这些RPM被称为混沌随机相位掩膜（CRPM）。该方法中，输入图像在输入平面上乘以第一CRPM，然后在执行第一GT，将得到的输出图像乘以第二CRPM，然后在执行第二GT。处理后在GT平面上获得加密图像，利用Logistic映射、帐篷映射和Kaplan⁃Yorke映射三种混沌函数生成CRPM，并评估均方差（MSE），对所提方法在旋转角度和CRPM的种子方面盲解密的鲁棒性进行评估，并给出加密和解密技术的光学实现方案。

1 旋转变换

GT是一个线性正则积分变换，在相位空间的扭曲位置⁃空间频率平面(xi,qy)和(yi,qx)中产生旋转，带参数旋转角α的二维实函数f(xi,yi)的GT定义为[7⁃8]：

核函数为：

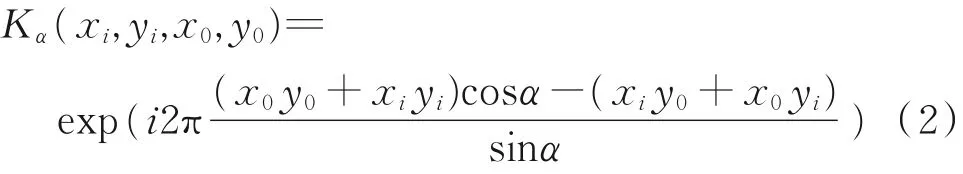
式中，(xi,yi)为输入平面坐标；(x0,y0)为输出平面坐标。

当在Diracδ函数δ(x0-xi)上执行GT时，得到式（2）中的旋转核函数作为输出函数，逆GT的旋转角对应于GT的相反数-α，定义为：

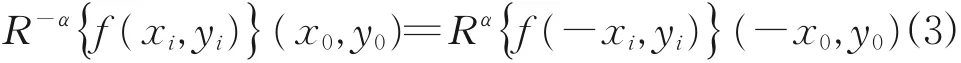
对于α=0，对应于恒等变换；对于α=π/2，以π/2的坐标旋转到正/逆FT；对于α=π，得到逆FT；对于α=3π/2，在π/2的坐标旋转的逆FT，对于旋转角度α的其他值，GT的核函数Kα(xi,yi,x0,y0)具有恒定幅度和双曲相位结构。对GT提出了两种类型的调整。第一种图像旋转是以特定角度在位置和动量平面一起旋转；第二种调整为交叉旋转，在(qx,py)和(qy,px)相空间中执行联合旋转。其中，qx和qy是位置坐标，px和py是动量坐标，GT和FRT的性质有一定的相似性，GT和FRT之间也存在基本差异，因为GT的核函数是双曲波和平面波的乘积，而FRT的核函数是球面波和平面波的乘积。

2 混沌函数

混沌函数用于描述非线性动力系统。混沌函数具有几个有趣的性质，对初始条件非常敏感，这使它在数据安全方法中非常重要。这些函数产生随机迭代值，随机迭代值在边界之间是有限的，迭代值的收敛性在任何迭代值之后都是不可见的[9⁃10]。

本文使用3个混沌函数，第1个混沌函数是Logistic映射，其定义为：

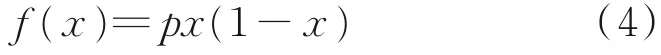
该函数为有界函数，即0＜p＜4，其迭代形式可以表示为：

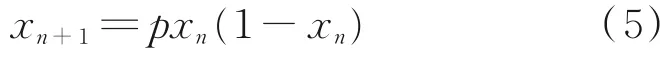
以x0为初始值（混沌函数的种子值）。第2个混沌函数帐篷映射定义为：

该函数是有界函数，即0＜a≤2，其迭代形式可表示为：

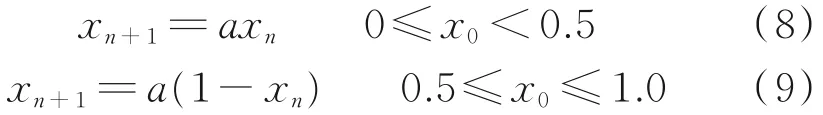
以x0为初始值。第3个混沌函数是Kaplan⁃Yorke映射，其定义为：

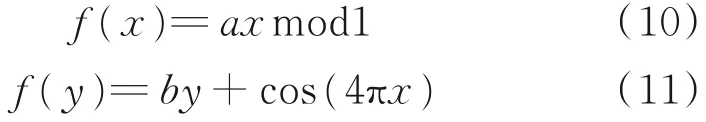
该函数也是有界函数，即0≤a≤2和0≤b≤1，其迭代形式可表示为：

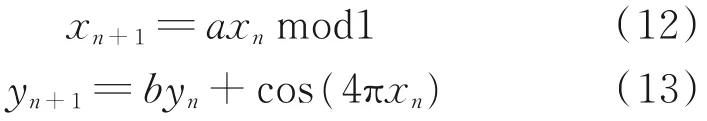
以x0为初始值，利用混沌函数生成RPM。Logistic映射和帐篷映射为一维混沌函数，Kaplan⁃Yorke映射为二维混沌函数。对于二维混沌函数，需要2个种子值来产生CRPM，CRPM具有普通PRM无法比拟的优点。在利用RPM的光学图像加密技术中，使用RPM对图像进行加密，并且必须将整个RPM发送到接收方来解密原始图像。因此，这些方法中数据的安全性变得更低，在使用CRPM的光学图像加密技术中，只有称为种子值的初始元素被发送到接收方一侧，而不是发送整个RPM。

3 提出的方法

所提出的加密和解密技术是基于GT和混沌理论，加密和解密过程如图1所示。

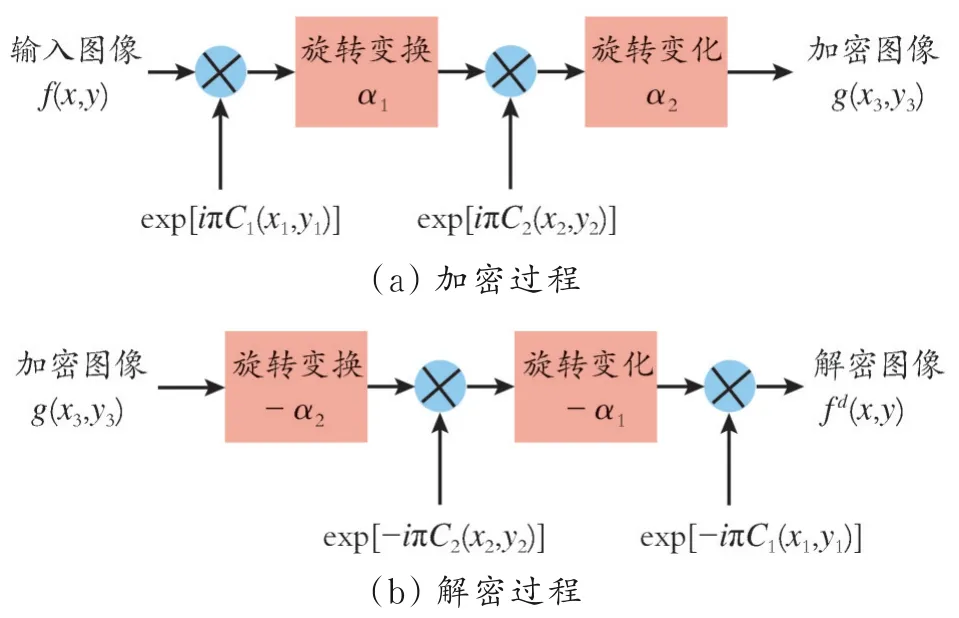
图1 加密和解密过程

执行2次GT，并在中间平面上引入利用混沌函数产生的RPM，旋转角作为图像加密和解密技术的密钥。设f(x,y)为要加密的原始图像，输入图像乘以由相位函数exp[iπC1(x,y)]表示的第1个CPRM，其中C1(x,y)是由混沌函数生成的随机数序列，旋转角α1的第1次GT操作通过式(14)得出：

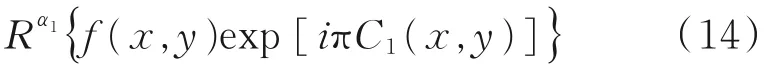
利用第2个CPRM对第1次GT操作的结果进行编码，第2个CPRM表示为相位函数exp[iπC2(x2,y2)]。其中，C2(x2,y2)是使用不同的种子值获得的第2个混沌函数，然后进入旋转角α2的第2次GT操作，在输出平面上的分布为：

g(x3,y3)=

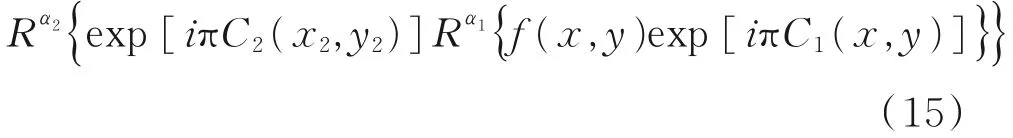
解密是加密的逆过程，在g(x3,y3)上执行第1个逆GT（GT旋转角度的相反数-α2），然后乘以第2个CRPM的共轭，在得到的输出上执行第2个逆GT，再乘以第1个CRPM的共轭，最后得到解密图像，解密过程表示为：

4 结果与讨论

为了验证所提出方法的有效性，在Matlab平台上进行数值仿真。

利用3个混沌函数产生的CRPM如图2所示。从图2可以看出，每个混沌函数生成具有不同种子值的2个CRPM。Logistic映射产生的CRPM通过式（5）生成，其中第1个CRPM种子值x=0.341，第二个CRPM种子值x=0.241；帐篷映射产生的CRPM通过使用式（9）生成，其中第1个CRPM种子值x=0.610，第2个CRPM种子值x=0.620；Kaplan⁃Yorke映射产生的CRPM通过式（12）—（13）生成，其中第1个CRPM种子值x=0.200 5，y=3 005，第2个CRPM种子值x=0.200 0，y=3 000。

图2 利用3个混沌函数产生的CRPM

GT的数值算法需基于GT的光学设置进行数值模拟。在GT的光学设置中，使用了3个间距固定的广义透镜，利用谱传播方法对自由空间中Fresnel衍射进行模拟，并对广义透镜的作用进行适当的相位调制项。GT算法的性能使用标准的Lena图像进行旋转来检验，振幅数据、相位数据恢复的图像振幅如图3所示。

图3 振幅数据、相位数据恢复的图像振幅

图3（a）表示旋转45°和90°的振幅数据重构图像的振幅，图3（b）表示旋转45°和90°的相位数据重构图像的振幅。对于加密和解密过程，第1种GT的旋转角度和第2种GT的旋转角度分别为45°和90°。

利用2种方法来研究不正确的解密过程。3个混沌函数加密图像、解密图像及不正确解密图像如图4所示。第1种方法是解密过程中使用不正确的旋转角度来执行，通过在2个旋转角度中引入0.02°的误差，来计算用于解密系统的不正确的旋转角度；第2种方法是通过交换CRPM在解密过程中的位置来执行。由于混沌函数的CRPM的种子值非常接近，所以采用第2种错误解密方法研究了该技术对种子值的敏感性。

图4 3个混沌函数加密图像、解密图像及不正确解密图像

从图4可以看出，即使旋转角度引入很小误差，也不可能成功解密，因此旋转角度可作为1个密钥；如果2个CRPM的位置互换，则图像解密不成功。因此，混沌函数对于初始条件非常敏感，CRPM的种子值也可以作为1个密钥。

所提方法的性能由数值进行评估，输入图像和输出图像之间的均方差（MSE）经常被用来验证重构图像的质量，其定义为：

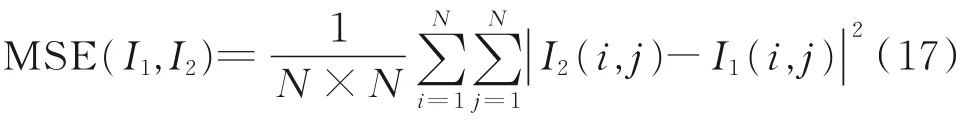
式中，I1(i,j)、I2(i,j)分别为输入图像和输出图像在像素(i,j)处的值；N×N为图像的像素总数。

MSE首先利用正确的解密参数来计算，Logistic映射加密图像与原始图像的MSE为3.26×104，解密图像与原始图像的MSE为0；帐篷映射加密图像与原始图像的MSE为3.24×104，解密图像与原始图像的MSE为0；Kaplan⁃Yorke映射加密图像与原始图像的MSE为3.25×104，解密图像与原始图像的MSE为0。

5 盲解密算法的鲁棒性

为了评估算法对盲解密的鲁棒性，计算了解密图像与输入图像的MSE。引入不同误差的解密图像与原始图像的MSE如图5所示。从图5可以看出，在2个旋转角中引入误差b(b=±0.02°)增加了MSE的值。因此，旋转角作为密钥可以保护盲解密的数据源。

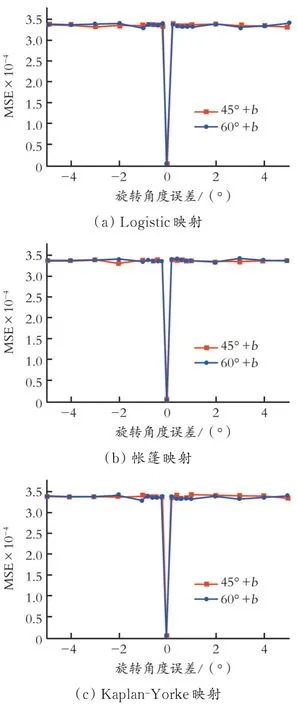
图5 引入不同误差的解密图像与原始图像的MSE

6 所提方法的光学实现

GT可由3个广义透镜和2个固定的只有空间间隔构成的光学系统执行，每1个广义透镜都是由2个相同功率的薄圆柱透镜组合成。第1个和第3个广义透镜是相同的，它们的焦距f等于设置的2个连续广义透镜之间的距离z；第2个广义透镜的焦距f2=z/2，前2个透镜通过相对于彼此旋转来给出旋转角度；第3个透镜是固定的，用于补偿旋转图像不希望得到的相位调制。这种相位调制是通过前2个透镜的旋转而引入，第1个圆柱透镜与垂直轴形成的角度为φ1，第2个圆柱透镜与垂直轴形成的角度为φ2。如果角度φ表示圆柱透镜的对称轴的位置，那么，第1个圆柱透镜的轴与垂直轴形成角度为φ1=-φ，第2个圆柱透镜的轴与垂直轴OY形成角度为φ2，由φ2=-(φ1+π/2)导出。式（1）—（2）中的旋转角度α使用式（18）来计算：

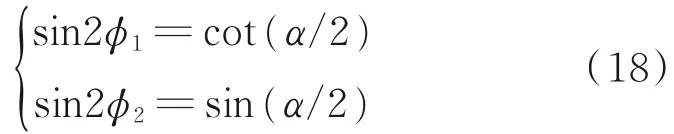
第一和第二透镜的旋转如图6所示。其中，L1和L2分别表示第一和第二透镜。

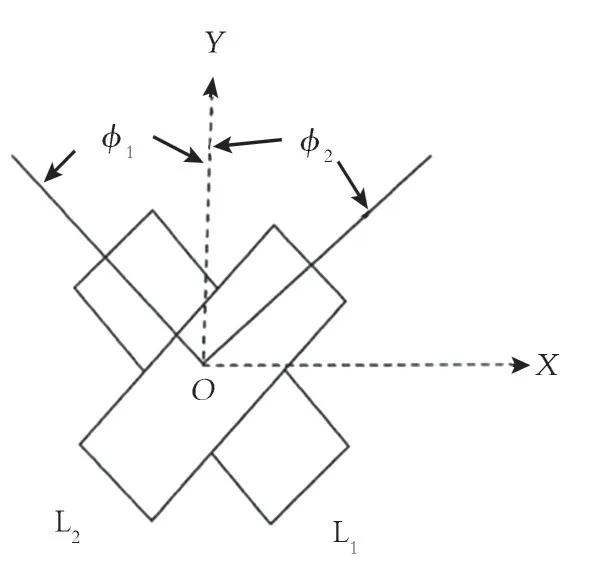
图6 第一和第二透镜的旋转

本文方法的光学实现如图7所示。

图7 本文方法的光学实现

用激光作相干光源，用分束器BS1和BS2将激光分为两部分，分束器的一个臂用作参考光束，另一个臂用作目标光束，R1和R2分别是分束器BS1和BS2的参考光束，M1、M2和M3为3个反射镜，光折变晶体（PRC）用于存储光学数据。在加密过程中，遮光器S1关闭，遮光器S2打开，被加密的图像与第1个CRPM相结合，并显示在第1个SLM1上，用透镜L1、L2和L3来执行第1次GT操作，第2个CRPM显示在第2个SLM2上，用透镜L4、L5和L6来执行第2次GT操作，该图像与参考光束R2结合，存储在PRC中，并记录在电荷耦合器件（CCD1）相机中；在解密过程中，采用相位共轭读出方案，在这个过程中，遮光器S1打开，遮光器S2关闭，光束A2从反射镜M2反射，并作为参考光束R2的共轭，从而产生与图像承载光束A4成比例的光束A3，相位共轭光束同时携带与整个加密图像相关的全部信息，当存储信号的相位共轭通过L6、L5和L4、第2个CRPM和L3、L2和L1时，对记录在CCD2中的图像进行解密，用透镜L6、L5和L4执行第2次逆GT，用透镜L3、L2和L1执行第1次逆GT，在对解密进行输入时必须精确地消除加密过程中引入的相位变化。

7 结 论

提出一种利用旋转变换和混沌加密图像的新思路，当采用不正确的解密过程时，不能成功得到解密图像。对MSE进行了评估，根据盲解密理论，评估了CRPM种子值的初始值和GT的旋转角的鲁棒性，旋转角度作为密钥可以保护数据，在未知种子值的情况下，不能成功地解密图像。CRPM的种子值和GT的旋转角度在盲解密过程可以作为鲁棒的密钥。基于CRPM的加密技术的优点在于，只有混沌函数的种子值可以用于生成解密的CRPM，因此不需要将整个RPM发送到接收方进行解密；二维混沌函数优于一维混沌函数，二维混沌函数需要2个种子值，进一步提高了加密图像的安全性。