基于IFAHP的焦化生产过程性能评估方法研究

陶文华，王玉英，桂运金，高新域

（辽宁石油化工大学信息与控制工程学院，辽宁抚顺113001）

焦化生产是一个复杂的物理和化学变化过程，包含多个子系统。生产系统运行过程性能决定炼焦产品的质量、产量以及能源消耗。针对焦化生产过程的多性能评价方法对焦化生产及钢铁生产工业有着非常重要的意义。

目前，对焦化生产过程的研究大多关注于局部子系统的控制与建模[1⁃3]。针对当前焦化生产过程控制系统的研究所出现的单元化、部分化及缺乏控制系统性能评价环节等问题，国内学者们提出一种分层递阶智能控制系统[4]。为使各个生产过程达到最优状态，使用控制系统性能评估方案，将评估信息进行实时反馈，实现系统在线优化[5⁃6]。但是，使用的模糊评价算法未考虑评估时的不确定性因素，以及权重计算时主观因素影响较大等问题。另外，一些性能评估算法仅考虑了经济性能等少数指标，难以全面描述焦化生产过程的整体性能[7⁃8]。

本文为解决焦化生产过程中存在的指标数较多、评估较为复杂的问题，使用层次分析法（AHP）对焦化生产评价过程进行简化处理[9⁃11]。层次分析法可以通过定量专业分层分析做出更可靠的决定，尤其在处理多准则问题上具有明显优势，但针对模糊问题时效果并不理想。直觉模糊集（IFS）在处理模糊性和犹豫性时都展现了很大的优势。为充分利用直觉模糊集在处理模糊性和不确定性方面的明确优势以及AHP法在处理复杂多指标性能评价问题的能力，在分层递阶控制系统下，使用直觉模糊层次分析法（IFAHP）从经济、安全、稳定三个方面入手，选取具有代表性的全局性能指标对焦化生产过程进行性能评估，基于AHP法构建评估结构，基于直觉模糊数建立偏好关系，进行一致性检测及修正。同时，因一致性阈值在某些情况下的不合理性而引入合理的阈值，利用熵与交叉熵相结合的方法得出指标权值，进而逐步推算出目标系统所采用的方案，实现焦化生产过程整体性能评估。

1 评估体系建立

根据焦化生产实际工况及系统性能，本文提取相互独立且具有代表性的12个性能指标，依据AHP算法结构建立对应的性能评估模型。基于AHP的焦化生产过程性能评估模型如图1所示。

图1 基于AHP的焦化生产过程性能评估模型

第一层目标层要综合考虑所有控制指标，故第二层准则层从经济、稳定和安全三个方面入手，分别用B1、B2、B3表示。第三层为各个准则层指标下的分解层。经济性能指标分为焦化生产过程经济性能指标C11、焦炭质量过程能力指数指标C12、加热燃烧系统历史性能指标C13和炼焦综合生产率指标C14。稳定性能指标分为焦炉加热燃烧指标C21、火道温度偏差变化率指标C22、火道温度偏差指标C23和集气管压力偏差指标C24。安全性能指标分为基础过程控制层阀门控制器性能指标C31、最大集气管压力指标C32、最高火道温度指标C33、最高火道温度超过允许值百分比指数C34。第四层是替代方案层，代表是否进行在线优化以及在线优化的急迫程度。本文将急迫优先程度分为3个类别，分别是在线优化的高、中、低需求，可用方案集A表示，A={A1、A2、A3}。

2 直觉模糊层次分析法

使用的直觉模糊算法步骤与AHP法基本相同，直觉模糊层次分析法流程如图2所示。

图2 直觉模糊层次分析法流程

2.1 直觉模糊集相关理论

定义1 令X为非空集合，称之为直觉模糊集。其中，uA(x)与vA(x)分别代表X中元素x对于X的子集A的隶属度与非隶属度，满足如下条件：

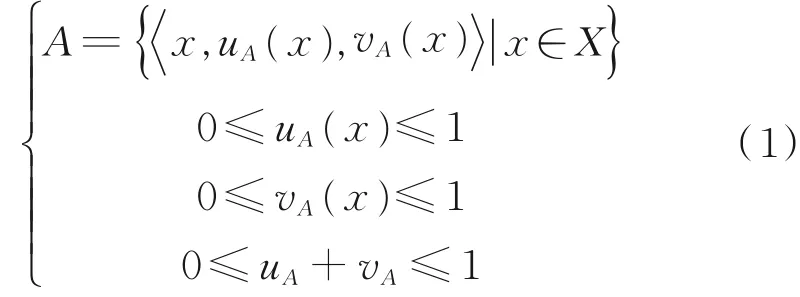
令πA=1-uA(x)-vA(x)，πA代表集合X中的元素x对于集合A的犹豫度，由隶属度、非隶属度与犹豫度构成元素，称之为直觉模糊数。

通过直觉模糊数的相似函数和精确函数，可以比较任意直觉模糊数a的大小[12]。

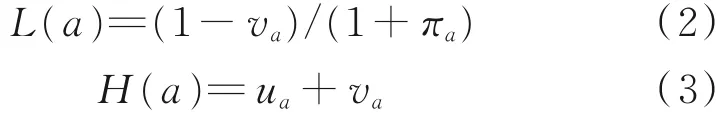
式中，L(a)为直觉模糊数的相似函数；H(a)为直觉模糊数的精确函数。

设a1和a2是两个直觉模糊数，比较方法为：

（1）若L(a1)＜L(a2)，则a1＜a2；

（2）若L(a1)=L(a2)，有以下两种情况：

2.2 直觉模糊（IF）偏好关系的建立

相较于层次分析法中成对比较法，IF偏好关系能更好地处理分配偏好时的不确定性。由文献[13-14]从数学角度给出IF偏好关系的定义可知，处于准则层第i个指标下子准则层的任意子指标p、q的IF原始偏好关系矩阵R为：

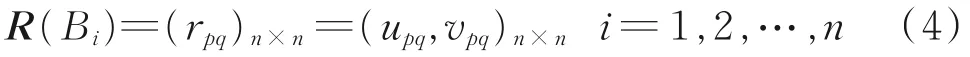
式中，rpq为直觉模糊值(IFV)；upq为隶属度，即Cip与Ciq相比较，Bi偏向于Cip的程度；vpq为非隶属度，即Cip与Ciq相比较，Bi不偏向Ciq的程度。且满足以下条件：

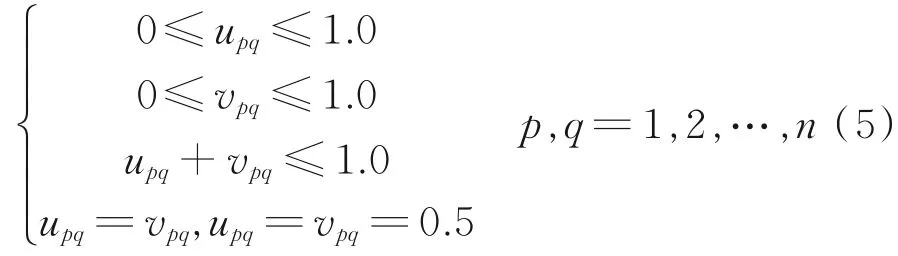
式中，n为指标Bi下的子准则层指标对应个数。

当p,q=1,2,…,n，rpq属于直觉模糊(IF)偏好关系R的直觉模糊值(IFV)，满足：

同理，使用上述方法可求出目标层所对应准则层指标(B1、B2、B3)的直觉模糊(IF)偏好关系，表达式为R(O)=(rst)m×m，rst表示准则层指标。直觉模糊标度如表1所示。决策者使用表1建立直觉模糊(IF)偏好关系。

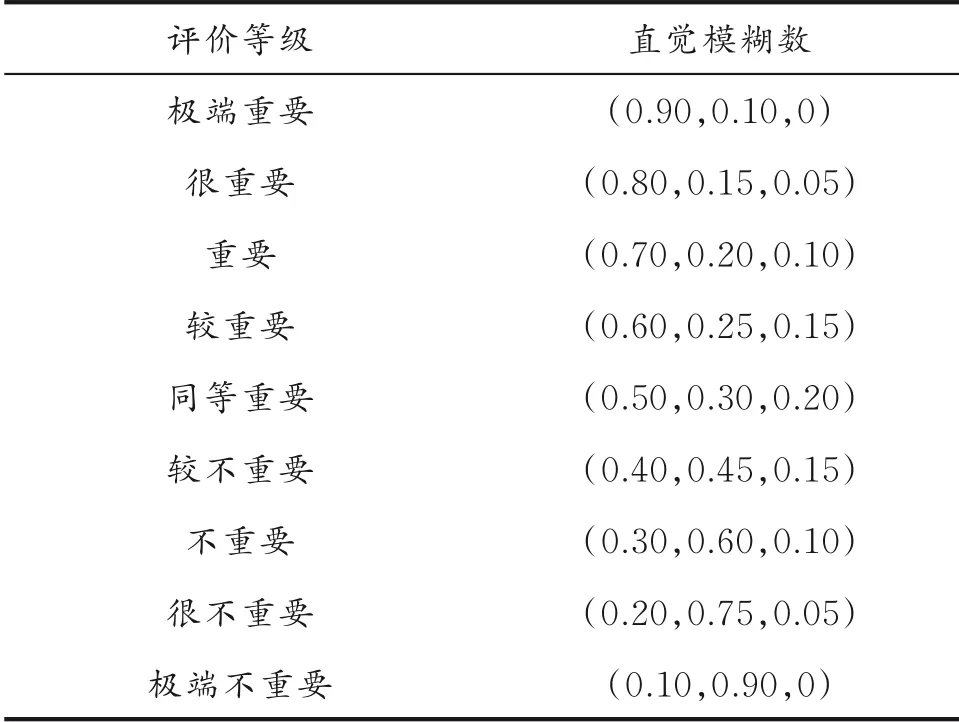
表1 直觉模糊标度

2.3 直觉模糊偏好关系的一致性检验及修正

在IFAHP法中，要想最终获取合理、可靠的结果，对直觉模糊（IF）偏好关系进行一致性检验必不可少，而一旦给出的IF偏好关系不满足可接受一致性条件，就有必要对偏好关系进行矫正，直到新的偏好关系满足可接受一致性为止。对R(Bi)和R(O)的修正步骤是相同的，统一用R(Bi)=(rpq)n×n=(upq,vpq)n×n来表示。检验及修正算法步骤为：

步骤1 当q＜p+1时，

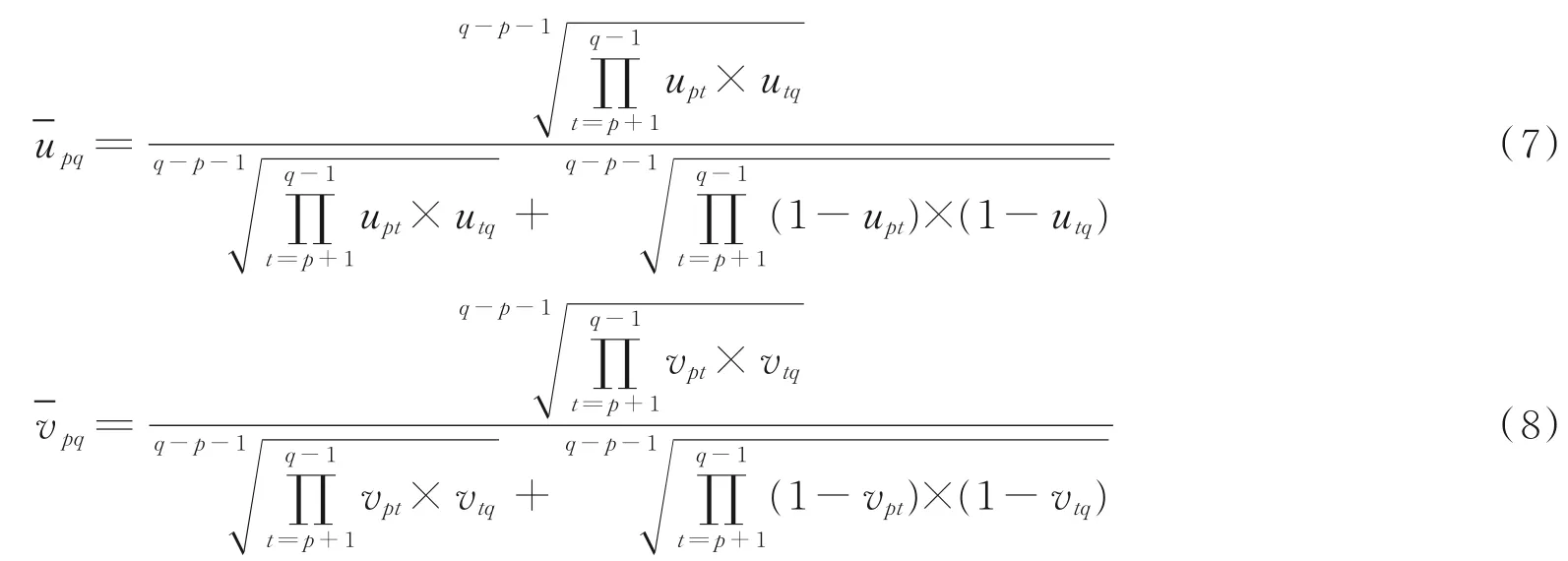
当q=p+1时，

当q≤p时，

步骤2d(R,)表示给定的直觉模糊（IF）偏好关系R到对应的完美积性一致性偏好关系的距离测度，计算公式为：

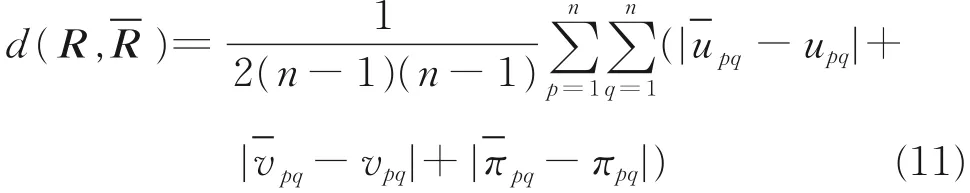
式中，πpq=1-upq(x)-vpq(x)为犹豫度，满足：

若d(R,)＜τ，则称R为可接受的一致性直觉模糊(IF)偏好关系输出结果。其中，τ是一致性阈值。相反，若d(R)≥τ，则表明R不具备一致性，需要修正原始偏好关系矩阵R。

步骤3 由于修正后的直觉模糊偏好关系不仅要具备可接受的一致性，同时要尽量保留决策者的原始信息。因此，将原始的直觉模糊(IF)偏好关系R与相组合得到一个新的IF偏好关系n×n，其中s为迭代次数，直到满足d(,)＜τ,s=1,2,…,n。当p=1时，=R，。计算方法为：

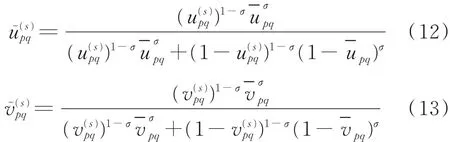
式中，σ为决策者给定的控制参数。σ∈[0,1]，σ值越小越接近R；σ值越大越接近。当σ=0时͂=R；若σ=1，则=。

2.4 基于熵与交叉熵的指标权重求解

权重计算是在满足偏好关系一致性检测与修正之后进行的，使用修正后且可接受一致性检验的偏好关系(Bi)(O)进行计算。近年来，存在着众多权重计算方法[17⁃20]，为了更大程度上避免主观影响，基于熵的方法广泛用于决策评估中。本文使用基于熵与交叉熵的方法求解权重值。

定义1E(α)为α的熵，E(β)为β的熵，IFV的熵为一个实数函数,满足：

（1）E(α)=0,有且仅有α=(0,1)或α=(1,0)；

（2）E(α)=1,有且仅有uα=vα；

（3）当uα≥uβ≥vβ≥vα或uα≤uβ≤vβ≤vα，E(α)≤E(β)；

（4）当uα=uβ=vβ=vα，E(α)=E(β)。

定义2CE(α,β)为α与β之间的交叉熵，且满足：

（1）CE(α,β)≥0；

（2）CE(α,β)=0，有且仅有α=β。

熵与交叉熵的计算公式为：

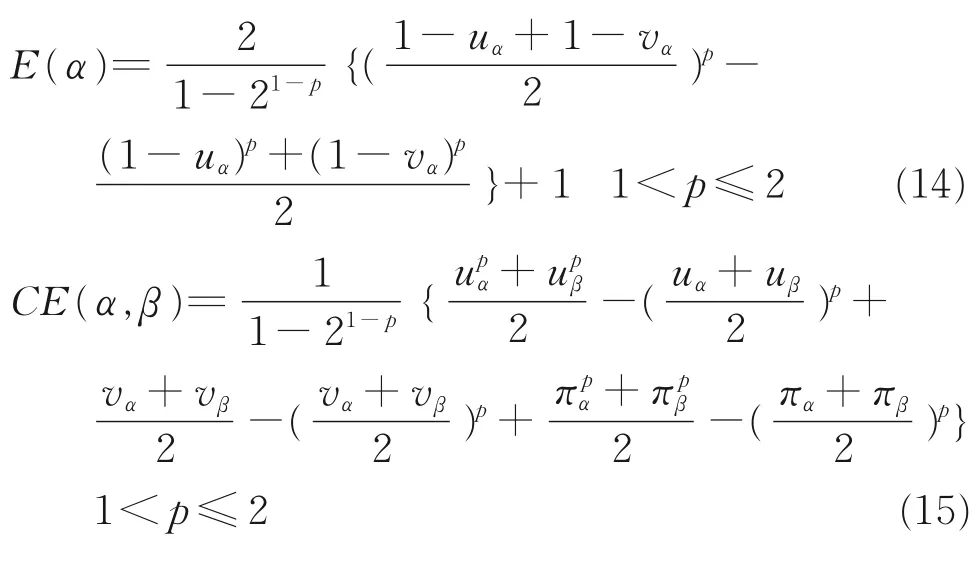
熵法用来测量直觉模糊值(IFV)信息模糊性，交叉熵法被用来测量分歧信息。设R=(rpq)n×n为直觉模糊(IF)偏好关系矩阵，r为直觉模糊值，将熵与交叉熵值代入得到指标q的权重为：

通过式(14)计算出处于Bp层次下Cpq权重wCpq以及处于目标层O下Bp的权重wBp，用WBp=(wCpq),WOB=(wBp),p,q=1,2,…,n表示，其中，WBp为Bp层次下Cpq的权重集合，WOB为处于目标层O下Bp的权重集合。

2.5 目标层及准则层性能求解

根据第p个指标的所有子指标的有关实际数据、相关算法及计算方法，计算出每个方案关于子准则层指标Cpq的直觉模糊(IF)决策矩阵，Dp(A,Cpq)=(dqk),k=1,2,…,K,q=1,2,…,n，其中K代表替代方案个数。通过Dp=(A,Cpq)与对应的WBp指标整合计算得到可选方案关于某一准则层属性Bp的决策矩阵Dp(A,B)。Dp(A,B)=Wp(B)Di(A,C)

据式（17）计算得p=1,2,3的所有D(A,B)值。同理，使用D(A,B)和W(O)，得到决策矩阵可选方案关于目标层O的权重值。

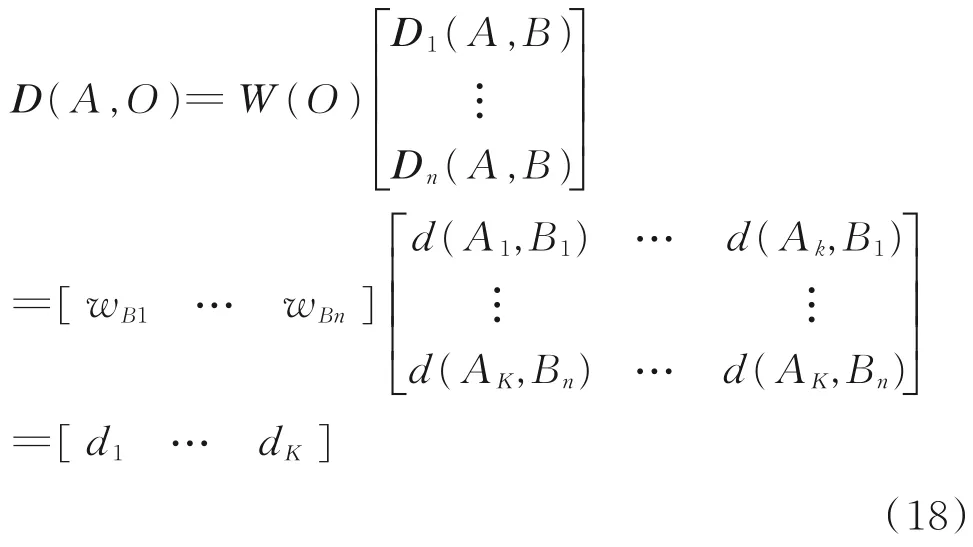
根据D(A,O)计算结果以及判断规则，决定对控制系统参数是否进行在线优化及在线优化的优先程度。利用式（1）、式（2）对D(A,O)的多个直觉模糊数进行计算，依据排序规则，得出最优方案。

3 仿真分析

为了验证IFAHP的有效性，使用JN⁃60型焦炉两种运行状态的实际数据进行指标值计算[18]。由于焦炭的质量、产量、能耗实际数据8 h采集一次，无法满足评估计算要求，因此在评估之前要进行这三类数据的预测，得到的预测数据按照指标计算公式，计算出属性指标实际值，再根据隶属度、非隶属度计算公式得到选择方案关于子准则层的决策矩阵。

3.1 直觉模糊偏好关系的建立

对焦炉实际运行状况进行评估时，基于专家经验结合表1进行成对比较，建立直觉模糊偏好关系，如表3—6所示。

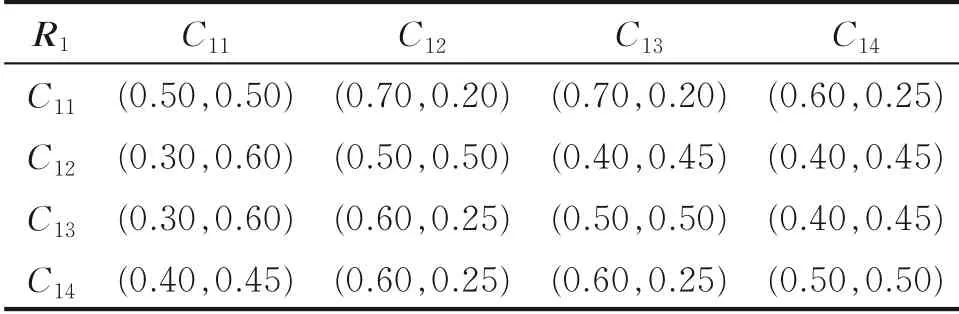
表3 指标B1的子准则层指标IF偏好关系

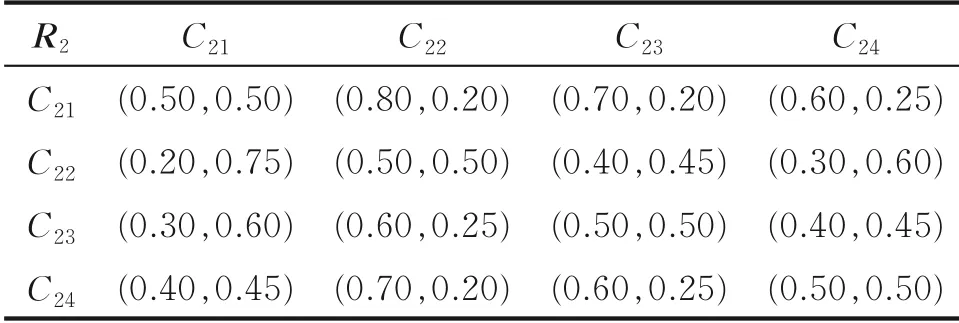
表4 指标B2的子准则层指标IF偏好关系

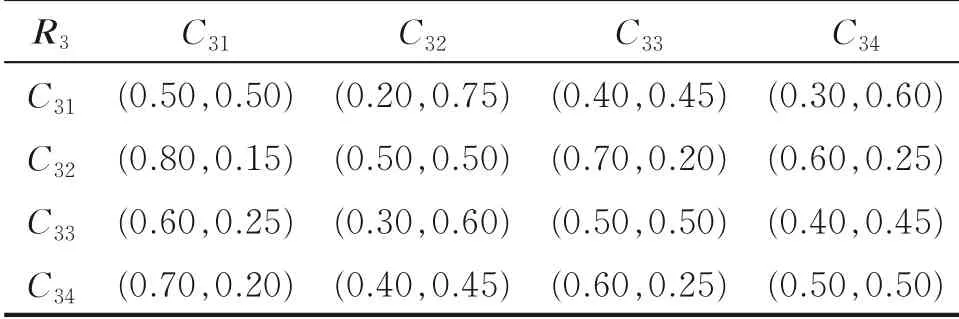
表5 指标B3的子准则层指标IF偏好关系

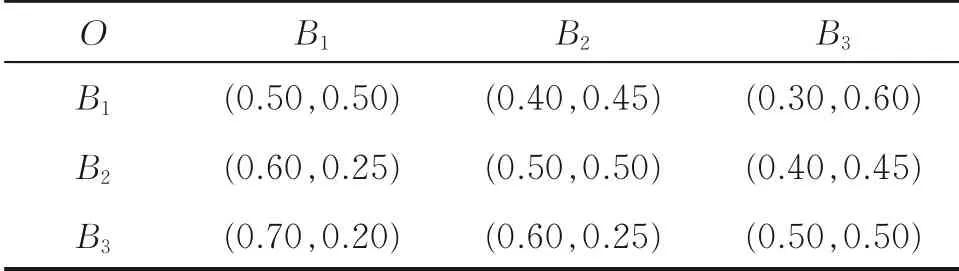
表6 准则层指标的IF偏好关系

由于计算步骤过多，无法一一描述，在这里仅采用R1进行IF偏好关系一致性检验和修正。

通过式（7）—(10)计算出对应的完美积性一致性IF偏好关系为：

根据式(11)计算得d(R1,)=0.236 8。通过表2可知，d(R1,)＞τ4h=0.084 5，进行一致性修正，取σ=0.7，经过迭代计算，直到满足d()＜

经式(11)计算得d()=0.066 2＜0.084 5，则修正后的IF偏好关系为可接受一致性偏好关系。

3.2 指标权重的计算

同理，使用同样的方法对其他的直觉模糊（IF）偏好关系进行检验和修正，然后对修正后的关系进行权重计算，通过式(14)—(16)得出W1(B)、W2(B)、W3(B)以及W(O)的值。计算时p=1,2,3。以W1(B)为例。

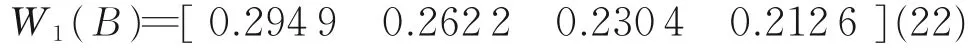
3.3 决策矩阵计算及性能状况分析

根据式（14）、式（15）求得D1(A,B)、D2(A,B)、D3(A,B)以及最终的D(A,O)。

其中，

其中，

根据以上结果可知，L(d1)＜L(d2)＜L(d3)，选择方案A3，该系统无须进行优化。取第二组数据进行评估，该数据反映受到外界干扰，火道温度出现异常，发生剧烈波动。目标层评估结果为：

根据以上结果可以得出L(d1)＞L(d2)＞L(d3)，故选择方案A1，焦化生产过程控制系统迫切需要在线优化。

4 结 论

将层次分析法与直觉模糊集方法相结合，利用AHP方法处理多个待定实施方案和许多评估方案实施效果的指标属性所构成的复杂且综合的多准则决策问题的能力，来解决焦化生产过程综合性能评估问题，利用直觉模糊熵和交叉熵方法计算指标权重值，针对直觉模糊偏好关系一致性阈值不合理问题，引用新的阈值，使修正后的偏好关系更合理。结果表明，此方法能有效评估焦化生产过程性能，并适用于大多数综合多标准决策情况，但算法计算过程较为繁琐，有待进一步优化。