微型桩-连梁组合结构的边坡加固机理与内力计算方法

马华 雷国平 苏栋，3 李华林 吴泽雄 杨伟鸿 张院生

1.铁科院（深圳）研究设计院有限公司，广东 深圳 518060；2.深圳大学土木与交通工程学院，广东 深圳 518060；3.深圳大学未来地下城市研究院，广东 深圳 518060

抗滑桩是边坡加固的常用手段，微型抗滑桩（桩径100～300 mm，长径比大于30）作为典型的柔性抗滑桩，因其施工快捷、对场地适应性强、造价低等优点，近年来被广泛应用于中小型滑坡的治理中。国内外的研究一定程度上揭示了该结构的受力特性，但是对滑坡土体位移作用下微型桩纵横弯曲变形下的受力机理、桩顶连梁的影响、微型桩的临界嵌固长度等方面的研究不足，针对该结构的内力计算方法也未能合理考虑其受力特性，这在一定程度上阻碍了该结构的应用与发展。本文对国内外的相关研究进行总结，分析该结构对边坡的加固机理，并对其影响因素进行探讨，提出下一步研究的方向。

1 微型桩组合结构常见形式

微型抗滑桩组合结构的工程应用有多种形式，根据桩的排列角度分为两种类型。

1）倾斜交叉型。该类型在国外的应用较多，采用倾斜微型桩以非平行的方式排列，并在桩顶设置顶梁。根据滑坡大小可采用A 字形（A⁃frame）结构或网状结构，如图1（a）、图1（b）所示，在同一个滑坡中也可设置多级该类结构。

2）多排平行型。国内主要采用此类结构，一般将3 排及以上微型桩以平行或近似平行的方式排列，根据设置位置可分为坡面加固型和平台加固型［1］，如图1（c）、图1（d）所示。坡面加固型的微型桩可垂直于坡面或竖向设置，桩顶采用连梁连接。平台加固型则在坡面较平缓处设置微型桩群，桩顶采用连梁或顶板进行加固，处于边缘的微型桩也常采用稍微倾斜的设置。本文主要以此类多排微型桩-连梁组合结构为研究对象进行总结和分析。

图1 常见的微型抗滑桩组合结构

2 微型桩-连梁组合结构加固机理

图2 微型抗滑桩的变形特征试验

微型抗滑桩组合结构的抗滑作用来源于四个方面：①微型桩在滑面处提供较大的抗剪力［1］。②桩与土形成抗滑体，共同抵抗滑坡推力［1］。③微型桩因受剪切变形在桩与滑面相交处产生两个塑性铰（图2），导致该处桩身倾角增大，桩由受剪变为受拉，充分发挥了加筋材料的受拉优势［1，6］。④微型桩在滑面处的弯曲变形导致桩身产生纵向位移，在桩表面产生摩擦力，该力传至土体中增加了滑面处的法向力，间接产生抗滑力［7］。

由此可知，微型桩在滑坡位移作用下同时受到横向力和纵向力的影响。根据梁结构理论［8］，同时受轴向力P和横向力Q作用的梁在弯曲变形较大时，因轴向力产生的二次弯矩不可忽略，该梁的变形属于纵横弯曲变形，如图3（a）所示，其中δ为梁的最大挠度。而对于微型桩，在滑坡横向推力作用下产生弯曲变形，同时产生轴向收缩位移，并在桩土界面摩擦力的作用下产生轴向力，如图3（b）所示，其中p为桩土横向作用力；t为轴向摩阻力；δlat为桩土最大横向相对位移；δaxial为桩土最大轴向相对位移。由于微型桩的弯曲刚度较小，轴力导致的弯矩变化和变形不可忽略，微型桩的变形也属于纵横弯曲变形，其加固机理尚待进一步研究。

图3 梁和微型抗滑桩的纵横弯曲变形示意

3 微型桩-连梁组合结构加固的影响因素分析

3.1 微型桩与滑面法向的夹角

微型桩与滑面法向的夹角θ决定了滑坡土体运动对微型桩受力的影响。国外对A 字形微型桩的现场试验［9-10］和模型试验［11］显示，处于A 字形结构中两个不同角度的桩在受力上有较大的区别。如图4 所示，对于处于右侧的微型桩（θ＜0），土体位移有一个沿桩身纵向向上的分量，在桩表面产生沿纵向向上的摩擦力而导致微型桩受拉，而对于左侧的微型桩（θ＞0）则相反产生了轴向压力，微型桩在滑面处的轴力和剪力共同起抗滑作用。图4中F为滑坡下滑力；α为滑面倾角；u为土体位移；un、uf分别为土体相对桩的横向和轴向位移分量；V为桩在滑面处的剪力。

图4 倾斜微型抗滑桩表面摩擦力分布

Loehr 等［7］根据滑面处微型桩的简化变形模式推导了其抗滑力的简化计算方法，同时也通过弹塑性p⁃y（其中y为桩土横向相对位移）和t⁃z（其中z为桩土纵向相对位移）模型分别对微型桩的弯矩和轴力进行了分析，得到了与试验相近的结果。这种直接将滑坡位移分解的分析方法比较适用于θ较大的情况（即桩所受纵向土体位移较大），而对于国内常见的微型桩与滑动面近乎垂直的情况（即桩所受纵向土体位移较小）可能会产生较大的误差。

如图5所示的竖直微型桩，根据位移分解分析，该微型桩轴向应受压力，然而由于滑面处的弯曲变形导致桩发生了纵向收缩位移，有可能出现桩的轴向位移大于土体纵向位移分量的情况，从而改变了桩所受纵向摩擦力的方向，导致桩身受拉。这种竖直微型桩受

图5 垂直微型抗滑桩表面摩擦力分布

拉的现象已被国内多个现场监测和室内试验所证实［1，12-14］，因此有必要进行微型桩纵横弯曲变形下的受力机理研究，分析不同滑坡位移角度对微型桩受力的影响。

通过加强水土保持措施设计，合理安排施工进度与工序，抓紧落实土地整治及植被恢复，减少地表裸露时间，以减少施工过程中因降水和风等水土流失影响因素产生的水土流失。

3.2 桩顶约束

微型抗滑桩一般采用连梁或承台对桩顶进行约束，模型试验及数值仿真研究［11，15-16］表明，桩顶约束能使排桩与土体共同发挥抗滑作用，有效提高土质边坡中微型桩的加固效果，其中纵向连梁（沿滑坡方向）的作用明显高于横向连梁（垂直滑坡方向）。向波等［17］通过离心试验发现，在桩顶连梁作用下边坡安全系数提高了38.3%。桩顶约束的影响也与滑体性质有关，连梁对整体性较好的滑体作用较小，而对整体性较差的松散土体影响很大［1］。

微型抗滑桩组合结构中，一般靠近滑坡后缘的一排桩受力最大，其他排桩的受力依次减小［18］，受力大小的不同导致各排桩桩顶位移的差异。如图6（a）所示，在没有连梁的作用下，各排桩的变形存在大小差异但模式相近。而在有连梁的情况下，如图6（b）所示，桩顶的水平位移差异受到约束，连梁后缘出现向上的位移而前缘出现向下的位移［1，19］，从而起到力的传导作用（包括水平力和轴向力），若桩顶和连梁为固定连接，则还会产生桩顶弯矩。如图6（c）所示，水平力的传导导致连梁轴向受压，后缘桩的桩顶出现了较大的负向剪力而前缘出现正剪力［20］，轴向力的传递主要导致前缘的桩受压，并加强了后缘桩的受拉。王洋等［13］通过对3×3 微型抗滑桩-顶板组合结构的原位试验发现，后缘桩的最大拉力出现在桩体下部，中间排桩的最大拉力出现在中上部，而前缘桩的最大压力出现在桩体上部，并且随着推力的增大，受压区不断增大，体现了桩顶约束对轴力的传导过程。

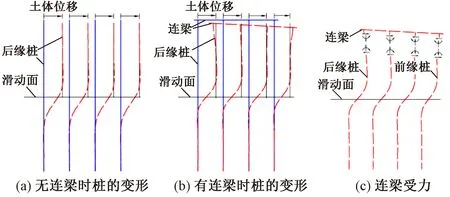
图6 连梁对微型桩作用示意

目前对于桩顶约束的影响主要以定性研究或以其对各排桩所受滑坡推力比例的定量研究［15-16］为主，连梁的存在一定程度上抑制了后缘桩的纵横弯曲变形而加强了前缘桩的变形，使组合结构的加固机理更为复杂，需要进一步的研究。

3.3 嵌固长度

微型桩嵌入滑床的长度直接影响着微型桩的抗滑能力，嵌固段除了满足微型桩水平抗力的需求外还要满足抗拔和抗压承载力的需求［21］。当嵌固长度过短时，滑面以下土体达到水平抗力极限，微型桩以整体随滑坡移动的刚性运动为主［22］［图7（a）］。当嵌固长度足够时，则需考虑微型桩抗弯强度是否满足要求［图7（b）］。Viggiani［23］研究了刚性抗滑桩最大弯矩和桩嵌固比λ（嵌固长度与受力段长度的比值）的关系，并得出了发生横向刚性运行的λ临界值。Lei 等［24］对柔性桩的λ临界值和最大弯矩进行了研究，是对微型桩嵌固长度的初步分析，但是该研究尚未考虑微型桩纵横弯曲的特性和桩顶连梁的影响。

图7 微型桩嵌固端作用示意

当微型桩嵌固长度满足横向受力的要求时，还应进行轴向抗拔或抗压验算［图7（c）］。微型桩在滑动面处的极限拉∕压力（Pult）为

式中：αf1是滑体中的桩土界面摩擦因数；L1是微型桩在滑体中的长度；d是桩径。

微型桩满足抗拔或抗压稳定需求的临界深度L2crit为

式中：αf2是嵌固段的桩土界面摩擦因数；FS是稳定性系数。

以上计算方法的缺点是没有考虑微型桩变形过程中摩擦力的真实分布以及连梁导致的微型桩轴向力的变化。

由于对微型桩-连梁组合结构的受力计算缺乏合理的定量分析模型，目前对微型桩的临界嵌固长度尚未达成统一认识。GB∕T 38509—2020《滑坡防治设计规范》建议嵌固长度不大于1∕3 总桩长，而孙书伟等［25］通过对微型桩加固土质边坡的数值模拟研究建议最优锚固长度取自由段长度的1.5～2.0倍。因此，有必要在微型桩受力机理分析和连梁作用研究的基础上探讨微型桩的临界嵌固长度，为微型桩桩长的设计提供理论支持。

3.4 微型桩间距

微型桩群的平面排列方式一般有行列式排列和品字形排列。在相同的桩间距的情况下，品字形排列的微型桩群承载力更高［14，26］，也是GB∕T 38509—2020推荐的排列方式。微型桩间距根据与滑坡方向的关系包括横向间距（垂直滑坡方向）和排间距（平行滑坡方向）。

横向间距的影响与传统大直径抗滑桩间距类似。当横向间距小于临界间距时，在滑坡推力作用下，桩间产生土拱效应而抵抗桩间土的水平运动，单桩抗滑力随间距的增加而增大［27-30］。对于大直径桩，该临界值约为4倍桩径［27］。对于微型桩，Bruce等［31］认为当桩间距为7～8倍桩径时可忽略群桩效应；何晖［18］认为桩间距为8～10 倍桩径时土拱效应最为明显；向波等［17］的离心试验显示，桩间距与边坡安全系数呈幂函数关系，并建议桩间距控制在6～12倍桩径。

杜衍庆［32］通过有限元计算，发现排间距对微型抗滑桩承载力的影响大于横向间距，排间距过小会导致微型桩整体抗弯刚度降低，排间距过大则会造成微型桩群工作性能降低，后缘桩承担较大的滑坡推力，而前缘桩不能有效发挥作用，并建议最佳排间距为5 倍桩径。朱宝龙等［5］通过离心试验也发现，排距越大后缘微型桩承受的土压力越大。何晖［18］的试验显示，排间距为5～10 倍桩径时，各排桩分担的滑坡推力比较均匀，工作性能良好。张丹丹［26］和苏媛媛［14］的试验研究表明，当排距在4～6倍桩径时微型抗滑桩组合结构水平承载力最大。

对桩间距的研究虽因试验或模拟条件的不同稍有差异，但基本认同桩间距为5～6倍桩径时微型桩抗滑性能较好，GB∕T 38509—2020 建议桩间距不小于5倍桩径，与前述研究较为相符。

3.5 其他因素

除以上因素外，微型桩的抗弯刚度、施工工艺以及滑体岩土类型等也会影响微型桩的抗滑作用。闫金凯等［33］的试验显示，由于不同配筋方式导致抗弯刚度不同，桩周配筋的微型桩在滑面处产生弯剪破坏，而桩心配筋的微型桩在滑面附近发生弯折破坏。滑坡的岩土体类型影响着滑坡的推力分布以及微型桩的受力类型。GB∕T 38509—2020 建议，对硬质岩层滑坡可假定滑坡水平推力均匀分布于各排桩；对软质岩或风化严重的岩层滑坡以及土质滑坡，应考虑作用于各排桩的不均匀性。辛建平等［34］通过数值模拟分析发现不同类型边坡中微型桩的破坏机制不同，岩土混合边坡中桩体主要在滑面处和滑面以上分别发生弯剪和弯曲破坏，岩质边坡中桩体主要发生滑带处错动引起的剪切破坏，而土质边坡中桩体主要发生滑带两侧的弯曲破坏。施工工艺中注浆的影响也比较大。在高压注浆作用下，水泥砂浆容易在滑面土层扩散形成水泥土，提高滑面抗剪强度；同时，浆液的填充和挤密作用使岩土体的孔隙减小、密度增大，形成一个扩散复合体，可有效阻止地表水渗入，提高滑坡或边坡的稳定性［17］。

4 微型桩-连梁组合结构内力计算

针对微型抗滑桩组合结构的内力计算广泛采用的方法包括平面钢架计算方法、基于桩土相互作用弹塑性p⁃y、t⁃z模型的计算方法以及数值仿真法。

4.1 平面钢架计算方法

该方法将微型抗滑桩-连梁组合结构简化为平面钢架，采用结构力学方法进行求解。冯君等［35］假设桩顶之间为弹性连接，桩与桩周岩土体相互作用采用弹性地基梁K 法或m 法，并且根据岩土体性质假设滑坡推力的分布，通过传递系数法计算桩间滑体的剩余下滑力。周德培等［1］假设滑面处为固定端，滑坡推力为均布荷载，地基土的基床系数采用K 法，桩顶轴力根据顶梁的弯矩计算，因此无法分析桩身部分轴力的变化。肖世国等［12］以滑面为界，对上半部分采用侧向弹性地基约束的平面钢架模型，假设岩土推力按三角形分布作用于平面钢架上，各桩按m 法求解内力；对下部嵌固段根据地层条件采用K 法或m 法计算，通过迭代获得整体内力计算结果，轴力则通过截面转角近似计算，与实测对比时发现后缘桩的轴力分布有一定误差。王金梅等［36］根据微型桩上各部分受力特点的不同，将微型桩分成上部摩擦受拉段、中部滑坡推力作用段和下部锚固段三段进行分析，假设滑坡推力主要作用在滑面上部一定范围并呈等三角形分布，锚固段受向下的摩擦力作用，水平方向采用横向受力的弹性地基梁进行分析。该方法的不足是不能考虑微型桩纵横弯曲作用导致的轴力变化，也没有扩展至多排桩的情况。此类方法中滑坡推力的大小和分布不能随着桩和岩土体的变形实时调整，没有考虑在大变形情况下桩土相互作用的非线性特征，对桩内力的分析没有考虑桩纵横弯曲变形的特性，不能真实反映微型桩-连梁组合结构的受力情况。

4.2 基于弹塑性p⁃y、t⁃z模型的计算方法

基于弹塑性p⁃y模型的计算方法能够较好地计算抗滑桩的横向变形。其计算原理如图8（a）所示，将桩土相互作用假设成一系列随桩身分布的横向非线性弹簧（即p⁃y模型），并通过施加土体横向位移进行计算求解。White等［37］采用LPILE 软件结合试验实测p⁃y模型得到了与试验吻合较好的计算结果。Lei 等［24］采用双曲线p⁃y模型对柔性桩的响应进行了一系列的计算分析。Boeckmann［11］、Sun 等［38］采用p⁃y法对微型桩的内力进行了计算，但是该方法只能进行单桩计算，没有扩展至多排桩结构，对于无联系梁的微型桩计算结果与实测的弯矩分布较为符合，而对于有顶梁的微型桩误差较大［11］。

采用t⁃z模型可以对微型桩的轴力分布进行分析，如图8（b）所示，将纵向桩土相互作用假设成一系列随桩身分布的纵向非线性弹簧（即t⁃z模型），弹簧参数根据桩土界面性质确定，通过施加土体纵向位移可求解桩身轴力。Loehr 等［7］采用该方法对倾斜微型桩的轴力进行了较好地预测。但是与p⁃y模型计算弯矩的效果相比，该方法对轴力的计算效果要差很多，甚至在一些情况下无法获得正确的轴力方向［11］，主要原因是该方法没有考虑微型桩纵横弯曲变形的特性，也没有合理考虑桩顶约束的影响。

图8 基于桩土相互作用弹塑性p⁃y、t⁃z模型的计算模型

总而言之，该类方法具备较好的可扩展性，能通过技术手段克服前述不足，建立考虑纵横弯曲变形和连梁作用的基于弹塑性p⁃y、t⁃z模型的微型桩组合结构内力计算方法。

4.3 数值仿真法

目前一般采用有限元或有限差分法对微型桩加固边坡进行数值模拟研究。该方法将桩和土体离散成足够小的单元体，采用梁单元或弹性实体单元来模拟桩，对岩土单元则采用弹塑性本构模型，滑坡过程采用强度折减法或通过预先设置接触面单元的形式进行模拟。该方法虽然能较好地还原微型桩加固滑坡的受力过程，但是其精度受诸多因素的影响，如土体的变形和强度参数、本构模型、桩土界面性质等，应通过原位或模型试验对数值模型进行校核。同时，数值仿真也常作为模型试验的补充，共同揭示微型桩的加固机理。目前国内外学者虽然通过数值仿真对微型桩的加固机理及影响因素进行了大量研究，但是主要以参数影响规律的定性研究为主，对微型桩桩土相互作用的研究不足，没有为微型桩-连梁组合结构的内力计算提供桩土相互作用模型。

5 结语

微型抗滑桩-连梁组合结构的研究主要是分析其加固机理及影响因素（桩倾角、桩顶约束、嵌固长度、间距等），并建立合适的内力计算方法进行优化设计。国内外研究人员通过模型和现场试验以及数值模拟等手段对该结构受力特性进行了大量的研究，提出了平面钢架计算法以及p⁃y、t⁃z模型法等方法。目前的研究表明，微型桩的抗滑承载力由滑面附近桩的剪力及轴力共同提供。由于微型桩纵横弯曲变形的特性，加上连梁作用带来的多排桩协调受力的复杂性，目前还不能准确计算微型桩的抗滑承载力，对微型桩临界嵌固长度的分析还停留在单桩极限分析阶段。因此，有必要针对以上问题进行相关的试验、模拟和理论研究，探寻考虑桩身纵横弯曲变形的微型抗滑桩-连梁组合结构内力计算方法，对该结构的优化设计提供理论和技术支撑。