旋转机械扭振检测方法的研究现状及展望
郭艳玲 邱枫 李志鹏



摘 要:旋转机械扭振是影响旋转机械工作可靠性和使用寿命的主要因素之一,近年来由于扭振引起的大型机组事故日益增多,因此如何检测扭振成为机械行业一大重点。扭振的检测过程可分为扭振信号的测量和扭振信号的提取分析这两个步骤。将扭振信号的测量方法分为接触式测量法和非接触式测量法两类,将扭振信号的提取分析方法分为基于傅里叶变化法和基于信号分解法两类,并对这几类方法中的具体每种方法进行了介绍,详细地阐述了每种方法的工作原理、研究意义、实际应用以及优缺点,最后对这几类方法的发展趋势进行了展望,希望对今后的旋转机械扭振检测方法的研究起到一定的参考和指导作用。
关键词:旋转机械;扭振;信号测量;信号提取分析;发展趋势;检测方法
DOI:10.15938/j.jhust.2021.06.007
中图分类号: TH825
文献标志码: A
文章编号: 1007-2683(2021)06-0047-08
Research Status and Prospect of Torsional Vibration
Detection Methods for Rotating Machinery
GUO Yan-ling, QIU Feng, LI Zhi-peng
(School of Electromechanic Engineering, Northeast Forestry University, Harbin 150040, China)
Abstract:Torsional vibration of rotating machinery is one of the main factors affecting the reliability and service life of rotaing machinery. In recent years, the number of large units accidents caused by torsional vibration is increasing. Therefore, how to detect torsional vibration has become a major focus in the machinery increasing.The process of torsional vibration of detection method can be divided into two steps: the measurement of torsional vibration signals and the extraction and analysis of torsional vibration signal. The measurement methods of torsional vibration signal are divided into contact measurement method and non-contact measurement method. The extraction and analysis methods of torsional vibration signal are divided into Fourier transform method and signal decomposition method. We introduce each method of these methods, espound in detail the woking principle, reaserch significance, practical application, advantages and disadvantages of each methods, and finally forecast the development trend of these methods. It is expected to provide some reference and guidance for the future research on torsional vibration detection methods of rotating machinery.
Keywords:rotating machinery; torsional vibration; signal measurement; signal extraction analysis; development trend; detection method
0 引 言
旋轉机械主要是指电动机、汽轮机、燃气轮机等机械设备。随着此类机械的应用越来越广泛,如何确保其安全稳定的运行,引起越来越多的重视。扭振对旋转机械造成很大影响,使旋转机械疲劳积累不断加强,形成裂纹、切口,并逐渐扩散,最终导致此前不容易察觉的轴系的断裂。同时,扭振会引起系统噪声增大、动力性能下降。
近年来国内外由于扭振原因引起的大型机组事故日益增多,2003-2004年,俄罗斯RAO EES Rossii电厂因扭振引起的涡轮转子出现裂纹的事故共12起,修理更换转子的费用达到3.08亿卢布[1]。2009年由于扭振造成乌兹别克斯坦塔里曼扎尔州地区发电站的800兆瓦涡轮机组被完全摧毁[1]。2010年广东茂名某热电厂200MW机组锅炉配备的风机主轴断裂,2011年该轴再次断裂,事故原因是扭转疲劳剪切断裂[2]。此类事故的发生,引起行业内的广泛重视。
扭转振动简称扭振,其主要原因是丧失了动力力矩和负载扭矩之间的平衡,合成扭矩的方向反复变化。由于旋转轴不是绝对的刚体,当旋转轴受到动力源周期性的扭转激励时,旋转轴就会按动力源激振频率强迫振动。对扭振的检测可以分为两个步骤:扭振信号的测量和扭振信号的提取分析。
1 扭振信号测量方法
扭振测量技术的起源可追溯至19世紀初,发展至今,主要可分为两大类:接触式和非接触式扭振测量法。
1.1 接触式测量方法
接触式测量法主要特点是传感元件安装于旋转轴上,通过无线收发装置或者滑环来收集所测得的扭振信号。其采用的方法主要有电阻应变片法、加速度法和光纤光栅应变片法。
1.1.1 电阻应变片法
电阻应变片法[3]起源于19世纪初,最早用于旋转轴扭矩的测量,后也可以用于扭振的测量。该方法将电阻应变片互成直角粘贴于被测轴上,如图1所示。当被测旋转轴产生弹性形变时,应变片的电阻值会产生相应的变化,阻值的变化量与被测轴形变量成一定的比例,通过这一比例可以计算出被测轴形变的大小,从而得到扭振信息。Han H S等[4]采用本方法对某船轴系扭振进行了实测,验证了该方法的有效性。
电阻应变片法可以直接测量被测轴形变量的大小,具有灵敏度高、结构简单等优点,适用于中低速工况。但电阻应变片的使用寿命有限,不适合在恶劣的条件下工作。
1.1.2 加速度计法
加速度法[5]是一种用压电加速度计作为传感器安装在旋转轴上来测量扭振的方法。该方法将两个加速度计均匀布置在被测轴的两端。通过加速度计来测量被测轴的角加速度信号,对其进行积分得到角速度信号,角速度信号即为扭振信号。
本方法灵敏度高,成本低,适用于中低速工况。相对于电阻应变片法提升了使用寿命且结构更为简单。缺点是:在工作条件受到限制时,不易于安装在主轴上。
1.1.3 光纤光栅应变片法
近年来众多专家学者针对电阻应变片不适合恶劣工况,使用寿命短,以及加速度计不易安装等缺点,致力于研究新材料检测扭振,其中光纤光栅应变片法最为主流。
本方法是一种基于光纤光栅原理的扭振测量方法,魏莉、刘芹等人设计了光纤光栅与扭振之间的应变传递模型,并根据此模型研究了光纤光栅传感器并搭建了实验台,利用差分法消除了温度对光栅应变片的影响,使其只对应变敏感。当转轴产生扭振时,通过光栅应变量与转轴扭矩变量之间的关系得到扭振信息[6]。
由于光纤光栅传感器,外形和质量小,安装简单,几乎不影响轴系的动平衡,同时不受电磁波的干扰,抗腐性强 [7],克服了电阻应变片寿命短,不宜在恶劣工况下工作和加速度计不易安装的缺点,但该测量技术成本高,其测量精度受环境影响较大。
综上3种方法相比较而言,电阻应变片法目前使用最为广泛,光纤光栅应变片法目前还处于实验阶段并不成熟,加速度计法由于加速度计安装受工况限制,未能得到广泛应用。
接触式测量法的一大优点是,可以通过传感器直接测得被测轴的扭振。但该方法却有一个难以改善的缺点,即不适合测量高转速工况,因为被测转轴的转速一旦过高,转轴离心力过大,安装在被测轴上的传感元件有脱离被测转轴的危险。所以接触式测量技术渐渐有被非接触式测量技术取代的趋势。
1.2 非接触式扭振测量方法
非接触测量方法的主要特点是传感器不与被测轴系直接相连接,适用于高速旋转轴,通常通过测量旋转轴的角速度来体现被测轴的扭振信息。
1.2.1 脉冲时序法
脉冲时序法起源于19世纪90年代,属于最早的非接触式测量技术,是综合相位差法和频数计数法的特点发展而来的。
脉冲时序法有两大类:一种是磁电式脉冲时序法[8-10],在旋转轴上安装等分齿盘,磁电式传感器充当测量工具,当转轴工作时,传感器通过感应磁通量的变化,产生一系列关于电压的周期性谐波[11-12]。另一种是光电式脉冲时序法[13-16] ,即利用光电式传感器,对旋转轴上粘贴的黑白相间的编码带进行测量,由于黑白条纹对于光的反射率不同,在传感器上产生相应高电平信号和低电平信号,也可测的一系列周期性谐波。
光电式测量法,灵敏度相对于磁电式更高,但是不易于应用于恶劣的工作条件。磁电式测量适合在恶劣条件下,但在旋转轴上安装等分齿盘较为麻烦,而且等分齿盘具有一定的质量,可能会引起旋转轴的结构特性改变。
A. L. Nazolin等[15]基于光电式脉冲时序法原理建立一个扭振监测系统,对某300MW的汽轮机组进行了扭振监测,验证了该方法的有效性,并给出了后续一些列的改进性建议,推动了此技术的发展。
张玉皓等[17]提出了一种脉冲信号输出的广义增量编码器模型,用于测量旋转机械的瞬时角速度,优化了传统脉冲时序法的实时性。并在国内2台1000MW的汽轮机发电机组上实施了检测,验证了该方法的有效性。
脉冲时序法目前在行业内应用最为广泛,代表产品有英国的TV-1、美国的TVSC型扭振仪等。与此同时这一测量技术也存在一些明显的缺点需要完善:
1)条纹码,等分齿轮存在制造误差[18],或是转速产生波动时,会造成测试结果失真,进而产生测量误差。
2)本方法不适合测量旋转轴的低速工况,近几年为了改善上述缺点众多专家学者进行了大量的研究和实验。
DIAMOND D H等[19]提出了一种计算方法, 该方法采用了贝叶斯线性回归来计算条纹带的增量距离,并经过模拟实验得到验证,结果表明,该方法可以准确地确定转轴上任意不规则形状的条纹带,有效的弥补了光电时序法由于条纹带不规则形状带来的误差。
田忠旭等[18]针对磁电式传感器采集的类似余弦波的电压信号,提出了一种不断向零电压靠近的双线逼近算法,给出了转速计算的谐次提取算法,研究了瞬时转速各阶谐波函数的变化规律,可以有效去除由等分齿轮误差所造成的信号坏点。经过在四缸汽油机的扭振测试结果表明,该方法具有较高的适应性与稳定性。LI K等[20]设计了一款基于电磁感应信号的角度传感器。利用了感应线圈对旋转磁场的反馈原理,实现了同时满足同时适用于高转速和低转速角度测量。并通过实验验证得出结论,该角度传感器可以测量1 r/min到100 r/min的速度范围,为磁电式脉冲时序法测量低转速工况迈出了重要的一步。
FU Y.C等[21]设计了一款电容传感器,其探头采用差动多层环形结构,增加了微板的正面积提高了传感器的测量精度及范围。分别进行了大量程和小量程的标定实验,分析了不同的拟合方法的非线性误差,验证了设计的合理性,为将来磁电式脉冲时序法传感器的选用方面提供了有价值的参考。
ONA Denis Ijike等[22]通过对传统电涡流传感器探头中线圈间隙的调整,提高了电涡流传感器探头的灵敏度,这一方法对今后的磁电式脉冲时序法精度提高的有着重大的意义。
1.2.2 激光测扭法
激光测扭法[23-24]是一种基于激光多普勒技术的扭振测量方法,将激光投射到被测轴的一个截面上,反射光形成多普勒频移,该频移与旋转轴转速成正比。通过光学配置如图2,使相邻两个时刻所形成的多普勒频移光信号在光学探测器上产生光学混频,光电流时间差正比于转轴在两个时刻的速度差,由于相邻的光电流时间差极小,因此可以直接获得角加速度,这一角加速度反映了轴系角速度的变化,进而获取轴系的扭振的信息。
1.2.3 CCD扭振测量法
基于CCD技术的扭振技术测量[25]:该方法首先需要在被测旋转轴上标记一条螺旋线,作为CCD摄像机的被测物。旋转轴工作时,螺旋线会在CCD摄像机上呈一系列斑点,当扭振存在时,斑点的分布是非均匀的,即斑点的运动不处于匀速状态,通过计算斑点的瞬时角加速度,通过数据处理,从而获得旋转轴的扭振信息。
本方法的优点是精度高,实时性好,稳定性强,信息量大,可一次性测量多个转轴面。但是目前为止,该方法未能应用于实际工程当中,没有相应产品问世,可靠性方面没有得到验证。
非接触式测量技术是当今行业内的主流技术,综上所述三种非接触式扭振测量技术,脉冲时序法测量稳定,工程上易实现,现有产品最多,应用范围最广;激光测扭法灵敏度高,响应速度快,但是价格昂贵。CCD测量技术精度高,实时性好,但工程应用少,可靠性未得到验证。
2 扭振测量信号提取分析方法
无论采用以上哪一种扭振测量方法,其最终测得的结果都是一个输出信号,得到相应的信号如何消除噪声,提取有用信息也是研究的一大重点[26]。
传统的傅里叶变换法应用广泛,但仅适用于线性稳定系统,对于非线性非稳定系统,传统傅里叶变换法则受到了很大的局限性[27]。对于非线性非稳定信号,目前多数使用时频分析的方法来进行分析。
常用的时频分析法主要包括两类,一类是以傅里葉变换为基础的方法,另一种是以经验模态分解(empirical mode decomposition,EMD)为基础的方法。
2.1 基于傅里叶变换法
此类方法早起最有代表性的是短时傅里叶变换和小波变换,这些方法能一定程度上解决了傅里叶变换在处理非线性非稳定信号时的局限性,但是短时傅里叶变换的窗函数大小固定,无法同时满足较高的时间分辨率和频率分辨率,小波变换也面临着小波基选取的问题,二者都不具有自适应性[28-32]。
近年来诸多专家学者针对这类问题展开了深入的研究,S变换,同步挤压变换等方法相继问世。
2.1.1 S变换,广义S变换
S变换[33]是Stockwell于1996年提出的时频分析算法, S变换采用高斯窗函数,其宽度可以随信号频率变化,相比较其他方法无需选择窗函数,同时克服了短时傅里叶变换窗函数大小固定的缺陷,所以无论是对于信号中的低频部分还是高频部分,S变换过滤后的信号较短时傅里叶变换及小波变换所得到的信号都更为准确,分辨率更高,无损性,降噪性能好。但是S变换中高斯窗口会随着频率的增大而变窄,进而导致频率的分辨率降低[34]。
为了克服S变换的这一缺点,Pinnegar等引入调节因子λ对高斯窗函数进行改进,提出了广义S变换,通过调节λ使高斯窗函数随频率的变化自适应调整以获得最佳时频分辨率,适合处理非线性,非平稳的振动信号[35-36]。
2.1.2 同步挤压小波变换
本方法是2011年Daubechies在小波变换的基础上提出来的,根据时间-尺度平面每个元素绝对值的大小,对平面中的能量进行重新分配,最后根据映射公式将时间-尺度平面转化为时间-频率平面[37-38]。
本方法的优点是信号时频聚集性及分辨性强,同时受不确定准则的限制较小,因此该方法时频联合域比其他分析方法的时频分析方法的联合域要大,受到广泛使用。与此同时,本方法的结果也在一定程度上受到小波基的影响,反映高频弱振幅的信息能力不足。
2.1.3 同步挤压S变换
针对上述S变换和同步挤压变换的不足,近年来提出了同步挤压S变换,该方法将S变换和同步挤压变换结合起来,无需选择小波基,改善了同步挤压小波变换结果受小波基影响的缺点,同时也克服了S变换时频分辨率不足的缺点。目前,该方法是基于傅里叶变换发展起来的一种最优方法,在处理分析振动信号中极为有效。
潘高元等[39]运用了该方法对美国Case Western Reserve University电气工程实验室中的相关轴承的实验数据进行了分析,证明了该方法优点的真实性。
以上基于傅里叶变换所演化过来的一类方法的共同特点是要选取预先设定好的基函数来表达原始信号,存在自适应不足,时频分辨率低的问题,虽然同步挤压S变换可以在很大程度上克服这些问题 ,但还是存在这方面的弊端。
2.2 基于EMD信号分解法
此类方法是基于经验模态分解法 [40-41](empirical mode decomposition,EMD)的一类方法,EMD法是依据数据自身的时间尺度进行信号分解,相对于基于傅里叶变换法,无需选取基函数,具有自适应性强的优点,非常适合处理非线性非平稳信号。但是存在端点效应及模态混叠现象,严重影响了分解结果的正确性。近年来,众多专家学者在此方法的基础上进行改进从而克服以上不足。
2.2.1 集合经验模态分解法,完全集合经验模态分解法
集合经验模态分解法(ensemble empirical mode decomposition,EEMD)在EMD法的基础上在信号中加入了白噪声,白噪声具有频率均匀分布的统计特性,使信号在尺度分布上连续不断,改变其在极点上的特性,增强了信号的内捷性,有效地避免了模态混叠的现象,但是添加的白噪声残留会给信号带来噪声干扰。
张超等[42]采用本方法对某钢铁公司电机的滚动轴承做了故障诊断,将故障轴承的非稳态原始振动信号进行了分析,并与EMD方法做了比较,可以更快的提取轴承损伤性故障特征。验证了该方法的有效性。
完全集合经验模态分解法[43](complete ensemble empirical mode decomposition,CEEMD)与EEMD的过程一样,不同之处在于在添加一种白噪声之后再加上一组相反符号的噪声,再按照EMD分解得到固有模态函数(intrinsic mode function,IMF),该方法不仅解决了模态混叠问题,而且对原始信号进行了精确的重构,也可以部分的抵消白噪声带来的噪声干扰,是在EMMD方法的基础上所做的改进。
2.2.2 希尔伯特-黄变换
希尔伯特-黄变换(Hilbert-Huang transformation, HHT)方法起源于1998年[44],近年来被广泛的应用于处理振动信号。该方法包含了经验模态分解法和希尔伯特变换两部分计算,其简要过程是可分为如下步骤:
1)采用经验模态分解方法将测得的扭振信号分解为一些固有模态函数(IMF),这些函数是满足一定条件的分量;
2)对每一个IMF进行Hilbert变换,得到相应的 Hilbert谱,换言之就是将每个IMF表示在联合的时频域中;
3)将所有IMF的Hilbert谱归纳在一起就会得到原信号的Hilbert谱。
HHT在处理非线性非平稳扭振信号上优势显著,本方法由EMD和希尔伯特变换两部分组成,EMD的模态混叠缺点一定程度上也会影响到HHT的精度[45]。
2.2.3 希尔伯特振动分解法
希尔伯特振动分解(Hilbert vibration decomposition,HVD)是Feldman等[46]在小波分析和HHT时频分析方法的基础上总结出的一种非平稳信号分析的时频分析方法。该方法简要步骤如下[47-48]:
1)对扭振原始信号进行Hilbert变换,从而获得其解析信号。
2)需要对原始信号的非平稳频率部分进行处理,可采用低通滤波的方法对其进行分离,从而获取扭振信号中最大幅值分量的瞬时频率,利用同步检测的方法取得此信号分量的初始相位以及最大振幅值。
3)利用Hilbert迭代运算检测出原始信号每个信号分量的时频信息。
肖璞等[49]对HVD法进行了优化,在HVD法三个步骤采用镜像延拓的方法对信号进行端点预处理,消除了前两个步骤所带来的边界效应,并通过信号仿真和轴承故障诊断实验验证了该方法的有效性。
本方法避免了HHT方法中复杂的EMD过程,提高了分解速度。与此同时对多分量非平稳信号进行了细致分析,分解精度也得到提高。
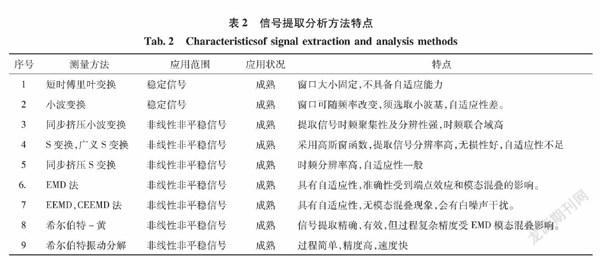
表2为各种信号提取分析方法的特点。
3 展 望
由于旋转機械领域扭振事故的频发,国内外相继提出多种扭振测量方法。随着无线遥测技术的飞速发展,接触式测量法在信号降噪方面会取得一定程度上的进步,但无法应用于高速旋转轴的检测仍是限制其发展的最大障碍。非接触式测量为当今主流技术,而在非接触扭振测量技术当中,脉冲时序计数法是当前应用最广泛,对应产品最多的一种扭振测量技术,但对于传统磁电式传感器而言,存在漏磁大、磁场强度小、测量误差大等缺点。目前基于磁聚焦技术在医疗、无线电力传输、金属表面探伤等领域开始得到应用[50-51],其特点是在很小的区域范围内形成较大的磁场强度,不存在漏磁问题,所以可以考虑利用聚焦磁场原理设计传感器,提高聚磁效率,提高传感器精度。同时用柔性电路板(FPC)粘贴在被测轴上取代传统齿轮盘,解决了齿轮盘不易安装这一缺点。对于扭振信号提取分析方法,基于傅里叶变换发展起来的方法,由于基函数的存在,始终存在自适应性不足的缺点,今后基于EMD信号分解法将逐渐成为主流技术,EMMD,CEMMD在一定程度上解决了EMD分解法的模态混叠问题。对于HHT法来讲,仍需要对EMD分解法曲线拟合方式、边界效应等问题作进一步的改善,以得到更加理想的处理效果。
参 考 文 献:
[1] KUMENKOA I. On Ways to Reduce the Risks of Operating Energy Industry Facilities[C]// Proc. 6th Seminar School- Evaluation and Control of Industrial Risks in Industrial Safety. Risk Monitoring of Complex and Unique Objects, Aug. 24-25, 2016 Omsk, Russia, 2016: 107.
[2] 唐忠顺.一次风机主轴断裂的原因分析及处理[J].风机技术,2011(4):73.
TANG Zhongshun. Reason Analysis and Disposal for Main Shaft Ruputure of Primary Fan[J]. Chinese Journal of Turbomachinery, 2011(4): 73.
[3] 周国强,甘少炜,雷伟,等. 应变测量在轴系扭转振动测试中的应用[J].船海工程,2014(2):165.
ZHOU Guoqiang, GAN Shaowei, LEI Wei, et al. Application of Shafting Torsional Vibration Measurement Basedon Strain Measuring[J]. Ship & Ocean Engineering, 2014(2):165.
[4] HAN H S, LEE K H, PARK S H. Estimate of the Fatigue Life of the Propulsion Shaft from Torsional Vibration Measurement and the Linear Damage Summation Law in Ships[J]. Ocean Engineering, 2015, 107(1): 212.
[5] 杨卓君,廖明夫.基于加速度传感器测量扭振方法的研究[J].噪声与振动控制,2008(5):163.
YANG Zhuojun, LIAO Mingfu. Measurement of Torsional Vibration Using Acceleration Sensors[J]. Noise and Vibration Control, 2008(5): 163.
[6] 魏莉,刘芹,王兢兢,等.光纤光栅应变传感在扭振测量中的应用[J].机械设计与制造,2020(4):204.
WEI Li, LIU Qin, WANG Jingjing, et al. The Application of Fiber Bragg Grating Strain Sensor in the Torsional Vibration Measurement[J]. Machinery Design & Manufacture, 2020(4): 204.
[7] 张传敏,胡国良,张涛.光栅传感器细分技术的研究[J].机械设计与制造,2017(9):159.
ZHANG Chuanmin, HU Guoliang, ZHANG Tao. Study on Subdivision Technology of Grating Sensor[J]. Machinery Design & Manufacture, 2017(9): 159.
[8] 蒋云帆,廖明夫,王四季.航空发动机转子扭振测量新方法[J].振动测试与诊断,2013, 33(3):410.
JIANG Yunfan, LIAO Mingfu, WANG Siji. New Measuring Method for Torsional Vibration of Aeroengine Rotor[J]. Journal of Vibration, Measurement & Diagnosis, 2013, 33(3): 410.
[9] 郭文新,李志深,李富才,等.基于高频采样法的轴系扭振测试新方法[J].振动测试与诊断,2017,37(6):1082.
GUO Wenxin, LI Zhishen, LI Fucai, et al. A New Method for Torsional Vibration Testing Based on the High Frequency Sampling[J]. Machinery Design & Manufacture, 2017,37(6): 1082.
[10]李建科,何國华,兰涌森,等.风力发电机组传动系统轴系扭振测量与抑制[J].船舶工程,2019,41(1):252.
LI Jianke, HE Guohua, LAN Yongsen, et al. Measurement and Suppression of Shafting Torsional Vibration of Wind Turbine Drive System[J]. Ship Engineering, 2019,41(1): 252.
[11]WU Z Y, BIAN L X, WANG S X, et al.An Angle Sensor Based on Magnetoelectric Effect[J]. Sensors & Actuators A: Physical, 2017,262:108.
[12]夏永洪,王善铭,黄劭刚,等.齿谐波绕组感应电动势波形快速计算[J].电机与控制学报,2011,15(9):1.
XIA Yonghong, WANG Shanming, HUANG Shaogang, et al. Fast Calculation of the Induced EMF Waveform of the Tooth Harmonic Windings[J]. Electric Machines and Control, 2011, 15(9): 1.
[13]杜冬.扭振信号的测试与半实物仿真[D].上海:上海交通大学,2015.
[14]王思文.基于光电式脉冲时序法的扭振测量技术研究[D].大连:大连理工大学, 2019.
[15]NAZOLIN A L, POLYAKOY C V I, GNEZDILOV S G. Diagnostics of Shaft Trains of Large Turbine Sets for Integrity Using Torsional Vibration Measurements[J]. Thermal Engineering, 2020, 67(1): 25.
[16]LISKA J, JAKL J, KUNKEL S. Measurement and Evaluation of Shaft Torsional Vibrations Using Shaft Instantaneous Angular Velocity [J].Journal of Engineering for Gas Turbines and Power, 2019,141(4):041029.1.
[17]张玉皓,顾煜炯,马晓腾,等.广义增量编码器瞬时角速度计算的扭振在线测量[J].仪器仪表学报,2020,41(10):187.
ZHANG Yuhao,GU Yujiong,MA Xiaoteng,et al. On Line Torsional Vibration Measurement Based on Generalized Incrementalencoder Instantaneous Angular Speed Calculation[J]. Chinese Journal of Scientific Instrument,2020,41(10):187.
[18]田中旭,李广州,王恒宇,等.轴系扭转振动测量的双线逼近法[J].汽车技术,2020(7):40.
TIAN Zhongxu, LI Guangzhou, WANG Hengyu, et al. Two-line Approximation for Measurement of Torsional Vibration of Shafting[J]. Automobile Technology, 2020(7): 40.
[19]DIAMOND D H, HEYNS P S, OBERHOLSTER A J. Online Shaft Encoder Geometry Compensation for Arbitrary Shaft Speed Profiles Using Bayesian Regression[J]. Mechanical Systems and Signal Processing,2016,81: 402.
[20]LI K, LI Y, HAN Y, et al. An EM Induction Hi-Speed Rotation Angular Rate Sensor[J]. Sensors, 2017,17(3): 610.
[21]FUY C, FAN W, JIN H X, et al. A New Capacitance Angle Sensor of Concentric Ring Multi-layer Differential[J].Measurement,2020,158:107625.
[22]ONADenis Ijike, TIAN G Y, SUTTHAWEEKUL Ruslee, et,al. Design and Optimisation of Mutual Inductance Based Pulsed Eddy Current Probe[J]. Measurement, 2019, 144: 402.
[23]黃震,刘彬,董全林.基于激光多普勒技术扭振测量的研究[J].光学学报,2006,26(3):389.
HUANG Zhen, LIU Bin, DONG Quanlin. Research on the Torsional Vibration Measurement Based on Laser Doppler Technique[J]. Acta Optica Sinica, 2006, 26(3): 389.
[24]LING X, YANG S, GAN C. Torsional Vibration Measurements on Rotating Shaft System Using Laser Doppler Vibrometer[J]. Optics and Lasers in Engineering, 2012, 50(11): 1596.
[25]高欣.基于CCD技术的汽轮发电机组扭振测量方法研究[D].哈尔滨:哈尔滨工业大学,2006.
[26]冯晓辉.船舶轴系扭振信号分析及应变测量系统开发[D].武汉:武汉理工大学,2018.
[27]GAO W C, LIU W, ZOU J X. Damage Detection Methods Based on Changes of Vibration Parameters: A Summary Review[J]. Journal of Vibration and Shock, 2004, 23(4): 1.
[28]QIAN S, CHEN D. Joint Time-Frequency Analysis[J]. IEEE Journals and Magazings, 1999, 16(2): 52.
[29]胡殿刚,马喜平,赵凤展,等.一种基于短时傅里叶变换的电压闪变信号的检测[J].电网与清洁能源,2020,36(3):28.
HU Diangang, MA Xiping, ZHAO Fengzhan, et al.A New Method of Voltage Flicker Detection Based on Short Time FourierTransform[J]. Power System and Clean Energy, 2020,36(3): 28.
[30]RUZZENE M, FASANA A, GARIBALDI L, et al. Natural Frequencies and Dampings Identification Using Wavelet Transform Application to Real Data[J]. Mechanical Systemsand Signal Processing, 1997, 11(2): 207.
[31]WANG Z N, KANG Y, DENG L I, et al. Investigating the Hydrodynamics of Airlift Pumps by Wavelet Packet Transformand the Recurrence Plot[J]. Experimental Thermal & Fluid Science, 2018, 92: 56.
[32]范志峰,张融,李芳环. 基于小波变换的行星轮系点蚀故障信号分析[J].煤矿机械,2020,41(9):193.
FAN Zhifeng, Zhang Rong, Li Fanghuan. Analysis of Pitting Fault Signal of Planetary Gear Train Based on Wavelet Transform[J]. Coal Mine Machinery, 2020, 41(9):193.
[33]STOCKWELL R G, MANSINHA L, LOWE R P. Localization of the Complex Spectrum[J]. IEEE Transactions on Signal Processing, 1996, 44(4): 998.
[34]凌启辉,闫晓强,张义方.基于S变换的热连轧机耦合振动特征提取[J].振动,测试与诊断,2016,36(1):115.
LING Qihui, YAN Xiaoqiang, ZHANG Yifang. Coupling Vibration Feature Extraction of Hot Continuous Rolling Mill Based on Adaptive Frequency Domain Filtering and S-Transform[J]. Journal of Vibration, Measurement & Diagnosis, 1996, 44(4): 998.
[35]PINNERGAR C R, MANSINHA L. The S-transform with Windows of Arbitrary and Varying Shape [J]. Geophysics, 2003, 68(1): 318.
[36]陳换过,易永余,陈文华,等.基于广义S变换的齿轮箱轴承故障诊断方法[J].中国机械工程,2017,28(1):51.
CHEN Huanguo, YI Yongyu, CHEN Wenhua. et al. Fault Diagnosis Method of Gearbox Bearings Based on Generalized S-transform[J]. China Mechanical Engineering, 2017, 28(1): 51.
[37]沈薇,陶新民,高珊,等.基于同步挤压小波变换的振动信号自适应降噪方法[J].振动与冲击,2018,37(14):239.
SHEN Wei, TAO Xinmin, GAO Shan, et al. Self-adaptive De-noising Algorithm for Vibration Signals Based on Synchrosqueezed Wavelet Transforms[J]. Journal of Vibrations and Shock, 2018, 37(14): 239.
[38]DAUBECHIES I, LU J F, WU H.T. Synchrosqueezed Wavelet Transforms: An Empirical Mode Decomposition Like Tool[J]. Applied and Computational Harmonic Analysis, 2011, 30(2): 243.
[39]潘高元,吕舜酩,安增辉,等.滚动轴承冲击特征提取的同步挤压S变换方法[J].振动工程学报,2020,33(2):433.
PAN Gaoyuan, LV Shunming, AN Zenghui,et al. Impact Feature Extraction from Rolling Bearing Fault Signal by Synchrosqueezed S-transform[J] Journal of Vibration, 2020,33(2):433.
[40]LI Y, XU M, LIANG X, et al. Application of Bandwidthemd and Adaptive Multiscale Morphology Analysis for Incipient Fault Diagnosis of Rolling Bearings[J]. IEEE Transactions on Industrial Electronics, 2017, 64(8): 6506.
[41]陈宗祥,陈明星,焦民胜,等.基于改进EMD和双谱分析的电机轴承故障诊断和实现[J].电机与控制学报,2018,22(5):78.
CHEN Zongxiang, CHEN Mingxing, JIAO Minsheng, et.al. Fault Diagnosis of Motor Bearing Using Modified Empirical Mode Decomposition and Bi-spectrum[J]. Electric Machines and Control, 2018, 22(5):78.
[42]张超,陈建军,郭迅,等.基于EMMD分解的滚动轴承故障诊断[J].机械强度,2012,34(5):650.
ZHANG Chao, CHEN Jianjun, Guo Xun, et al. Composite Fault Diagnosis For Bearing of Electric Machine Based on EMMD[J].Journal of Mechanical Strength, 2012, 34(5): 650.
[43]孙晓娟,王利.基于CEEMD小波包算法的降噪方法研究[J].计算机与现代化,2020(9):73.
SUN Xiaojuan, WANG Li. A Denoising Method Based on CEEMD Wavelet Packet[J]. Computer and Modernization, 2020(9):73.
[44]HUANG N E.Theempirical Mode Decomposition and the Hilbert Spectrum for Nolinear and Nonstationary Time Series Analysis[J]. Proc.R.Soc Lond A, 1998, 454(1971): 903.
[45]郝东升.希尔伯特黄变换在风机故障诊断的应用[J].内燃机与配件,2016,35(7):44.
HAO Dongsheng.Application of Hilbert-Huang Transform in Fault Diagnosis of Air Blower[J]. Internal Combustion Engine & Parts,2016,35 (7): 44.
[46]FELDMAN M. Time-Varying Vibration Decomposition Andanalysis Based on the Hilbert Transform[J]. Journal of Soundand Vibration, 2006, 295(315): 518.
[47]唐贵基,庞彬.基于改进的希尔伯特振动分解的机械故障诊断方法研究[J].振动与冲击,2015,34(3) : 167.
TANG GuiJi, PANG Bin. A Mechanical Fault Diagnosis Method Based on Improved Hilbert Vibration Decomposition[J]. Journal of Vibration and Shock, 2015, 34(3): 167.
[48]ZHU X X, YUAN Y M, ZHOU P, et al. An Improved Hilbert Vibration Decomposition Method for Analysis of Rotor Fault Signals[J]. Technical Paper, 2017, 39: 4921.
[49]肖璞,殷立.改进的HVD在滚动轴承故障诊断中的应用[J].控制工程,2020,27(2):264.
XIAO Pu, YIN Li.Application of Improved HVD in Fault Diagnosis of Rolling Bearings[J]. Control Engineering of China, 2020, 27(2): 264.
[50]REN W, MOHAMMED S I, WERELEY S, et al. Magnetic Focus Lateral Flow Sensor for Detection of Cervical Cancer Biomarkers[J]. Anal, Chem, 2019, 91: 2876.
[51]JUNG Haejoon, LEE Byunghun. Optimization of Magnetic Field Focusing and Null Steering for Selective Wireless Power Transfer [J]. IEEE. Transactions on Power Electronics, 2020, 35(5): 4622.
(編辑:王 萍)
收稿日期: 2020-10-13
基金项目: 国家自然科学基金(52075090).
作者简介:
郭艳玲(1962—),女,教授,博士研究生导师;
李志鹏(1963—),男,教授,博士研究生导师.
通信作者:
邱 枫(1990—),男,硕士研究生,E-mail:15004528946@163.com.
3673501908247

