无保持架球轴承变速曲面设计及仿真分析
赵彦玲 张晓楠 秦生



摘 要:针对无保持架球轴承滚动体之间接触碰撞的问题,提出在外圈滚道设计变速曲面,使滚动体有规律地进行减速、加速运动,进而使滚动体自动分散。分析了滚动体在径向载荷作用下时变位移规律,基于Hertz理论对轴承各零件间的作用力进行分析,建立了滚动体与局部变速曲面之间的接触力方程,揭示了变速曲面环向跨度角与接触力之间的关系,并进行变速曲面结构参数的设计。基于改进无保持架球轴承几何参数进行动力学虚拟仿真验证,分析任意3组相邻滚动体分散间距和任一滚动体加速度变化曲线,验证了变速曲面结构参数设计的正确性。本文的研究成果对无保持架球轴承的设计具有一定的指导意义。
关键词:无保持架球轴承;变速曲面;时变位移;接触力;仿真分析
DOI:10.15938/j.jhust.2021.06.005
中图分类号: TH113.2
文献标志码: A
文章编号: 1007-2683(2021)06-0033-07
Design and Simulation Analysis of Variable
Speed Surface of Cage-free Bearing
ZHAO Yan-ling, ZHANG Xiao-nan, QIN Sheng
(School of Mechanical and Power Engineering, Harbin University of Science and Technology, Harbin 150080,China)
Abstract:During the operation of cage-free bearing, the contact collision between the adjacent rollers may reduce the bearing life. Therefore, this paper propose the design of variable speed surface in outer ring raceway so that rollers can decelerate and accelerate regularly, and then rollers can be dispersed automatically. This paper specifically analyzes the time-varying displacement law of rolling body under radial load and the force between each bearing component. Based on Hertz theory, the equation of contact force between the roller and variable speed surface is established, and the variation of contact force during the rolling motion is revealed to determine the circumferential span angle of variable speed surface, which can be used to design the structural parameters of variable speed surface. Based on simulated analysis of the improved cage-free bearing geometry parameters, this work verifies the correctness of structural parameters design of variable speed surface by analyzing and comparing the changing curves that the dispersion spacing of any three groups adjacent roller and acceleration of any roller. The research results of this paper have certain guiding significance for the design of cage-free bearing.
Keywords:cage-free bearing; variable speed surface; time-varying displacement; contact force; simulated analysis
0 引 言
滾动轴承被广泛应用于各类设备中[1-10],随着我国机械行业的快速发展,对滚动轴承性能的要求越来越高,为了进一步优化轴承设计,国内外学者针对滚动体与内外圈的接触力与轴承内部结构的关系开展广泛研究。
哈尔滨理工大学赵彦玲等[11]利用ADAMS软件对钢球全表面螺旋线展开机构进行运动学仿真,并基于Hertz理论建立钢球与核心零件展开轮的接触碰撞模型[12-13],从接触力角度揭示了球面展开原理;张艳芹等[14-15]应用动网格技术和FLUENT软件研究了静压轴承在油膜厚度变化过程中的承载特性;邓彪等[16]通过有限元计算得出了滚珠数量的增加导致滚珠与滚道之间最大接触应力减小的结论;印度学者Anoopnath等[17]利用解析法和MESYS工具分析计算深沟球轴承与内圈间的赫兹接触应力;Choe等[18]研究了保持架质量分布不均对保持架稳定性的影响;王黎钦等[19]定量地分析了变工况下动量轮用球轴承保持架的运行稳定性,得到了失重状态下保持架与套圈的碰撞加剧,保持架涡动增加的结论。王稳等[20]通过实体接触条件下的轴承动态仿真分析,获得了滚珠与内圈、外圈及保持架之间的接触力动态分布规律;李庆忠等[21]以最大接触应力为目标函数,进行了球轴承内、外圈沟道曲率半径的优化设计;河南科技大学李明磊、邓四二教授等[22]设计了一种新型的轮毂轴承外圈结构,得到了弧形槽优于矩形槽的结论。为了避免保持架所带来的摩擦阻力和保持架的不稳定性,近年来国内外出现了无保持架球轴承,周彬等[23]在STR中桥主锥上应用了无保持架圆柱滚子轴承,德国FAG公司已经将无保持架陶瓷球轴承应用在微型涡轮喷气发动机上。为解决轴承滚动体互不接触和摩擦的问题,日本空宇轴承公司设计了新型轴承,并进行了摩擦系数和寿命对比试验。洛阳轴承研究所丁建强等[24]设计了一种新型满装圆柱滚子轴承,该种轴承无保持架也没有外圈结构,并且使滚子数量增多,提高了承载能力以及轴承刚度,并且避免了加工时的尺寸偏差。
综上所述,国内外虽已有无保持架轴承的生产应用,但关于无保持架球轴承的相关理论研究较少。因此本文进行无保持架球轴承中滚动体与变速曲面间接触力的分析,以优化滚动体与变速曲面之间的接触力及相邻滚动体互不接触为目标,设计两种变速曲面结构参数方案,利用ADAMS软件仿真,验证变速曲面结构参数设计的正确性。
1 滚动体与变速曲面接触力分析
以6206型深沟球轴承为例,由于变速曲面对滚动体作用原理相同,矩形变速曲面具有代表性并且易于加工,故在径向轴承外圈最下端设计一个矩形变速曲面。为了研究变速曲面环向跨度角与接触力之间的关系,建立只在径向力作用下滚动体与变速曲面间的时变位移、时变接触力方程,以此进行变速曲面结构参数的设计。
1.1 局部变速曲面引起的时变位移
如图1所示为滚动体经过变速曲面时的接触点数量变化。
如图2所示,Y轴对应的位置角为φ0,ωi为内圈旋转角速度,ωc为滚动体公轉角速度,滚动体与变速曲面始边接触时记球心为点O1,对应的位置角为φ1,滚动体以点A为圆心绕其旋转,进入变速曲面,当滚动体与变速曲面始边和两侧边同时接触时记球心为点O2,位置角为φ2,滚动体继续向前运动,滚动体与变速曲面两侧边和变速曲面终边同时接触时记球心为点O3,位置角为φ3,滚动体与变速曲面终边接触之后,会以变速曲面终边上点B为圆心旋转,并退出变速曲面,滚动体位于变速曲面终边时记球心为点O4,位置角为φ4,此时滚动体与内外滚道同时接触。若轴承滚动体数量为Z,第i个滚动体在任意时刻t的位置角φdi的表达式为
φdi=2πZ(i-1)+ωct,i=1,2,…,Z(1)
假设滚动体直径为Dw,外滚道沟曲率半径为ro,内圈滚道沟底直径为di,轴承节圆直径为dm,变速曲面轴向跨度角为θ2。滚动体从O1运动到O2时公转滚过的圆周角记为进入角Φ1,径向接触间隙位移从零逐渐增大到δmax,滚动体以恒定接触半径从O2运动到O3,此时滚动体位于变速曲面内,径向接触间隙位移保持δmax不变,其表达式为
δmax=r20-r0sinθ22212-Dw22-r0sinθ22212+Dw2-r0(2)
滚动体从O3运动到O4时公转滚过的圆周角记为退出角Φ2,径向接触间隙位移从δmax减小到零,根据变速曲面的对称性可得:
φ1=φ2=2arcsinrodisinθ22(3)
滚动体公转一周过程中,径向位移变化量δ的表达式为:
δ=δmax2-dmδmaxDwtanφ12-(mod(φdi,2π)-φ1),
φ1≤mod(φdi,2π)≤φ2
δmax,φ2<mod(φdi,2π)<φ3
δmax2-2dmδmaxDwtan(φ4-mod(φdi,2π))-φ22,
φ3≤mod(φdi,2π)≤φ4
0,其他角位置(4)
利用式(4)即可得出滚动体在变速曲面处与外滚道之间的接触位移量。
1.2 滚动体与局部变速曲面间接触力分析
当且仅当滚动体与滚道之间存在接触变形时才会产生Hertz接触力,故接触力Fi的表达式:
Fi=K·(δi)n(5)
式中:K为轴承总刚度系数,δi为第i个滚动体的弹性接触位移量。
由于局部变速曲面引起了时变位移,故轴承系统的载荷—变形关系式(5)就变为
F(t)=Kδn(t)(6)
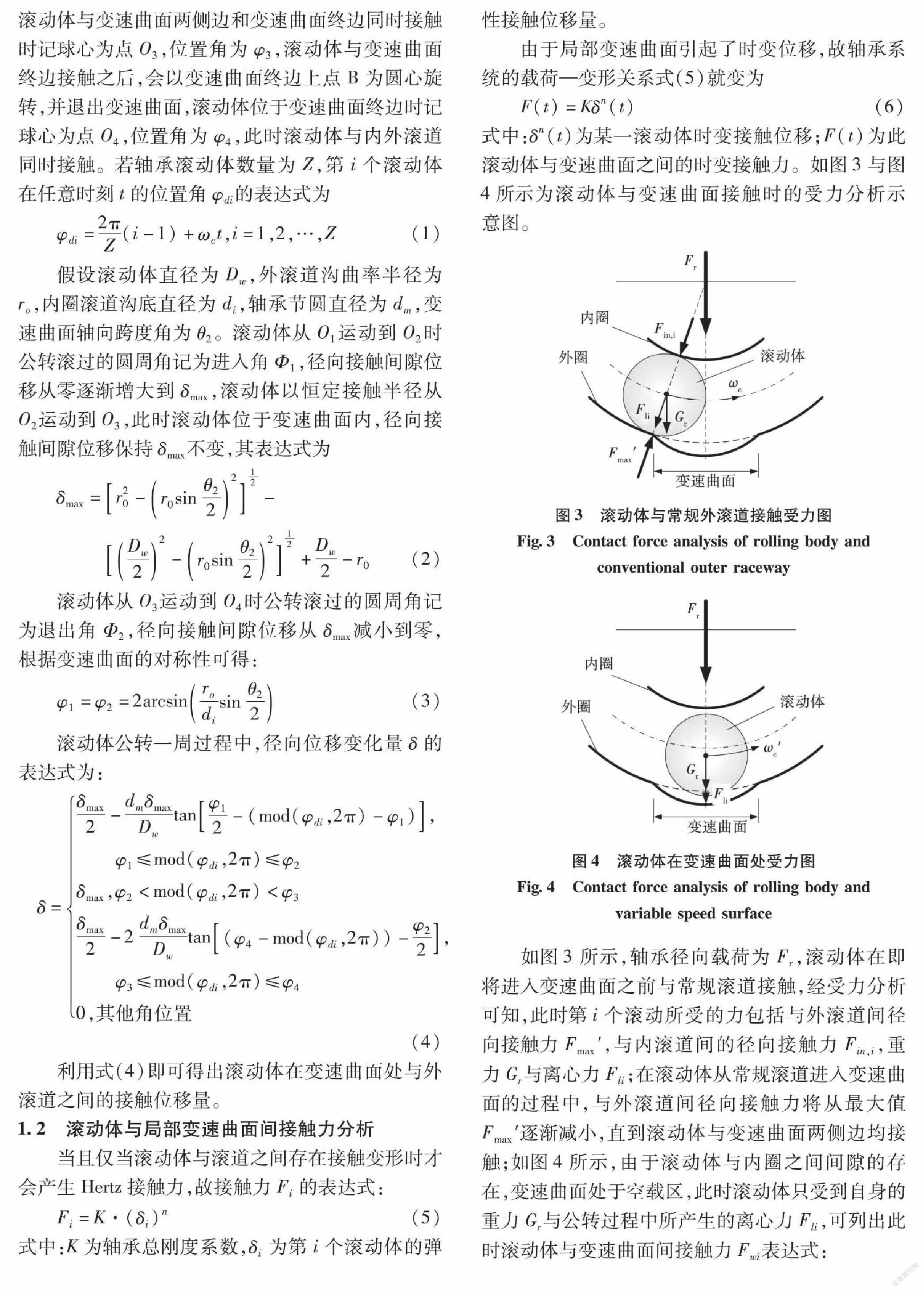
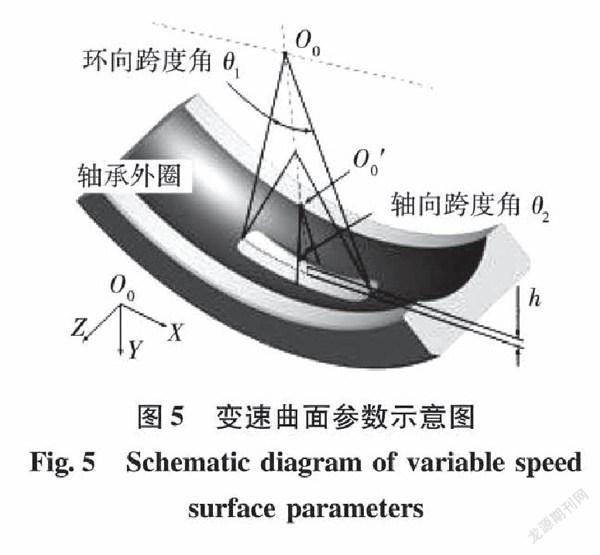
式中:δn(t)为某一滚动体时变接触位移;F(t)为此滚动体与变速曲面之间的时变接触力。如图3与图4所示为滚动体与变速曲面接触时的受力分析示意图。
如图3所示,轴承径向载荷为Fr,滚动体在即将进入变速曲面之前与常规滚道接触,经受力分析可知,此时第i个滚动所受的力包括与外滚道间径向接触力Fmax′,与内滚道间的径向接触力Fin,i,重力Gr与离心力Fli;在滚动体从常规滚道进入变速曲面的过程中,与外滚道间径向接触力将从最大值Fmax′逐渐减小,直到滚动体与变速曲面两侧边均接触;如图4所示,由于滚动体与内圈之间间隙的存在,变速曲面处于空载区,此时滚动体只受到自身的重力Gr与公转过程中所产生的离心力Fli,可列出此时滚动体与变速曲面间接触力Fwi表达式:
Fwi=dmmballω2c2+mballgcosφdi,φ2≤mod(φdi,2π)≤φ3(7)
对于正常轴承,当径向载荷为Fr时,滚动体与滚道最大接触力Fmax的表达式:
Fmax=5ZFr(8)
位于变速曲面处的滚动体卸载,故无保持架球轴承中滚动体接触力最大值为
F′max=Fmaxcosθ12=5FrZcosθ12(9)
由式(9)可知,变速曲面的结构参数直接影响滚动体接触力的大小,接触力的大小又反映在滚动体加速度的大小上。处于常规滚道中的滚动体速度大于变速曲面之内的滚动体速度,从而使滚动体分散,故为了保证相邻滚动体保持合适的分散距离,并且滚动体能退出变速曲面,在一定的范围内,加速度越大越好。因此,在变速曲面的设计过程中,必须考虑它的结构参数对接触力的影响。
2 变速曲面设计
在无保持架球轴承变速曲面的设计过程中,根据滚动体与变速曲面接触几何关系确定滚动体数量与变速曲面环向跨度角的范围,根据变速曲面环向跨度角与滚动体最大接触力的关系,进行变速曲面结构参数的设计。
设两滚动体接触时切点到轴承形心的距离为dn/2,由于Z个滚动体之间有Z个间隙,因此假设轴承内部滚动体全部接触,滚动体圆周跨度角为β,首尾两滚动体间隔在以dn为直径的圆上圆周总间隙S为
S=(360°-Z·β)·π·dn360°(10)
假设滚动体与变速曲面接触时的有效半径为Δr,则滚动体在常规滚道上的滚动圆周周长为C1,在变速曲面处的滚动圆周周长为C2,通过几何分析法可知,相互接触的两个滚动体经过变速曲面产生的分散间隙Δδ的表达式为
Δδ=θ1πdn360°-θ1πdn360°C1·C2=θ1πdn360°1-2ΔrDw(11)
对于滚动体数量,轴承圆周总间隙要保证每个滚动体全部分散的最小间隙,且除去改间隙时,轴承不能再装进滚动体,故结合式(10)和(11)可得轴承满足自分散条件时,滚动体数量Z需满足的关系式为
S-βπdn360°Δδ<Z<SΔδ(12)
为保证变速曲面中仅有一个滚动体,变速曲面环向跨度角θ1需满足:
θ1≤2arcsinDwdm(13)
由于轴承滚动体只与变速曲面两侧边接触,故变速曲面深度h需要满足:
h>δmax(14)
根据上述理论分析,现对轴承外圈变速曲面进行设计,表1为改造的无保持架球轴承几何参数及尺寸数值。
由于滚动体在非承载区会反复出现超前与滞后的现象,超前与滞后基本在区间[-0.2mm,0.2mm]内发生[25],为了防止退出变速曲面之后的滚动体因为超前或滞后而发生碰撞,本文将滚动体最小分散间距设为0.4mm,即Δδ取0.4mm,理论最小分散球心距为9.925mm。结合式(10)、(12)知滚动体数量Z需满足:Z∈(13.49,14.45),取Z为14。结合式(13)知θ1的最大值约为24°。
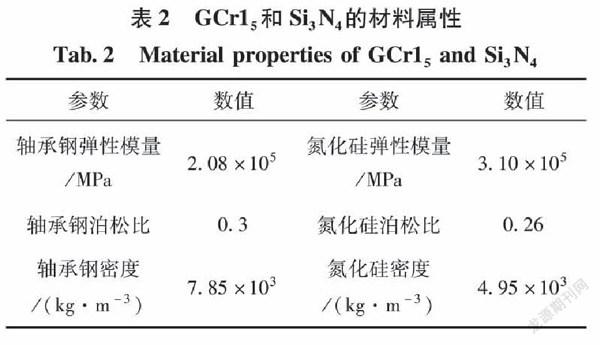
由式(9)可知,在径向载荷与滚动体数量确定的情况下,无保持架球轴承中滚动体接触力最大值随着变速曲面环向跨度角θ1的减小而增大,如图5所示,结合改进的无保持架球轴承相关参数,本文设计2种变速曲面结构参数方案,方案一中变速曲面环向跨度角θ1为24°,轴向跨度角θ2为41.4°;方案二中变速曲面的环向跨度角θ1为16°,轴向跨度角θ2为49.9°。由式(2)、(14)知轴向跨度角越大其深度也就越深,故以方案二为标准,设计深度h约等于0.015mm。
3 基于ADAMS轴承仿真分析
3.1 仿真模型的建立及参数确定
1)几何模型的创建。根据第2章设计的2个变速曲面参数方案及表1所示改进的6206型轴承相关参数,利用proe三维软件创建带有变速曲面的无保持架球轴承。
2)材料属性的定义。仿真模型导入之后,需要对模型与仿真环境进行调整设置,并修改材料属性,本文设计的无保持架球轴承内、外圈为轴承钢(GCr15)材料,滚动体为氮化硅(Si3N4)陶瓷球,如表2所示,按照表中所给出的数值对模型相应部位设置材料属性;由于旋转轴和径向力加载机构只是起到加载作用,因此对其材料无要求,本文为方便研究将旋转轴和径向力加载机构材料设置为Adams材料库自带的金属材料。
3)设置约束和驱动。在设置仿真环境与材料属性之后,需要对模型进行约束设置,在本文的研究中,内圈与旋转轴一起旋转,外圈与轴承座固定,且外圈承受纯径向载荷,因此首先将轴承外圈与大地之间固定连接,在轴承内部,滚动体与内、外圈以及滚动体与滚动体之间添加接触,旋转轴与轴承内圈之间采用固定连接,旋转轴与径向加载机构之间添加接触约束;其次在旋转轴与径向加载机构之间添加旋转副,并添加旋转驱动,最后在径向力加载机构上添加径向载荷,设置内圈转速为1200r/min,仿真时间4s,仿真步数为7200。
3.2 轴承滚动体分散仿真分析
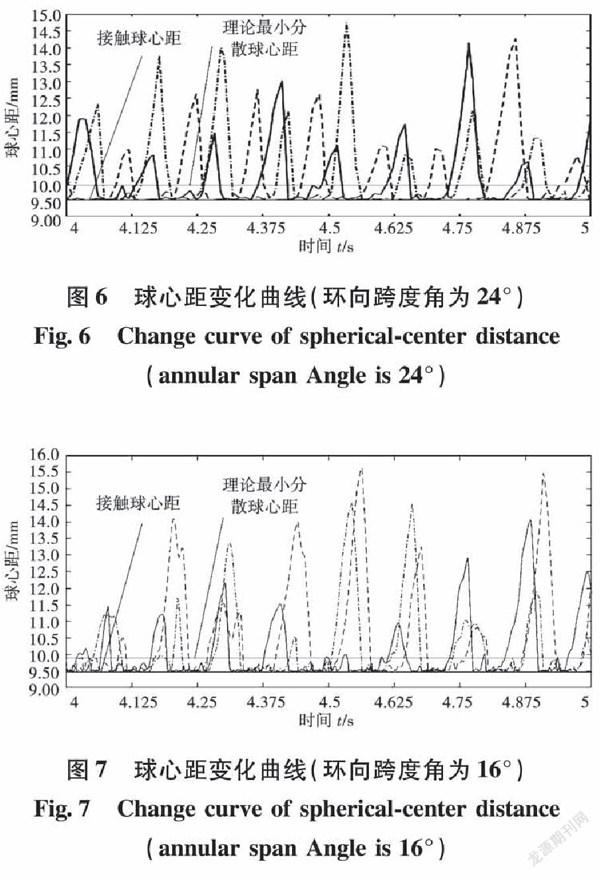
任意取3组相邻两滚动体,测量其球心距,结果如图6与图7所示。
由图6与图7可知,相邻滚动体间球心距大于接触球心距9.525mm,说明2种变速曲面的设计方案都可以实现轴承滚动体互相不接触。将图6与图7进行对比,滚动体分散距离基本都超过了理论最小分散球心距9.925mm,说明2种设计方案都可以防止滚动体因为超前或滞后而发生碰撞,并且随着变速曲面环向跨度角的增大,分散效果越好。
3.3 轴承滚动体加速度仿真分析
为了研究轴承运行过程中,滚动体速度变化的规律,并验证滚动体接触力与变速曲面环向跨度角的关系,分别对2个方案轴承中任一滚动体的加速度进行仿真分析。
由图8和图9可以看出滚动体运动加速度具有明显的周期性,且在变速曲面处存在突变,可知两种方案均能使相邻滚动体在经过变速曲面之后产生速度差,从而互不接触,验证了变速曲面结构参数设计的正确性。对比图8与图9,随着变速曲面环向跨度角从16°到24°的变化,滚动体在变速曲面处加速度与其在常规滚道的加速度皆呈增大趋势,由于接触力的变化直接反映在加速度的變化上,说明滚动体与变速曲面间接触力随着变速曲面环向跨度角的增大而减小,仿真结果与理论分析一致。
4 结 论
通过几何法揭示了滚动体在径向载荷作用下的时变位移规律,基于Hertz理论建立了滚动体和局部变速曲面之间接触力方程,揭示了变速曲面环向跨度角与滚动体接触力的关系,根据滚动体与变速曲面接触几何关系确定了滚动体数量与变速曲面环向跨度角的范围,并设计了2种变速曲面结构参数方案。基于ADAMS进行轴承运动学仿真,得到了任意3组相邻两滚动体之间的球心距以及任一滚动体振动加速度变化曲线,验证了轴承运行过程中相邻滚动体满足互相不接触的条件,得出了滚动体与变速曲面之间接触力随着变速曲面环向跨度角的增大而减小的结论,验证了变速曲面结构参数设计的正确性。
参 考 文 献:
[1] WANG Changsen.Analysis Methods of Rolling Bearing[M].Beijing:China Machine Press,1987.
[2] HARRIS T A, KOTZALAS M N. RollingBearing Analysis: Advanced Concepts of Bearing Technology[M]. 5th ed. New-York: Taylor & Francis, 2007.
[3] HENMI Nobuhiko. Recent Cases of Diagnosis Method of Rolling Bearing Failure[J]. The Proceedings of the Machine Design and Tribology Division meeting in JSME,2016,16.
[4] AKHAND Rai, UPADHYAY S H. A Review on Signal Processing Techniques Utilized in the Fault Diagnosis of Rolling Element Bearings[J]. Tribology International,2016,96:289.
[5] 李軍宁. 高速滚动轴承打滑失效问题研究进展[J]. 煤矿机械,2017,38(3):144.
LI Junning. Review of Skidding Damage Problems in High Speed Rolling Bearings[J]. Coal Mine Machinery,2017,38(3):144.
[6] 李颂华, 韩光田, 孙健, 等. 金刚石砂轮磨削轴承用ZrO2陶瓷表面质量研究 [J]. 金刚石与磨料磨具工程, 2019, 39(6):75.
LI Songhua, HAN Guangtian, SUN Jian, et al. Study on Surface Quality of Zirconia Ceramics Used for Bearing Ground by Diamond Grinding Wheel [J]. Diamond & Abrasives Engineering, 2019, 39(6): 75.
[7] 杨威, 朱建辉, 师超钰, 等. 砂轮表面磨粒出露高度对轴承钢磨削振动的影响 [J]. 金刚石与磨料磨具工程, 2019, 39(5): 73.
YANG Wei, ZHU Jianhui, SHI Chaoyu, et al. Effect of Abrasive Particle Exposure Height on Grinding Vibration of Bearing Steel [J]. Diamond & Abrasives Engineering, 2019, 39(5): 73.
[8] 葛培琪,毕文波,郑传栋.精研加工参数对轴承滚道表面残余应力影响[J].金刚石与磨料磨具工程,2016,36(5):42.
GE Peiqi,BI Wenbo,ZHENG Chuandong. Influence of Superfinishing Parameters on Residual Stress of Bearing Raceway[J]. Diamond & Abrasives Engineering, 2016,36(5):42.
[9] 李颂华,王维东,吴玉厚,等.金刚石油石超精加工氧化锆陶瓷轴承沟道的仿真与实验研究[J].金刚石与磨料磨具工程,2018,38(4):64.
LI Songhua, WANG Weidong, WU Yuhou, et al. Simulation and Experimental Study on Diamond Stick Superfinishing Bearing Raceway Made of Zirconia Ceramic[J]. Diamond & Abrasives Engineering, 2018,38(4):64.
[10]邓福铭,邓雯丽,杨雪峰,等.PCBN刀具高速切削淬硬轴承钢的磨损机理研究[J].金刚石与磨料磨具工程,2016,36(5):50.
DENG Fuming,DENG Wenli,YANG Xuefeng, et al. Wear Mechanism of the PCBN Cutting Tools in High Speed Cutting of Hardened Bearing Steel[J]. Diamond & Abrasives Engineering, 2016,36(5):50.
[11]赵彦玲, 车春雨, 铉佳平, 等. 钢球全表面螺旋线展开机构运动特性分析[J]. 哈尔滨理工大学学报,2013,18(1):37.
ZHAO Yanling, CHE Chunyu, XUAN Jiaping, et al. Kinematic Characteristics Analysis of Ball Full-surface Helical Deployment Mechanism[J]. Journal of Harbin University of Science and Technology,2013,18(1):37.
[12]赵彦玲, 李积才, 赵志强, 等. 钢球展开机构的接触碰撞特性[J].哈尔滨理工大学学报,2015,20(6):37.
ZHAO Yanling, LI Jicai, ZHAO Zhiqiang, et al. Contact and Collision Characteristics of Steel Ball Spreading Mechanism[J]. Journal of Harbin University of Science and Technology,2015,20(6):37.
[13]ZHAO Yanling, XIA Chengtao, WANG Hongbo, et al. Analysis and Numerical Simulation of Rolling Contact Between Sphere and Cone[J]. Chinese Journal of Mechanical Engineering,2015(3).
[14]张艳芹, 孔祥滨, 郭丽丽, 等. 基于动网格方法的不同油膜厚度下静压轴承承载特性分析[J].哈尔滨理工大学学报,2017,22(6):20.
ZHANG Yanqin, KONG Xiangbin, GUO Lili, et al. Bearing Characteristics Analysis of Hydrostatic Bearing with Different Oil Film Thickness Based on Dynamic Mesh Method[J]. Journal of Harbin University of Science and Technology, 2017,22(6):20.
[15]ZHANG Yanqin, SUN Jichang, KONG Pengrui, et al. The Dynamic Simulation and Experiment of Bearing Capacity of Multi Oil Cushion Static Bearing with Double Rectangular Cavities[J]. Industrial Lubrication and Tribology, 2019(9).
[16]DENG Biao, GUO Yuan, ZHANG An, et al. Finite Element Analysis of Thrust Angle Contact Ball Slewing Bearing[J]. Materials Science and Engineering, 2017:274.
[17]ANOOPNATH P R, BABUB V S, VISHWANATH A K. Hertz Contact Stress of Deep Groove Ball Bearing[J]. Matertals Today,2018,5(2):3283.
[18]CHOE B, KWAK W, JEON D, et al. Experimental Study on Dynamic Behavior of Ball Bearing Cage in Cryogenic Environments, Part Ⅱ:Effects of Cage Mass Imbalance. Mechanical Syst Signal Process,2019, 116: 25.
[19]張志强, 王黎钦, 张传伟, 等. 变工况过程中球轴承保持架的稳定性[J].工程科学学报,2019,41(11):1458.
ZHANG Zhiqiang, WANG Liqin, ZHANG Chuanwei, et al. Stability of Ball Bearing Cage in Variable Working Conditions[J]. Journal of Engineering Science,2019, 41(11):1458.
[20]王稳,李维. 考虑接触特性的滚动轴承系统建模与仿真分析[J].现代制造工程,2020(3):72.
WANG Wen, LI Wei. Modeling and Simulation Analysis of Rolling Bearing System Considering Contact Characteristics[J]. Modern Manufacturing Engineering, 2020(3):72.
[21]李庆忠,朱强,李东炬.基于接触应力的氮化硅混合陶瓷球轴承曲率半径优化设计[J].机械传动,2017,41(8):100.
LI Qingzhong, Zhu Qiang, Li Dongju. Optimal Design of Radius of Curvature of Silicon Nitride Mixed Ceramic Ball Bearing Based on Contact Stress[J]. Mechanical Transmission,2017,41(8):100.
[22]李明磊,邓凯文,邓四二,等. 一种新型轮毂轴承外圈结构的淬火有限元分[J].轴承,2017(1):24.
LI Minglei, DENG Kaiwen, DENG Sier, et al. Quench Finite Element Analysis of A New Type of Hub Bearing Outer Ring structure[J]. Bearing,2017(1):24.
[23]周彬, 郭婵, 王纯, 等. 无保持架圆柱滚子轴承在STR中桥主锥上的应用[J]. 汽车实用技术,2016(12):44.
ZHOU Bin, GUO Chan, WANG Chun, et al. Application of Cylindrical Roller Bearing without Cage on Main Cone of STR Middle Axle[J]. Automobile Practical Technology,2016(12):44.
[24]丁建强, 贾松阳, 王朋伟, 等. 新型无外圈满装圆柱滚子轴承的设计[J]. 轴承, 2018(10):1.
DING Jianqiang, JIA Songyang, WANG Pengwei, et al. Design of A New Type of Cylindrical Roller Bearing Without Full Outer Ring[J]. Bearing, 2018 (10) : 1.
[25]NAKASE A, MIZUNO T, LOU L. Study on Measurement of Dynamic Performance of Ball Bearing for Auto-tensioner[J]. Jtekt Engineering Journal, 2017(1014E):39.
(编辑:温泽宇)
收稿日期: 2020-07-11
基金项目: 国家自然科学基金(51875142).
作者简介:
张晓楠(1997—),女,硕士研究生;
秦 生(1989—),男,硕士.
通信作者:
赵彦玲(1963—),女,教授,博士研究生导师,E-mail:zhaoyanling@sina.com.
3659501908296

