砂土条件下加固隧道掌子面稳定性研究

贺祚，杨栋，陈顿，刘志强，张晋龙，郑加勇，孙立武，程杰

砂土条件下加固隧道掌子面稳定性研究

贺祚，杨栋，陈顿，刘志强，张晋龙，郑加勇，孙立武，程杰

(中铁十八局集团 第五工程有限公司，天津 300451)

针对玉磨铁路的太达村隧道工程，结合普氏压力拱理论并参照三维旋转破坏机制，提出考虑土供效应条件下改进的三维旋转破坏模型对砂土条件下隧道掌子面稳定性进行研究。所提出的破坏模型可分为2部分：1) 位于交叉层的旋转破坏部分；2) 位于覆盖层的拱形破坏部分。基于本文所提出的改进破坏模型，采用岩土-锚杆模型对加固隧道掌子面稳定性进行研究。结果表明：1) 通过与现有研究结果对比可知，本文所提出模型是可靠的，且更适合砂土隧道掌子面稳定性分析；2) 通过结合具体的工程，可知本文所提出方法能够有效指导实际隧道工程砂土段隧道掌子面加固设计和施工。

普氏压力拱理论；土供效应；隧道掌子面稳定性；岩土−锚杆模型；安全系数

隧道在开挖过程中主要面临2个难题：地面沉降问题；隧道掌子面稳定性问题。针对新奥法施工方法开挖的隧道掌子面无作用力作用，主要是靠作用在隧道掌子面上的超前支护措施维持隧道掌子面的稳定性。对于新奥法施工隧道，主要是通过计算安全系数来评估掌子面稳定性。所谓的超前支护措施是基于隧道周边围岩条件、施工方法、进度要求、机械支撑等优选的一种或几种集成的辅助构造方法以加强地层进而确保掌子面稳定性[1]。目前主要的预加固措施有：超前锚杆、超前自行式锚杆、超前灌浆小管道、超前灌浆大型管棚、卧式喷射灌浆桩和超前围岩预注浆等[2−3]。近年来，国内外许多学者针对锚杆支护进行了大量的研究[4−6]。Yoo等[4]通过三维有限元方法研究了纵向锚杆加固隧道掌子面的稳定性，并给出了加固参数如锚杆密度、长度及刚度对隧道掌子面稳定性的影响。Peila[5]研究了锚杆加固隧道掌子面的稳定性，研究结果表明掌子面前方塑性区范围会随着锚杆数量的增加而减少，但是锚杆数量需要满足一定值以保证掌子面稳定。周捷等[6]采用数值模拟方法研究了锚杆参数对隧道掌子面稳定性的影响，并将成果应用于浏阳河隧道河底段的施工，研究结果表明采用锚杆加固能显著改善掌子面的稳定性。本文依托在建的玉磨铁路的太达村隧道工程，提出考虑土供效应条件下改进的三维旋转破坏模型。基于所提出模型，采用岩土−锚杆模型分析锚杆支护下砂土隧道掌子面的稳定性。最后将本文所提出方法应用于太达村隧道砂土段隧道掌子面稳定性评估。

1 工程概况

新建玉磨铁路的太达村隧道位于宁洱与普洱之间，地处哀牢山西侧与永平−思茅槽地的东南部地质构造复杂。隧道全长5 815 m，隧道最大埋深约180 m。太达村隧道为双线铁路隧道，设置一个辅助坑道，隧道平面布置如图1所示。

图1 隧道平面示意图

太达村隧道存在下第三系弱胶结砂岩，主要分布在DK240+900～DK241+784之间，且该区段地下水丰富，附近构造发育。开挖揭示成粉砂状，饱水时自稳性极差，饱水遇临空面时呈流沙状。受到不良地质的影响，太达村隧道斜井工区的掌子面施工到DK241+787时，掌子面发生坍塌，造成了掌子面开挖停工，严重影响了施工安全和施工进度。因此选择合适的加固参数来保障隧道施工的正常推进，是本工程的一个重点问题。

图2 DK241+787坍塌后掌子面

2 模型建立

由图3所示，本文所提出的改进破坏机制由2部分组成，位于交叉层的旋转破坏部分和位于覆盖层的“帽子”拱形破坏部分，以下章节对所提出改进破坏机制进行介绍。

图3 锚杆支护掌子面破坏模型

2.1 交叉层破坏部分

位于隧道掌子面交叉层的破坏机制是基于Mollon等[8]提出的离散化技术和“点生点”获得的，如图4所示。

图4 隧道掌子面及三维旋转破坏机制纵断面示意图

由图4可知，对于本文所提出的破坏模型交叉层部分的闭合需同时满足以下2个条件：1) 下一个平面的角度β大于β；2) 下一个平面ψ上的点P,j+1超出隧道拱顶即点P的纵坐标大于点的纵坐标。

图5 生成过程示意图

图6为采用“点生点”和离散技术生成的交叉层旋转破坏部分示意图。

图6 交叉层三维旋转破坏机制部分

2.2 覆盖层破坏部分

根据2.1节可知由“点生点”生成的三维旋转破坏机制可以得到一个隧道顶面轮廓(见图5)。根据三维旋转机制生成的破坏土体边界随着内摩擦角的增大，这个轮廓会逐渐偏离圆的形状，若直接将其简化成等面积圆这会导致误差增大。基于此，本章节提出隧道覆盖层拱形破坏机制(见图7)。根据图8可知，隧道顶面轮廓是关于轴对称的(图7中纵坐标即是轴)，且图中各网格点的坐标由2.1节可知。本章主要介绍所提出覆盖层拱形破坏机制部分的高度的确定。

图7 覆土层拱形破坏部分示意图

图8 掌子面交叉层三维旋转破坏部分顶面

所提出的改进破坏机制的拱形破坏部分的高度是由普氏压力拱理论确定得到的。普氏压力拱理论是拱形机制的一个重要理论依据，其主要内容是根据坍塌土体的底面直径确定土体的坍塌高度，其关系式为：

式中：为土体的坍塌高度；为坍塌区域的底面宽度；为土体内摩擦角。

由图8可知，对称轴为隧道顶面轮廓的最大宽度，因此通过对称轴起始和终端两点便可确定拱形机制底面宽度的取值，如图7所示。2.1节中已经得到顶面轮廓各点坐标，设顶面轮廓点个数为，将个点的坐标编为数组([]，[]，[])，则可以通过下式确定：

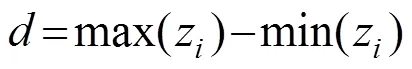
结合式(3)，所提出覆盖层拱形破坏机制部分的高度可表示为：

3 岩土−锚杆模型

本章采用的岩土−锚杆模型主要基于以下假定：

1) 将加固构件假定为一维结构单元，仅考虑其轴向力；

2) 考虑岩土−锚杆相互作用；

3) 在岩土−锚杆相互作用区，假定土是静止的，并且土与锚杆之间存在完全的黏附。

4) 在速度不连续面上，加固构件的轴向速度与周围岩土速度相同。

为了计算锚杆做功，假定一个岩土−锚杆的相互作用区来模拟土体和锚杆之间的作用(见图9)。如图9所示，左侧区域表示塌陷的刚性土体，右侧区域则是静止的刚性土体。这两个区域被一个速度不连续面即土体坍塌的滑动面隔开，滑动面上的土体速度为v。S和v分别表示锚杆的轴向位移和速度，相互作用区域的厚度为。

图9 岩土-锚杆相互作用区域示意图

根据假定，锚杆的轴向速度与土体速度满足以下关系：

式中：v表示锚杆的轴向速度；v表示土体滑动速度；β表示土体滑动速度与水平方向的夹角。

根据图10所示，考虑单个加固锚杆时，从力学平衡角度出发，其轴向应力与剪应力应满足以下关系：

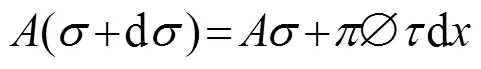
式中：σ表示锚杆轴向应力；τ表示锚杆剪切应力；A表示锚杆横截面积；f表示锚杆直径。

假设旋转破坏机制外的土体是刚性土体，锚杆剪应力和锚杆与土体的相对位移即锚杆变形存在以下关系：

其中：表示锚杆相对土体位移；是锚杆−土界面单位位移剪切强度；τ表示锚杆极限抗剪强度。

而锚杆的轴向应力与轴向应变存在以下关系：

式中：为锚杆的弹性模量；ε为锚杆的轴向应变。

根据材料力学可知，锚杆轴向应变与锚杆的相对位移存在以下关系：

所以，锚杆轴向应力通过水平方向求导可 得到：

结合式(7)～(11)，可以化简得到以下表达式：

通过数学关系可以求得锚杆在水平方向上的相对位移关系式：

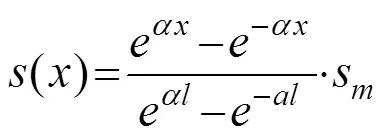
因此，锚杆的轴力也可通过相对位移计算得到，如下所示：

单个锚杆做功速率也可以通过锚杆的轴力沿水平方向积分得到，如下所示：

4 安全系数求解

根据极限分析上限理论，隧道掌子面的稳定条件是外力做功功率小于内部耗散率，即

式中：P表示外力做功功率；P表示内部耗散率。

在本文提出的机制中，需要考虑的外力做功有重力及锚杆做功，因此外力做功功率为：

式中：P表示重力做功功率；P表示锚杆做功功率。

重力做功功率可分2部分计算获得。第1部分土体重力做功功率1表达式如下：

第2部分土体重力做功功率2表达式如下：

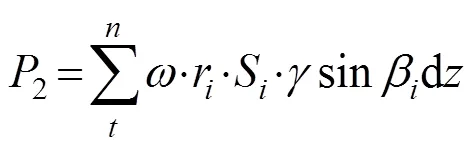
锚杆做功功率为：

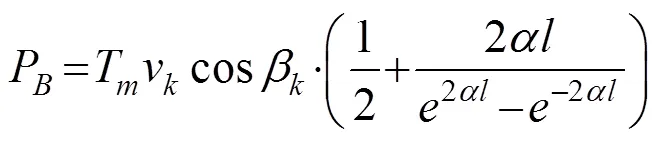
土体内部耗散率为：

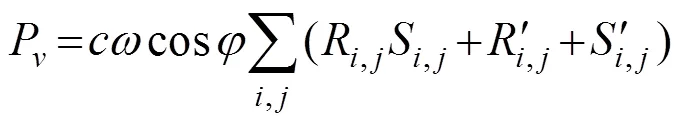
根据极限分析上限法，可得隧道掌子面安全系数可表示为下式：

需要注意式(24)中的极限支护压力的计算过程是利用非线性最小优化算法fminsearch通过对所构建模型的参数r/D，β和进行优化来获得计算公式的最大值，即为所得安全系数。

5 结果验证

本节对本文所提出破坏模型计算获得的安全系数与PAN等[7]计算结果进行比较，以一开挖面积为100 m2，直径约为11.28 m的隧道进行验证。具体参数见表1。

通过非线性最小优化算法fminsearch优化计算获得的破坏机制交叉层部分见图10，将计算获得的安全系数与PAN等[7]获得的结果进行对比，见图11。图11给出了锚杆密度为0.25根/m2和0.5 根/m22种情况下的结果对比。

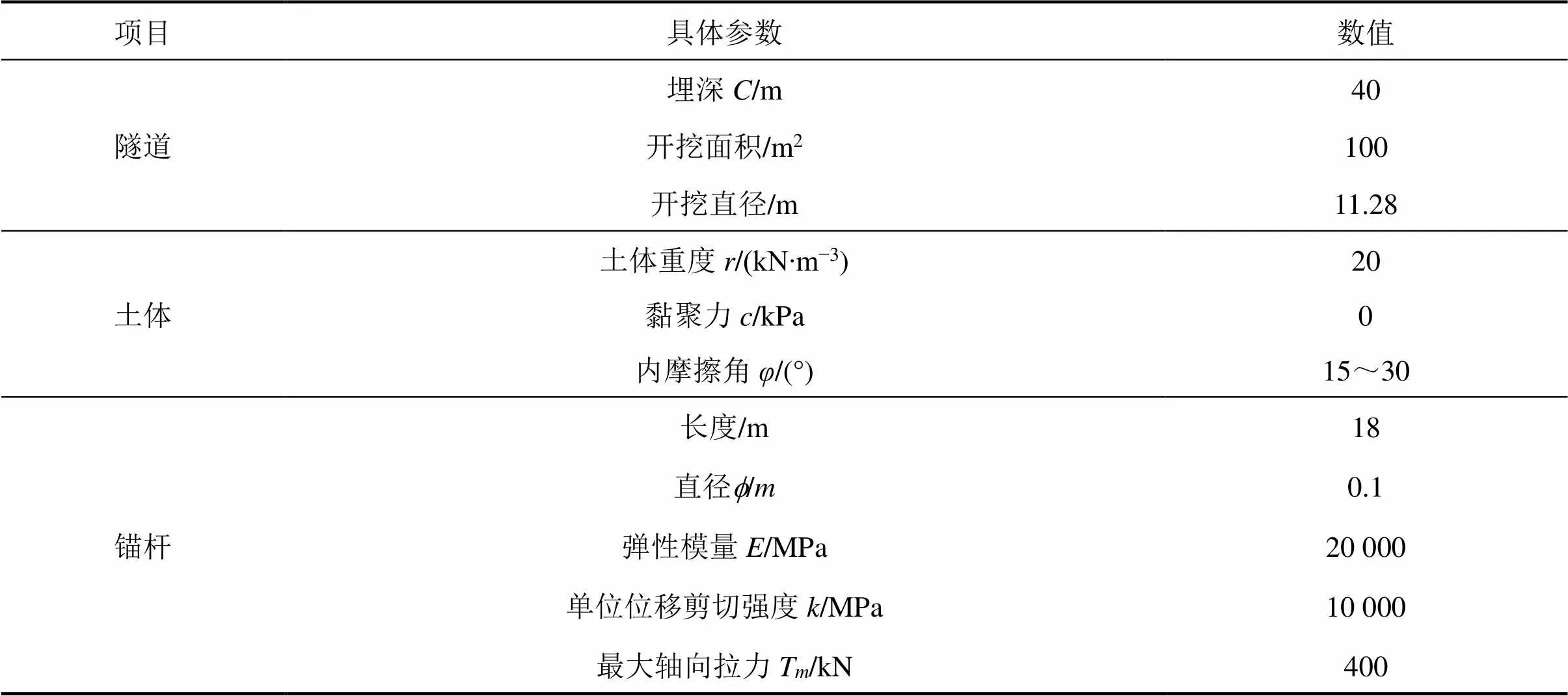
表1 隧道、土体及锚杆参数

图11 本文获得安全系数与PAN结果比较

由图11可知，本文所提出模型总体上与PAN等[7]的结果极为接近，说明本文的模型是可靠的。本文所提出方法计算获得的安全系数随着内摩擦角的增大更为快速的增大，原因是本文考虑了砂性土的拱效应，采用普氏压力拱理论计算隧道覆盖层的坍塌土体做功，受内摩擦角的变化影响较大，进一步说明本文推导的模型更加适用于砂土隧道的掌子面稳定性分析。

6 工程应用

将本文所提出方法应用到新建的太达村隧道DK241+790断面，该隧道埋深15 m，该断面处0～5 m处岩土摩擦角为25°，5～15 m处岩土摩擦角为32°。采用本文所提出对该断面处加固掌子面稳定性进行分析，该隧道断面简化为等面积圆(=11.3 m)。加固示意图见图12。采用本文所提出方法并采用图12加固方案获得的安全系数为1.8＞1.0，说明该加固方法能够保证隧道掌子面稳定。按照图12进行锚杆注浆加固现场施工(见图13)。图14表示的是监测到的地表稳定后的沉降曲线图。

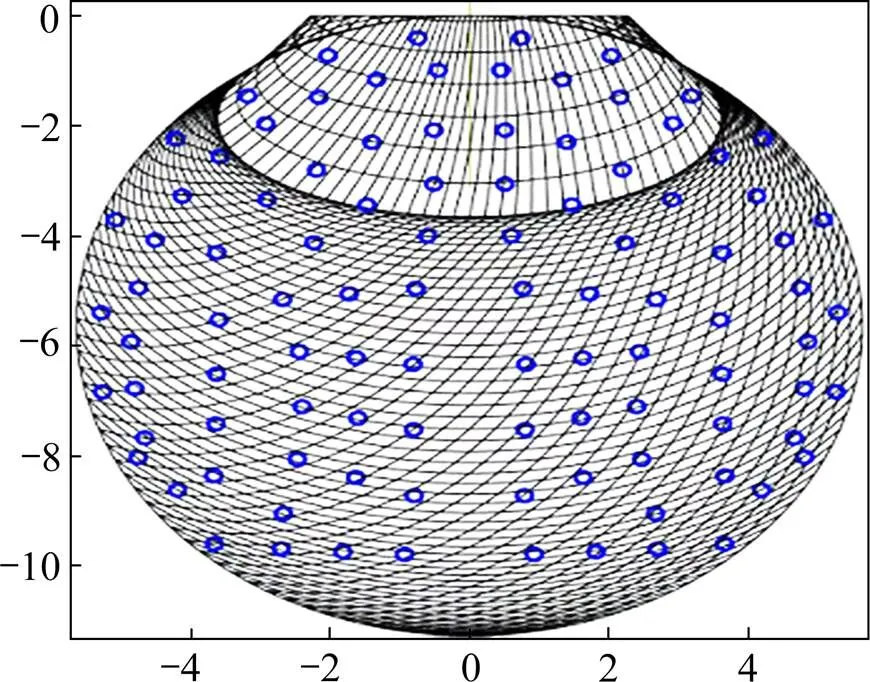
图12 破坏机制及锚杆布置

图13 锚杆注浆现场

从图14可得，该断面经过锚杆加固后满足掌子面稳定性要求(最大地表沉降小于30 mm)，说明本文所提出方法能够准确地评估砂土隧道锚杆加固掌子面稳定性，能够有效指导太达村隧道砂土段隧道掌子面加固设计和施工。

图14 地表沉降曲线

7 结论

1) 基于所提出的砂土隧道掌子面破坏机制，建立了砂土隧道掌子面锚杆支护分析模型，分析了砂土隧道在锚杆支护下掌子面的稳定性，并与PAN 等[7]的结果进行比较，结果表明本文的模型计算结果是可靠的，且更适合砂土隧道掌子面稳定性 分析。

2) 通过结合具体的工程，可知本文所提出方法能够有效指导实际隧道工程砂土段隧道掌子面加固设计和施工。

[1] 王志杰, 吴凡, 王如磊, 等. 深埋风积沙地层隧道掌子面失稳特征研究[J]. 铁道工程学报, 2020, 37(1): 85−92. WANG Zhijie, WU Fan, WANG Rulei, et al. Research on the instability characteristics of the tunnel face in deep-buried aeolian sand stratum[J]. Journal of Railway Engineering Society, 2020, 37(1): 85−92.

[2] QIAN Z, ZOU J, PAN Q, et al. Safety factor calculations of a tunnel face reinforced with umbrella pipes: A comparison analysis[J]. Engineering Structures, 2019(199): 109639.

[3] 王克忠, 朱海斌, 孔令民, 等. 新意法在野猪山隧道施工中的应用研究[J]. 浙江工业大学学报, 2017(3): 62−69. WANG Kezhong, ZHU Haibin, KONG Lingmin, et al. An application study on the ADECO-RS approach in the construction of Yezhu mountain tunnel[J]. Journal of Zhejiang University of Technology, 2017(3): 62−69.

[4] Yoo C, Shin H K. Deformation behaviour of tunnel face reinforced with longitudinal pipes-laboratory and numerical investigation[J]. Tunnelling & Underground Space Technology, 2003, 18(4): 303−319.

[5] Peila D. A theoretical study of reinforcement influence on the stability of a tunnel face[J]. Geotechnical & Geological Engineering, 1994, 12(3): 145−168.

[6] 周捷, 席锦州, 漆泰岳. 纤维锚杆预加固在大断面隧道中的应用研究[J]. 公路隧道, 2016(4): 32−39. ZHOU Jie, XI Jinzhou, QI Taiyue. Application of fiber anchor pre reinforcement in large section tunnel[J]. Road Tunnel, 2016(4): 32−39.

[7] PAN Q, Dias D. Safety factor assessment of a tunnel face reinforced by horizontal dowels[J]. Engineering Structures, 2017(142): 56−66.

[8] Mollon G, Dias D, Soubra A H. Rotational failure mechanisms for the face stability analysis of tunnels driven by a pressurized shield[J]. International Journal for Numerical & Analytical Methods in Geomechanics, 2011, 35(12): 1363−1388.

[9] CHEN G H, ZOU J F, QIAN Z H. An improved collapse analysis mechanism for the face stability of shield tunnel in layered soils[J]. Geomechanics and Engineering, 2019, 17(1): 97−107.

[10] ZOU J F, QIAN Z H, XIANG X H, et al. Face stability of a tunnel excavated in saturated nonhomogeneous soils[J]. Tunnelling and Underground Space Technology, 2019, 83(Suppl): 1−17.

Assessment of the reinforced tunnel face stability in sand soils

HE Zuo, YANG Dong, CHEN Dun, LIU Zhiqiang, ZHANG Jinlong,ZHENG Jiayong, SUN Liwu, CHENG Jie

(China Railway 18th Bureau Group Fifth Engineering Co., Ltd., Tianjin 300451, China)

For the Taidacun tunnel of Yumo railway, combined with theory of Proctodyakonov’s pressure arch and the three-dimensional rotational failure mechanism, an improved three-dimensional rotational failure model with considering soil arching effect was proposed to investigate the tunnel face stability in sand soils. The proposed failure mechanism could be divided into two parts: (1) the rotational failure part in the crossed layer; (2) the arching failure part in the cover layer. Based on the proposed failure mechanism, the soil-anchor model was used to study the stability of reinforced tunnel faces. The results show that: (1) compared with the existing research results, the proposed method is reliable and more suitable for the stability analysis of tunnel faces in sand soils; (2) Combined with the practical tunnel engineering, it can be seen that the method proposed in this study can effectively guide the design and construction of tunnel face reinforcement in sandy soils.

Proctodyakonov’s pressure arch; soil arching effect; tunnel face stability; soil-anchor model; safety factor

U45

A

1672 − 7029(2021)02 − 0468 − 08

10.19713/j.cnki.43−1423/u.T20200989

2020−10−22

贵州省科技重大专项资助项目(黔科合重大专项[2018]3010)

贺祚(1985−)，男，天津滨海新区人，高级工程师，从事铁路工程施工技术管理及研究工作；E−mail：34477654@qq.com

(编辑 蒋学东)