基于经验模态分解的斜拉桥拉索索力异常检测
李远棣
(1.桂林理工大学 土木与建筑工程学院,广西 桂林 541004;2.广西岩土力学与工程重点实验室,广西 桂林 541004)
斜拉索是斜拉桥的主要承重构件,也是薄弱环节.索力的变化能反映出拉索的状态,也可反映出桥梁结构整体的内力变化状态,因此在斜拉桥运营期间,应对拉索索力进行监测和评估[1-2].很多斜拉桥都建有健康监测系统,能监测拉索的实时索力[3].检测异常索力时,常用单根拉索索力的偏差值作为评估指标,当偏差值大于一定范围(如10%)时,即判定索力可能处于异常状态.该评估方法缺乏严格的理论支撑,检测不到小范围的异常变化.针对斜拉索的状态评估还有安全系数法、可靠度理论、变权综合法、灰色关联度等方法[4-7].这些研究从多个方面改善了拉索的状态评估,但是对于桥梁健康监测系统的实测索力并不能很好地识别出异常.
为了提高索力异常检测的准确度,本文将经验模态分解方法应用于索力异常监测中,结合实测数据和模拟出的异常数据,确定最优的固有模态函数计算阶数和异常判断阈值.通过对拉索实测索力的分析,研究其在长时间和短时间内的变化趋势,使用经验模态分解法去除索力数据的外在干扰因素,设定合理阈值,检测斜拉桥拉索的异常索力.以衡阳东洲湘江大桥健康监测系统实测索力数据为例,进行异常检测,本文所提方法准确识别出了索力异常.
1 经验模态分解异常检测方法
1.1 经验模态分解法原理
经验模态分解法(Empirical Mode Decomposition,简称EMD)是一种自适应信号分解方法,能够很好地处理非线性非平稳数据序列[8].该方法假设任何复杂的信号都是由一系列简单且相互独立的固有模态函数(Intrinsic Mode Function,简称IMF)组成,所有信号都可以分解为数个本征模态函数(IMF)与1个余量rn(t)之和.
IMF视为信号中的振动成分,反映了信号中不同频率成分,频率逐渐降低,余量为信号中的趋势项.把监测索力信号输入,会计算出数个IMF序列;对序列进行分析,选出能够反映拉索索力自身变化的数据项和干扰趋势项,最终在监测数据中去除干扰因素变化,然后再检测异常变化.
1.2 EMD算法计算过程
1) 输入信号y(t),确定信号中的极大值点和极小值点,运用三次样条插值方法获得上包络线u(t)和下包络线d(t),计算出平均包络值m(t),即
(1)
2) 原始信号减去平均值包络值m(t)得到第一向量h(t),即
h(t)=y(t)-m(t).
(2)
3) 判断h(t)是否满足IMF条件,若满足,则h(t)为IMF;若不满足,将h(t)作为新的输入信号,重复上述步骤1)~2),直到得出符合要求的IMF,称作第1阶本征模态函数,记为IMF1.
4) 原始信号减去本征模态函数得到r(t),把r(t)作为输入信号,重复步骤1)~3),得到IMF2.
r(t)=y(t)-IMF1.
(3)
5) 重复步骤1)~4)得到满足要求的余项rn(t),终止循环.通过上述循环计算可得n个IMF数据和1个余项rn(t),令ci(t)=IMFi,那么原始数据可表示为
(4)
式中:rn(t)为外界干扰因素(温度、天气等)产生的索力变化数据.
把拉索索力监测数据作为输入项y(t),按以上过程计算,得到的IMFi即为斜拉桥自身状态产生的索力变化数据,可进行异常检测.
1.3 阶数的选取
计算得到的数个IMFi序列频率变化并不相同,阶数越高频率越低.对索力进行异常识别时,不同阶数的模态函数IMF所代表的震动波形也各不相同,想要得到拉索去除干扰后的震动信号,应对索力变化特征作具体分析选定合适的阶数.以如图1所示的实测索力数据为例,把一些数据点作增大处理,用来模拟实际运营时的异常索力,用EMD法计算的结果如图2所示.
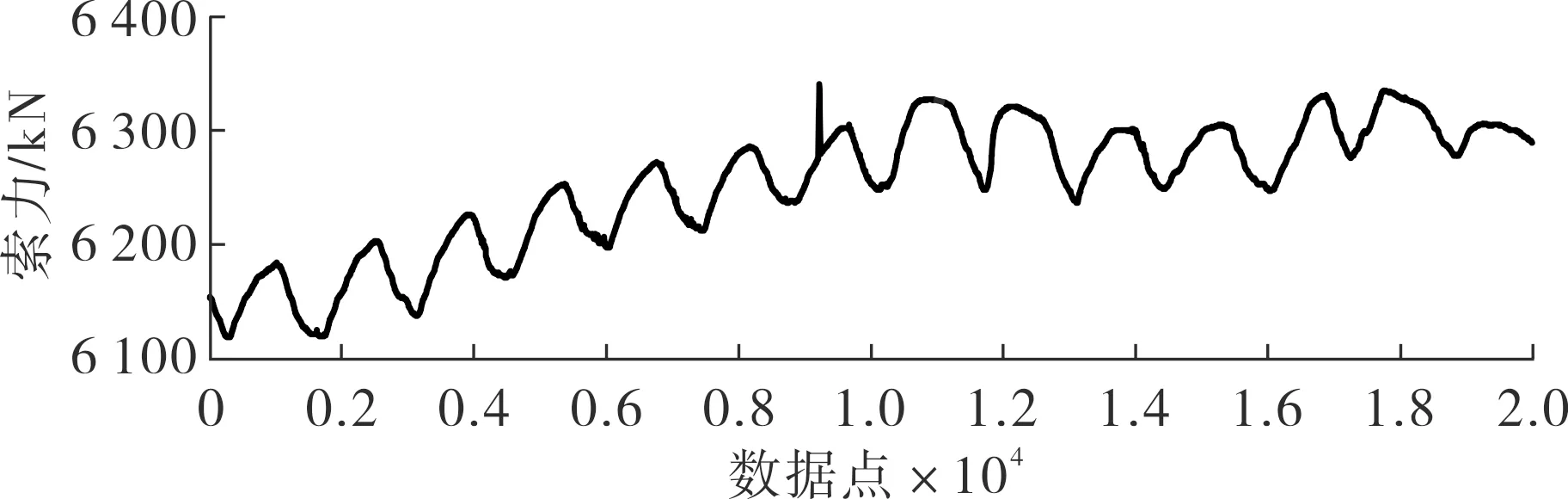
图1 索力数据
由图2可以看出:索力原始信号经EMD算法处理后,共得到12个IMF函数和1个余项;前3阶振幅较小,震动变化频率较大,后面震动幅度开始变大;从第8阶开始,信号发生显著变化,振幅大幅加大,震动频率明显降低;且从第8阶开始索力原始信号的异常处在IMF函数图中不再显示,前7阶在异常位置均有显示,第7阶异常信号有所发散.
定义IMF函数震动波形开始出现显著变化,且波形中不显示异常信号(如图2所示的第8阶IMF函数)时的阶数为发散阶数.从桥梁健康监测系统(详情见2.1节)中抽取50组实测索力数据样本,每组样本包含5 000个数据点,并把样本中的一些数据点随机增大或减小(1%~5%),模拟实际异常信号,代入EMD算法处理,分析IMF函数开始发散的阶数,结果见表1.

表1 IMF函数发散阶数统计
由表1可以看出:发散阶数为7阶或8阶的测试样本占84%,小于7阶的仅有1次,余下为9阶或10阶.在实际测试中还发现:在发散阶数的前一阶虽然能测出异常信号,但在异常位置出现噪声干扰(如图3所示的IMF7函数),会对异常位置的判断产生不良影响.
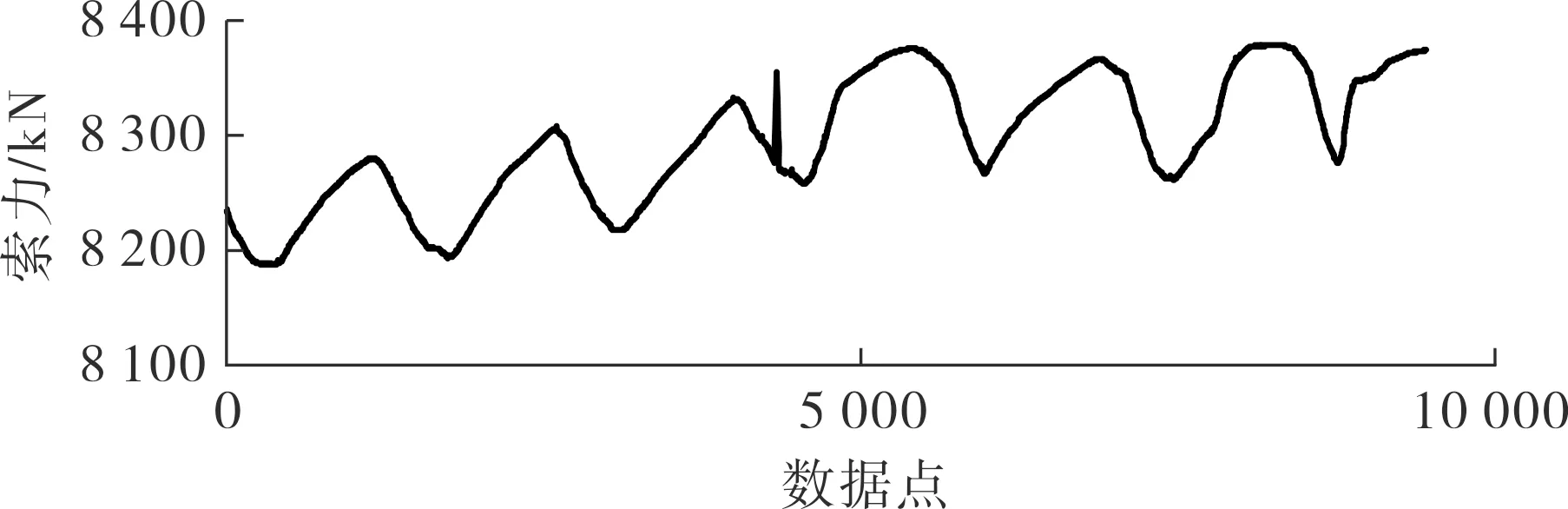
(a) 原始信号
综上所述,选取前5阶模态函数作为分析数据检测异常,后面的函数作为趋势项进行索力的EMD算法计算时,得出5阶IMF函数即终止运算,可有效减小计算量,加快检测速度.设F(t)为去除外界影响(主要是温度)后的索力分析数据,Y(t)为监测系统实测索力数据,R(t)为索力变化趋势,则有
Y(t)=F(t)+R(t),
(5)

(6)
使用式(6)计算出F(t),把F(t)作为新索力信号进行分析,如图3所示.结果表明:EMD算法可显著增大异常索力的敏感度,使用前5阶IMF函数完全能够识别异样点,增加异常检测的准确度.
1.4 阈值设定
由图3可以看出:斜拉桥健康系统实测数据经过EMD计算,分离出趋势项和去除干扰数据后,数据信号在异常处剧烈波动,其他位置呈现波动很小的随机变化,整体沿y=0呈对称形态.依据这些特征,设阈值为L,当索力异常时有
F(t)≥Lu或≤Ld,
(7)
式中:Lu、Ld分别为上阈值和下阈值.
Lu/d=u±3σ,
(8)
式中:u为F(t)信号样本的均值;σ为F(t)信号样本的标准差.
斜拉桥设计使用年限长久,长期运营下索力也会出现变化,可以每隔一段时间调取最新监测数据,更新异常判断条件中的上下阈值,保证长期异常检测的准确性.
1.5 检测流程
检测开始前要先从监测系统中提取出一定时间内的索力数据Y,经EMD计算,使用式(6)得到F信号样本,再依据式(8)得到上下阈值Lu和Ld.具体的检测流程如下:
1) 输入监测系统实测索力信号Y(t);
2) 用EMD算法处理数据,得到前5阶IMF函数,使用式(6)计算去除干扰后的索力数据F(t);
3) 把式(7)作为索力异常判别条件,当F(t)≥Lu或者F(t)≤Ld时,认定索力出现异常;
4) 若索力出现异常则发出预警,结合实际情况对异常出现位置进一步分析,若没有异常则返回步骤1)继续检测.
2 实例计算分析
2.1 工程概述
衡阳东洲湘江大桥位于雁峰区和珠晖区交界处,是衡阳市南部重要的过江通道.主桥为三塔单索面双排索混凝土矮塔斜拉桥,跨度120 m+2×210 m+120 m,主塔高35 m.斜拉索采用单丝涂覆环氧喷涂钢绞线,单根钢绞线直径为15.2 mm,全桥共有96根拉索,布置类型为单索面双排索,固定于道路中央的分隔带处,整体情况见图4.

图4 衡阳东洲湘江大桥
为保障施工和运营的安全,该桥建有健康监测系统,对拉索索力进行监测.应用了智能光纤光栅监测方案,有21根拉索内置索力传感器,可长期监测拉索索力.
2.2 索力异常检测
先从桥梁健康监测系统中抽取2019-07-01—08-31共2个月的实测索力数据,对其作EMD计算,依据式(8)得出索力的上下阈值Lu和Ld.全桥共有21根拉索采集有效的监测数据,拉索的位置和受力情况各不相同,依照上述方式,得出每根拉索对应的阈值,具体计算结果见表2.

表2 阈值计算结果
按照2.4节所述检测流程,对2019-09—2020-06的监测数据进行EMD计算,检测异常点,结果见表3.由表3可以看出:拉索检测出的异常次数在9~15次之间,偏差率均在5%以下.以S01和S18拉索为例,检测出拉索在2019-09-04—06时间段产生了多次异常,提取当时的索力数据(见图5),进一步分析索力的异常变化.结合索力实测数据可知,在此期间索力确实出现了异常波动.查阅桥梁建设资料得知,在该时间段内东洲湘江大桥进行了成桥静载试验,引起索力的异常变化.
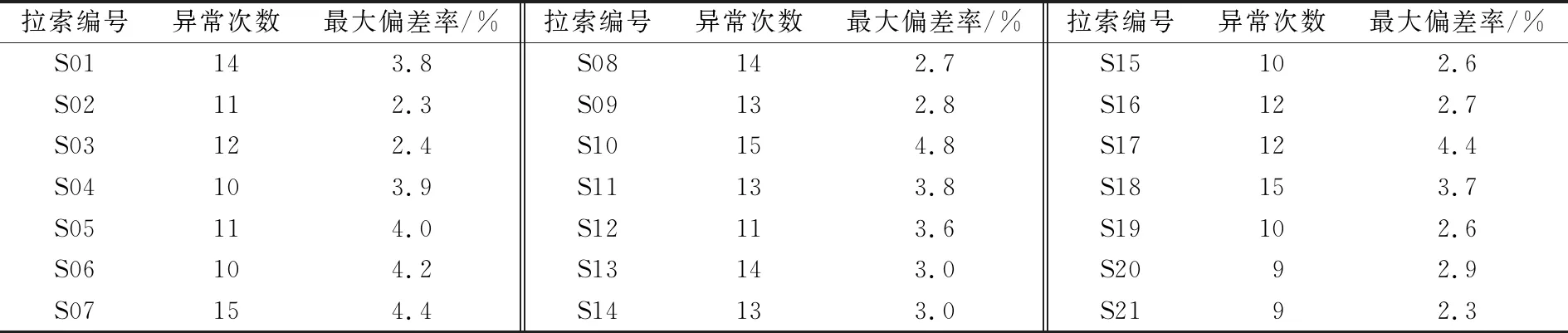
表3 异常检测结果
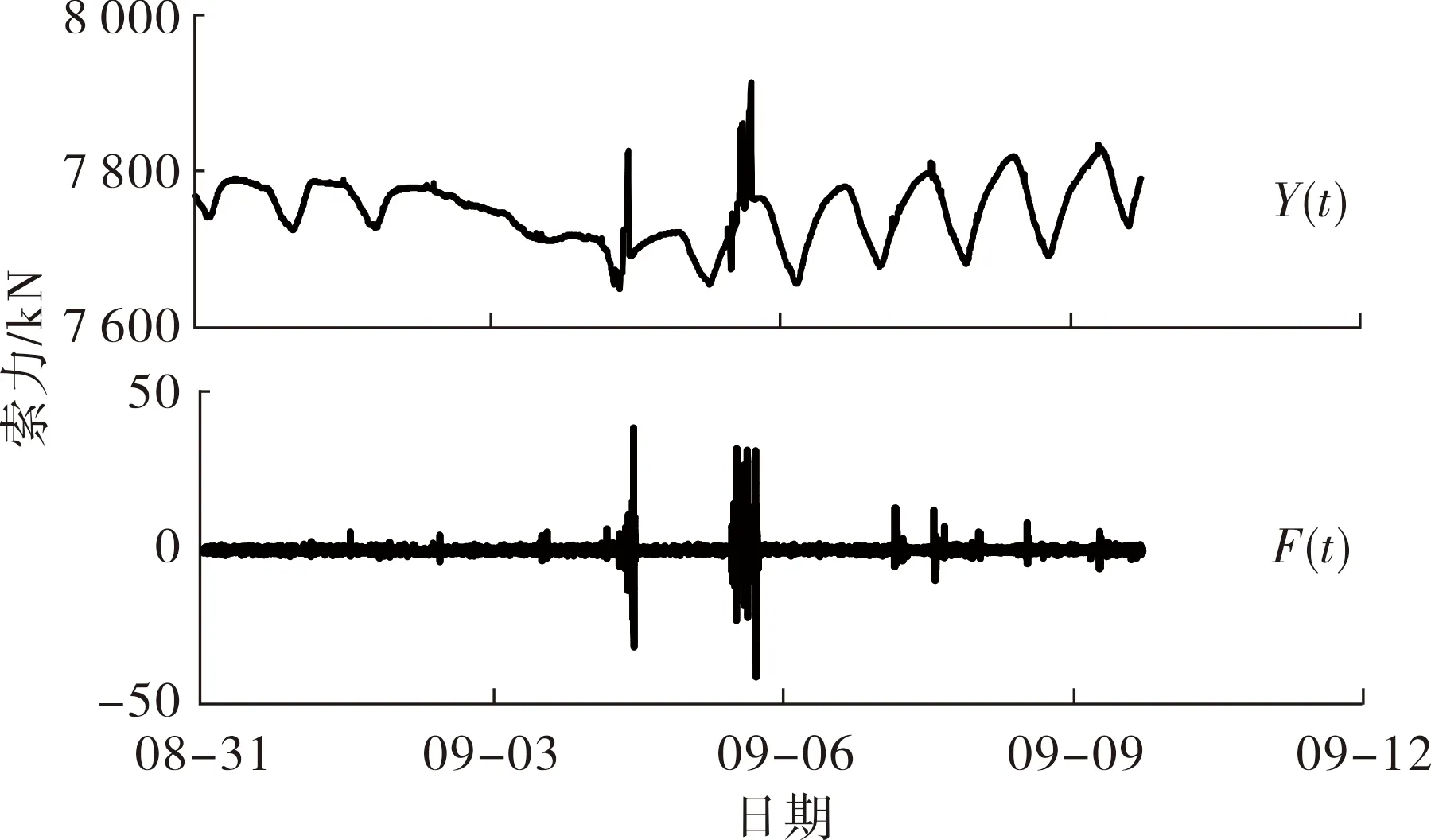
(a) S01
3 结论
1) 经验模态分解法(EMD)能够把健康监测系统测得的原始索力数据分解为数个不同的固有模态函数(IMF),选定适当阶数的固有模态函数组成新的数据可以去除干扰因素,突出异常点.
2) 对衡阳东洲湘江大桥健康监测系统实测索力数据,进行基于经验模态分解的拉索索力异常检测.结果表明,该方法抗干扰能力强,索力异常识别精度高.
3) 本文所提方法理论简单易于实现,可用于斜拉桥健康监测系统中实现实时索力数据异常检测.但异常检测方法中的参数和阈值都是依据东洲桥的监测数据而设置,因此用于其他斜拉桥的索力异常检测时还需进一步验证或调整.

