结合模糊控制的时序数据预测循环神经网络

田贤忠，顾思义，胡安娜

(浙江工业大学 计算机科学与技术学院，杭州 310000)

1 引 言

当代社会的各个领域中，每时每刻都会产生海量的时序数据，例如，金融、气象、交通和医疗等.高效的对这些时序数据进行处理和分析，能够让人把握事件的趋势，做出更好的决策.

使用循环神经网络(Recurrent Neural Network,RNN)来处理时序数据是一种有效的方法，其中长短期记忆(Long-Short Time Memory，LSTM)[1]网络和门控循环单元(Gated Recurrent Unit，GRU)[2]网络是最常用的两种RNN的变体，解决了RNN中梯度爆炸和梯度消失的问题.在交通领域，Fu R等人使用了LSTM和GRU对交通流量数据进行预测[3]；在工业领域，Zhao R等人将GRU使用于机器设备的健康监测[4]；在医疗领域，Choi E，Ruan T等人使用GRU训练了电子健康档案数据，预测病人未来的健康状况[5，6]，Che Z等人则考虑到了医疗数据中时序数据采样不均的问题，使用了改进结构的GRU模型进行训练[7]；在语音语义识别中，冯诗影等人对循环神经网络运用在语音识别中，并对训练过程优化，明显提高了模型训练效率[8]，李永帅等人构建了一个双向的LSTM多层网络模型，克服了传统情感词典中情感词倾向不变形等问题[9]；在时序数据预测任务中，张旭东等人设计了一种LSTM模型，可以使网络训练与人的经验知识结合，使训练过程更有目的性[10].

早在1996年，Chen P等人发现宏观和金融指数色混沌的广泛证据，证明经济体运动是高度复杂的非线性运动，不是随机过程[11].因此，金融系统走势也是可以被预测的，许多研究都选择使用机器学习来对金融市场走势进行预测.Fengmei Y 等人混合了多种机器学习方法[12]，对中国股市进行预测并自动作出决策，Kai Chen等人使用LSTM预测了中国股市的回报[13]，Sreelekshmy S等人比较了LSTM，RNN和滑动窗口的CNN在股市预测中的表现[14]，Qin Y等人提出了双阶段注意力机制循环神经网络模型，预测了纳斯达克100的股票价格[15]，Hajiabotorabi Z等人使用RNN变种来对变化较快的高频交易数据进行预测[16]，Yeqi L等人提出了一种RNN的改进结构，增强了RNN的时空关联，并运用于金融市场的预测中[17].

虽然RNN能在大多数时序数据处理任务上有较好的表现，但是目前并没有合适的RNN模型是针对金融时序数据的特点的.首先，金融数据仅仅会在工作日产生，在周末以及节假日，不会有新的数据产生，因此时间序列时间间隔是非等的；其次，金融系统的市场稳定程度也会影响系统后续的趋势.由于金融数据中的时间序列非等并不是由于数据缺失，因此当前RNN模型主要用于处理这类问题的插值法并不适用，而市场的稳定程度这一信息在RNN模型中也不能高效的被利用.

针对上述RNN模型在处理金融时序数据时问题，本文基于GRU模型结合模糊控制提出了一种新的网络模型——GRU-F(GRU-Fuzzy).GRU-F的特点如下：1)能够解决金融时序数据中时间间隔非等的问题；2)通过模糊控制的结构来利用金融数据中市场稳定程度的信息.

2 背景知识

2.1 门限循环单元GRU

GRU模型[2]是RNN模型的变体，可以用于时序数据处理.RNN模型认为输入(包括输出)之间不是相互独立的.它可以实现神经元参数共享，即网络当前时刻的神经元训练参数可以在接下来的过程中被使用，所以网络在序列上可以保存历史的状态信息，适合用于训练有序序列数据.由于RNN模型在一个时间窗口中共享了神经元参数，因此可以大幅减少模型中需要学习的参数数量.GRU模型在RNN的基础上增加了2个门结构，用于解决RNN中的长期依赖问题.

GRU模型结构为图1所示.at为网络输入，ht为记忆层的输入输出，它既是上一记忆层的输出，也是下一记忆层的输入.这种结构继承了RNN模型的特性，共享了神经元参数.GRU的重置门rt，更新门zt控制每一时间步上的记忆层的更新.模型的前向传播公式如下：

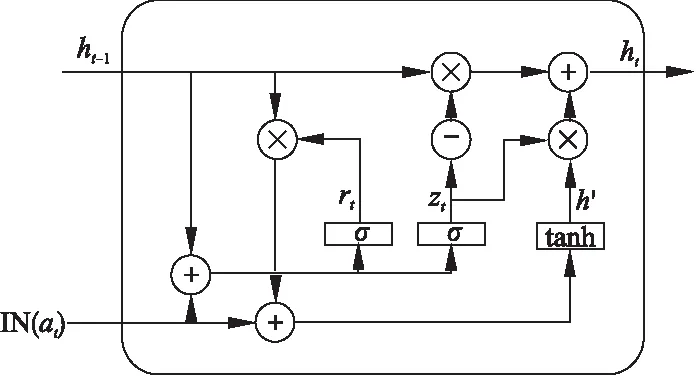
图1 GRU模型结构Fig.1 Structure of GRU

rt=σ(Wrat+Urht-1+br)

(1)

zt=σ(Wzat+Uzht-1+bz)

(2)

h′t=tanh(Wat+U(rt⊙ht-1)+b)

(3)

(4)

其中矩阵Wr,Wz,W和向量br,bz,b是模型参数，分别表示连接权值矩阵和偏置值.本文使用σ(v)代表向量中逐元素进行Sigmoid函数运算，⊙是逐元素相乘的运算符.

GRU模型的局限性在于，模型不能很好的处理时间间隔不等的时序数据，相邻的两层之间时间间隔变化时，这种变化无法很好的在模型中体现.

2.2 模糊控制

模糊控制是以模糊集理论、模糊语言变量和模糊逻辑推理为基础的一种智能控制方法[18]，它是从行为上模仿人的模糊推理和决策过程的一种智能控制方法.模糊控制适用于有模糊环境且难以建模的控制系统.模糊控制器的基本结构如图2所示.

图2 模糊控制器Fig.2 Fuzzy controller

模糊化是将系统中的精确量转化到模糊集合中；模糊规则是根据经验建立模糊规则库，实现基于知识的推理决策；去模糊化则将推理得到的控制量转化为控制输出.

通过模糊控制器使记忆层在保留信息的过程中能够对当前数据的波动水平有自适应调整.

3 使用模糊控制的非等间隔时序循环神经网络模型

本文提出了一种使用模糊控制的时间序列循环神经网络模型——模糊循环GRU神经网络(GRU-F).其基本思想是：改进GRU模型的结构，在t-1时刻的记忆层传递到t时刻时增加一个模糊控制结构，使其能够更合理的处理时间间隔不等的时间序列.模糊控制结构能够根据t时刻之前的信息和t时刻到t-1时刻的间隔决定记忆层有多少信息从t-1时刻保留到t时刻.具体的网络模型由图3所示.

图3 由GRU-F组成的网络模型Fig.3 Network model consists of GRU-F

3.1 模型的输入与输出

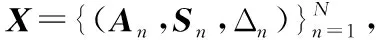
1)A是一个D维长度为M的数据序列

A=[a1,a2,a3,…,aM]T∈M×D

2)一个大小与A相同的序列S

S=[s1,s2,s3,…,sM]T∈M×D

3)一个长度为T的序列Δ

Δ=[δ1,δ2,δ3,…,δM]T

其中δt为t时刻数据与t-1时刻数据的时间间隔.

每个输入(An,Sn,Δn)，GRU-F模型单输出一个K维的向量Y，

Y=[y1,y2,y3,…,yk]

其中，yk表示当前输入经过模型后得到的结果在维度k上的值.当K=1时，模型的输出一个预测值.

3.2 GRU-F单元结构

金融市场产生的数据，由于在节假日不会有市场不会产生交易，不会有新的数据产生，因此金融数据中的时间间隔是不固定的.例如，普通工作日市场的相邻两个数据之间间隔为1天，而每逢周末，相邻两个数据之间的间隔为3天，在节假日这个间隙会更大.数据中的时间间隔是影响金融市场走势的一个重要因素.除此之外，市场的波动水平也是影响市场走势的一个重要因素.因此，一个能够很好的处理市场不规律的时间间隔和市场波动水平两个信息的单元结构可以提高预测性能.

GRU-F的网络结构如图4所示.在记忆层的信息进入下个记忆层之前，会通过一个完全由输入驱动的分解网络，该结构可以根据时间间隔和市场波动水平控制记忆层记忆多少信息进入下一层.相对于较小的时间间隔，时间间隔较大时记忆层将遗忘更多的信息；相对于较小的市场波动，市场波动较大时记忆层也将遗忘更多的信息.其具体结构如下：

图4 GRU-F单元结构Fig.4 Structure of GRU-F

(5)

(6)

g(δt,st)=lapse(δt)·fuzzy(st)

(7)

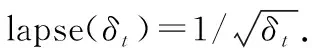
fuzzy(st)为一个单变量二维模糊控制器.根据st记录的数据中每个维度的当前波动的程度，控制记忆层中信息衰减程度.输入变量的模糊集论域计算出st的范围，输出变量的论域为(0,1].模糊化过程的隶属度函数选择三角形隶属度.输入变量和输出变量的模糊子集均为{NB,NS,ZE,PS,PB}.去模糊化的过程本文使用直观且运算量小的重心法.

(8)

(9)

(10)

(11)

其中，at是当前时刻的输入，参数{Wr,Ur,br}，{Wz,Uz,bz}，{W,U,b}分别是重置门、更新门和候选集的网络参数.σ(·)是向量中逐个元素的Sigmoid(x)计算:

(12)

最后，ht经过输出层得到输出，

Ot=f(Woht)

(13)

以上的合计决定了数据的时间间隔和数据波动水平会影响记忆层保留多少信息到下一层.使模型更合理的处理金融时序数据.

3.3 模型的训练

GRU-F是一个平滑的、相互连接的模型，模型是可微的，因此，本文采用了反向传播(BPTT)的算法对模型参数进行更新.

本文采用batch技术，使网络能够更好的收敛.训练时，从样本池中按顺序选取batch-size数量的样本进行训练，batch的规模默认为32.另一方面，根据网络输出值和目标值之间的差值的平方，即均方误差(Mean Squared Error，MSE)为目标函数函数，即:

(14)

其中，N代表总样本数，targett代表了t时刻的样本的实际观测值，predictedt代表了t时刻样本的网络预测值.训练使用Adam优化器更新网络参数.

GRU-F模型架构的完整训练过程如表1所示.

表1 模型的训练过程Table 1 Training process of the model

4 实 验

本文通过实验，验证GRU-F模型的性能.实验环境均为Python 3.6，Windows10 64位系统，64G内存，CPU i9-9820X，显卡NVIDA 2080Ti显存11G，TensorFlow的版本为1.12.

4.1 数据准备与预处理

数据使用美股S&P500中选取的25支股票与上证50中选取的25支股票近10年的日线数据，包括了每只股票每日的开盘价，最高价，最低价，收盘价，成交量数据，以及通过以上基础数据计算出的RSV，KDJ，AR，BR，ASI，ROC，RSI，W&R指标，组成特征数据集.

通过滑动窗口将M个交易日的数据作为一组输入数据，第M+1个交易日的收盘价作为输出对数据进行分组，生成训练数输入据集X和输出数据集Γ.

由于股市中各指标数据通常数值较大，且单位不同，不适用于模型，所以为了使数据适合GRU-F计算，并且一定程度上消除量纲的影响，本文对数据进行归一化操作得到A∈M×D.对于长度为M的窗口任意维度的数据，使用tanh函数进行归一化处理：

(15)

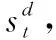
按照70%的训练集、15%的验证集和15%的测试集划分.输出层使用大小为64的Linear层，使用Dropout设置为0.2防止过拟合，Batch-Size为32.

4.2 参数设定与评估标准

GRU-F有3个参数需要设置，时间窗口长度M，记忆层的大小h，波动水平侦测参数l.为了确定M和l的值，本文使用网格搜索，并且为了简化，将其设定为M=l，M=l∈{5,10,15,30}，通过实验得出当M=15时，模型表现最佳；确定h的值，h∈{16,32,64,128,256}，实验得出当h=32, 64时，模型表现最佳，实验结果如图5所示.同时，我们发现，我们的GRU-F模型有着更好的鲁棒性.为了评估各个模型的性能，使用绝对平均误差(MAE).

图5 各个模型不同的记忆层规模在上证50中的平均MAEFig.5 Average MAE of different hidden layer sizes of each model in SSE 50

4.3 模型训练对比

本文以苹果(AAPL.US)的数据为例，预测次日收盘价.将GRU-F模型训练过程与Attention-RNN和GRU进行对比.在Attention-RNN和GRU模型中，时间间隔仅作为一个普通的输入数据来处理.可见本文提出的GRU-F的效果更好.实验中，如图6所示，GRU-F的Epoch在150左右时已经有较好的结果，继续训练测试集上的精度不再上升.

图6 Att-RNN，GRU和GRU-F训练过程对比Fig.6 Comparison of Att-RNN,GRU and GRU-F training process

4.4 结果分析

本文对数据集中所有的50支股票进行测试，对比使用不同方法得出的预测结果，包括ARIMA[19]，GRU，Attention-RNN[20]，DA-RNN[15]记忆层规模在32和64时.评估结果如表2所示.

由于GRU-F能够更好的处理数据中的非等的时间间隔和数据的稳定程度，如表2所示，GRU-F的表现最好.而ARIMA预测模型依赖数据的稳定性，因此在股市上的表现略差.结果中还可以看出，模型在上证股票中的表现要好于S&P500，这可能是由于中国股市每日的波动会被控制在10%以内，而美股的股价完全自由，波动范围更大.

表2 模型在美股和A股市场中性能评估Table 2 Performance evaluation of the model in S&P500 and SEE50

5 结束语

时序数据预测的问题一直存在于社会生产中，利用机器学习处理数据可以消除人的主管干扰.针对不同生产环境数据的特点，使用或者改进相应的机器学习模型，能够得到更好的结果.本文提出了一种GRU-F的网络模型，针对金融市场中的时序数据的特点对GRU模型进行了改进.一方面，模型改进后能够处理金融数据中的非等时间间隔；另一方面，模型能够更好的利用当前市场波动程度的信息，提高模型预测精度.最后，对于金融数据的特点如何使模型预测精度更高是未来研究的方向.