《椭圆的标准方程》教学设计

课程分析：

《椭圆的标准方程》是高中人教版B版选修性必修一第二章第5节2.5.1中的内容。继直线和圆的方程之后，《椭圆的标准方程》拉开了圆锥曲线与方程的序幕，承载着数形结合思想和代数方法研究几何问题的基调，为接下来双曲线和抛物线的学习提供了基本模式和理论基础。

體会椭圆的定义的生成以及标准方程的推导过程，鼓励学生勇于探究、批判质疑，培养信息意识、乐善好学的精神素养和学习习惯;在应用解题的过程中，使得学生的理性思维得以提升，出现问题勤于反思，整体注重学生思维灵活性的培养。

重点是椭圆的定义及其标准方程，椭圆定义的应用以及标准方程的求解。其中，对定义中“”的理解，推导标准方程时，对代数式的化简，是本节课的难点。

学情分析：

在学习本节课前，学生已经学习了直线与圆的方程，对曲线和方程的思想方法有了一些了解和运用的经验，对坐标法研究几何问题也有了初步的认识。因此，学生已经具备探究有关点的轨迹问题的知识基础和学习能力，但由于学生学习解析几何时间还不长、学习程度也较浅，并且还受到高二这一年龄段学习心理和认知结构的影响，在学习过程中难免会有些困难.因此根据所学以及问题的引导进行自主探究和合作。

学习目标：

1、理解椭圆的定义：会用定义中的（定值）解决问题;如：①已知求;②判断满足某些条件的动点轨迹。掌握椭圆的标准方程：①能根据已知条件求解标准方程;②根据方程写出焦点坐标。

2、学生通过动手画椭圆、分组讨论探究椭圆定义、推导椭圆标准方程等过程，提高动手能力、合作学习能力和运用知识解决实际问题的能力，并渗透方程、分类讨论、类比的思想方法。

3、在形成知识、提高能力的过程中，激发学生学习数学的兴趣，提高学生的审美情趣，培养学生勇于探索、敢于创新的精神.

思路设计：

一、复习旧知，形成概念

演示卫星运行轨迹，直观感知椭圆形象。由圆带入，回顾圆的定义和标准方程以及画圆的方法，引出本节课内容，探究椭圆的定义和标准方程。让学生自主学习，按照教材中的实验叙述，进行实际操作，通过具体实践探讨其结果，并尝试归纳出椭圆的定义。

二、深入研究，揭示本质

根据定义以及点的轨迹方程求解步骤，小组合作探究完成。其中建系方式和根式的化简，教师给予及时引导，突破难点，辅助完成椭圆标准方程的推导。

三、学以致用，迁移深化

对于椭圆定义的应用以及标准方程的求解，采用讲练结合，从例题出发板书示范，逐步渗透对椭圆定义及标准方程的理解和运用。完成当堂达标，做到小组内自查，教师重点讲解，最后让学生总结本节课的内容，使学生自身对本节课有一个系统化的认识。

教学流程：

一、复习旧知，形成概念

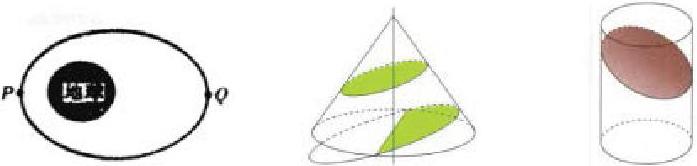
（一）课件投影：请同学们观察某卫星运行轨道图片，并说出其形状，然后提出问题引出本节内容。补充圆锥的斜截面是可能是椭圆。

1.你能描述一下椭圆吗？

2.椭圆的定义是什么？椭圆的方程又是怎样的？

然后，请同学们说一下，圆的定义？圆的标准方程？你有什么方法画出一个圆？

（设计意图：通过实例演示，让学生对椭圆的特征有初步认识，结合圆的定义，再进行椭圆定义的探究应是水到渠成。）

（简要实录：学生能说出部分行星运行轨迹是椭圆;老师提到圆锥的斜截面是椭圆，学生能想到，斜着去截圆柱面，也能得到椭圆;学生提出多种画圆的方法，学生的思维不断在发散，并且学生已经动起来，为接下来作椭圆生成实验做好准备。）

（二）课件投影：请同学们各自完成实验，并观察并思考（小组合作）：

1、动点的轨迹是什么形象？

2、动点运动过程中的不变量？

3、细绳的长度有要求吗？

请同学们试着描述椭圆的定义？

椭圆定义：平面内与两定点F1、F2的距离之和等于定长（大于∣F1F2∣）的点的轨迹叫做椭圆。

思考：细绳长度2a等于∣F1F2∣、小于∣F1F2∣时动点的轨迹？（突破难点1）

教师板书：一、椭圆的定义：平面内与两个定点，的距离之和等于定长（大于）的点的轨迹叫做椭圆。定点，叫做椭圆的焦点，两焦点的距离叫做椭圆的焦距。

（设计意图：使学生体会椭圆的定义从操作→观察→猜想→探究→形成概念的思维过程，培养学生科学合理分析问题的方法和习惯。）

（简要实录：学生用两个图钉和细绳，动手画出椭圆。学生通过讨论，能够说出动点运动过程中细绳的长度不变，细绳要比两个图钉之间的距离要长。结合预习情况，学生说出椭圆的定义，教师对“在平面内”“定长大于∣F1F2∣”进行强调，同时突破难点1。在此过程中，学生主动性明显提高，通过自己动手操作，更愿意分享自己的成果。）

二、深入研究，揭示本质

课件投影：请同学们回顾：动点的轨迹方程求解过程？

建系引导：看到你画出的椭圆，你将其放在直角坐标系中的什么位置方便、简洁？请同学们考虑椭圆自身的对称性。

设点、列式引导：对于带根号的表达式，我们总能想到平方去根号，有一个根式时，将其单独放在方程一边，像这样式子中有两个根式应该怎么操作呢？（将根式分别放置在等式的两侧，再平方。）（突破难点2）

三、学以致用，迁移深化

（一）课件投影：请学生完成下面的题目（学案例1），请学生说出解题过程，全体评价。

（二）课件投影：请学生完成下列题目（学案当堂达标）：

山东省临邑第一中学 孙晓丽