海流作用下自主航行船舶操控研究及应用
秦尧,房新楠,姚望,樊翔,邹康
(上海船舶研究设计院,上海 201203)
0 前言
当前全球约90%的贸易通过船舶运输, 海运业的碳排放量占全球总量的3%并呈快速增长趋势[1]。因此,船舶技术的革新将直接影响全球经济的发展与生态环境的改善。 面对降本增效、节能减排和安全航行等需求,智能化、无人化已成为船舶工程发展的重要方向。
在船舶正常航行时,需要对船舶的纵荡(即前进)、横荡(即横移)与艏摇(即转艏)三个自由度(3DOF)进行操控。 然而,大部分船舶仅安装了螺旋桨与舵两个操纵器。 有些船舶虽然装有侧推,在正常航行下侧推也是失效的。 因此,一般船舶往往都是欠驱动系统。 由于欠驱动船舶具有本质非线性和模型非完整的特性,自主航行船舶航行时的精确操控对传统的控制策略带来了挑战[2]。
自主航行船舶的航行操控主要依靠轨迹追踪技术实现。 近年来,随着无人船技术的快速发展,有关轨迹追踪问题的研究已取得了不少成果。 Godhavn[3]直接将船舶位置作为控制对象,基于反馈线性化和反步法设计了一种全局指数稳定的控制器,使得船舶在外界干扰下也能取得良好的追踪效果。Toussain 等[4]在反步法的基础上,通过输出反馈与航向角偏差的修正,实现了对直线以及曲线目标轨迹的追踪。 HEBERTT S R[5]针对气垫船提出了一种微分单调性与高阶滑模控制相结合的二阶轨迹控制器, 在获得平滑控制效果的同时又具有更强的鲁棒性。 程金[6]将外部环境力视为缓变干扰,基于反步控制法提出了一种全场景自适应控制器,通过理论推导证明了该控制器的全局稳定性,实现了船舶位置的动态追踪控制。 柳晨光等[7]建立了船舶运动的非线性状态空间模型,在对模型进行近似线性化的基础上设计了一种轨迹跟踪的线性模型预测控制器,该控制器充分考虑了控制输入输出以及控制增量的上下限,其仿真测试结果显示控制器具有良好的控制效果。王耀禄[8]利用滑模控制方法设计控制器,采用指数趋近律得出船舶的控制力,该控制器能够同时实现船舶对封闭轨迹和开放轨迹的跟踪。
上述研究在船舶控制律设计方面取得了较大的进展,这些成果都是基于静水环境的,并没有考虑海流的作用。 然而船舶在实际航行过程中时刻会受到海流的影响,因此有必要设计一种适应海洋影响的控制器。 本文针对一般船舶航行特征建立三自由度船舶运动模型,同时根据Lyapunov 稳定性方法以及级联系统理论设计一种考虑海流影响的轨迹追踪控制器。 通过预定航线、航向与实际航线、航向的对比验证控制器的可靠性。 在此基础上,本文根据螺旋桨推力模型[9]与 舵机舵力模型[10]求解不同 海流情况下的船舶轨迹追踪时的螺旋桨转速与舵角。通过分析结果可知,海流对螺旋桨转速的影响比对舵角的影响更为明显。 海流不但影响螺旋桨的转速变化幅值而且也影响转速的变化周期。 海流强度越大、周期越长,螺旋桨转速的变化幅值也就越大;此外,随着海流的周期性变化,螺旋桨转速也会出现相同周期的响应。
1 船舶运动数学模型
当前,船舶轨迹追踪问题一般采用Fossen[11]模型。 在海流作用下,船舶运动的三自由度数学模型可以表示为
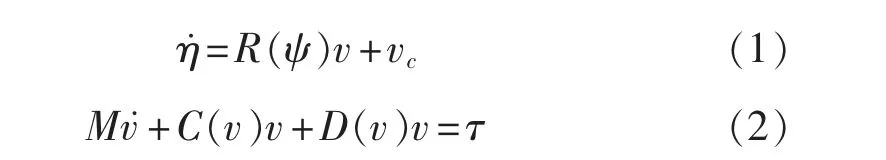
式中:η=[x,y,φ]T为大地坐标系NED 中船舶的平面位置与航向角,v=[u,v,r]T为船舶随体坐标系中的纵向速度、横向速度与转艏角速度,两者之间的坐标转换矩阵可以表示为
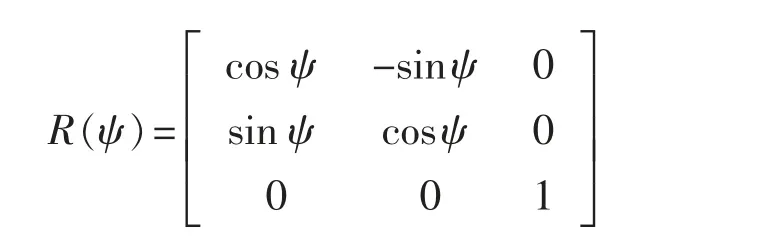
vc=[vcx,vcy]T为海流的流速矢量,惯量矩阵为

柯氏力与向心力矩阵为
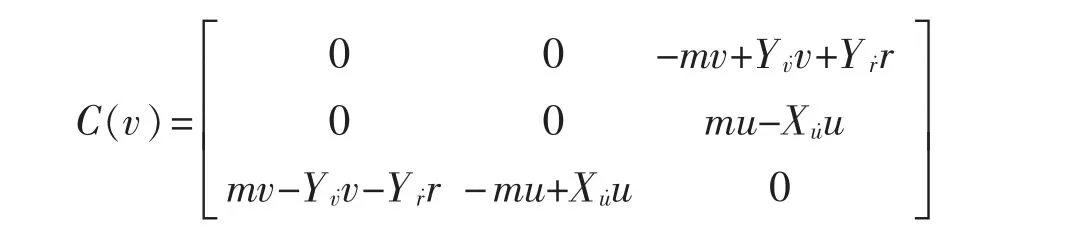
阻尼矩阵为
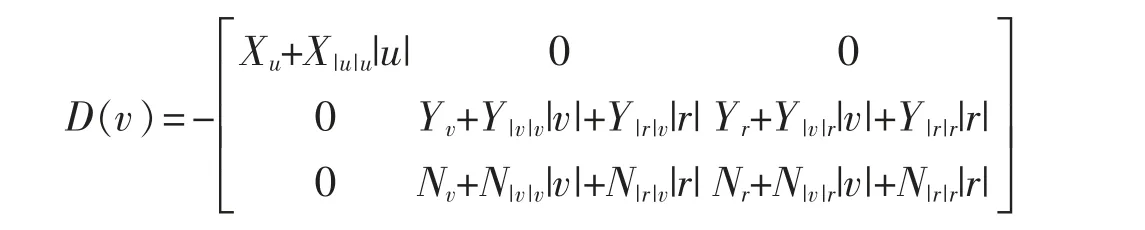
式中:m为船舶质量;Iz为船舶艏摇惯性矩;Xu˙、Yv˙、Y˙r、Nr˙、Xu、X|u|u、Yv、Y|v|v、Y|r|v、Yr、Y|v|r、Y|r|r、Nv、N|v|v、N|r|v、Nr、N|v|r、N|r|r均为水动力学系数。 τ[τ1,τ2,τ3]T为船舶纵向、横向上的控制力与转艏方向上的控制力矩。
2 轨迹追踪控制器设计
定义追踪目标的状态为ηd=[xd,yd,φd]T,根据级联系统理论,子系统状态变量可以定义为
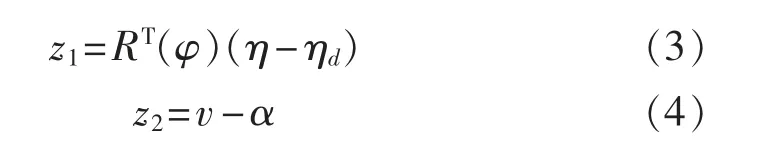
式中:α 为轨迹追踪的期望速度,为待求解量。
根据Lyapunov 理论建立第一个子系统z1的Lyapunov函数:
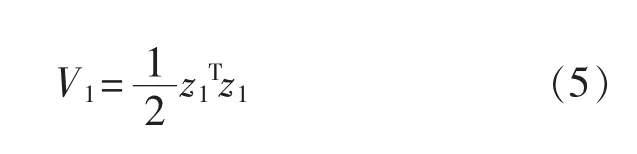
则V1对时间求导得:
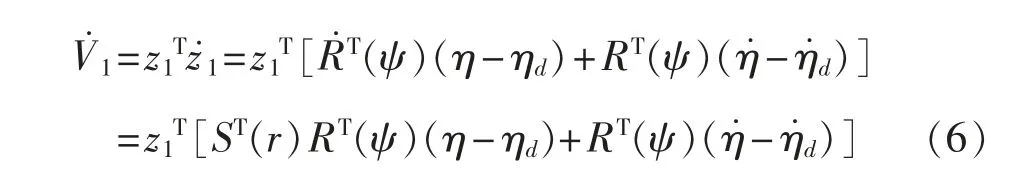
将式(1)与式(3)代入式(6),可得:
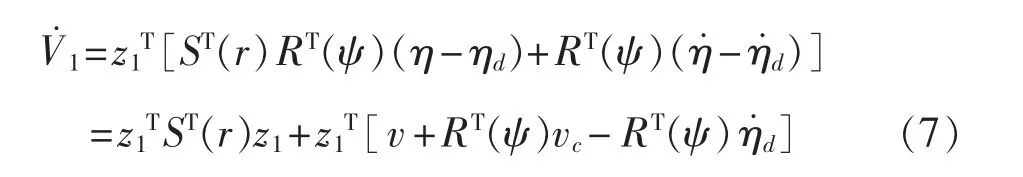
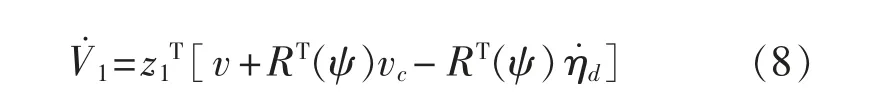
再将式(4)代入(8)可得:
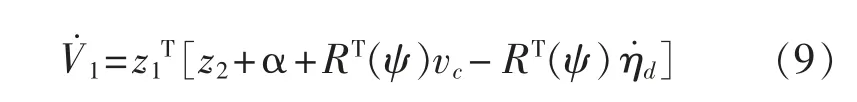
于是,期望速度α 可以设为
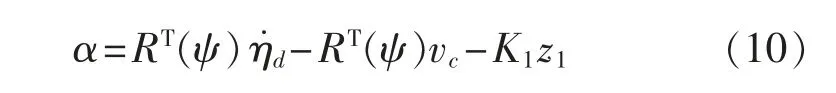
式中:K1对角常数矩阵,且K1>0。
将式(10)代入式(9)后可得:

从上式可知,当z2→0 时V1在0 附近全局一致稳定。
此外,根据上述推导还有如下关系:
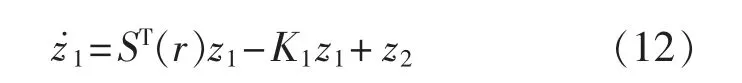
随后,对于子系统z2,有Lyapunov 函数为
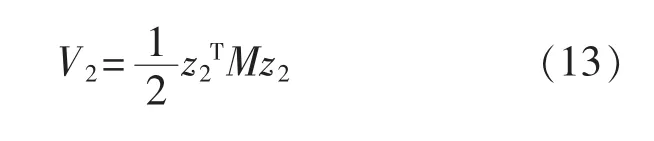
对V2求导得:
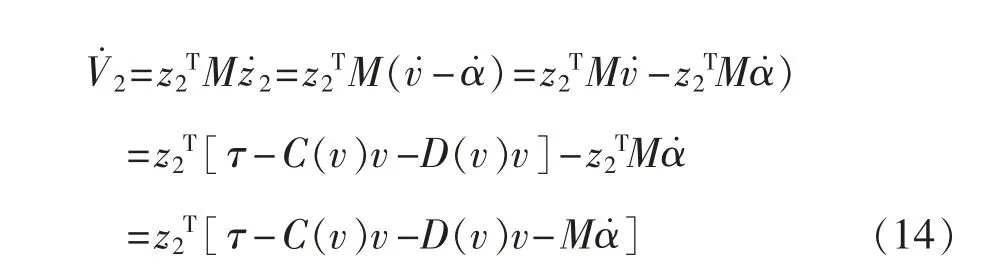
于是,控制荷载τ 可以设为

将式(15)代入式(14),则:
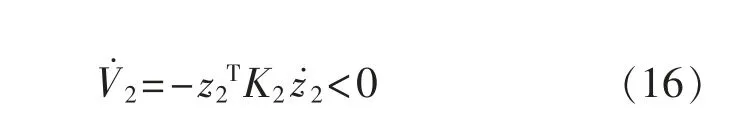
这表明V2在0 附近全局一致稳定,z2也在0 附近全局一致稳定。 结合子系统z1的稳定性分析可知,整个系统在(0,0)附近全局稳定。
3 船舶操纵数学模型
船舶的操纵装置通常为螺旋桨与舵。 自主航行船舶利用控制器计算得到的操纵荷载需要进一步转换为螺旋桨转速与舵角的指令。
螺旋桨的推力T与扭矩Q[9]可以表示为
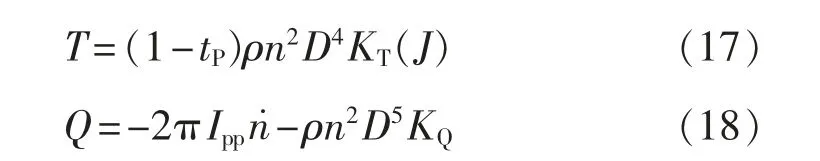
式中:J=u(1-wP)/(nD)为桨的进速系数,tP为桨的推力减额系数,wP为桨的伴流系数;ρ 为水的密度;n为桨转速;D为桨直径;KT为推力系数;Ipp为桨的转动惯量;KQ为扭矩系数。
舵上产生的力(XR,YR)与力矩(NR)[9]可以表示为
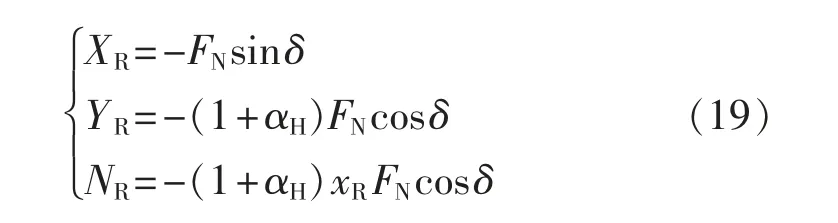
其中:
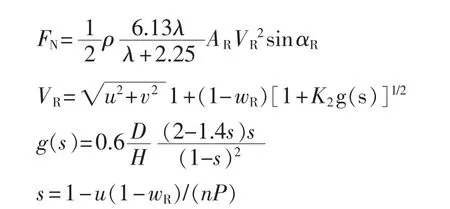
式中:λ 为舵的展弦比;AR为舵面积;αR为舵的入流角;wR为舵的伴流系数;K2为与螺旋桨旋转方向有关的常数,这里取0.935;H为舵的高度;P为桨的螺距。
当控制器计算得到操控所需的控制荷载τ=[τ1,τ2,τ3]T时,令T=τ1,NR=τ3便能求得对应的螺旋桨转速n与舵角δ。
4 仿真与分析
基于Python 语言对上述数学模型进行编程,并以某大型商用船舶为对象进行数值仿真,船、桨、舵的主要参数如表1 所示。 船舶在规划航行任务时,会按照航海习惯设置航路点,将整个航线划分成若干航段, 每个航段上以固定平均航速沿恒向线[12]航行。 该船的航线共划分为7 段,各不同航路点(含起始点)的坐标向量分别为纬度=[0°N,3°N,4°N,9°N,12°N,12°N,10°N,8°N], 经度=[150°W,147°W,144°W,141°W,135°W,122°W,115°W,113°W],各航段 上的 航速分别为(15,14,13,15,13,15,14)kn(节)。 船舶在海上航行,必然会受到海流的影响,将海流的速度表示为[Vcsin(t/T),Vccos(t/T)],其中,t为时间,T 为海流变化的周期。
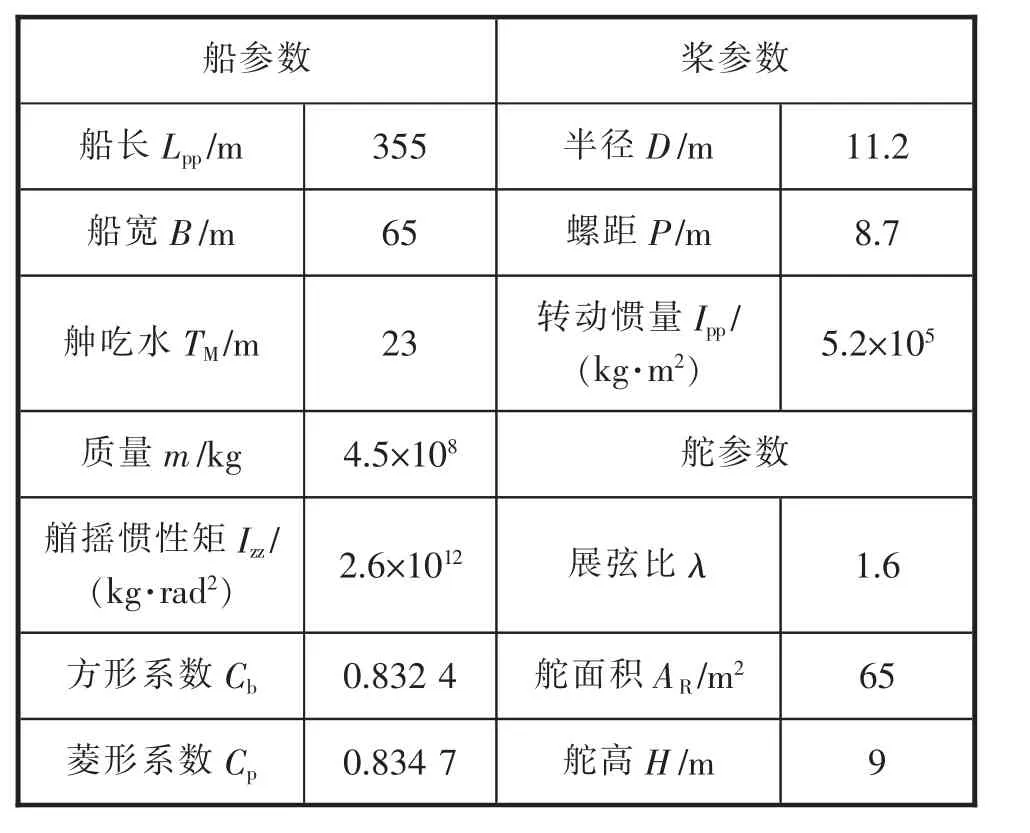
表1 某大型船舶船、桨、舵主要参数
图1 展示了不同海流条件下自主航行船舶的实际航线、航向与预定航线、航向的对比。 通过对比可以发现,各实际值与预定值均吻合良好。 这表明所建的模型能实现自主航行船舶的准确操控且具有较好的鲁棒性。图中的N、E 表示船舶分别在正北和正东方向航行的距离。
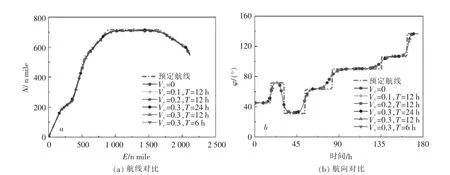
图1 实际航线、航向与预定航线、航向对比
图2 展示了螺旋桨转速在不同海流条件下的响应。 分析结果可知,在海流影响下,螺旋桨转速组成可以分为两部分:一部分是在静水下完成预定航行任务所需的转速;另一部分是为抵消海流对船速的影响而额外增加的转速响应。 海流不但影响螺旋桨的转速变化幅值, 而且也影响转速的变化周期。海流强度越大、周期越长螺旋桨转速的变化幅值也就越大。 由于海流的周期性变化,螺旋桨转速的时间变化序列中也会出现相同周期的响应。

图2 螺旋桨转速在不同海流条件下的响应
图3 展示了舵角在不同海流条件下的响应,结果显示, 在不同海流条件下舵角响应总体上没有发生变化。 这说明海流对舵角的影响明显小于对螺旋桨转速的影响。 通过局部放大观察发现,海流的流速越大、周期越长,舵角的响应幅值也会有小幅增大。

图3 舵角在不同海流条件下的响应
5 结语
针对自主航行船舶实际营运需求,建立三自由度运动模型,将Lyapunov 稳定性方法与级联系统理论相结合,设计了一种计及海流影响的轨迹追踪控制器,并基于Python 语言完成了程序编码。 设置预定的航线与航向,并运用程序计算了多种海流干扰下实际的航线与航向,结果显示在海流影响下的航线、航向与预设值高度吻合,表明设计的控制器具有良好的准确性与鲁棒性。 在此基础上,根据螺旋桨的推力模型与舵的舵力模型求解不同海流情况下船舶轨迹追踪时的螺旋桨转速与舵角响应,结果表明, 海流对螺旋桨转速的影响比对舵角的影响更为明显, 不但影响螺旋桨的转速变化幅值而且也影响转速的变化周期。 海流强度越大、周期越长,螺旋桨转速的变化幅值也就越大。 此外,随着海流的周期性变化, 螺旋桨转速也会出现相同周期的响应。

