考虑避障的船舶轨迹跟踪滑模控制策略
施文煜,姚怡芝,姚望
(上海船舶研究设计院,上海 201203)
0 前言
随着海上贸易需求的增加,海洋运输蓬勃发展,海运作为对外贸易增长及发展的推动者,对我国建设海洋强国有着极其重要的作用,在国家发展建设及人民日常生活中都有着极其重要的影响。 大型散货船作为代表性船型,在国际航运市场占比逐年递增。 在众多类型的船舶中,按照控制输入向量空间维数是否与船舶广义坐标向量空间维数相等,即船舶的独立控制输入量是否等于被控制自由度的数量,可分为全驱动船舶和欠驱动船舶,大多数船舶为考虑经济性设计为欠驱动形式,同时,在复杂海况下执行机构发生损坏时,全驱动船舶也将成为欠驱动系统,产生相应的控制问题。 因此,开展欠驱动船舶控制研究有助于提高整个船舶系统的鲁棒性和稳定性,对船舶精确航行有着十分重要的现实工程意义。
从非线性、欠驱动、船舶模型参数易控制三个方面对船舶轨迹跟踪控制策略进行研究。 目前,常用的轨迹跟踪控制策略有PID 控制、 反步控制、模糊控制、神经网络控制和滑模控制等。 文献[1]对于前驱动无人船轨迹跟踪问题,采用反步控制思想对控制律进行设计,并对所设计控制律与PID 控制方法进行比较,表明基于反步法设计的控制器具有更好的跟踪性能。 文献[2]设计了一种带干扰观测器的反步控制器对存在未知外界干扰的轨迹跟踪问题进行研究,在解决传统反步策略微分爆炸问题的同时增强了系统的抗干扰能力,加快了误差收敛速度。 文献[3]等提出一种模糊自适应轨迹跟踪控制策略,采用模糊系统来实现模型未知干扰的自适应逼近,并采用Lyapunov 稳定性理论证明了闭环系统的稳定性,仿真结果表明该控制方法起到了较好的抗干扰作用。 Sonnenburg 等[4]分别设计比例积分级联控制器和非线性反步控制器使船舶收敛于一条参考轨迹,并通过仿真测试表明在跟踪速度及艏向角变化较大时的轨迹, 采用反步控制能更有效地对轨迹进行跟踪。Aguiar 等[5]针对船舶存在较大建模参数不确定的情况设计了一种能够在二维及三维空间中自适应切换的非线性轨迹跟踪控制器,将自适应控制与基于Lyapunov 非线性控制相结合设计控制律,使位置误差收敛至零附近,从而渐近跟踪上任意一条经过时间参数化的光滑有界曲线。 Ismial 等[6]针对传统滑模控制会产生抖振问题, 提出了一种新的鲁棒动态区域自适应滑模控制方法,可以有效减小外部干扰和抖振的影响。 此外, 仿真结果表明该控制策略优于自适应滑模控制策略及模糊控制策略。
综合考虑上述方法,从控制器稳定性及实用性等角度出发, 同时考虑船舶航行中的避障需求,引入人工势场法实现船舶自主避障。基于Lyapunov 稳定性理论镇定纵向速度与艏向角误差,以分析闭环系统的稳定性。 最后通过仿真计算验证了所设计控制策略的有效性。
1 船舶运动模型
考虑欠驱动船舶的运动特性,根据文献[7]建立如下运动模型:
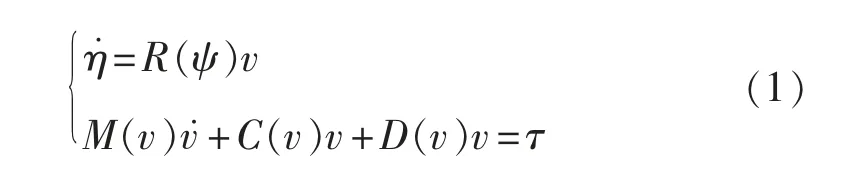
式中:η=[x,y,ψ]T为位姿向量,主要包括纵向位置,横向位置及艏向角;v=[u,v,r]T为纵向速度、横向速度及艏向角速度构成的速度向量;坐标转换矩阵R(ψ)、惯性矩阵M(v)、水动力阻尼矩阵D(v)、科式向心力矩阵C(v)分别为
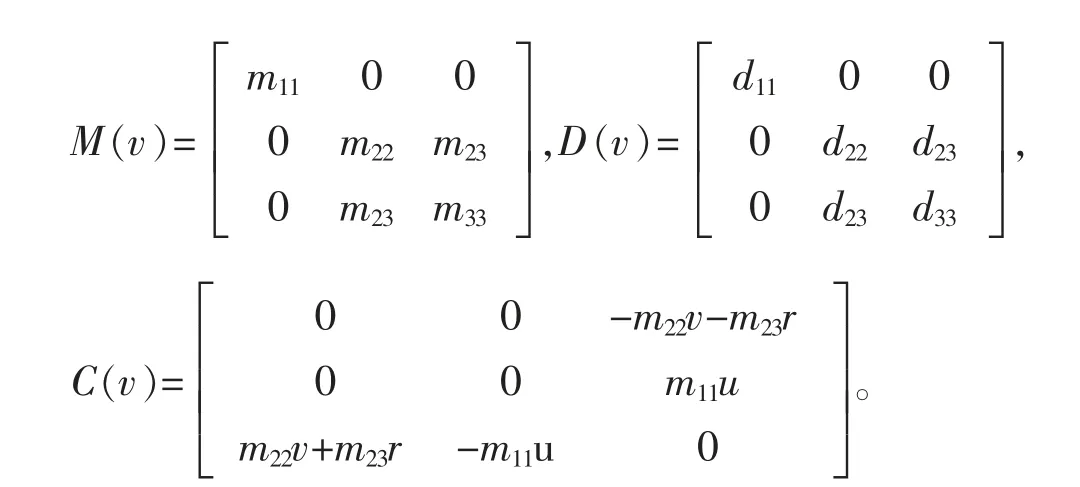
以某散货船为研究对象展开研究,主要模型参数如表1 所示。

表1 某散货船模型参数
欠驱动船舶以螺旋桨及方向舵为执行机构,为实现纵向、横向及艏向三个自由度方向上的控制,可将式(1)简化为

轨迹跟踪示意图如图1 所示,选取期望轨迹为ηr=[xr(t),yr(t)]T,假设该期望轨迹光滑有界,船舶在运动中控制输入有界,且船舶沿着期望轨迹作无差运动,则船体坐标系原点与当前轨迹P 重合,因此船舶运动速度与P 点速度相等[8],其大地坐标系下位置坐标P 为P=[xr(t),yr(t)]T,当前轨迹点P 的速度大小为,侧滑角β=atan2(v˙,u˙),选择参考偏航角ψr=atan2(y˙r,x˙r),其中atan2(x,y)为能够确定角度所在象限的反正切函数。

图1 水平面轨迹跟踪示意图
考虑参考轨迹上任意一点与船舶当前位置,定义惯性坐标系下的轨迹跟踪位置及角度误差为
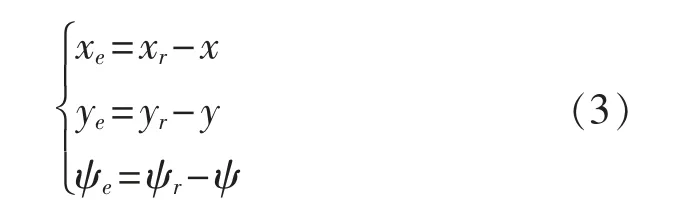
为便于控制器设计,根据几何变换,定义体坐标系下的位姿误差为
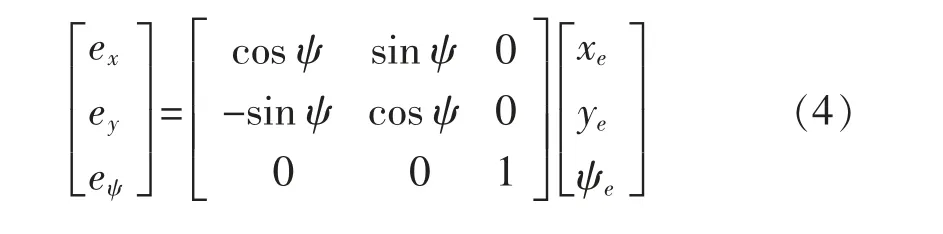
2 控制策略
2.1 控制目标
对于水平面轨迹跟踪问题,设计鲁棒性强的控制律使轨迹跟踪误差收敛于零附近任意小的邻域内,如公式(5)所示,以保证船舶能跟踪上期望的轨迹点并沿参考轨迹运动。
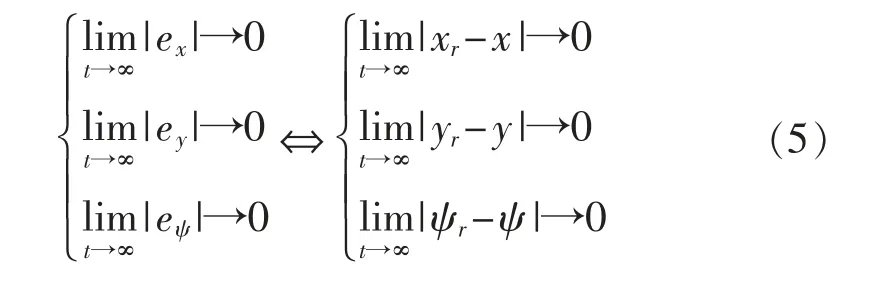
建立如图2 所示轨迹跟踪控制框架,基于自适应动态面方法设计轨迹跟踪控制器,使被控船舶位姿信息与虚拟位姿状态量趋于一致。
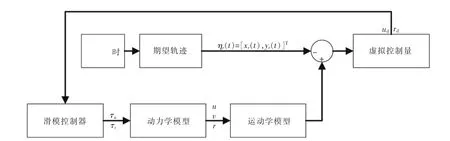
图2 轨迹跟踪控制框架
2.2 运动学控制器设计
对于船舶轨迹跟踪问题,一般通过引入系统的运动状态误差空间,将轨迹跟踪控制问题转化为误差镇定问题。 对式(4)进行简化可得船舶误差模型为
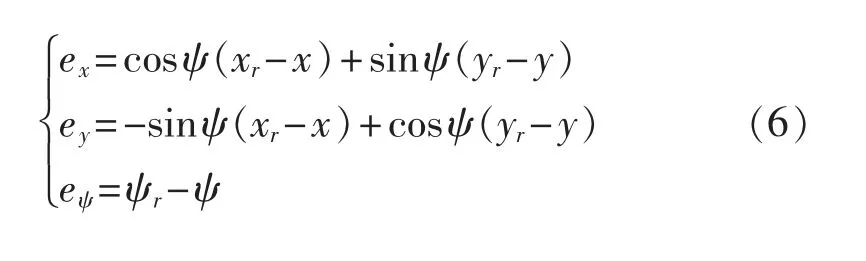
对上式求导可得:
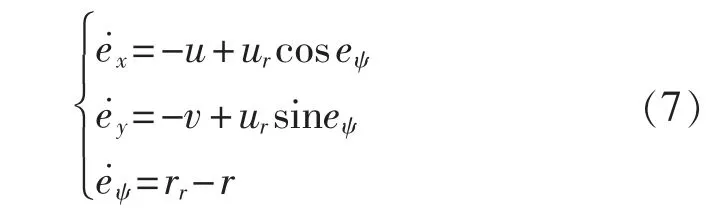
由于船舶横向速度较小, 假设其可以忽略,即定义船舶横向参考速度vr=0,因此船舶纵向参考速度。
首先定义第一个Lyapunov 函数为

式中:k1>0。
对式(8)求导可得:

以纵向速度u 及艏向角速度r 为虚拟控制输入,则可选择期望纵向速度ud及艏向角速度rd为:
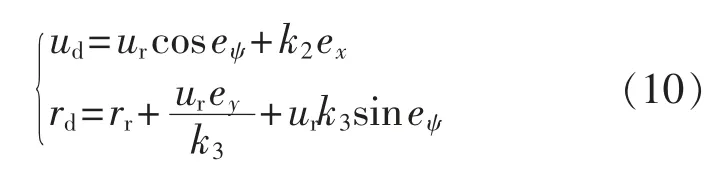
2.3 避障设计
针对船舶航行环境中存在的障碍物情况,采用人工势场法使船舶在运动过程中有效避障。 为方便避障控制器的设计, 假设船舶的航行安全半径r 及通信半径Ri,满足Ri≫ri。
基于控制目标(5),使船舶在跟踪参数轨迹的同时避免障碍物碰撞问题,即
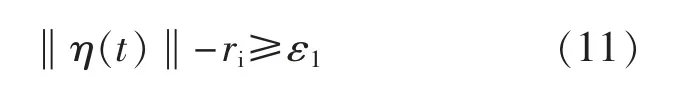
采用人工势场法对船舶参考路径进行调整,生成无碰撞的参考路径以实现障碍物避让。 采用如下人工势函数:

式中:Ri为障碍物外围可探测区域半径 (即船舶进入该区域范围内即可探测到障碍物的存在);ri为障碍物半径;为船舶船到障碍物的距离;(xpi,ypi)为障碍物的位置。
对船舶收受到的斥力Γi在纵向及横向上求导可得:

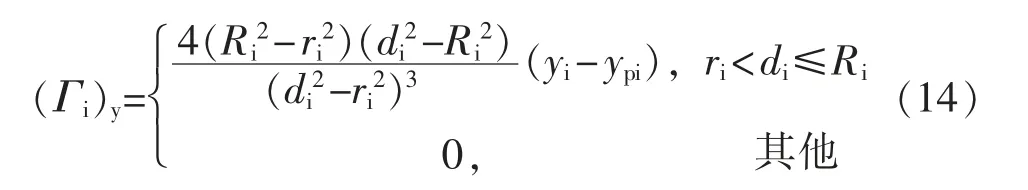
定义虚拟力向量为
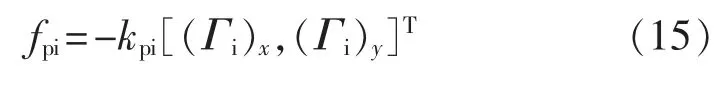
式中:kpi>0。
定义体坐标系下的避障调整量为
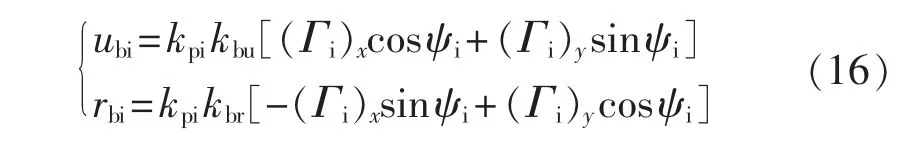
式中:kbu>0,kbr>0。
调整期望速度及期望角速度,得到船舶的期望速度为
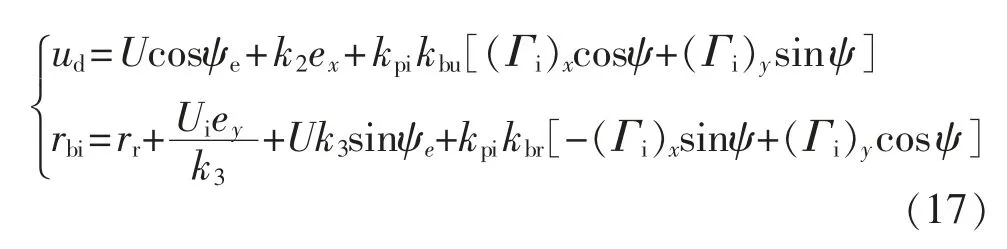
2.4 动力学控制器设计
2.4.1 镇定纵向速度误差
由式(2)可知纵向速度模型为
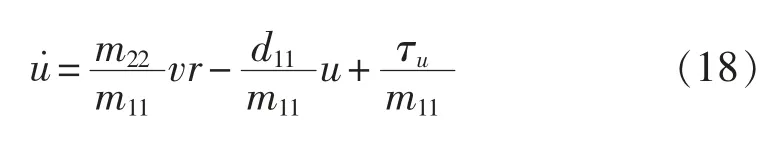
定义纵向速度误差为

设计积分滑模面

式中:k1>0。
对式(20)求导得
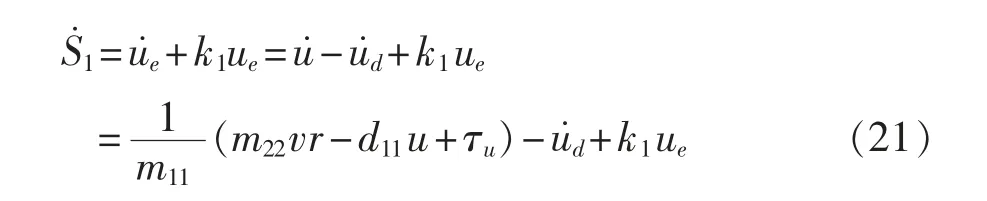
为使S˙1=0,选取等效控制律为
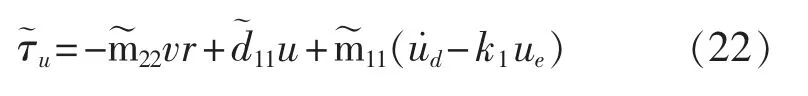
在滑模控制中,为了消除抖振,采用如下饱和函数代替符号函数

式中:d1>0。
那么,则纵向速度控制律为
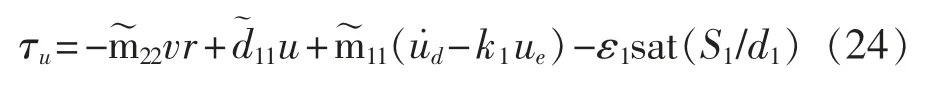
定义Lyapunov 函数为

对式(25)两边同时求导可得

根据式(23)饱和函数特性可取ε1为

式中:λ1>0。
那么,式(26)有V˙1≤-λ1|S1|。 由此可知,在滑模控制律的作用下,满足从任意位置状态点的滑模到达条件, 即稳定于S1=0 处, 速度误差ue也稳定于零,纵向速度误差镇定。
2.4.2 镇定艏向角误差
根据式(2)可知,艏向角运动模型为

定义横向速度误差为

求导可得
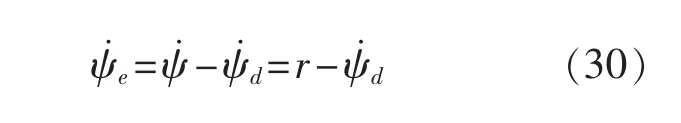
设计如下滑模面

式中:k2>0。 定义虚拟控制量,对上式两边求导可得

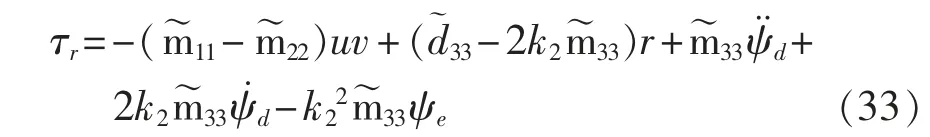
选取如式(23)所示趋近律,则艏向角控制律为
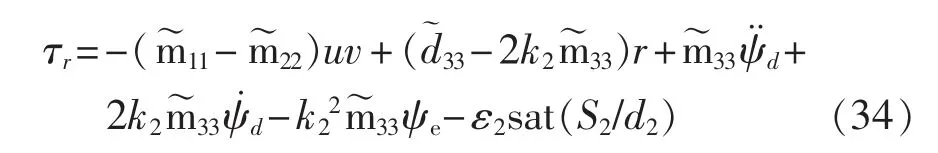
选取Lyapunov 函数

对上式求导可得
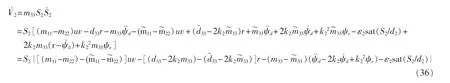
根据式(23)饱和函数特性可取ε2为
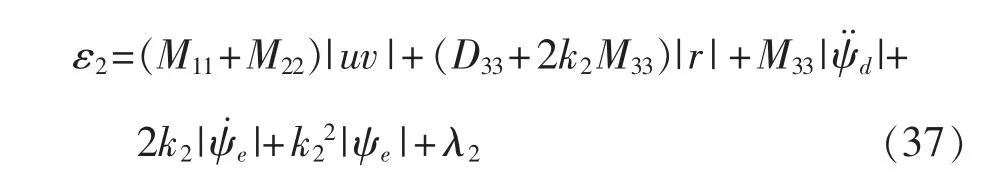
式中:λ2>0。
那么,式(36)有V˙2≤-λ2|S2|。 由此可知,在滑模控制律的作用下,满足从任意位置状态点的滑模到达条件,即稳定于S2=0 处,艏向角误差ψe也稳定于零,艏向角误差镇定。
3 轨迹跟踪仿真结果
为验证轨迹跟踪控制器设计的有效性,以某散货船为对象进行仿真计算。
3.1 直线轨迹跟踪仿真

图3 直线轨迹跟踪避障仿真曲线
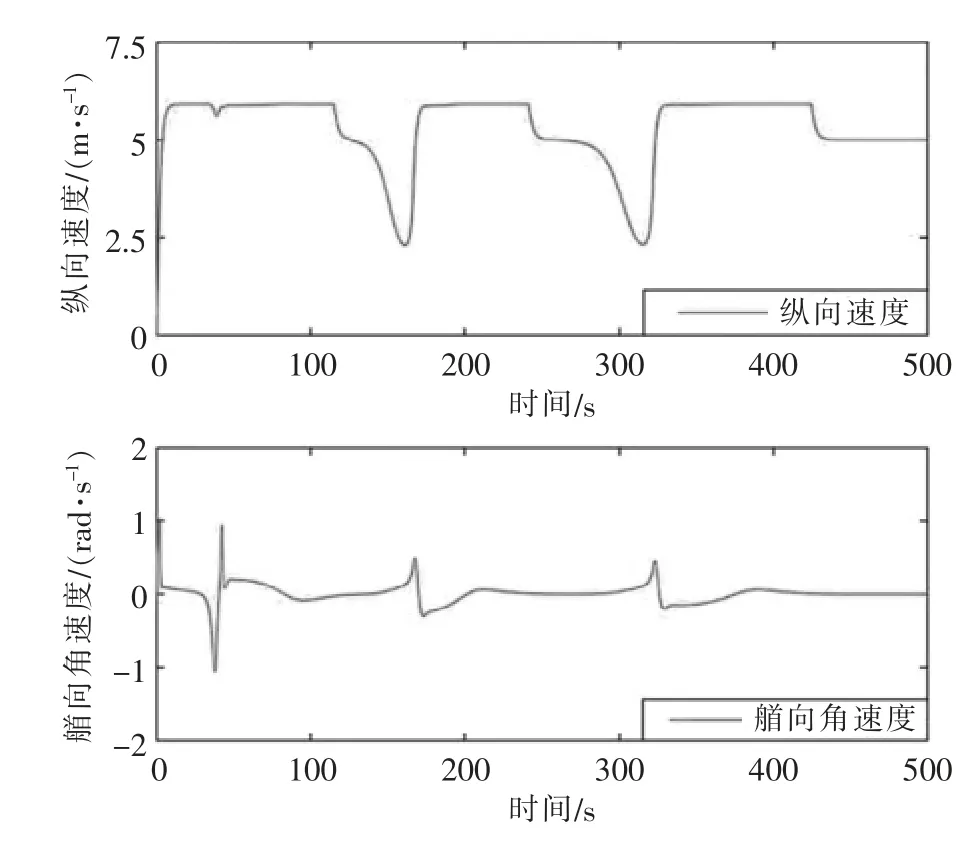
图4 纵向速度及艏向角速度响应曲线

图5 纵向误差及横向误差响应曲线
3.2 正弦轨迹跟踪仿真
设定船舶轨迹跟踪期望轨迹为xr=4.8t,yr=480 sin(0.01t),仿真结果如图6~图8 所示。 图6 给出了考虑避障的正弦轨迹跟踪仿真效果图,结果显示在不同曲率下,船舶能快速跟踪上期望轨迹并有效避让障碍物。 图7 展示了某船纵向速度及艏向角速度曲线, 可以看出速度在障碍物处发生突变,并在短时间内进行调整。 图8 给出了误差响应曲线,误差在避障后能较快趋于零附近,表示该控制策略有较好的跟踪性能。
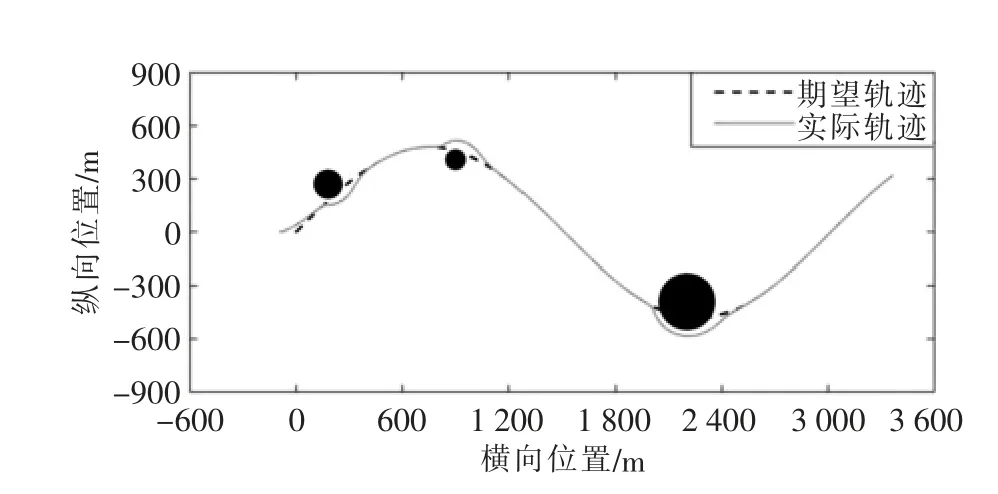
图6 正弦轨迹跟踪避障仿真曲线
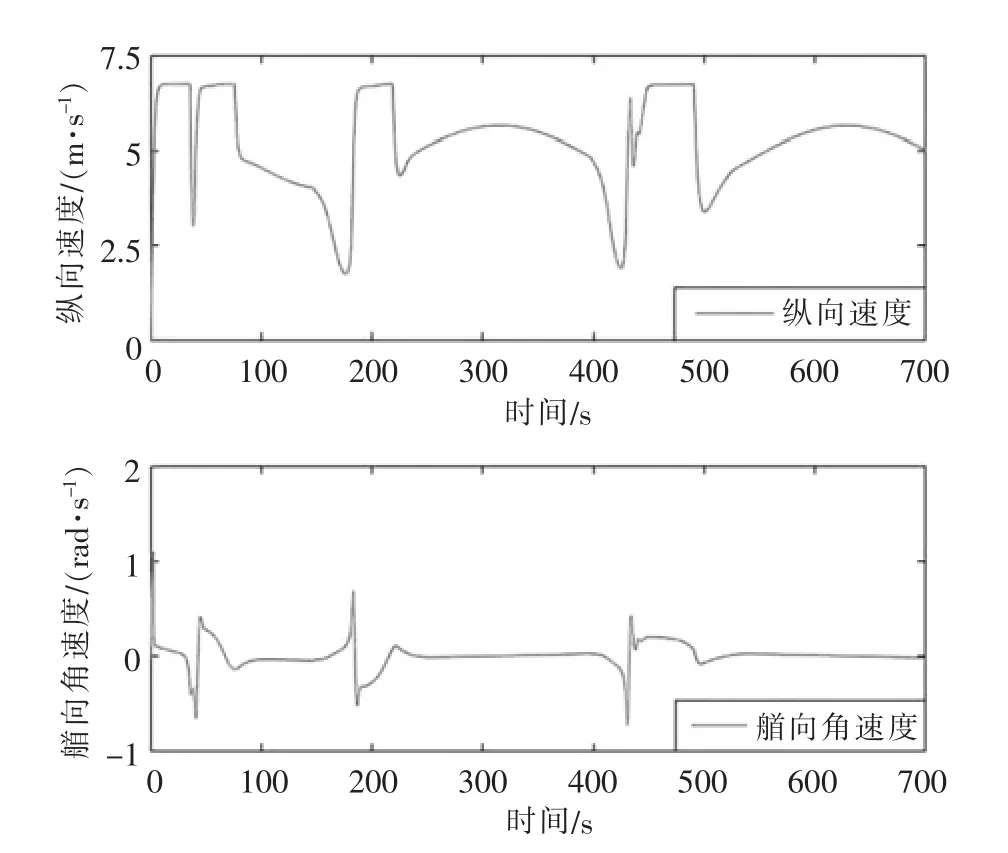
图7 纵向速度及艏向角速度响应曲线
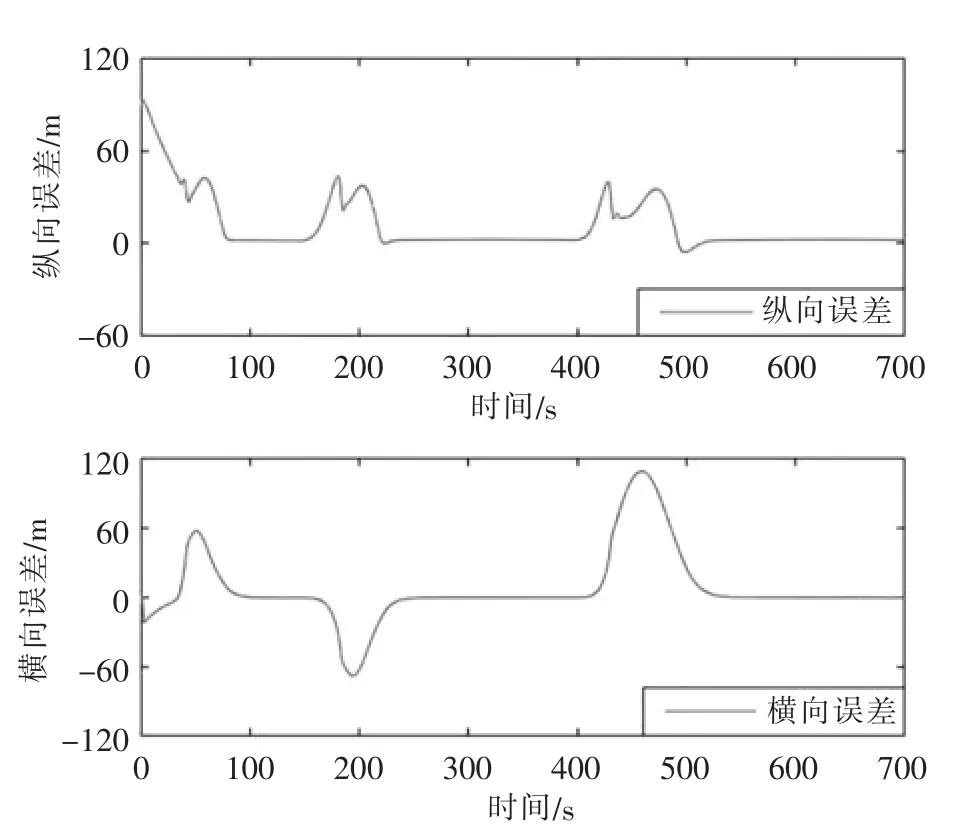
图8 纵向误差及横向误差响应曲线
4 结语
针对某散货船轨迹跟踪问题,建立船舶运动模型,采用积分滑模非线性控制理论来克服传统滑模引起的抖振问题, 进行船舶轨迹跟踪控制器设计,并结合势函数对跟踪轨迹进行调整,从而能有效避让障碍物。 仿真试验结果表明,所设计控制器有较好的控制性能及较强的自适应性和鲁棒性。

