海上风电四桩导管架基础承载特性数值模拟研究

孙焕锋，葛 畅，许海波，陈凤云

(1.中国电建集团华东勘测设计研究院有限公司，浙江 杭州 311122；2.浙江华东工程咨询有限公司，浙江 杭州 311122；3.浙江大学海洋学院，浙江 舟山 316021)

0 引 言

近年来，我国海上风电事业发展十分迅猛，到2019年底，全国海上风电累计装机593万kW，风电装机占全部发电装机的10.4%[1]。随着海上风电大力发展，海上风电基础形式也越来越丰富。目前，国内外较为常见的海上风电基础形式有单桩基础、重力式基础、高承台群桩基础、三脚架基础、吸力桶式基础、导管架基础等。其中，导管架基础是一种由上部导管架结构与四根角桩两部分构成的三维框架结构，因其刚度大、结构质量轻、适用水深范围广、对场地土体依赖性小等优点，近年来逐渐应用于海上风电领域中[2]。

海上风电基础主要受到上部风机荷载和风浪流等环境荷载作用，由于其为高耸结构，其荷载形式表现为弯矩和水平力较大，受到的竖向力相对较小[3]。目前国内外对单桩基础的承载特性已经进行了大量研究[4-7]，而关于导管架基础承载特性的研究相对较少[8-13]。数值模拟方面，袁志林等[8]采用ABAQUS建立了四桩导管架桩基水平承载特性的有限元模型，分析了水平土压力系数对承载性能的影响。李光銮等[9]通过ABAQUS建立了饱和粘土中的桩土模型，研究了导管架基础的水平承载性能。Wen等[10]采用数值模拟的方法对沙土中的四桩导管架基础承载特性开展了研究。室内试验方面，朱斌等[11]采用离心机模型试验研究四桩导管架基础在饱和砂土中的承载性能。钟超等[12]建立导管架平台缩尺模型，通过现场试验加载不同幅值与次数的循环荷载，研究了桩基弱化对导管架平台水平承载性能的影响。祝周杰等[13]通过离心机模型试验，研究了导管架基础的p-y曲线并对其进行修正。

四桩导管架基础因其开展海上现场试验非常困难而且需要大量的人力物力，成本高昂。本文以江苏某海上风电项目为研究背景，采用ABAQUS数值模拟方法，开展四桩导管架基础承载特性分析研究，确定导管架基础的水平承载力，分析桩基受力变形特性，研究结果可为海上风电工程的导管架基础设计提供参考。

1 工程概况

江苏某海上风电场的海上升压站导管架基础采用上部导管架结构与四根角桩结合。上部导管架结构长宽均为24 m，导管分两种，一种直径为1.1 m，壁厚为0.032 m，共有16根，另一种直径为0.8 m，壁厚为0.024 m，共有8根。导管架基础角桩采用4根直径为3.0 m，桩长75 m，壁厚36 mm的钢管直桩，角桩埋深约为49.4 m。导管架结构示意如图1所示。

图1 导管架基础结构示意

2 导管架基础数值模型

2.1 数值模型参数设置

四桩导管架基础由上部导管架结构和4根角桩两部分构成。其中，上部导管架机构的主要作用是将海上升压站所承受的风、浪、波流等水平荷载传递给下部的4根角桩。采用ABAQUS建立四桩导管架基础数值模型，将上部导管架结构简化为空间桁架，如图2所示。

图2 导管架基础ABAQUS数值模型

角桩为钢管桩，Q235材质，上部导管架与下部桩基均选用线弹性本构关系。将上部导管架结构与下部桩基视为整体，不考虑下部桩基与上部结构的滑移及摩擦。因为角桩刚度与土体差别较大，计算中容易发生不收敛现象，所以采用等效抗弯刚度法，将钢管桩转化为实心桩，对其密度以及杨氏模量进行折减，折减后抗弯刚度不变，导管架与桩基参数见表1。土地基模型假设为长方体，土体模型长宽高分别为160、60、80 m，桩与边界距离远大于10D，因此可忽略边界效应的影响。土体本构模型选择Mohr-Coulomb模型，为弹塑性体，为便于计算收敛，在对水平承载性能影响不大的情况下对土层进行简化，土层数值模拟参数见表2。

表1 导管架基础模型的材料参数

表2 土体物理力学参数

2.2 桩-土接触面接触设置及边界约束条件

在ABAQUS中，设置桩周土体与桩基的接触模型时，采用通用接触，选择主-从表面接触算法，为了确保计算能够收敛，将刚度较大的桩基表面设为主面，土体接触面设为从面。接触面切向接触采用“罚”函数设置相应摩擦系数，摩擦系数设为0.36，为了防止主-从接触面对应的网格发生入侵现象，对法向接触采用硬接触，即桩基与土体仅在完全压密时才会传递法向应力，当桩基与土体间存在间隙时则不会传递法向应力。同时，允许桩-土接触面在接触后分离。数值模型底部施加3个方向上的位移约束，使土体底部固定，对4个侧面施加两个方向的位移约束，仅让土体在竖直方向发生变形，顶面则为自由面。

2.3 划分网格及平衡地应力

上部导管架结构采用两结点线性三维桁架单元(T3D2)。为了防止计算结果出现交替的梯形网格等严重的网格畸变，即出现“沙漏模式”导致结果失真，下部桩基和地基模型采用八结点六面体线性减缩积分单元(C3D8R)。桩周10D范围内对土体网格进行加密。平衡地应力的方法采用循环迭代导入odb文件法，在施加水平荷载之前，将重力赋加在数值模型，得到模型的初始地应力。

2.4 加载方式

常规试桩试验中水平静载试验一般采取水平维持荷载法，采用荷载加载方式，每隔一定时间测量水平位移[3]。数值模拟加载方式若采用水平力加载方式，结果只有该特定荷载下的水平位移，得到的是离散的水平荷载-位移(Q-s)点。因此，本数值模拟加载方式采取位移加载，能够得到连续的连续的水平荷载-位移(Q-s)曲线。

3 导管架基础承载力特性分析结果

3.1 水平荷载-水平位移特性曲线

通过对四桩导管架顶部两点进行水平位移加载进行模拟分析，得到了导管架顶部水平荷载-水平位移曲线(Q-s)曲线，如图3所示。从图3可以看出，A点之前，水平位移随着荷载的增加而线性增加；B点以后，水平位移随着荷载的增加缓慢增加；C点(水平位移为0.2 m)以后，水平承载力曲线基本保持不变，承载力基本不再增长，说明C点处对应的水平承载力即为该四桩导管架基础的极限水平承载力，为17 MN。

图3 承台水平荷载-位移(Q-s)

图4为四桩导管架基础的水平方向上的桩土位移，为了便于观察，将变形系数设为10倍。从图4可以看出，靠近加载点一侧的两根桩有明显的向上移动现象，远离加载点一侧的两根桩有明显的向下移动现象，分别为上拔桩与下压桩。

图4 水平方向上位移(放大10倍)

3.2 水平荷载-竖向位移特性曲线

由于导管架基础结构较高，受到水平荷载时容易出现较大的倾覆弯矩。上拔桩及下压桩顶部竖向位移随着水平荷载的变化趋势，如图5所示。当水平荷载较小时，上拔桩及下压桩的竖向位移与水平荷载呈线性变化；随着水平荷载逐渐增大，上拔桩开始出现上拔效应，当荷载逐渐接近导管架基础的极限承载力时，上拔桩竖向位移发生陡增现象，说明此时导管架基础已经发生失稳破坏。由于上拔桩的竖向位移对导管架基础的稳定性影响较大，在进行导管架基础设计时要注意上拔效应，从而避免上拔桩被拔出引起的基础破坏。

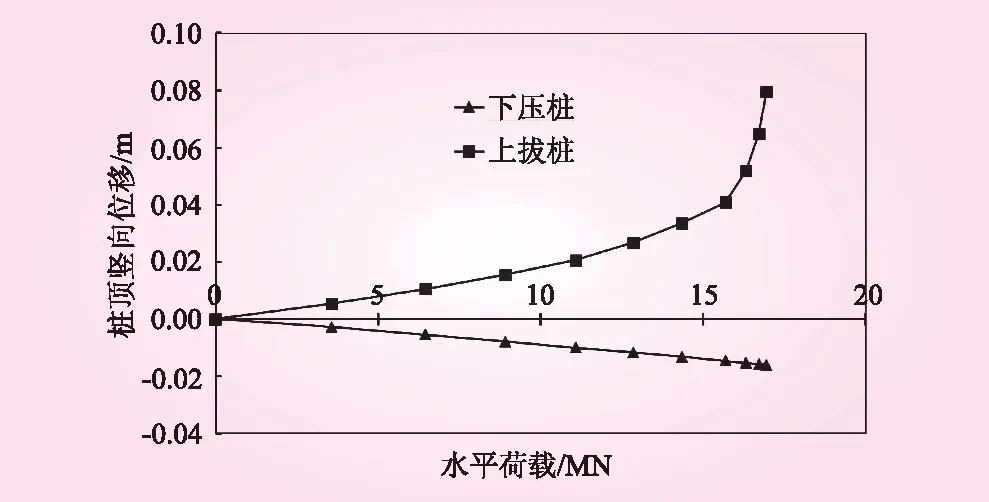
图5 水平荷载-竖向位移曲线

3.3 桩身变形和受力分析

对C点(导管架顶部位移为0.2 m时)桩身挠度以及桩身应力进行分析。在导管架基础达到极限荷载时，上拔桩和下压桩的桩身挠度曲线基本一致，如图6a所示。两种桩的变形主要发生在泥面下深度7D的范围内，深部桩基本不发生变形，这是因为桩基础的桩径比约为17，均属于柔性桩。通过桩身应力图发现导管架基础上拔桩和下压桩出现最大桩身应力的位置大约在泥面下3D处，上拔桩应力约为下压桩的1.5倍，该处为桩最有可能发生破坏，如图6b所示。

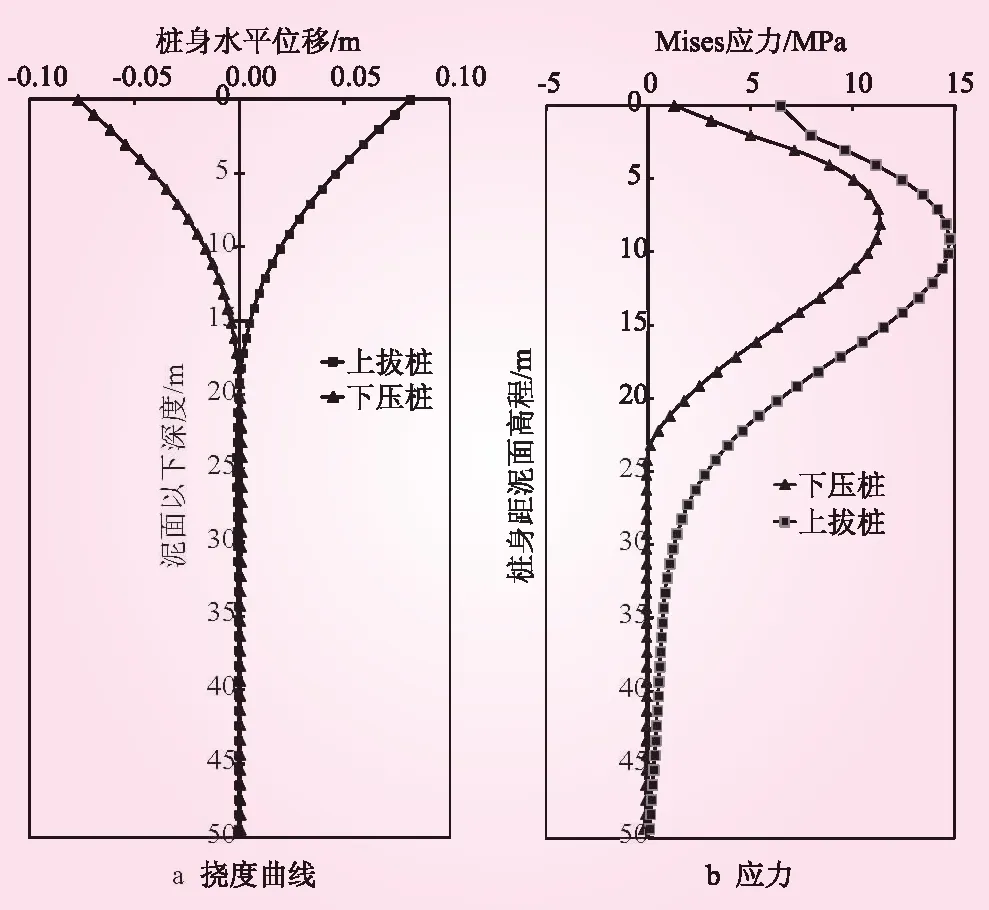
图6 桩身受力变形

4 结 论

采用ABAQUS对江苏某海域海上升压站四桩导管架基础水平承载性能进行数值模拟研究，得到如下结论：

(1)导管架基础水平荷载-水平位移(Q-s)特性曲线显示水平位移为0.2 m(C点)以后，水平承载力曲线基本保持不变，该四桩导管架基础的极限水平承载力为17 MN。

(2)在导管架基础达到极限荷载时，上拔桩和下压桩的桩身挠度曲线基本一致，两种桩的变形主要发生在泥面下深度7D的范围内，深部桩基本不发生变形。上拔桩和下压桩出现最大桩身应力的位置大约在泥面下3D处，该处桩最有可能发生破坏。

(3)当水平荷载较小时，上拔桩及下压桩的竖向位移与水平荷载呈线性变化；随着水平荷载逐渐增大，上拔桩开始出现上拔效应，当荷载逐渐接近导管架基础的极限承载力时，上拔桩竖向位移发生陡增现象，说明此时导管架基础已经发生失稳破坏。