BP神经网络在水库枯水季入库径流预报中的应用

崔立军

（唐山市陡河水库事务中心，河北 唐山 063021）

水库枯水季入库径流量受上游汛期降水量、汛末入库径流量和枯水季降水量等多因素影响，其准确预报一直是水库调度的难点和重要前提。当前预报方法很多，BP 神经网络由于具有高维性、自适应、自组织、自学习等优良特性，为复杂问题的解决提供了一条新途径，被广泛应用于水库枯水季入库径流预报中。

1 BP神经网络

BP 神经网络是一个高度的非线性映射，其结构如图1 所示，结构主要有输入层、隐含层和输出层等，假定N1、N2、N3分别表示输入节点、隐含节点和输出节点的个数，则BP 神经网络就是一个从RN1到RN3的映射，即：

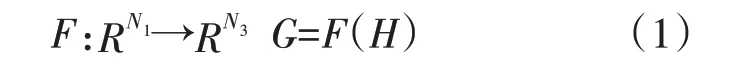
图1 BP神经网络结构

当前，已有多种不同性质、网络结构和作用（特性）的节点函数被应用到网络学习及径流预报中。本次选择BP型（Sigmoid）函数，其表达式为：

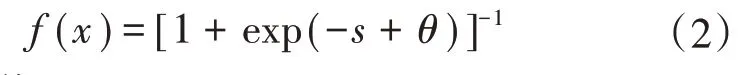
式中：θ为阈值。

图1 中输入节点作用是把输入传播给隐含层，节点输入与输出是相同的，换言之，对于第p 组样本，假定任一节点的输入为hip（i=1，2，…，N），输出为O，则有Oip=hip（i=1，2，…，N）。

对于隐含层第j个节点，其输入为：

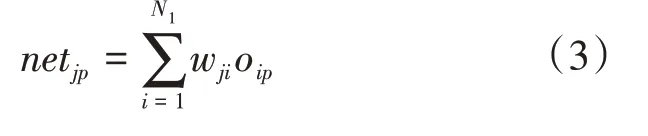
输出为：

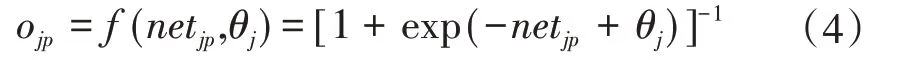
式中：netjp为第p 组样本对应隐含层第j 个节点的输入；Ojp为第p 组样本对应隐含层第j 个节点的输出；Wji为输入层第i 节点和隐含层第j 节点之间的连接权系数；θj为第j节点的阈值。

对于输出层第k 节点，其输入netkp和输出Okp分别为：

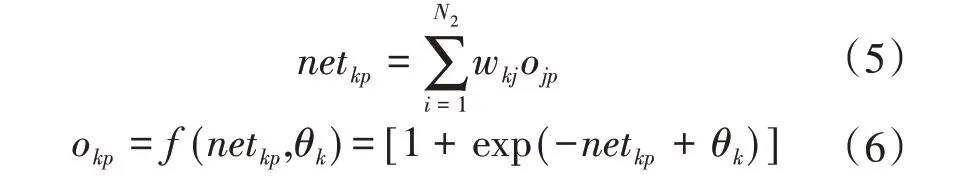
设第p 组样本期望的输出值为gkp（k=1，2，…，N3），其误差可以被认定为：

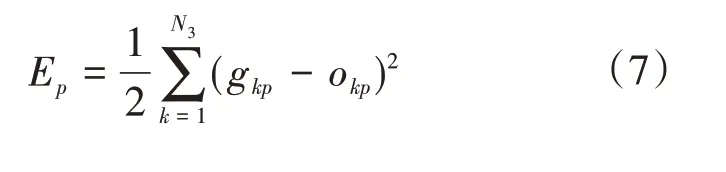
式中：Ep为第p 组样本期望的输出值误差；其余变量含义同上。

训练样本集的误差为：

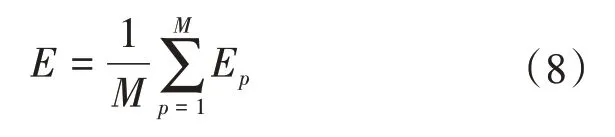
为使实际输出和期望输出尽可能接近，就要求E达到最小，可以利用下式修正连接权系数来实现：

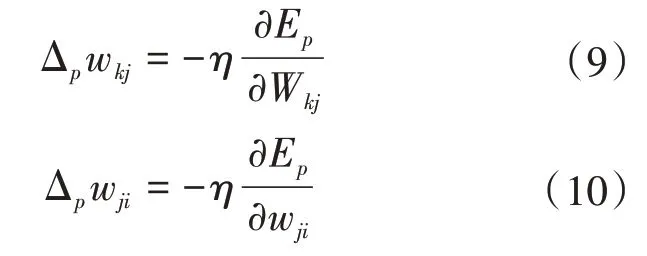
式中：η为学习率，取值范围为0～1；其余变量含义同上。其算法框图，如图2所示。

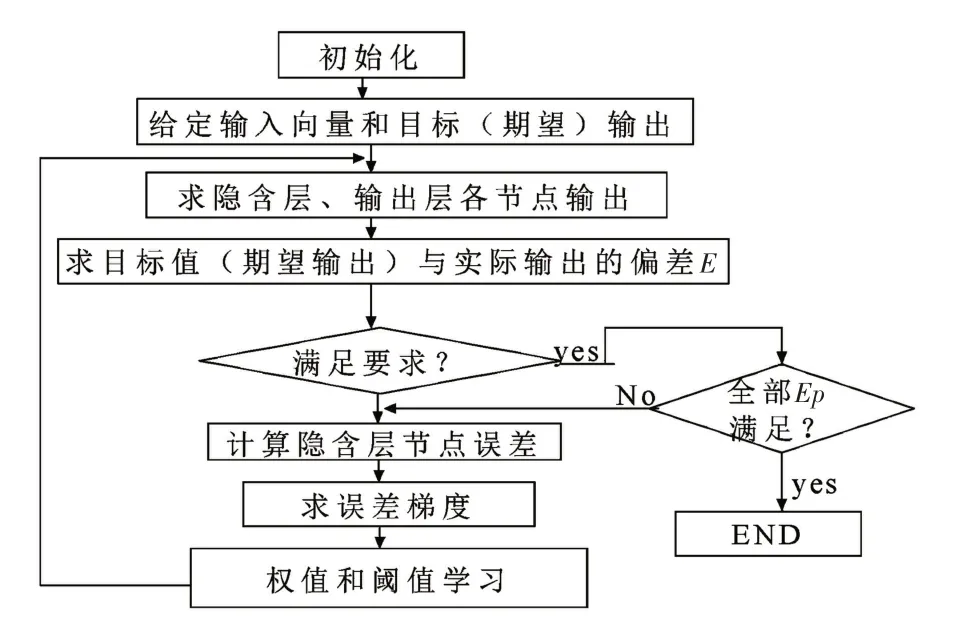
图2 BP算法框图

2 预报模型的计算步骤

步骤1：选定初始权向量WO，允许误差ε＞0，计算梯度向量gk的初始值g0，即g0=▽E（W0），令d0=-g0。

步骤2：给定迭代次数K。

步骤4：令Wk+1=Wk+akdk。

步骤5：计算新的梯度向量gk+1=▽E（Wk+1）。

步骤6：若kmod N=0，则重新开始，用WK=1代替W0，并返回步骤1。

步 骤7：计 算 误 差 因 子βk，即βk=[(gk+1-gk)Tgk+1]/(gk)2。

步骤8：计算新的共轭方向dk+1=-gk+1+βkdk。

步骤9：若E＞ε 或k≤K，则令k=k+1 转到步骤3；否则就将其停止，并把WK+1作为目标函数E 的最小值点。

式中：N为行向量W的维数；其余变量含义同上。

3 应用实例

选用河南省安阳市彰武水库作为研究对象，进行枯水季入库径流预报。

3.1 资料分析与预测因子选取

经过分析历史资料可知，彰武水库入流量主要有小南海水库下泄流量与小南海泉的涌水量两部分，而小南海水库下泄流量与小南海雨量站的实测降水量密切相关，所以本次预报将小南海泉的涌水量和小南海雨量站的实测降水量作为预测因子。

3.2 预报模型训练、结果及检验

3.2.1 样本选取

根据已知资料，训练样本选取1970—2004 年共35 a 径流系列，检验样本选取2005—2010 年共6 a的径流资料。

3.2.2 模型构造

根据预测的实际需要，首先构造具体结构如图3 所示的BP 网络模型Ⅰ，其输入层、隐含层、输出层节点数分别为2、5、2，利用小南海泉9月下旬平均涌水流量Q9x、小南海雨量站6—9 月降水量P6－9，预报彰武水库10—1、2—5 月径流量Q10－1和Q2－5。其次构造具体结构如图4所示的BP 网络模型Ⅱ，其输入层、隐含层、输出层节点数分别为3、5、1，利用小南海泉水文站9 月平均流量Q9、小南海雨量站6—9 月的降水量P6－9及1 月降水量P1，预报彰武水库2—5月径流量Q2－5。

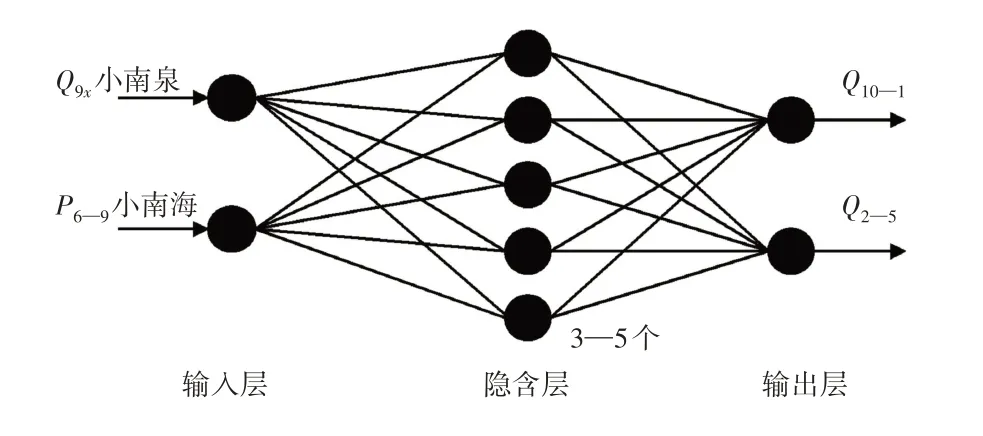
图3 彰武水库神经网络预测模型Ⅰ

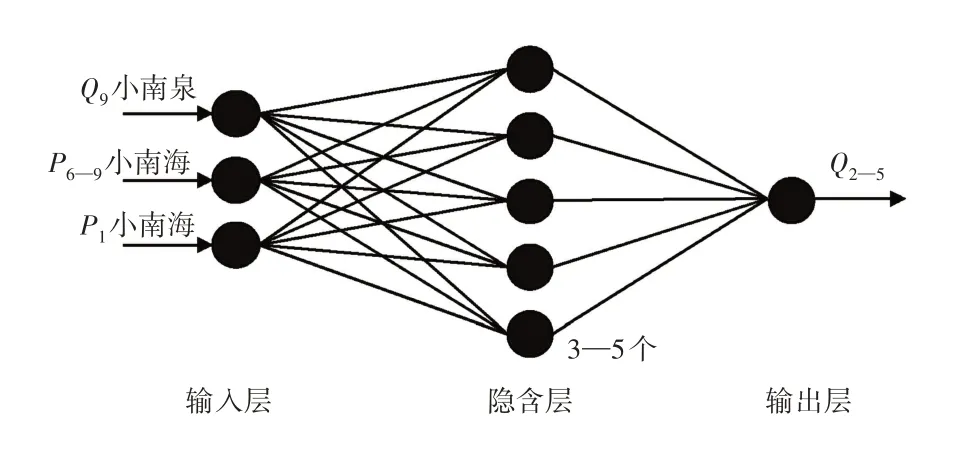
图4 彰武水库神经网络预测模型Ⅱ

3.2.3 预报结果

将已知的样本数据进行归一化处理，分别取学习率η=0.75、冲量因子α=0.90 和训练精度10-3进行模型训练并输入检验样本进行了验证，最后得到模型预报及检验结果，详见表1—2。

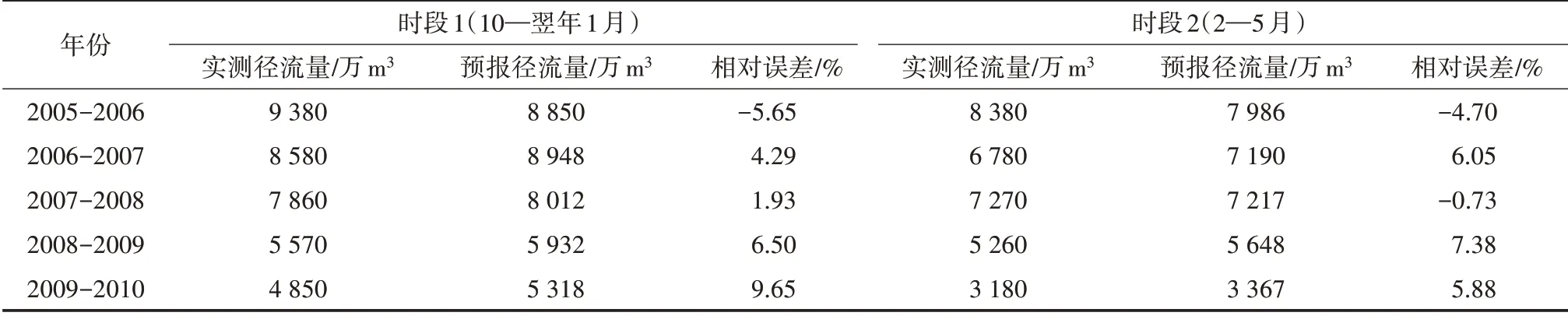
表1 BP网络模型Ⅰ预报结果

表2 BP网络模型Ⅱ预报结果

3.3 结果分析

从表1 及表2 可以看出，无论BP 网络模型Ⅰ还是BP网络模型Ⅱ预报彰武水库枯水季入库水量，检验误差合格率均为100%，预报精度高。

4 结论

神经网络具有其自身优良特性，为复杂问题提供了一条传统方法难以解决的新途径。通过预报实例表明，应用人工神经网络模型进行枯水季入库径流预报，误差小，精度满足要求。