基于ADMM方法的新增列车条件下灵活的列车时刻表优化算法研究
高如虎,牛惠民
(兰州交通大学 交通运输学院,甘肃 兰州 730070)
在高速铁路(以下简称高铁)运输组织中,当现有列车服务难以满足突发增长的客流需求时,需要在原有运营列车时刻表的基础上,规划新增列车的时刻表。对于新增列车条件下的时刻表优化是“列车运行调整”问题,但实质也属于列车时刻表优化范畴。列车时刻表问题(Train Timetabling Problem, TTP)是轨道交通领域中的经典问题。列车时刻表问题涉及数量众多的车站和列车,模型中所含决策变量数目随问题规模呈指数式增长,属于典型的NP-hard问题,很难在多项式时间内找到一种有效算法对其精确求解。尤其对于不同速度等级列车共线运行的情况,还需要处理列车越行时间和位置选择问题,使得问题更加复杂。如何设计可靠有效的求解方法,始终是列车时刻表问题的主要挑战[1-2]。
构建整数规划模型并利用商业优化软件求解列车时刻表问题,是近年来兴起的一种方法。文献[3-5]构建列车时刻表的混合整数规划模型,并利用优化软件CPLEX求解。文献[6]以总的乘客等待时间最少为优化目标,研究了时变客流需求条件下列车时刻表的优化问题,建立了带有线性约束的非线性整数规划模型并利用通用优化软件GAMS求解模型。不同速度等级列车共线运行情况下,还需要处理列车的越行问题,该情形改变了列车的发车顺序。因此,模型中除了列车到发时刻变量外,还需要表示列车发车顺序的0-1变量,这使得决策变量和约束条件的数量急剧增大[7-8]。而利用商业优化软件求解对数学模型要求苛刻,仅适合中小规模问题。
基于问题分解的求解方法,是解决列车时刻表问题的另一种有效思路,核心是将复杂的问题分解为容易求解的多个子问题,分别求解各子问题,然后通过集成和迭代,获得问题的最优解。近些年,很多文献利用拉格朗日松弛算法对复杂的列车时刻表问题进行分解并取得了显著的求解效果。文献[9]构建了基于时空图的时刻表整数规划模型,利用拉格朗日松弛算法将列车之间的耦合约束松弛,并分解为单列车在时空图中的最短路径子问题。文献[10]在研究城市轨道交通的列车时刻表问题时,考虑了能力和资源约束,最后利用拉格朗日松弛算法求解。文献[11]提出了基于累计变量的列车时刻表整数规划模型并设计了拉格朗日松弛算法求解。文献[12]研究了新增列车条件下的列车时刻表优化问题,并综合考虑了车站进路,利用拉格朗日松弛算法分解原问题。ADMM在拉格朗日松弛方法的基础上,通过引入增广项可快速的获得原问题的可行解。由于ADMM方法优越的分解性能,在大数据和机器学习领域[13]及分布式计算领域[14]被广泛使用。最近,文献[15]将ADMM方法应用到车辆路径优化问题,并提出了ADMM在交通运输组织优化领域的应用前景。文献[16]构建了基于扩展时空网络的周期性列车时刻表模型,并提出了基于ADMM方法的分解机制。
现有研究大多固定了列车的区间运行时间和列车停站方案或者为规划列车指定相对较小的出发时间窗,又或者固定了列车的发车顺序。本文以新增列车条件下的时刻表优化问题为切入点,创新点为:①为获得更高质量和更符合实际的列车时刻表,提出了更加灵活的列车时刻表设置方法。具体地,列车可灵活的选择区间运行时间、停站方案、停站时间、到发顺序、越行时机,此外,为规划列车赋予以小时为出发时段的更加灵活的出发时间范围。这种处理方法更加灵活,也更符合实际。②这种灵活的列车时刻表优化架构需要设计一种更加有效和更加科学的方法来解决列车对时空资源占用选择冲突问题。为此,本文提出了一种更加紧凑的基于时空弧段的不相容约束刻画列车的耦合约束。③分别利用标准的拉格朗日松弛方法和ADMM方法解决新增列车条件下的灵活列车时刻表优化问题,并对两种求解方法进行了比较,验证了ADMM方法在求解该优化问题时的优越性。
1 问题分析及说明
1. 1 问题分析
本文研究双线高速铁路新增列车条件下的时刻表优化问题。按照运输生产实际,铁路2个方向列车相互独立运行,选取其中一个方向进行研究。沿着该线路列车运行方向:U为车站集合;Ie为原有时刻表中列车集合;Ia为新增列车集合;[0,T]为全天运营时段,不失一般性,按照1 min为间隔对全天运营时段进行离散处理,以1 min的整数倍表示列车在车站的到发时刻和在区间的运行时间。
本文提出灵活的列车时刻表优化架构,主要有以下几方面的考虑:首先,铁路运营者往往按照小时客流需求推算运营列车数量,灵活架构下给定每个小时的列车数量与铁路运营实际相契合。其次,列车在线路区间运行速度并不固定,这种区间运行时间的灵活设置与铁路运营实际更加契合。然后,列车停站方案与列车时刻表关系密切,应该对二者进行综合设计。最后,传统的指定列车较小出发时刻范围的方法,事实上限制了列车对出发时刻的选择,并且相对固定了列车的出发顺序,此外,列车的出发时刻范围在实际中也很难确定。
事实上,在铁路运营实践中,这种灵活的列车时刻表优化架构相对于传统的列车时刻表优化更加贴合实际。理论上,这种灵活的优化方法相当于传统列车时刻表优化对列车出发时间窗、停站方案、停站时间以及列车发车顺序的松弛处理,此种处理能够获得更高质量的列车时刻表,但也无疑增加了列车时刻表优化的复杂度,需要设计一种更加有效的方法对其求解。
1.2 符号说明
本文通过构建时空网络描述列车时刻表问题,并据此建立基于时空弧段的0-1整数规划模型。以下给出用于构建网络和建立模型所需要的集合、索引、参数和变量。
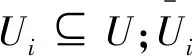
索引:i、j为列车索引,i、j∈I;u、u′为车站索引,u、u′∈U;t、t′、τ、τ′为时刻索引,t、t′、τ、τ′∈[0,T];(u,t)、(u′,t′)为时空网络节点索引,(u,t),(u′,t′)∈N;(u,t;u′,t′)为时空网络中从节点(u,t)到(u′,t′)的弧段索引,(u,t;u′,t′)∈A。
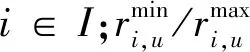
决策变量
xi(u,t;u′,t′)=

2 时空网络构建
由于列车时刻表固有的时空特性,构建时空网络模型是解决列车时刻表问题最常用的建模方式。通过构建时空网络,可将列车时刻表信息(如始发时刻信息、停站信息等)图形化地显示在网络结构中。此外,这种表现形式还可以将时刻表问题中难以描述的约束条件,转换为网络中弧段或节点的制约关系(如可达性、不相容性、网络流量守恒等),将优化目标转换为列车占用网络弧段的最小费用。G=(N,A)为时空网络,对每一个列车,都对应一个子网络。Gi=(Ni,Ai)为列车i对应的时空子网络,其中,Ni为列车i可占用的时空节点集合,Ai为列车i可占用的时空弧段集合。下面以列车i为例说明时空网络的构建过程,见图1。
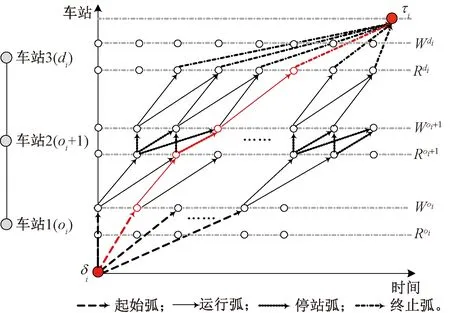
图1 时空网络图
2.1 网络节点
为保证时空网络的完整性,对列车i分别引入虚拟起点σi和虚拟终点τi。对于每个列车i∈I=Ie∪Ia,顶点Ni集合包含虚拟起点σi、车站到达节点集合Ru、车站出发节点集合Wu和虚拟终点τi。值得说明的是,对于原有列车i∈Ie,经过各个车站对应的起始节点和到达节点集合可由该列车原始时刻表、始发时刻最大偏移量、最小最大停站时间、最小最大运行时间确定;对于新增列车i∈Ia,经过各个车站对应的起始节点和到达节点集合可由出发小时时段、最小最大停站时间、最小最大运行时间确定。列车i的时空节点集合Ni可表示为
Ni={σi,τi}∪{Woi,Woi+1,…,Wdi}∪{Roi,Roi+1,…,Rdi}
2.2 网路弧段

列车占用弧段的费用见表1,α,β分别为原有列车和新增列车的费用权重。原有列车和新增列车对应的优化目标不同,对于原有列车,期望新优化的列车时刻表与原有时刻表的偏离程度越小越好,包括在始发站发车时刻的偏离以及区间运行时间、车站停站时间的偏离。而对于新增列车,期望总的旅行时间最小,包括区间运行时间以及在车站的停站时间。具体地,对于原有列车i∈Ie,起始弧的费用表示选择始发站的出发节点对应时刻与原列车时刻表始发时刻的偏差费用,运行弧和停站弧费用分别表征列车选择该运行弧段和停站弧段对应的运行时间和停站时间与原有时间的偏差费用。而对于新增列车i∈Ia,可在出发小时时段任意时刻出发,起始弧的费用为0。对于列车占用运行弧和停站弧的费用分别表征列车在区间的运行时间和车站停站时间费用。列车占用终止弧的费用均设置为0。列车从虚拟起点到虚拟终点对时空网络弧段的占用形成了一条时空路径(如图1红色线条所示),该时空路径反映了列车在各站的到发时刻信息。

表1 弧段费用
3 模型建立
3.1 优化目标
考虑到本文对列车区间运行时间、车站停站时间及新增列车出发时间窗灵活的设置,容许列车自由选择停站、越行时机、区间运行时间。这些因素直接决定了列车的旅行时间,进而影响铁路服务质量。因而,本文以新增列车的旅行时间最短为优化目标,同时我们希望原有列车的时刻表偏移量最小。通过时空网络的构建,列车时刻表问题转换为列车占用时空资源费用最小的网络优化问题,目标函数为
(1)
3.2 约束条件
(1) 网络流平衡约束
流平衡约束是网络优化问题最基本的约束。通过时空网络构建,在列车时刻表问题中,对于任意列车i,需要保证仅有一条时空路径被列车选择。流平衡约束为
(2)
(2) 列车停站约束
在原列车时刻表中,对于原有列车i∈Ie,若在u站停站,则在新优化列车时刻表中也必须在u站停站,该列车在其他车站可自由选择停站。对于新增列车i∈Ia,根据途径车站的类型,可分为两类情况,其中一类为必停站,此类车站一般为始发终到站及具有大客流的车站;另一类为备选停站,列车经过此类车站时,可自由选择是否停站及停站时间,此类车站一般为中间站及越行站。因此,列车停站约束可描述为
(3)
如果列车在某车站停站,则停站时间在最小和最大停站时间范围内自由选择。通过时空网络的构建,停站时间约束已经在时空网络停站弧中得到保证,这里再无需考虑。
(3) 安全间隔及越行约束
列车在时空网络中除满足上述的流平衡约束和列车停站约束外,还需要满足列车安全间隔约束。此类约束是多列车之间的耦合关系,为了保证列车对于时空资源占用的排它性,本文引入不相容弧集合描述。
为保证列车运行安全,任意两列车应满足安全出发间隔和安全到达间隔约束。此外,不同速度等级列车需要满足越行约束。事实上,列车安全到达间隔约束和列车越行约束均可转换为列车在车站应满足的出发间隔时间约束。为方便对列车安全间隔约束进行统一处理,本文引入不相容弧集合Φ(u,t;u′,t′),表示当某一列车占用时空网络运行弧段(u,t;u′,t′)∈Atravel时,其他列车不能同时占用时空网络中弧段的集合,即违反安全间隔的弧段。
给定某一时空弧段,则该弧段对应的不相容弧段集合也随之确定。具体地,对于时空运行弧段a=(u,t;u+1,t′)∈Atravel和b=(u,τ;u+1,τ′)∈Atravel定义:
ha,b=max{hdep,(t′-t)-(τ′-τ)+harr}
(4)
表示时空弧段a和b若同时被列车占用,应满足的安全间隔。
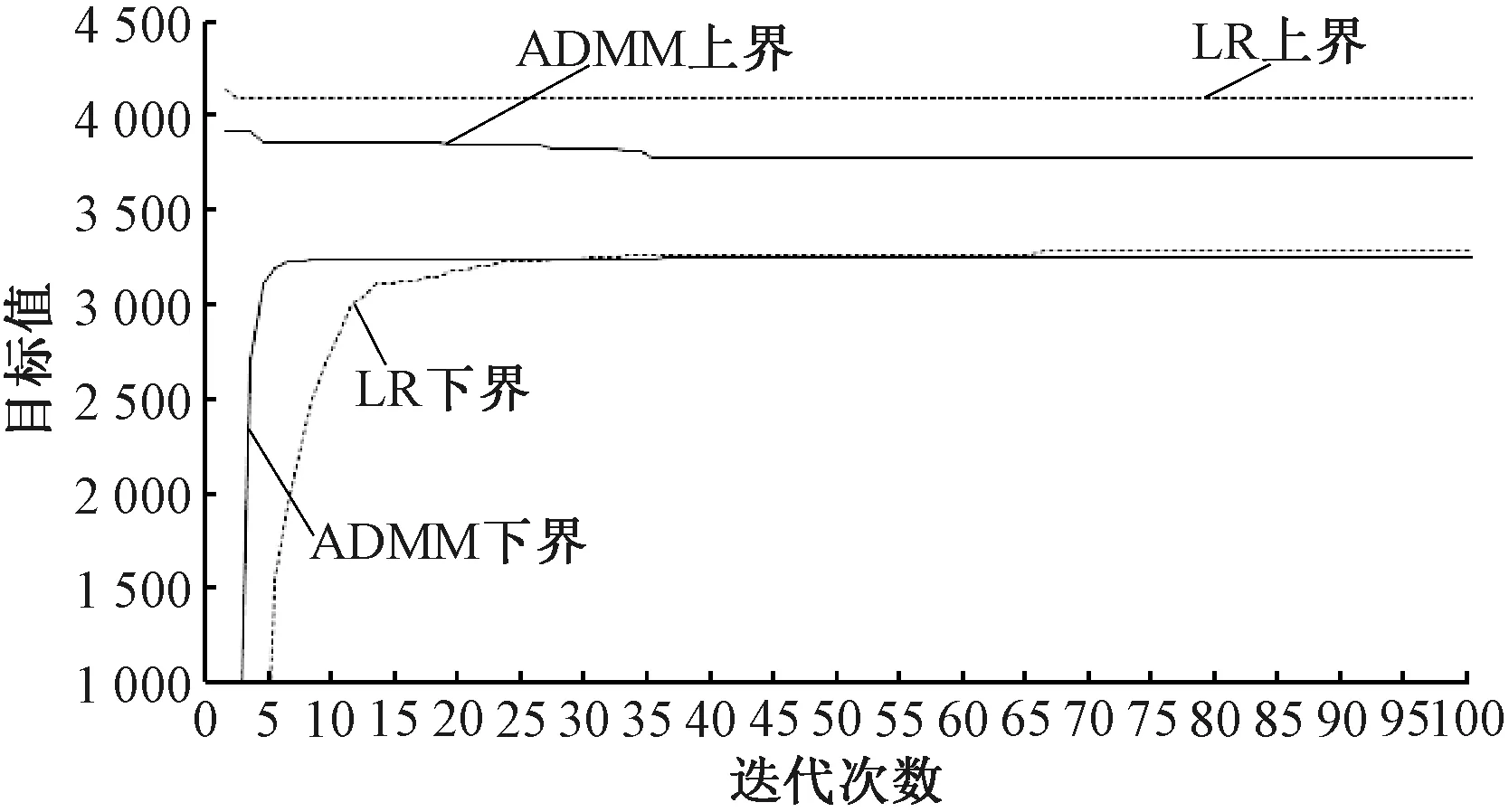
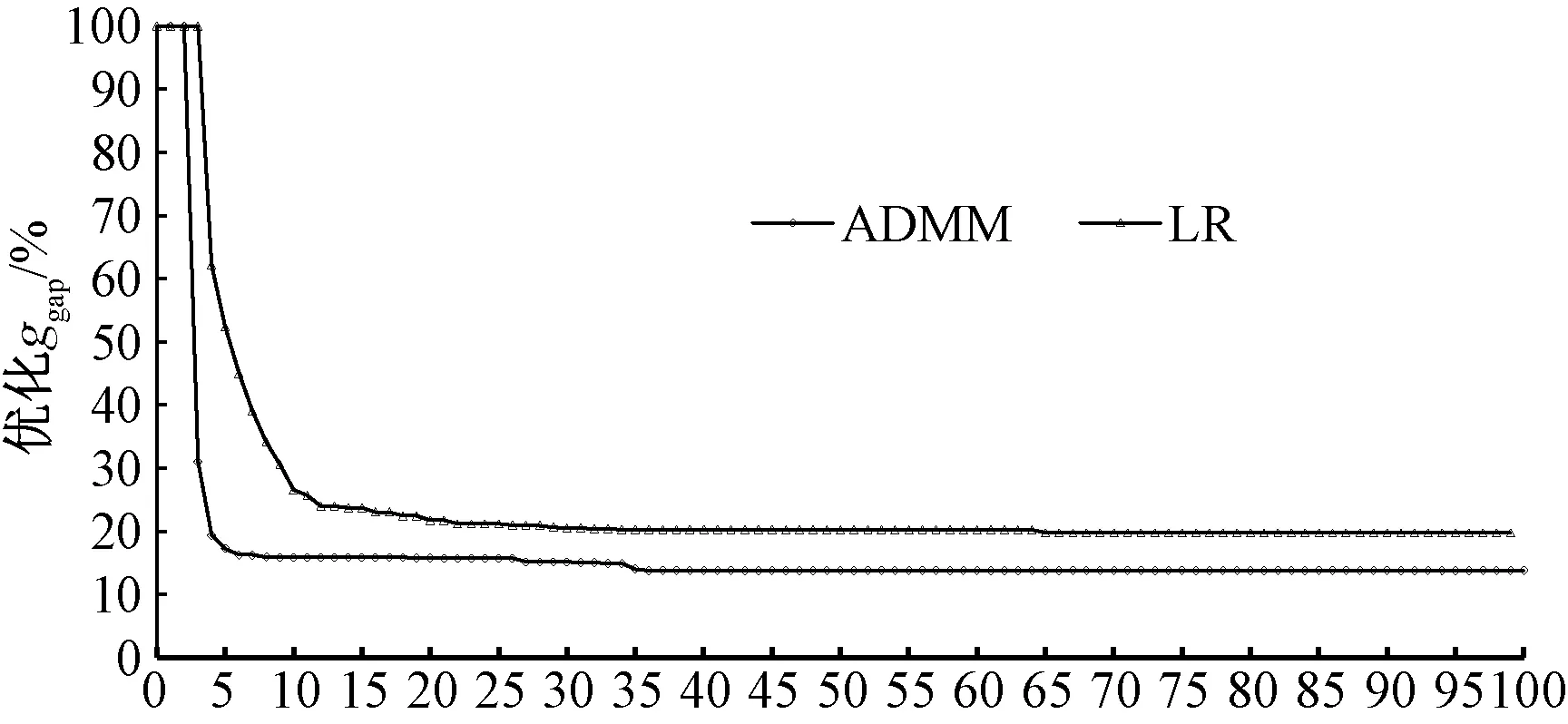
对于时空弧段a,如图2(a)所示,若t≤τ 对于时空弧段a,如图2(b)所示,若t-hb,a<τ 图2 不相容弧示意 综上所示,弧段a的不相容弧集合Φ(a)为 Φ(a)={b=(u,τ;u′,τ′)∈Atravel|t-hb,a< τ (5) 对于任意的时空运行弧段a,在不相容弧集合Φ(a)内,当有列车占用时空网络弧段a时,其他任意列车不能占用不相容弧集合Φ(a)内的其他弧段。不相容约束可描述为 ∀i∈Ia∈Atravel (6) 下面分两种情况讨论不相容约束: (4) 变量域约束 xi(u,t;u′,t′)∈{0,1} ∀i∈I(u,t;u′,t′)∈Ai (7) 本文所建立模型中的约束条件式(6)为多列车耦合约束,下面利用拉格朗日松弛算法对列车时刻表模型进行松弛和分解。具体地,引入非负的拉格朗日乘子λi(a)≥0,∀i∈I,a∈Atravel,将模型中的耦合约束条件松弛,形成拉格朗日对偶问题。拉格朗日函数为 (8) 进一步地,拉格朗日函数可被整理为 (9) 其中 (10) 移除式(9)中的常数项,原问题被分解为如下的单列车子问题 (11) s.t. 式(2)、式(3)、式(7)。 子问题为单列车在时空网络中的最短路径问题,可利用最短路径算法快速求解。在拉格朗日松弛方法中,通过迭代求解子问题,并更新拉格朗日乘子可获得原问题的下界。 在迭代求解时,使用次梯度法更新拉格朗日乘子。 (12) ηq=1/(q+1) (13) 拉格朗日松弛算法如下所示: Step6终止条件。如果ggap≤ε(最小gap值) 或者q>Q(最大迭代次数),则算法终止;否则,令q=q+1,返回Step2。 在求解子问题时,如式(10)所示,列车的最短路径费用取决于时空弧段的旅行时间费用ci(a)和拉格朗日乘子λi(a)。在每次迭代时,仅通过列车占用弧段的拉格朗日乘子值调节列车的路径选择。事实上,在拉格朗日松弛方法迭代过程中,当所有列车时空路径选择完成后,才统一更新各弧段的拉格朗日乘子值,相当于在一次迭代时同一小时内的同等级列车占用弧段的拉格朗日乘子也相等。这就导致了在每次迭代时,同一小时内的同等级列车会选择同样的时空最短路径。这种解的对称性问题严重阻碍算法的效率。 ADMM方法适用于可分结构的凸优化问题,可将原问题等价的分解成易求解的子问题,交替求解子问题,以获得原问题的最优解或者可行解。ADMM方法是在拉格朗日松弛方法的基础上引入二次惩罚项,构造增广拉格朗日函数,将原问题分解成若干个容易求解的子问题;在次梯度迭代的过程中,按照一定次序对不同的变量进行交替迭代求解,最终得到最优或可行解。 根据ADMM原理,首先引入松弛实数变量di(a)∈[0,1],将耦合约束不等式(6)转化为等式 (14) 对于本文所建立数学模型,在拉格朗日松弛函数的基础上,引入二次惩罚项ρ,构造增广拉格朗日函数 (15) 增广拉格朗日函数中含有二次项,使得问题失去了可分解性。下面对增广拉格朗日函数进行线性化处理,令 (16) [di(a)+pi(a)-1]2} (17) 显然,由于存在松弛变量di(a),上式中还存在二次项,下面确定松弛变量di(a)的取值。将上式中除松弛变量di(a)以外的其他变量看成为参数,并将与松弛变量di(a)相关项组合为如下的二次函数形式 Ldi(a)=di(a)2+2×di(a)×[pi(a)-1+xi(a)+ (18) 式中:Q为与松弛变量di(a)的无关项。由于松弛变量di(a)为连续变量,因此,函数Ldi(a)取最小值的点为 (19) 下面分两种情况进行讨论松弛变量di(a)的取值: (1) 当pi(a)≥1时,则di*(a)≤0,并且在[0,1]范围内,函数Ldi(a)为递增函数。故最优的d*(a)=0,带入公式(18),二次项可转化为 xi(a)+2×[pi(a)-1]2 (20) 综合两种情况,增广拉格朗日问题可进一步分解为如下的单列车的子问题 (21) s.t. 约束式(2)、式(3)、式(7)。 其中, (22) 本文研究的列车时刻表问题含有关于多个列车的多个决策变量,将ADMM方法扩展为多块(multi-block)的情况。值得说明的是,标准的two-block ADMM 方法的收敛性已经被证明[17]。而扩展的multi-block ADMM 方法被通过反例证明并不必然收敛[18]。尽管没有收敛性的保证,但由于multi-block ADMM 方法的可操作性及高效性,在一些实际的优化问题中却被广泛应用[19]。 通过对原问题进行松弛、增广、线性化和分解求解方法的设计,利用ADMM方法求解列车时刻表的具体流程如下所示。 Step2基于优先权迭代顺序产生ADMM解。 For 每个列车i∈I 最短路径算法求解i列车对应的ADMM子问题Lρ,i; 固定列车i对应子问题的解; Endfor Step6终止条件。如果ggap≤ε(最小gap值) 或这q>Q(最大的迭代次数),则算法终止并令上界解作为最后输出结果;否则,令q=q+1,返回Step2。 值得说明的是,算法中Step2拉格朗日乘子和二次惩罚项的更新参考了文献[15]中的方法。算法中Step3的启发式可行算法与拉格朗日松弛算法中的启发式可行算法相同,可利用文献[11]中提出的优先权算法求解。 以武广高铁线路为例,此线路包含18个车站,为方便描述,车站依次编号为1~18。在此线路上运行两种速度等级的列车,不同速度等级列车在区间的运行时间见表2。高等级列车最小/最大停站时间分别为2、5 min,低等级列车最小/最大停站时间分别为2、10 min。线路上在全天规划时段06:00—24:00内,原有列车135列,计划新增列车20列。为便于处理,假定原有列车均为高等级列车,新增列车均为低等级列车,假定列车在区间的运行时间为常数。原有列车的始发站出发时间最大偏移量为10 min,关于新增列车的相关运营参数见表3。本文所提出的算法在Visual Studio 2013平台上使用C++语言实现,算法运行环境为1台CPU Intel Core i5-4 590 s 3.00 GHz, 4 GB内存的个人计算机。 表2 列车在线路区间的运行时间 表3 新增列车相关运营参数 分别利用标准的LR和ADMM算法求解,共迭代100次,两种算法对应的上下界迭代过程见图3,对应的优化ggap值变化情况见图4。对于ADMM方法,最优的上界为3 774,最优下界为3 254,最优ggap值为13.78%,计算时间为302.74 s;对于LR算法,最优的上界为4 097,最优下界为3 287.33,最优ggap值为19.76%,计算时间为195.83 s。从两种算法的迭代过程及计算结果中不难看出,尽管ADMM方法的计算时间略大于LR方法,但求得的最优上界和ggap值更优。此外,ADMM方法收敛的速度比LR算法更快。因此,对于本文优化的新增列车条件下的灵活列车时刻表优化问题,ADMM相比于LR具有更好的计算性能。 图3 LR和ADMM算法的上下界迭代过程 图4 LR和ADMM算法的ggap迭代过程 利用ADMM方法优化的列车运行图见图5。限于篇幅,对应的列车时刻表(整数形式,如0对应06:00,依次类推)上传至https:∥github.com/ruhugao/Ahu。从运行图中可以看出,部分新增的低等级列车可被原有的高等级列车越行,如新增的从武汉站开往广州南站的列车1分别在郴州西和韶关站被原有高等级列车越行;部分原有列车改变了原有的列车时刻表,如原有列车4在其始发站武汉站的出发时刻为07:33,优化后的出发时刻调整为07:37。部分新增列车除了在计划的列车车站停站外,在其他车站也可停站,可以在最小和最大停站时间之间灵活的选择停站时间,如新增列车1在计划之外的郴州站停站4 min。本文提出的这种灵活架构下,利用两种分解算法求解时,可以迅速的得到可行解。 图5 优化的列车运行图 本文针对新增列车条件下的高速铁路列车时刻表进行优化。为了获得更高质量的列车时刻表,提出了一种灵活的列车时刻表优化架构。通过构建时空网络的手段,建立了基于时空弧段的0-1整数规划模型,提出了一种更加紧凑的不相容约束用以刻画列车时刻表优化问题的列车安全间隔约束。分别利用标准的拉格朗日松弛方法和交替方向乘子法对原问题进行分解和求解,并以武广高速铁路线路为例进行了实例分析。研究结果表明: (1)相对于传统的列车时刻表优化问题,在灵活的列车时刻表优化架构下,更能够快速的获得可行的列车时刻表。 (2)本文提出的更加紧凑的基于时空弧段的不相容约束能够更加清晰的刻画列车之间的耦合关系,同时这种不相容约束在ADMM方法对原问题分解过程中也更加方便。 (3)通过实例验证,利用标准的拉格朗日松弛方法求解的最优ggap值为19.76%,而利用ADMM方法求得的最优ggap值为13.78%。两种方法相比,尽管ADMM方法的计算时间略大于LR方法,但求得的最优上界和最优ggap值更优。此外,ADMM方法收敛的速度比LR算法更快。
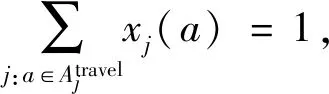

4 基于拉格朗日松弛的分解
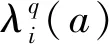
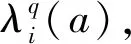
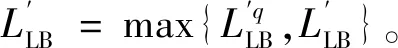
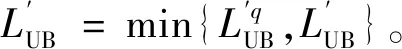


5 基于ADMM的求解方法
5.1 基于ADMM的松弛、增广和分解
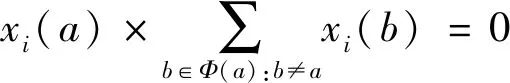

5.2 基于ADMM方法的求解过程
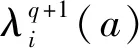
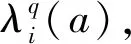
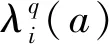
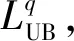
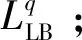
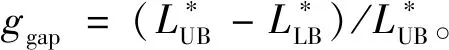
6 算例



7 结论

