“k、b”怎样“控制”一次函数图像
丁锦荣


我们知道,在平面直角坐标系中,一次函数的图像是一条直线,这条直线的位置是怎样确定的呢?这与一次函数的解析式y=kx+b(后≠0)有关,具体来说,就是与k、b有关。对于一次函数的解析式y=kxx+b(k≠0),k、b的取值“控制”着一次函数图像(直线)在平面直角坐标系中的位置。
我们先结合例1,来看看后、6的取值是怎样对一次函数图像进行“控制”的。
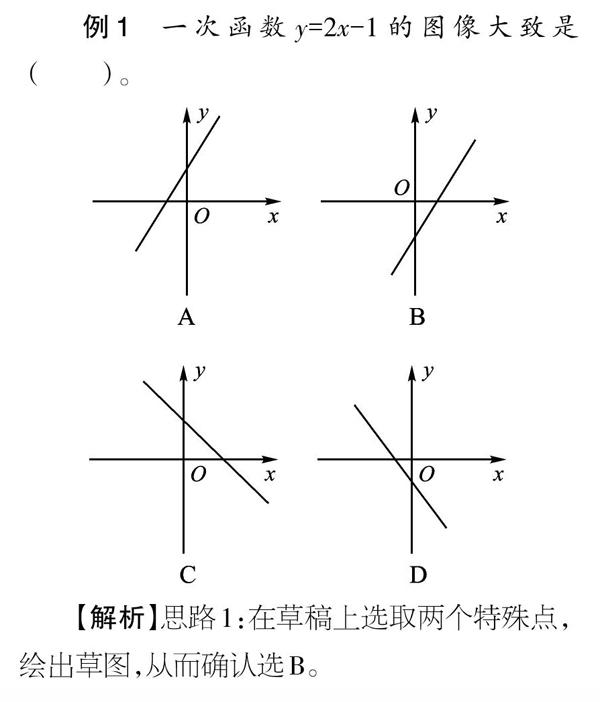
例1 一次函数y=2x-1的图像大致是( )。
【解析】思路1:在草稿上选取两个特殊点,绘出草图,从而确认选B。
思路2:从一次函数解析式中k、b的特点出发,判断一次函数图像的大致位置。k为正数时,一次函数图像呈上升走势,排除C、D;b是负数,说明一次函数图像与y轴的交点在其负半轴上,排除A,选B。
【总结】对于这个例题,思路1看起来是比较简洁的方法。但我们也应该关注和理解思路2,因为它回答了一般情形下一次函数图像与k、b的关系。为了更清楚地表述,我们列表如下:
现在我们再来看几个与之相关的例题。
例2 一次函数y=-x-1不经过的象限是( )。
A.第一象限
B.第二象限
C.第三象限
D.第四象限
【解析】与例1-样,我们也有两种思路可供选择。借用刚才的表格,结合k<0且b<0,我们可以发现函数草图应该为图6的走势,所以选A。
【总结】这类问题是一次函数的经典考题。一般解法是由k、b的取值确定大致图像或由图像确定k、6的取值范围。我们应结合图像来理解记忆,其中k决定图像上升或下降的趋势,b决定图像与y轴的交点位置。同学们注意体会这里的“数形结合”思想。
例3如图7,直线AB对应的函数表达式是( )。
A.y=一3/2x+3
B.y= 3/2x+3
C.y=-2/3x+3
D.y= 2/3x+3
【解析】乍一看,我们還没学过怎样确定一次函数解析式,怎么办?同学们别急着下结论。选择题不是填空题,我们不会直接求解,可以去排除选项。4个选项的解析式都是明确的,我们看看谁的函数图像符合图形就可以了。根据k、b的正负,选项A、C都符合,但A的一次项系数不符合要求,所以选C。
【总结】随着学习的深入,我们还有更一般的方法。但是就选择题来说,这里根据k、b的特点运用的排除法仍是最优的方法。
例4 点Pl (XI.Yi)、P2 (X.,y2)是一次函数y =-4x+3图像上的两个点,且x1
A.y1> y2
B.y1> y2>0
C.y1
D.y1=y2
【解析】由一次函数y =-4x+3的k=-4<0,6=3>0,可知函数值y随x的增大而减小,即当x1y2。故选A。
【总结】本题要结合一次函数系数特点,识别其图像的增减性,以确定函数值的大小关系,是一类经典题型。同学们需要注意,本题不能(也不需要)确定函数值y1、y2与0的关系。
(作者单位:江苏省海安市城南实验中学)

