平面直角坐标系中“点的运动”

哥特

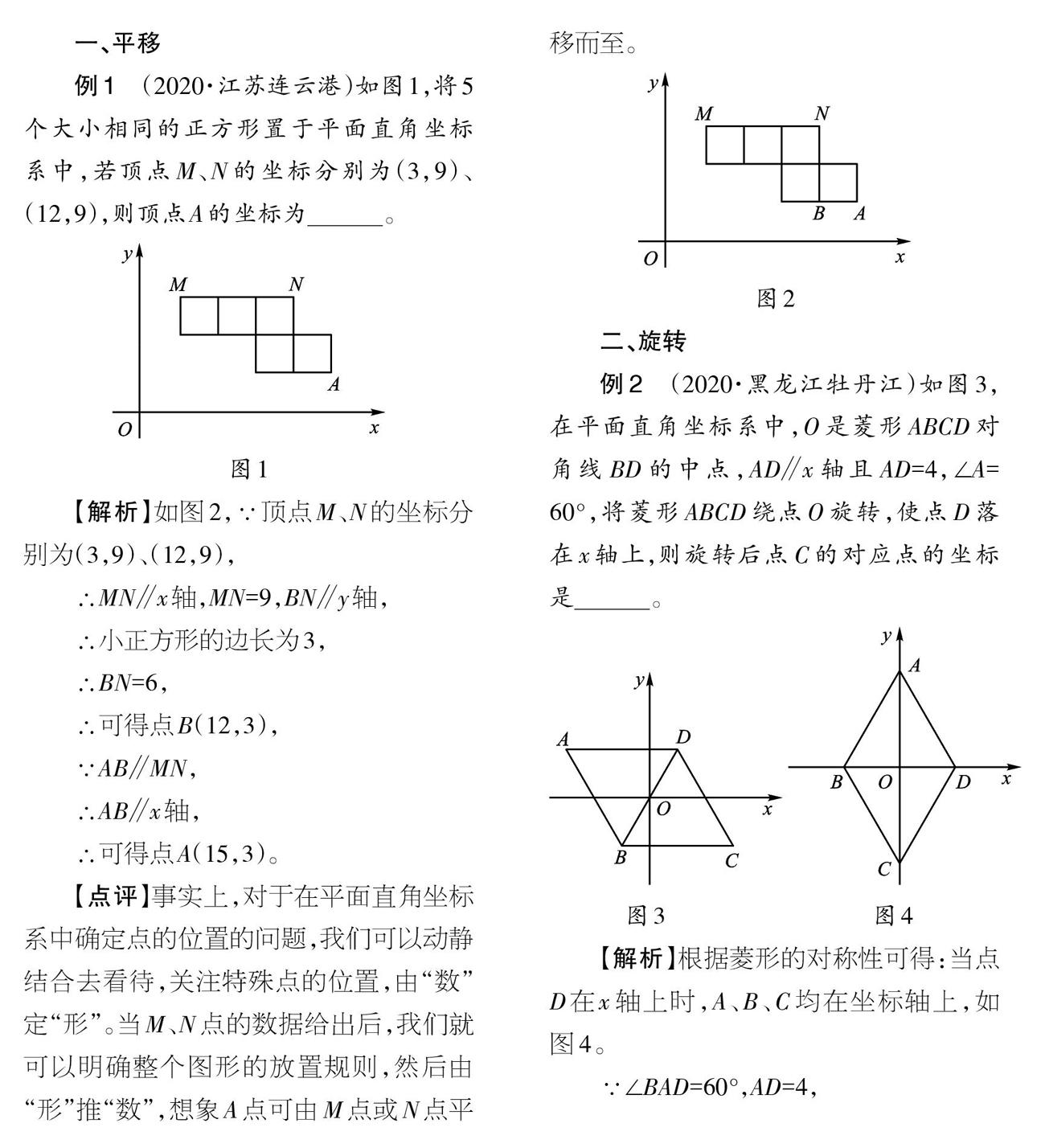
例1 （2020.江苏连云港）如图1，将5个大小相同的正方形置于平面直角坐标系中，若顶点M、N的坐标分别为（3，9）、（12，9），则顶点A的坐标为_____ 。

【解析】如图2，∵顶点M、N的坐标分别为（3，9）、（12，9），

∴MN//x轴，MN=9，BN//y轴，

∴小正方形的边长为3，

∴BN=6.

∴可得点B（12，3），

∵AB//MN，

∴AB//x轴，

∴可得点A（15，3）。

【点评】事实上，对于在平面直角坐标系中确定点的位置的问题，我們可以动静结合去看待，关注特殊点的位置，由“数”定“形”。当M、N点的数据给出后，我们就可以明确整个图形的放置规则，然后由“形”推“数”，想象A点可由M点或Ⅳ点平移而至。

二、旋转

例2（2020.黑龙江牡丹江）如图3，在平面直角坐标系中，O是菱形ABCD对角线BD的中点，AD//x轴且AD=4，∠A=60°，将菱形ABCD绕点D旋转，使点D落在x轴上，则旋转后点C的对应点的坐标是

。

【解析】根据菱形的对称性可得：当点D在x轴上时，A、B、C均在坐标轴上，如图4。

∵∠BAD=60°.AD=4.

【点评】本例中，由特殊四边形和特殊角的条件出发，明确点的起始位置;然后借助旋转的运动方式，确定C点的最终位置，注意还要分类哦。

三、翻折和缩放

例3 （2020.宁夏）在平面直角坐标系中，△ABC的三个顶点的坐标分别是A（1，3），B（4，1），C（1，1）.

（1）画出△ABC关于x轴对称的△A1B1C1;

（2）画出以点O为位似中心，与△ABC位似比为1：2的三角形。

【解析】（1）分别作A、B、C关于x轴的对称点A1、B1、C1，连接A1C1，A1B1，B1C1，得到△A1B1C1。

如图6所示，△AiBlCl即为所求。

（2）已知位似中心是原点。特别提醒一下，对于“位似”的知识点，需要判断图形是放大还是缩小。这里两个都可以，同学们要注意。以放大为例，则分两种情况：

第一种，要求的三角形和△ABC在坐标轴的同一侧。

第二种，要求的三角形在△ABC的对侧。

如图6所示，△A282C2和△A383C3即为所求。

同学们可以自己尝试探索其他情形。

【点评】在有网格背景的平面直角坐标系中，点的运动可以被刻画得更精准。本例和之前例题中的单一要求有所不同，它可以看作是点的翻折和缩放这两个运动的结合。

（作者单位：江苏省太仓市实验中学）