一种用于直接射频采样ADC 的多模式数字下变频器设计

彭庆尧 吴旦昱 *周 磊武 锦刘新宇

(1.中国科学院微电子研究所，北京 100029；2.中国科学院大学微电子学院，北京 100049)

直接射频采样模数转换器(Analog-to-Digital Converter，ADC)是直接射频采样接收机的关键组成部分，通常具有高速、高精度、高采样率的特点。但由于受到数字信号处理技术与微电子技术发展的限制，后续的数字信号处理器(Digital Signal Processor，DSP)难以对ADC 采样得到的数据进行实时处理[1]。为了解决高速ADC 与低速DSP 之间的矛盾，就需要对采样后的信号进行预处理[2]。数字下变频器(Digital Down Converter，DDC)是一种为解决这种矛盾而诞生的电路[3-4]。如图1 所示，在射频采样接收机中，DDC 通常位于射频采样ADC 与DSP之间，它的功能是降低信号的中心频率、降低信号的采样率与过滤高频噪声[5]。

图1 直接射频采样接收机

同时，多抽取模式的DDC 也是需要关注的。随着无线通信技术的发展，载波带宽种类繁多。针对无线通信中各种应用场景，具有多种抽取模式的DDC可以很好地应用于这些场景和多种载波带宽，节省后端DSP 的计算资源，降低系统功耗和成本[6-8]。

本文在深入研究了多种DDC 的实现方案后，提出了一种多模式DDC 结构，并基于28 nm 工艺将其内嵌于ADC 中，实现了DDC 的GDSII 版图设计。与前人设计相比，本设计优化了电路结构，提高了抽取滤波器的工作时钟频率，实现了14 种抽取模式，能够实现较高的阻带衰减。

1 电路结构

本文设计的DDC 整体结构如图2 所示。输入信号经过正交混频后，分别通过I＼Q 两路抽取滤波器组进行抽取和滤波后输出。设计中包含一个数控振荡器(Numerically Controlled Oscillator，NCO)，用于产生混频所需的正弦波与余弦波。I＼Q 两路信号分别经过抽取滤波器组完成低通滤波与抽取，滤波器组可以构成14 种不同的抽取模式以适应不同场景下的应用需求。

图2 DDC 整体结构

1.1 数控振荡器

NCO 用于对输入的信号混频，需要产生最大fs/2频率的正弦波，并能够对产生正弦波的频率与相位进行控制。本文设计的NCO 结构如图3 所示，包含相位累加器、相位寄存器、相位偏移器和相位振幅映射器。前三个部分通过累加频率控制字并叠加一个初始相位产生当前相位；相位振幅映射器将当前的相位映射到相应的振幅。

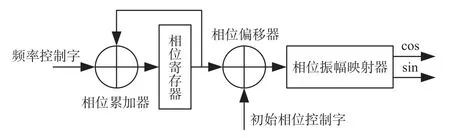
图3 NCO 结构

常见的相位振幅映射器有使用只读存储器(Read-Only Memory，ROM)查找表的方法和基于坐标旋转数字计算法(Coordinate Rotation Digital Computer，CORDIC)的方法。基于ROM 查找表的方法，预先将计算好的振幅值存在ROM 中，使用时根据相位值查找对应的振幅值[9]。采用这种方法设计的相位振幅映射器原理简单易实现，但输出精度完全依赖于ROM 的数据位宽，另一方面，输出信号的频率下限越低，意味着输出振幅的精度越高，则所需要的ROM 容量越大。因此基于ROM 查找表的方法不可避免地会占用大量的面积。基于CORDIC 的方法对向量旋转进行迭代，通过逼近目标角度来计算得出正余弦值。这种方法只用到了加法与移位运算，同时使用流水线结构，因此可以在输出精度足够的情况下，保持较高的采样率，也不会受到ROM 容量的限制[10-11]。本文采用了基于CORDIC 算法实现的数控振荡器，通过增加流水线加法器在保持1 GHz 工作时钟频率下，增加了数据精度，实现了较高的无杂散动态范围。

1.2 抽取滤波器组

信号经过混频后，频谱被搬移至基带。此时，信号频谱附近的噪声也被搬移至基带附近，同时基带信号仍保持着较高的采样率。抽取滤波器组的目的就是滤除噪声，同时降低基带信号的采样率。

随着无线通信技术的发展，载波带宽种类繁多。针对无线通信中的多种应用场景，DDC 也需要提供多种下变频模式。文献[7]通过级联多个二抽取滤波器，在不同的情况下旁路掉不需要的抽取滤波器实现了多种抽取模式，这种设计因结构简单而常被采用，但能够实现的抽取模式较少，且只能实现2 的幂次方倍抽取。为了实现多种下变频模式，本文设计了若干具有不同系数的滤波器，在不同应用情况下，通过多路选择器选通不同的滤波器与抽取率的组合。

多模式滤波器组抽取功能的实现方式有两种，一种方法是所有电路都工作在主时钟下，通过计数器产生有效信号来告知下级电路哪一时刻的数据是有效的。这种方法设计思路简单，代码上易于实现，但在实际应用中所有电路都工作在主时钟下，翻转率高会导致动态功耗过高，所有时序电路都约束在高速的主时钟下也会为后端综合与设计带来困难。另一种方法是通过时钟分频产生全部所需的时钟信号，提供给对应的抽取滤波器。使用这种方法，越靠后的抽取滤波器必然会工作在速度越低的时钟下，减少了动态功耗；另一方面，在不使用某些抽取滤波器时，时钟管理模块提供给该滤波器的时钟拉低，使该模块不工作从而消除了短路功耗，进一步减少整体电路功耗。滤波器组结构如图4 所示，时钟管理模块产生主时钟与主时钟的2～48 分频时钟，分别为clk1、clk2～clk48，根据不同情况下的滤波器配置，提供给每个滤波器对应的输入时钟和输出时钟。图5 为抽取系数为48 时滤波器组结构与时钟配置。

图4 滤波器组结构与时钟配置

图5 抽取系数为48 时滤波器组结构与时钟配置

2 电路设计

2.1 CORDIC 算法与流水线实现

CORIDC 算法的核心思想是“二分法逼近”。通过预设一组特定的角度，计算时，逐次旋转这些角度，最终逼近目标角度，并在每次旋转中进行计算，最后得到目标角度的正余弦值。

当图6 中A向量旋转到B向量时，有等式(1):

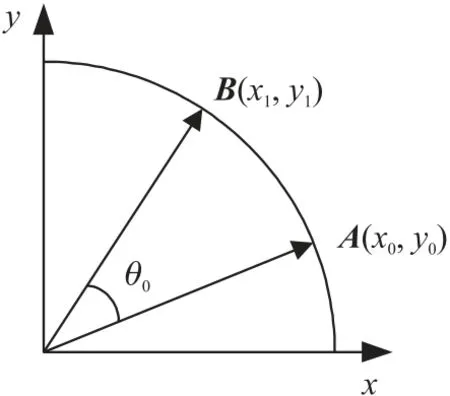
图6 向量旋转示意

则第i次旋转时，将等式转化为矩阵形式，有等式(2):

提取出公因式cosθi-1后得到等式(3):

化简计算，可以令tanθi＝2-isi，利用二进制的运算法则将乘法运算转换为移位运算。其中si为tanθi的符号，也代表着旋转的方向。若从x轴处，也即x0＝1，y0＝0 处开始逆时针旋转，每旋转一次θi后检测当前角度与目标角度的差距，若不足则继续逆时针旋转，若超出则顺时针旋转。累计旋转n次后，有等式(4):

在等式的基础上，加入z0＝θ，zi＝zi-1-si-1θi-1，其中θ为需要计算正余弦值的目标角度，依据此设计出流水线结构如图7 所示。

图7 CORDIC 算法的流水线结构

2.2 多模式抽取滤波器组

2.2.1 单级滤波器与抽取

和无限冲激响应(Infinite Impulse Response，IIR)数字滤波器相比，有限冲激响应(Finite Impulse Response，FIR)数字滤波器线性相位延迟，且由于极点全部在原点，运行更加稳定。FIR 数字滤波器的缺点是设计复杂，但可以使用计算机辅助设计。借助MATLAB 的Filter Design ＆ Analysis 工具，就可以快速准确地得到目标滤波器的阶数与抽头系数。考虑到系统稳定性和实现更大的信噪比与无衰减通带带宽，本文采用了级联FIR 滤波器的方案。

为实现降低采样率的功能，信号还需要经过抽取。D倍抽取一般指每D个信号抽出一个信号，其余舍弃，D为整数，称为抽取因子。信号经过D倍抽取后，采样率变为原来的1/D，同时信号的频谱发生周期性拓展。根据奈奎斯特采样定理，采样率需要大于信号最大频率的两倍，否则会发生混叠导致信号失真。

N抽头FIR 数字滤波器的差分方程为式(6):

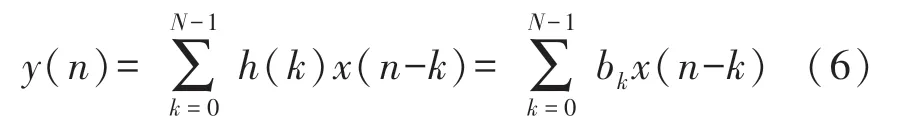
式中:bk为单位冲激响应h(n)的序列值。对于有限冲激响应数字滤波器，bk包含有限个非零值。设计中采用了半带(Half-band，HB)FIR 滤波器，HB FIR滤波器的特征是滤波器的幅频响应关于1/4 采样频率对称，通带波纹与阻带波纹相等。这些特征决定了滤波器的抽头数为奇数个，bk中有接近一半的值为零，且抽头系数具有对称性如式(7)所示。

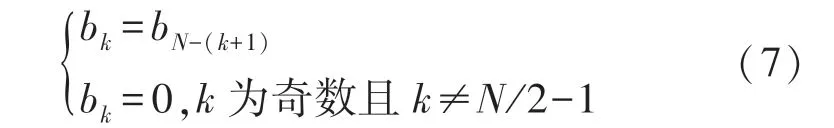
根据这些特性，系数为零意味着可以省去接近一半的乘法器；系数对称意味着可以通过提取公因式的方法，将先乘后加的计算顺序改变为先加后乘，再减少接近一半的乘法器。这种选择可以优化滤波器结构，减少加法器与乘法器的数量，节省消耗的电路资源。因此，N抽头HB FIR 滤波器的差分方程为式(8):

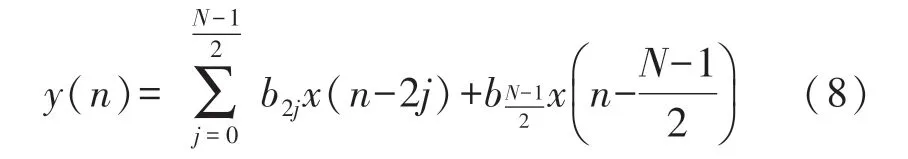
按照差分方程设计的常见的2 倍抽取滤波器的结构如图8 所示。

图8 2 倍抽取N 抽头HB FIR 滤波器结构

信号序列x(n)经过滤波后得到y(n)，再经过2倍抽取后得到序列y(2n)。考虑到对经过计算后的数据进行2 倍抽取，本质上就是每隔一个数据舍弃掉一个数据，若令输出信号序列为y(m)＝y(2n)，此时观察抽取后的差分方程式(9):

式中:x(m)＝x(2n)，代表经过2 倍抽取后的输入信号序列。根据方程可以看出，滤波后抽取可以等效为，对计算前的数据x(n)进行2 倍抽取，因此可以将抽取滤波器的结构再次优化，把抽取环节移动到计算环节之前、移位寄存器环节之后。最终优化后的滤波器结构如图9 所示。

图9 优化后的2 倍抽取N 抽头HB FIR 滤波器结构

但不能将抽取环节再向前移动，因为若在输入时就进行抽取，则差分方程中不会包含一项。而对于N(奇数)抽头的HB FIR 滤波器，存在，使得无法忽略，也即无法在信号序列输入时就进行2 倍抽取。

优化后的抽取滤波器，实际上是在不改变抽取与滤波的差分方程，也即不改变工作原理的基础上，降低了加法器与乘法器的工作频率，可以使滤波器工作在更高的时钟频率下，也因此可以适应更高的输入信号带宽。

以2 倍抽取N抽头的HB FIR 滤波器为例，按照表1 分别设计出每一种滤波器。

表1 滤波器组用到的滤波器

2.2.2 滤波器组设计

对于项目中要求的DDC 的抽取系数，按照表2设计了滤波器的组合方案，滤波器的输入时钟与后续时钟由时钟管理模块产生，clk1、clk2～clk48 为主时钟clk 与其2 至48 分频时钟，所有情况下输入采样率均为fs。

表2 每种抽取模式与滤波器组合

3 电路实现与仿真

3.1 RTL 级设计与仿真

本文使用Verilog HDL 编码实现上述DDC 电路，其中滤波器抽头系数由MATLAB 辅助设计。设计完成后通过ModelSim 对电路进行仿真验证，借助MATLAB 分析输出信号频谱。

最终仿真结果显示，本文设计的基于CORDIC算法的NCO 工作在1 GHz 时钟频率下，输出350 MHz 正弦波时，无杂散动态范围可达110.4 dB，如图10 所示。

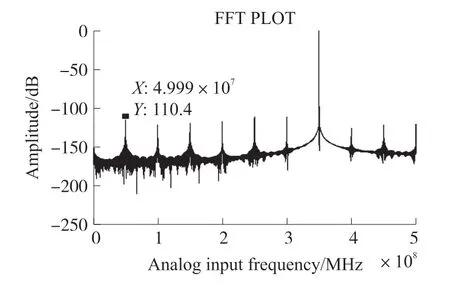
图10 NCO 输出350 MHz 正弦波频谱

整体电路仿真通过输入激励信号为0～500 MHz 的扫描信号，得到DDC 在14 种抽取模式下，输出信号的频谱分别为图11～图24。

图11～图24 显示，所有抽取模式下的DDC 都具有平缓的通带，阻带衰减均大于100 dB，某些模式下即使存在次波峰衰减低于80 dB，但经过抽取后，均折叠到阻带或过渡带，并不影响通带性能，DDC 满足设计需求。各抽取模式的详细参数如表3所示。

表3 每种抽取模式的-3 dB 带宽与阻带衰减

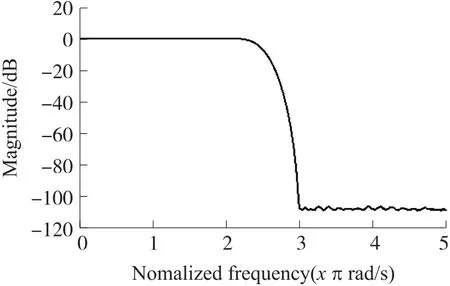
图11 2 倍抽取DDC 频谱图

图12 3 倍抽取DDC 频谱图

图13 4 倍抽取DDC 频谱图

图14 6 倍抽取DDC 频谱图

图15 8 倍抽取DDC 频谱图

图16 10 倍抽取DDC 频谱图

图17 12 倍抽取DDC 频谱图

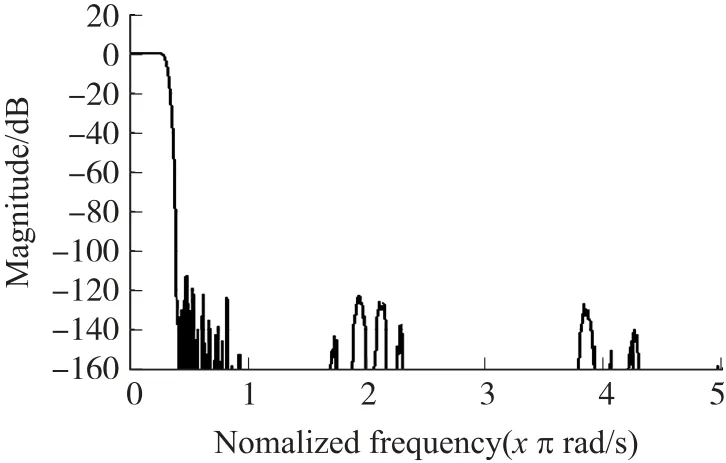
图18 15 倍抽取DDC 频谱图

图19 16 倍抽取DDC 频谱图

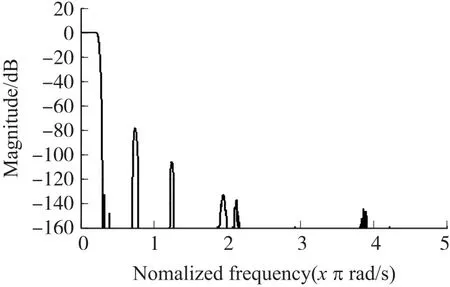
图20 20 倍抽取DDC 频谱图

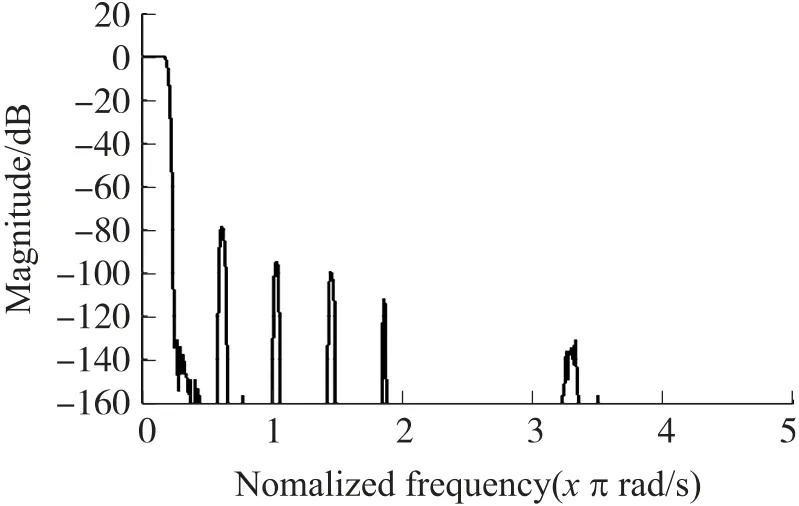
图21 24 倍抽取DDC 频谱图

图22 30 倍抽取DDC 频谱图

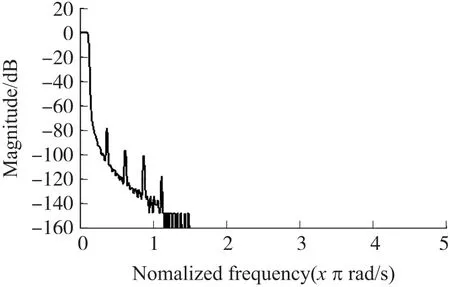
图23 40 倍抽取DDC 频谱图

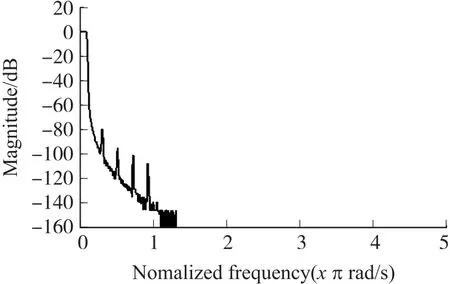
图24 48 倍抽取DDC 频谱图

表4 给出了其他文献与本文中DDC 参数的对比，本文提出的DDC 设计在抽取模式数量、通带带宽和阻带衰减方面均有一定的优势。

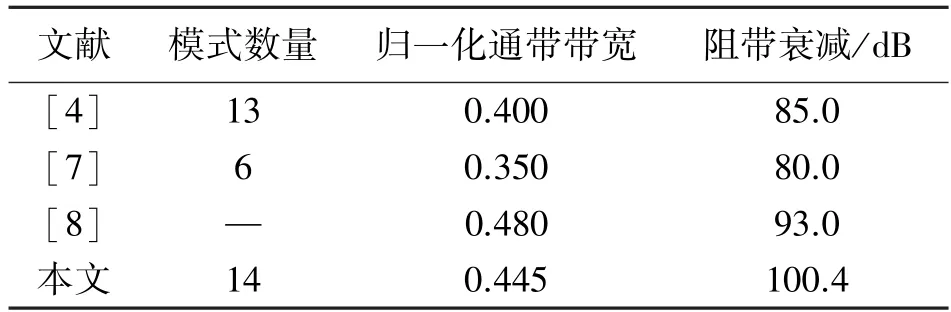
表4 DDC 参数对比

3.2 ASIC 实现与后仿真

本文设计的DDC 与其他数字部分模块一起嵌入1 GS/s 14 bit ADC 进行流片，所有数字部分电路基于28 nm 工艺，使用Synopsys 公司的Design Compiler 和IC Compiler 完成RTL 代码的综合与布局布线。

图25 为DDC 输出波形的前、后仿真结果对比，经过Prime Time 对电路的时序分析，各路径的延时均满足了建立时间与保持时间的要求，后仿结果显示电路功能与前仿一致，该电路满足设计需求。

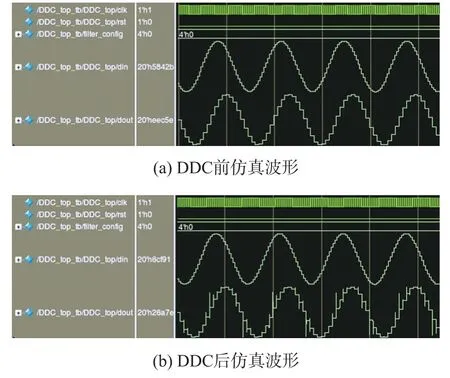
图25 DDC 输出波形的前、后仿真结果

数字部分的IR_DROP 如图26 所示，在设定供电电压0.9 V，翻转率0.8(每周期80%的单元发生翻转)条件下，VDD 的IR_DROP 低于29.86 mV，绝大部分低于8.96 mV；VSS 的IR_DROP 低于26.44 mV，绝大部分低于10.58 mV；均低于满幅电压的3.5%，满足设计要求。

图26 VDD 的IR_DROP 图

最终数字部分版图面积为1 300 μm×1 370 μm(DDC 约占67%)，仿真功耗为301.7 mW。通过STA静态时序分析、IR_DROP 分析、DRC 与LVS 等检查，确定了本设计满足ASIC 设计要求，功能完善。

4 结论

在研究了现有数字下变频电路的基础上，本文提出了一种多模式DDC 电路结构。该DDC 作为一款ADC 芯片的数据处理模块，使用ASIC 设计方法实现。文章改进了传统的抽取滤波器结构，使其具有更高的工作频率，同时提出了一种实现多抽取模式的方法，在28 nm 工艺下完成了版图设计。本设计可以工作在1 GHz 时钟下，对1 GS/s 的14 bit 数据进行下变频与抽取，共可以实现14 种抽取模式，抽取系数包括2、3、4、6、8、10、12、15、16、20、24、30、40、48，最低阻带衰减达到100.4 dB。其中NCO 的无杂散动态范围达到110.4 dB。此外，基于本文提出的多模式DDC，还可以利用时钟门控设计，在不同模式下关闭不工作的滤波器，以减少电路的功耗。本文提出的设计为直接射频采样ADC 中的多模式DDC 电路提供了一种更好的选择。