基于扫描点云数据的零部件边缘轮廓提取技术
王继虎, 樊晶晶,2, 孙安斌, 邹 志
(1.航空工业北京长城计量测试技术研究所,北京 100095; 2.北京航空航天大学,北京 100083)
边缘轮廓线是指两个表面相交形成的一段长度有限的直线或曲线。零件的边缘轮廓线一定程度上定义了零件的空间范围和几何尺寸。边缘轮廓线的空间约束属性和尺寸定义属性使其成为产品质量检测的重要对象。
边缘轮廓的加工精度是保证零件装配质量的重要因素。对于大型零件,其边缘轮廓的加工偏差决定了装配质量和效率,如飞机风挡玻璃、蒙皮、雷达罩等大型薄壁零部件。飞机大部件具有尺寸大、刚性低、价格昂贵的特点,为使其充分发挥预期作用,应保持其处于良好的装配状态。受加工工艺的影响,飞机大型零部件的边缘轮廓与理论边缘轮廓存在不同程度的偏差,使得装配后的零部件和装配框体或桁架之间存在应力,或装配间隙不符合要求,影响零部件的使用寿命和整机的安全性和气动性能。因此,为保证大型零部件的装配质量,提高装配效率,零件的边缘轮廓线需要进行在线或线下检测及评价。同时,在三维模型数字化分析领域,如逆向工程及飞行器隐身性能分析[1]方面,零件边缘轮廓检测也是重要的研究内容。
综上所述,零件边缘轮廓线的识别提取技术在产品质量检测、装配和数字模型分析等方面具有重要的作用。现有的零件边缘轮廓识别方法可分为基于二维图像的检测[2-3]和基于三维点云数据的特征点识别[4-5]两类。图像检测方法因为不能反映三维零件完整信息具有一定局限性。现有的基于点云数据的识别方法具有计算量大的、参数取值自适应性差的特点。为提高边缘轮廓数据的识别效率和准确度,本文提出一种基于点云数据的边缘轮廓提取方法。
1 边缘轮廓线分类及定义
从边缘轮廓线的形成方式出发,通过构造切片提取包含边缘轮廓数据点的截面线数据,然后基于相邻点法向夹角分布规律,提出采用模式向量表征截面线特征的方法。根据两相交面型的不同,边缘轮廓线分为平面-平面相交型、平面-球面相交型、球面-球面相交型、平面-自由曲面相交型、球面-自由曲面相交型。
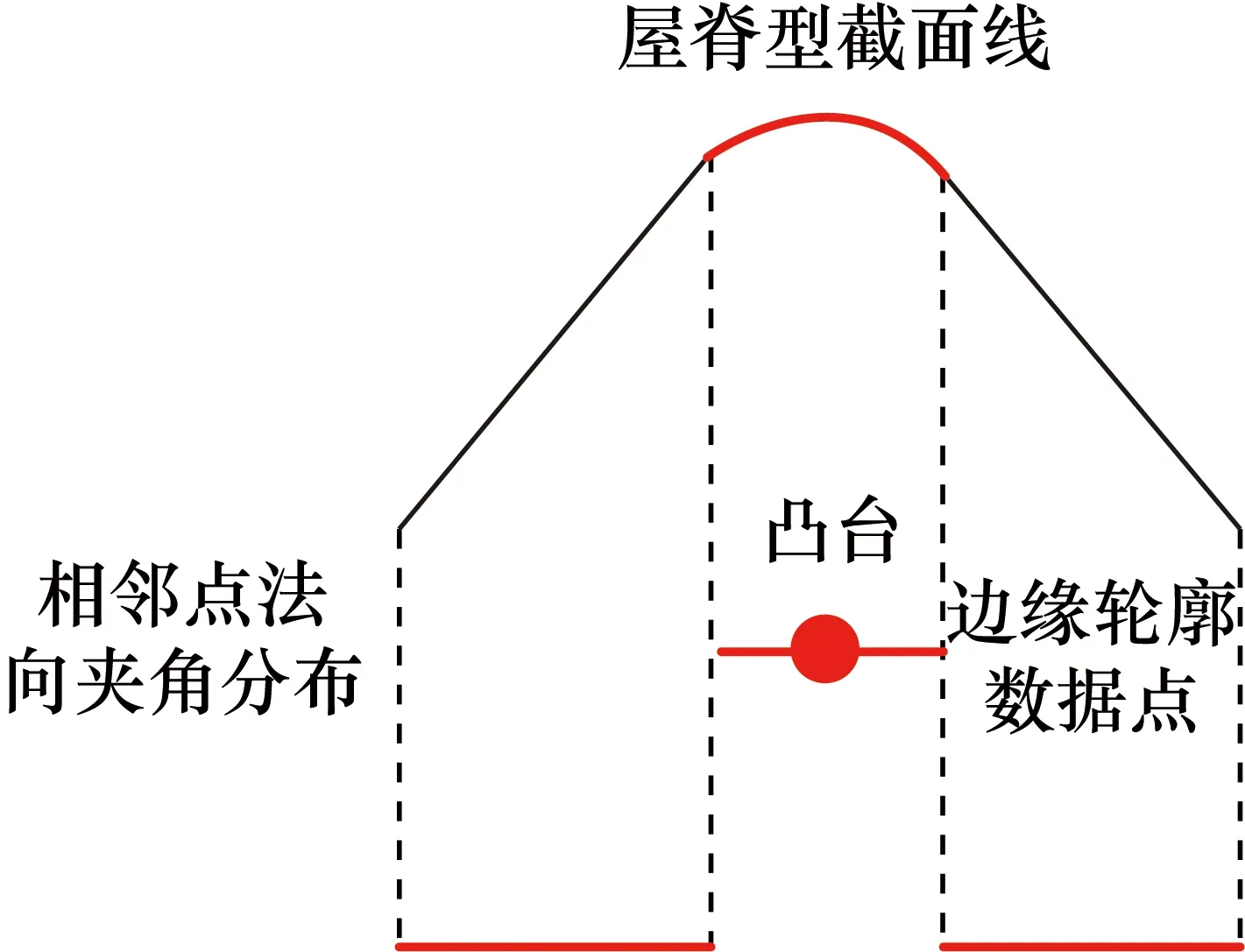
根据相交是否存在过渡圆弧,将截面线又分为屋脊型和折线型,其中屋脊型是指存在过渡圆弧的情况,折线型是指不存在过渡圆弧的情况。图1(a)显示了两种相交类型及截面线上的边缘轮数据点(红色点)。图1(b)显示了5种面型相交类型的边缘轮廓线的截面线。5种截面线的相邻点法向夹角分布如图1(c)所示。从相邻点法向夹角分布可知,每种截面线均存在曲率恒定的一端,且从曲率恒定端开始,第一个曲率变化的点为边缘轮廓线上的点(红色点)。

图1 5种边缘轮廓线的截面线分布及截面线的法向夹角分布
基于相邻点的法向夹角定义模式向量表征了截面线上边缘轮廓数据点邻近区域的曲率变化特征。模式向量表示为[A,A,A,B,…,B,C,C,C]。其中,[A,A,A]和[C,C,C]表示截面线上两相交面型对应的相邻点的法向夹角取值;[B,…,B]表示截面线上过渡圆弧区域的相邻点法向夹角取值,B的个数n与过渡圆弧弧长S的关系为
(1)
式中,d为扫描点云数据的平均距离。
当两面型直接相交时,模式向量中仅包含一个B,且该B的取值为两相交面型在相交处的切平面的夹角。A,B,C这3个元素不同的取值,对应于图1(c)中截面线法向夹角分布线上不同的台阶高度。
2 基于点云数据的边缘轮廓提取过程
以平面-平面型边缘轮廓线的提取为研究对象。针对折线型和屋脊型截面线数据分别采用拟合求交法和重心计算法提取边缘轮廓数据点。
2.1 截面线数据的获取
原始的扫描点云数据由大量离散点构成,不具备拓扑结构信息[6]。首先将原始点云数据在GOM Inspect软件中进行网格化[7],使离散的点云数据变成由三角形连接的连续整体。
提取截面线数据可分为两步:首先在待提取的边缘轮廓线附近手动点选多点拟合一条样条曲线作为初始轮廓线;然后沿初始轮廓线的法向构造等间隔的万向切片,并计算万向切片与网格化点云数据的交点,则每个切片与网格点云数据的交点构成一组截面线数据。图2展示了提取截面线数据的过程,万向切片为定半径的圆平面,提取的截面线数据为多组离散的数据点,如图2中红点所示。
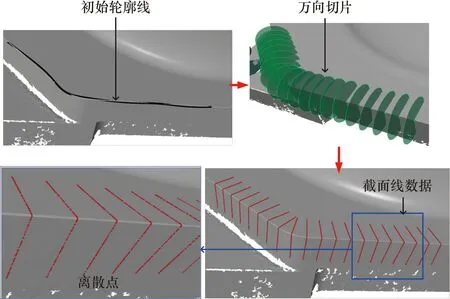
图2 截面线数据提取过程
2.2 模式向量识别截面线类型
平面-平面型边缘轮廓线的截面线数据呈直线-直线相交形式。屋脊型和折线型截面线的离散数据点分布规律不同,因此需要采用不同的方法识别。
识别截面线数据类型的过程可分为法向夹角序列计算和基于跳变元素个数的类型判别。具体计算过程如下。
(1) 计算法向夹角序列。
现有扫描设备获得的点云数据,通常包含坐标和法向信息。若不包含法向信息,则可通过局部平面拟合法[8]、主成分分析法、邻域加权平均法[9]等方法获得。
① 通过向量内积的方式获得相邻点的法向夹角,设一组截面线数据的法向夹角序列为(α1,α2,…,αm-1),其中m表示该组截面线数据包含的离散点个数。
③ 从最后一个元素开始,逆序对法向夹角序列进行步骤②的判断,获得法向夹角序列停止跳变的位置,设为j。
(2) 类型划分准则。
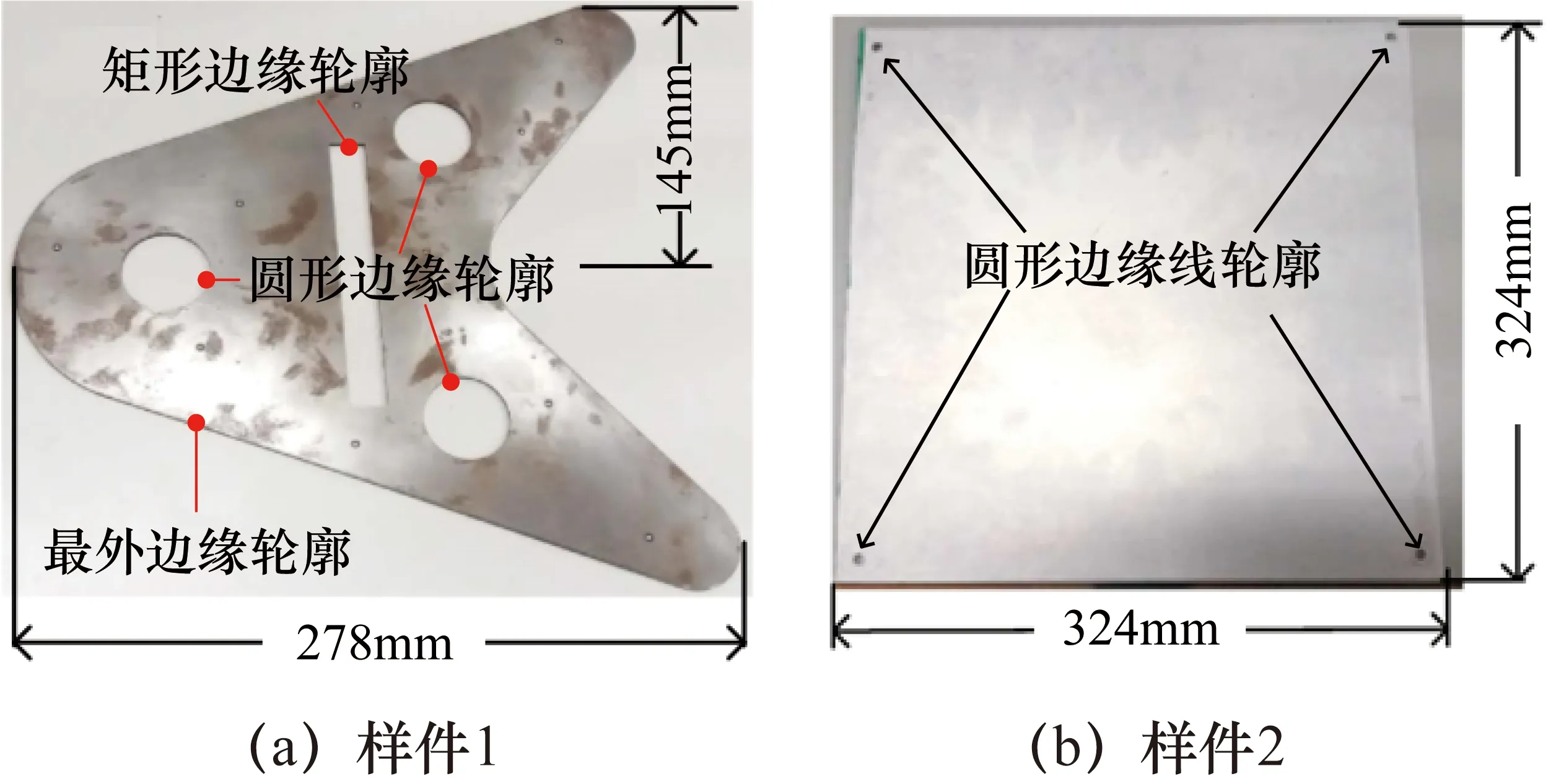
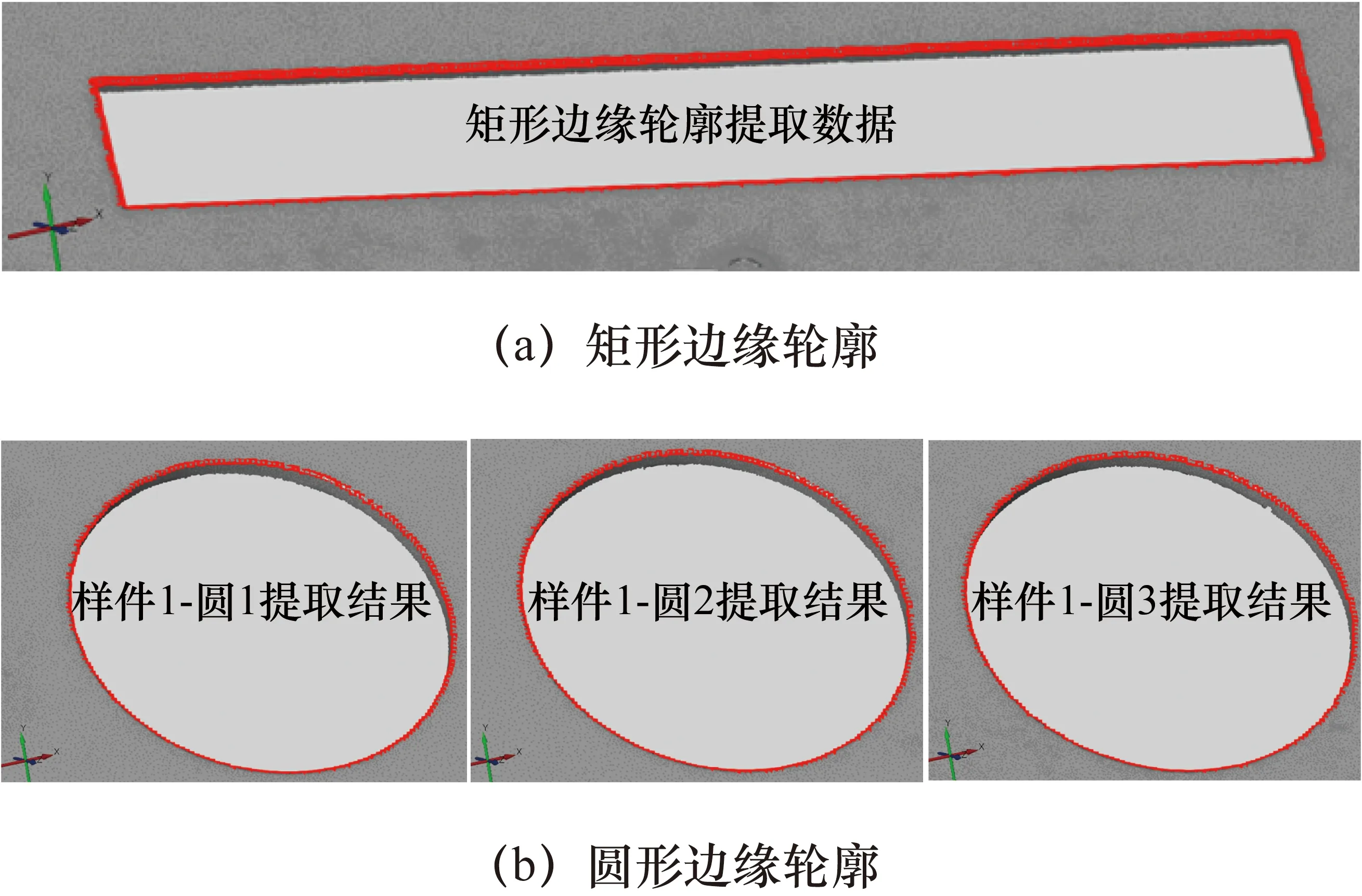
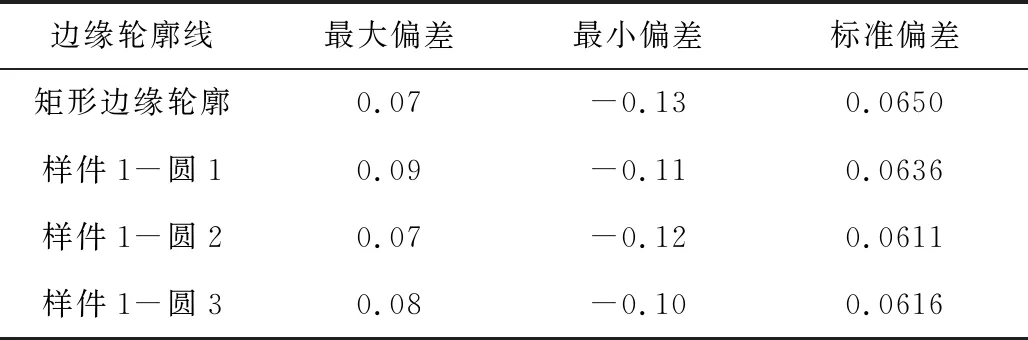
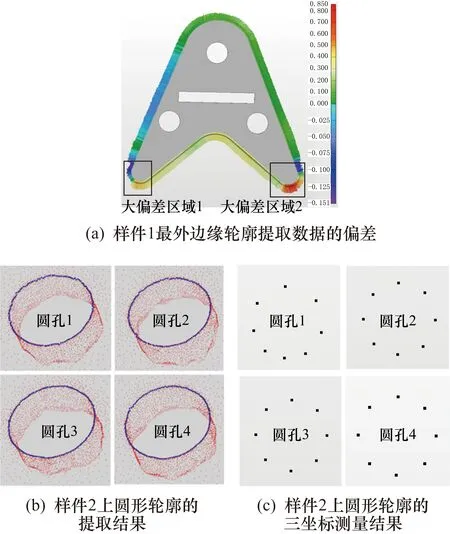
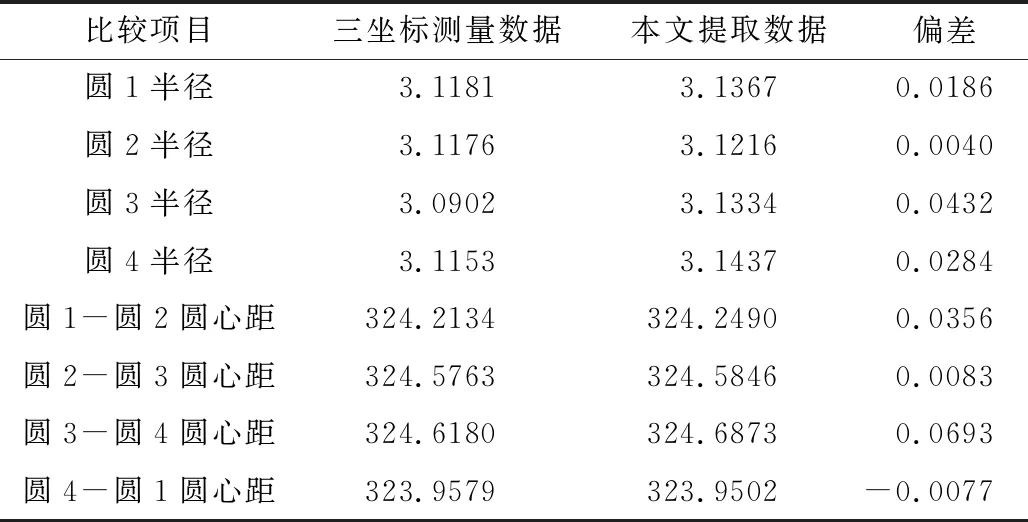
计算一组截面线数据法向夹角序列包含的跳变元素个数,即j-i-2个。当1≤j-i-2 识别出截面线类型后,分别采用拟合求交法和重心计算法提取折线型和屋脊型截面线的边缘轮廓线数据点。两种方法的计算过程如下。 2.3.1 拟合求交法 对于折线型截面线,其两端的数据呈直线分布,且两条直线的交点即为边缘轮廓线数据点。因此采用直线拟合求交的方式获得目标点。具体计算步骤为:首先对截面线数据进行降维处理,即将截面线数据投影到二维平面;然后在二维平面上用截面线两端的数据点拟合两条直线,并计算两条直线的交点;最后将交点转换到全局坐标系下得到全局坐标系下的边缘轮廓数据点。 (1) 截面线数据的降维处理。 (2) 式中,D(P1,Pi)表示两点的空间距离。 (2) 拟合两条直线求交点。 通用的二维直线表达式为y=ax+b,则最小二乘拟合求解(a,b)的过程为 (3) 式中,(xs,ys)为截面线数据在二维平面坐标系下的坐标。起始端2/5数据点拟合直线时,式(3)中的g=1,h=[2/5×m]。结束端2/5数据点拟合直线时,式(3)中的g=n-[2/5×m],h=m。 (4) (3) 将交点转换到全局坐标系下。 将平面法向作为Z轴正方向,与平面坐标系的X轴和Y轴构建一个局部三维坐标系。根据全局三维坐标系和局部三维坐标系坐标轴的对应关系,求解两个坐标系的旋转矩阵R和平移向量T。设局部坐标系的X轴、Y轴、Z轴的单位向量分别表示为(n′xi,n′xj,n′xk),(n′yi,n′yj,n′yk),(n′zi,n′zj,n′zk),则旋转矩阵R的计算过程为 (5) (6) 2.3.2 重心计算法 屋脊型截面线的相邻点法向夹角呈台阶状分布,如图3中红色线段所示,台阶上升沿和下降沿之间的区域对应截面线上的过渡圆弧区域。根据对称性,将台阶的中点位置作为边缘轮廓点的位置(如图3中红色点所示)。 图3 屋脊型截面线上相邻点的法向夹角分布 实际测量时,过渡圆弧表面的法向发生变化使投射到该处的测量光在经表面反射到光电感应器上所成的像发生畸变,进而影响测量结果的准确度[10],导致该处相邻点的法向夹角分布与凸台阶状存在一定程度的偏差。 为减小法向夹角分布偏差对提取结果的影响,采用重心法识别屋脊型截面线上的边缘轮廓点。重心法是指通过重心计算表达式求解边缘轮廓点的过程。通过重心计算表达式可求出αr在dr维度上的重心,计算公式为 (7) 式中,dr为截面线数据中第r个离散点相对于第1点的折线距离,且d1=0;αr为第r个离散点与第r-1点的法向夹角,且α1=0。 重心法提取屋脊型截面线边缘轮廓点时,首先计算截面线数据的相邻点法向夹角序列和相邻点之间的欧氏距离;然后计算离散点的折线距离,表示为序列{d1,d2,…,dm};最后根据重心计算表达式计算截面线数据的重心位置G。根据G的取值确定其在折线距离序列{d1,d2,…,dm}中的位置q,使该位置满足dq≤G≤dq+1(q≤m-1),则将截面线上第q点和第q+1点的插值点作为边缘轮廓点。每点的折线距离是其前面各相邻点欧式距离之和。第r点的折线距离dr(1 (8) 为验证本文所述方法的有效性和准确度,对两类边缘轮廓线进行试验验证。试验用样件如图4所示。样件1上的最外边缘轮廓线存在2 mm的过渡圆弧半径,且圆弧长度为1.57 mm,属于屋脊型边缘轮廓线,其上的矩形和圆形边缘轮廓线为折线型。样件2上的4个圆柱孔与上表面相交形成的圆形边缘轮廓线属于屋脊型,圆弧长度为0.314 mm。 图4 试验样件及试验用边缘轮廓线 采用结构光扫描仪ATOSⅡ对3个样件进行扫描,获得包含边缘轮廓线数据的离散点云数据。结构光扫描仪ATOSⅡTriple Scan的探测误差[11]为0.006 mm,球空间误差[11]为0.005 mm。两个样件的离散点云数据分布如图5所示。 图5 试验样件的扫描数据 为评价两种方法的准确度,将提取的边缘轮廓点与理论边缘轮廓和三坐标机测量数据进行比较。 分别采用拟合求交法和重心计算法提取样件1和样件2上的边缘轮廓线数据。试验中,本文设置的切片间距为1 mm。对于折线型边缘,切片半径为3 mm;对于屋脊型边缘,切片半径为4 mm。边缘轮廓数据点的识别结果如下。 (1) 折线型边缘轮廓识别结果。 折线型边缘轮廓的提取结果如图6所示,提取的边缘轮廓点用红色离散点表示。 图6 折线型边缘轮廓数据点的提取 在GOM Inspect软件中,对提取的圆形边缘轮廓数据和矩形边缘轮廓数据进行已知尺寸的圆拟合(标称半径18 mm)和矩形拟合(标称尺寸128 mm×16 mm)。提取的边缘轮廓点相对于标称尺寸轮廓的偏差统计结果如表1所示。 表1 折线型边缘轮廓线提取数据点的的偏差 单位:mm 从表1可知,4条折线型边缘轮廓提取数据相对于标称尺寸轮廓的最大偏差在0.1 mm以内,最小偏差在-0.15 mm以内。4条轮廓线的标准偏差均在0.07 mm以内。所以,所述的拟合求交法的单点提取准确度在-0.15~0.1 mm范围内。 (2) 屋脊型边缘轮廓识别结果。 将样件1最外边缘轮廓的提取结果与理论设计线在PolyWorks软件平台进行匹配[12]并比较,比较结果如图7(a)所示,偏差在-0.151~0.860 mm范围内。因为实物样件1在偏差较大区域存在肉眼可见的加工误差,所以提取数据偏差较大(见图中标注的大偏差区域)。除该区域外,该边缘轮廓其他位置处的偏差在±0.2 mm以内。实验样件2上4个圆形边缘轮廓的提取结果如图7(b)所示,每个圆形边缘轮廓共144个点。三坐标机的测量数据如图7(c)所示,每个圆形边缘轮廓共有8个点。将提取的圆形边缘轮廓点分别进行最小二乘圆拟合,并与三坐标机测量数据的拟合结果进行比较,比较结果如表2所示。 图7 屋脊型边缘轮廓数据点的提取 表2 样件2上4个圆形边缘轮廓提取数据的偏差 单位:mm 从表2可知,样件2上4个圆形边缘轮廓提取数据的拟合半径相对于三坐标测量数据拟合结果的偏差在0.05 mm以内,圆心距偏差在0.07 mm以内。 综上所述,所述的重心计算法的单点提取准确度在±0.2 mm以内,提取结果的形状拟合准确度在0.07 mm以内。 针对大型零部件边缘轮廓检测效率低的问题,本文提出一种基于扫描点云数据的零部件边缘轮廓提取技术。该技术基于相邻点法向夹角分布定义了模式向量用以表征折线型和屋脊型直线与直线相交截面线的分布规律。该提取技术首先构造万向切片提取包含边缘轮廓线数据点的截面线数据;然后通过识别截面线数据的模式向量确定其类型;最后根据截面线的类型分别采用拟合求交法和重心计算法识别其上的边缘轮廓数据点。本文对多条边缘轮廓进行提取试验,并将试验结果与参考量进行比较。结果表明:拟合求交法的单点提取准确度在以-0.15~0.1 mm以内,重心计算法的单点提取准确度在±0.2 mm以内,提取结果的形状拟合准确度在0.07 mm以内。 所述方法适用于零部件上平面-平面相交型边缘轮廓的提取,有利于大型零部件边缘轮廓非接触、数字化检测技术的形成。所述方法的准确度与扫描点云数据的质量和点间距等因素密切相关。当点云数据质量较差时,需要在处理过程中增加必要的光顺去噪等步骤。2.3 边缘轮廓数据点的提取方法
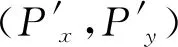
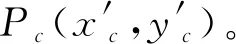
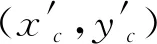
3 验证实验
3.1 实验样件

3.2 实验结果
4 结束语

