基于粒子群优化算法的蒸汽热网改造研究与验证

金康华，王叶飞，孙海龙，林小杰，蔡东平，李 岚，钟 崴

(1.浙江浙能绍兴滨海热电有限责任公司 技术部，浙江 绍兴 312000；2．浙江大学 能源工程学院，浙江 杭州 310000;3.常州英集动力科技有限公司 工业部，江苏 常州 213000)

0 引言

随着我国工业化进程的不断深入，集群式的工业园区因其资源集成、联动发展、环境友好的优势[1]，已成为拉动区域经济增长、推动区域技术创新的新动能与推进我国城镇化建设的有效途径。而工业园区并非静态建设规划一次成型，其产业规模的不断扩张、产业结构的不断重组给工业园区能源系统尤其是供热系统的动态设计带来了挑战。同时，《能源发展“十三五”规划》也指出：建设清洁低碳、安全高效的现代能源体系。面向需求与政策双重导向，如何运用新建管网智能规划解决供热系统增量扩容和热网结构日趋复杂条件下的局部管路过载、供需不匹配的问题，需要智慧供热理念在以集中供热为主要供热方式的工业园区[2]中深入运用，即以基于模型的供热规划为技术核心，以基于智能优化算法的机器解算为技术支撑，推进供热系统规划的智能化、精细化发展。

针对工业园区复杂蒸汽供热管网突出的安全性与品质保障问题，传统的供热系统大多依靠经验对管网流量输配进行调节[3]，能源浪费现象严重。因此，国内外学者着眼于工业园区蒸汽供热系统的模型构建、优化改造等方面的研究。

在建模方面，孙玉宝[4]在蒸汽管网计算模型中，结合节点方程法对水力和热力计算进行联合求解，结果显示这一方法获得的节点压力和节点温度的相对误差大部分在5%以内，满足工程精度要求；李晓红等[5]以瞬变流理论与特征线求解方法为基础，建立了可反映蒸汽管网运行波动的瞬变数学模型；涂惟民等[6]通过分析枝状布置蒸汽管网的特点，建立了一种针对枝状蒸汽管网优化的多主轴分级计算方法。

在工业园区蒸汽输配网络规划设计方面，张全斌等[7]对蒸汽管道输送距离影响因素做出了分析，为长距离供热的规划设计提供了指导；白子强[8]以蒸汽管网安全、经济运行为目标，提出了有效的管网优化方法；杨丽芳[9]借助DSZ-PROSS软件模拟分析，通过工业母管和原有管道跨接的方式，解决了原有蒸汽管线压力不匹配及局部管段存在的压阻瓶颈的问题。

然而，尚未见考虑蒸汽热网动态发展，基于机理模型寻优的热网规划改造策略研究。因此，本文建立了工业园区蒸汽热网机理模型并基于历史运行数据校验模型，采用粒子群优化算法求解以提高末端供汽品质作为目标的优化问题，得到管网最优改造策略，并以预测性手段分析拓扑结构变动对蒸汽流量输配的影响，实现对蒸汽系统供汽品质的改善。

1 蒸汽热网建模及优化改造方法

本文通过建立与实际热网系统相对应的仿真模型及两者的实时双向映射关系，以较为经济的预测性手段分析拓扑结构变动对蒸汽流量输配的影响，从而求解优化问题得到可以用于实际生产生活的蒸汽热网拓扑结构最优改造策略，实现对蒸汽系统供汽品质的高效改善。

1.1 工业园区蒸汽热网机理仿真模型

本文基于工程热力学、传热学及流体力学相关机理方程和实际管网结构(如图1)建立工业园区热网模型。为简化计算，本文采用基于图论的方法，将供热管网中管道部件定义为“区段”，将除管道外的其他部件(如阀门等)定义为“节点”，并通过节点关联矩阵有效连接。热网模型经迭代计算求解后可得出全网蒸汽温度、流量、压力等参数的分布，以支撑后续的数据验证及改造方案寻优。

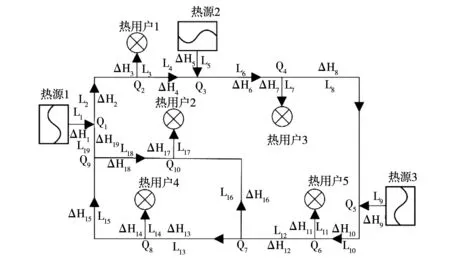
图1 工业园区蒸汽管网的结构示意图

针对含有a个节点、b条管段、c个闭环回路的蒸汽管网，由基尔霍夫第一定律建立节点处的流量守恒方程

AL=Q

式中A(a×b)——节点区段关联矩阵；

L——各个区段内的流量向量，L=[L1,L2,…,Lb]T；

Q——各节点净质量流量的向量，Q=[Q1,Q2,…,Qa]T，一般取流入该节点为正值，流出该节点为负值。

由基尔霍夫第二定律可知，在闭合回路中的压降和温降等于零

BΔH=0

BΔT=0

式中B——闭合回路关联矩阵；

ΔH——闭合回路的管段压降矩阵,ΔH=[ΔH1,ΔH2,…,ΔHb]T；

ΔT——闭合回路的温度降矩阵ΔT=[ΔT1,ΔT2,…,ΔTb]T。

由流体力学相关方程可求得管线段的压力降

ΔH=ε|L|L+ΔZ-P

式中P——闭合回路中管网水泵的压力降矩阵，不存在水泵时，取P=0；

ε——管线段的压力修正系数；

ΔZ——管线段地理标高最大值与最小值的差值。

管线段的温降与该管线段的焓降和散热量有关，焓降的计算式为

式中hin、hout——管段进、出口焓值/kJ·kg-1；

Vin、Vout——管段进、出口流速/m·s-1；

Qj——管线段的热损失/kJ；

q——管线段的质量流量/kg。

单位长度管线段的热损失Qi计算式为

Ql=KπDo(Tm-Ta)

式中Do——管线段的外径/m；

K——换热系数/kJ·(kg·m·℃)-1；

Tm、Ta——蒸汽温度/℃、环境温度/℃。

其中管线外径Do和换热系数K的计算式如下

Do=Dm2δp+2δisu1+2δisu2

式中Dm、δp——管道内径/m、管壁厚度/m；

δisu1、δisu2——内、外层保温层厚度/m；

λp、λisu2、λisu2——管道管壁、内层保温层、外层保温层导热系数/kJ·(kg·℃)-1；

hm、ho、hr——蒸汽和管壁的对流换热表面传热系数、管道外保温层和外界环境的对流换热表面传热系数、管道外保温层与外界环境的辐射传热系数/kJ·(kg·m·℃)-1。

通过联立上述水力平衡及热力平衡方程，即可求解多热源联合供热的闭合式蒸汽热网模型。考虑模型在工程实际应用的可行性，本文提出根据实测数据和仿真结果进行误差分析，计算单个用户的温度、压力的相对误差，并以单个参数相对误差的加权平均值表征整网的相对计算误差，如果单个参数误差与整网平均误差均小于5%，即可认为该仿真模型符合计算精度要求，具有良好的工程应用价值。

1.2 工业园区蒸汽热网优化改造方法

为评价在不同改造方案对整网参数变化的影响，以代表性用户在改造前后的温度压力作为评判标准，本文设定优化系数η作为优化函数目标

式中Pia、Pib——联通管段联通前后特征用户i的计算压力/MPa；

Tia、Tib——联通管段连同前后特征用户i的计算温度/℃；

n——代表性热用户数量。

在实践中，优化变量为具体改造方案，优化变量通过所研发的模型得出全网各处参数后进一步算出优化函数值(即前文所述的优化系数)，对应的，优化过程中所涉及的约束主要由地形和项目现状等决定。因为工业蒸汽管网结构复杂，改造优化方案多样，对优化算法的收敛性和稳定性及收敛速度均有较高要求，故而本文提出采用智能优化算法中的粒子群算法来对上述问题进行优化求解。

粒子群优化算法是一种典型的群体智能优化算法，它的思想源于对鸟群简化社会模型的研究及行为模拟[10]。它将模型中的个体抽象为没有质量和体积的粒子，而粒子所处位置表示解空间中可能解的位置，通过个体间的信息传递，导引粒子群体按一定规律向可能解的方向运动从而寻找到最优解。本文的目标是为了在不抬高源侧供汽压力和保证管网安全稳定运行的前提下寻找可以提高管网整体供汽性能的最优改造方案，这一优化问题可表述为如下的具体粒子群优化算法：

将优化变量(具体改造方案)组合为d维粒子，从而把优化问题转化为d维空间中粒子群运动问题。在本文中，单个粒子可理解为一组蒸汽管道优化改造方案，其最优解则是热网末端代表性用户用汽压力的最优改善比例。各粒子在运动过程中，算法通过对个体最优和全局最优粒子的学习进行搜索并逐步找到最优解。具体而言，在生成初始位置后，第i个粒子的位置可表示为Xi=[xi,1,xi,2,…,xi,d]，速度可表示为Vi=[vi,1,vi,2…,vi,d]，每一次迭代，粒子根据如下公式更新位置

Vi(t+1)=wVi(t)+c1r1[pbesti-Xi(t)]+

c2r2[gbesti-Xi(t)]

Xi(t+1)=Xi(t)+Vi(t+1)

式中c1、c2——加速度系数；

r1、r2——0～1范围内的随机数；

pbesti、gbesti——粒子个体最优值向量、全局最优值向量；

w——惯性权重系数，本文采用线性递减的惯性权重来提高算法的收敛性。

式中Itemax、Ite——最大迭代次数、当前迭代次数；

wmax、wmin——惯性权重的最大值1、惯性权重的最小值0。

上述具体实现的计算流程如图2所示。

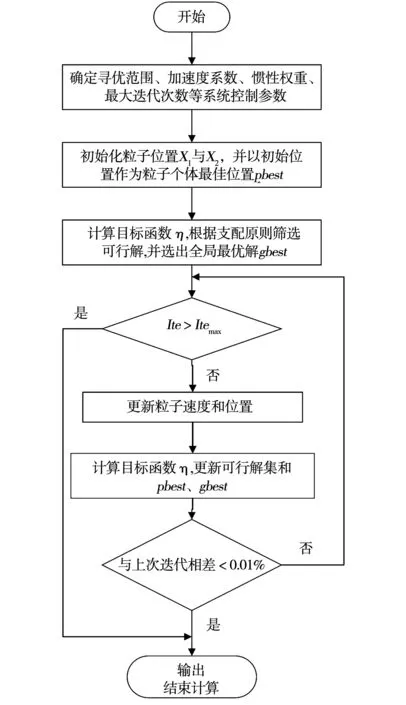
图2 单目标粒子群算法流程图

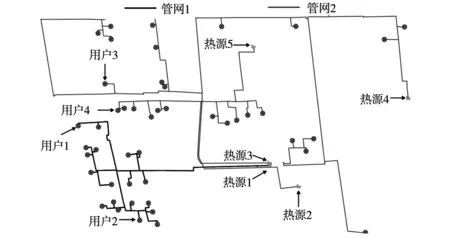
图3 低压管线结构图

2 案例实践与结果分析

2.1 案例介绍

本文所探讨案例为浙江绍兴某热电公司运营的蒸汽热网。该供热系统目前采用多热源联合供热，热源分散在4个区域，为周边企业供应蒸汽。由于系统规模增大，支线数目增加，热用户数量用量分布不一，导致目前蒸汽管网运行期间间歇性出现部分管网负载过高，用汽压力较低的现象。图3为该热网中由管网1和管网2组成的低压管线结构图，并对有代表性的末端用户进行了标注。某典型工况下，管网1的流量Q1=338.52 t/h，温度T1=263.2 ℃，管网2的流量Q2=402.47 t/h，温度T2=252.1 ℃。如果增大管网1的供汽量，会迅速导致末端部分用户的压力在使用过程中低于合同值的Pd=0.5 MPa，从而影响园区内用户的用汽品质，这一现象客观上制约了管网1区域新增热负荷的潜力。

历史运行数据显示，管网2的末端用户的压力参数略高于管网1的末端用户的压力参数，因此可考虑引入旁通管线，优化各条管线压力分布，从而实现供汽性能的优化，实际中的困难在于如何确定这一联通管线的优化布局。

2.2 蒸汽热网优化改造分析

在前述仿真模型的支撑下，本文针对案例中蒸汽热网所存在的问题建立管网1和管网2相应的热网机理模型，并通过典型工况的计算，得出代表性用户处的蒸汽参数仿真结果，与实测数据进行对比，如表1所示。随后，基于实测数据对该案例模型进行误差分析，如图4所示。

从图4计算结果可知，代表性用户处的单个参数的误差均小于5%，符合工程计算精度要求，该模型能真实的反映管网特性，具备进行预测性分析与支撑改造决策的能力。

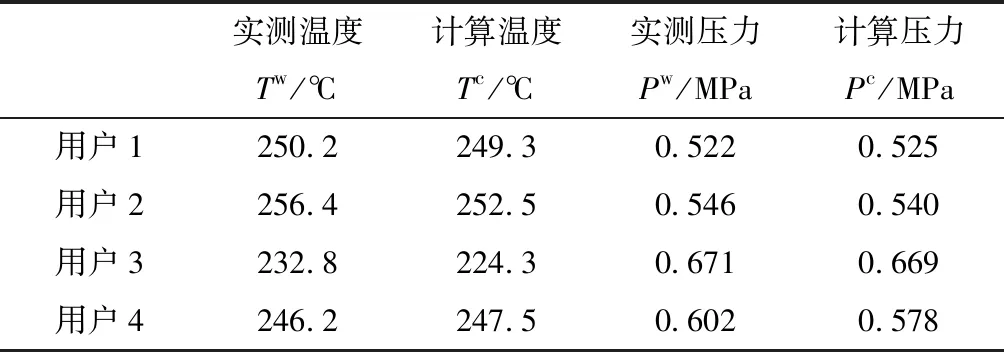
表1 代表性用户的仿真计算结果

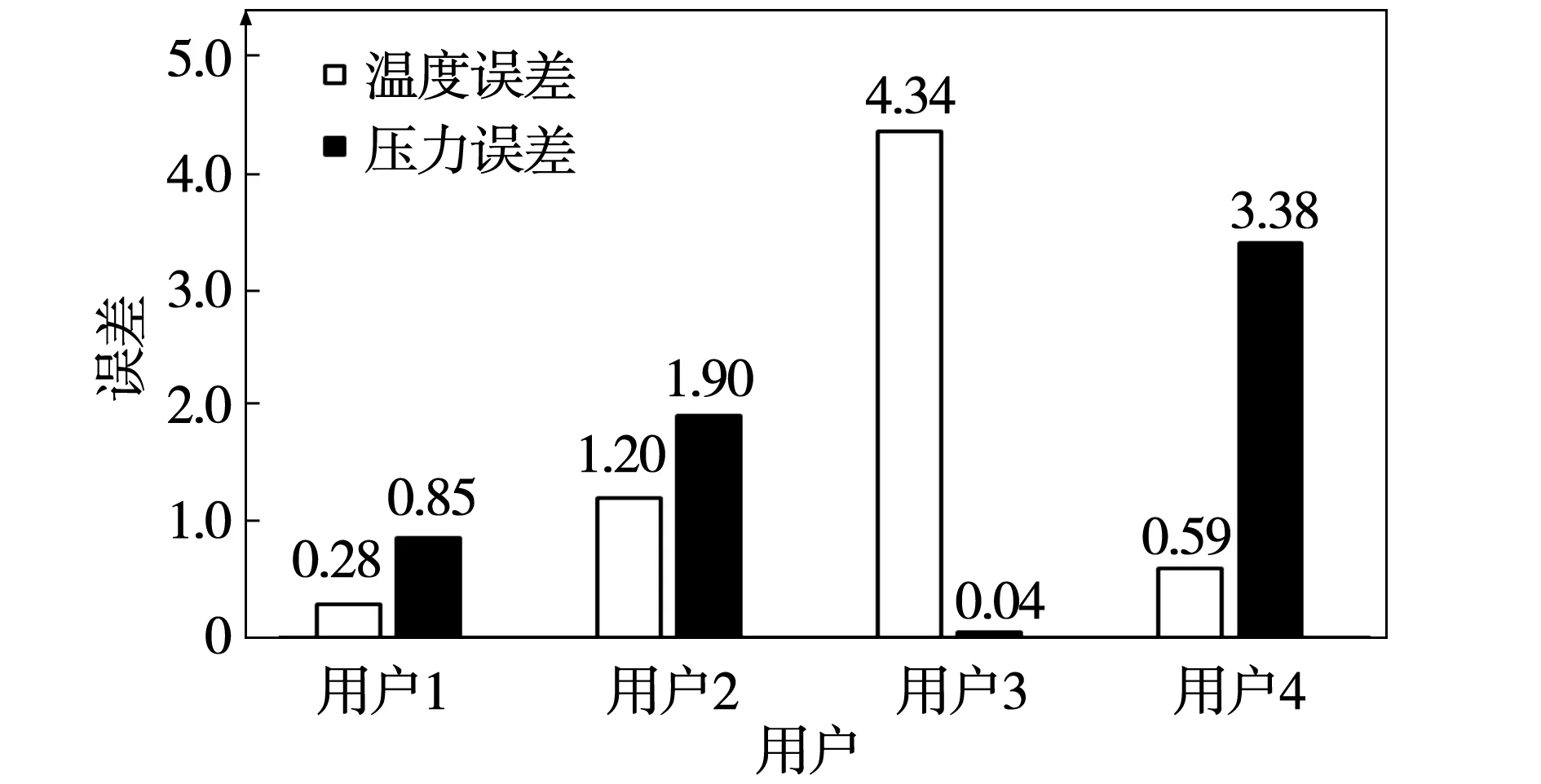
图4 代表性用户仿真计算误差分析结果

前期调研后，考虑到现场施工约束，新建的DN400联通管段只能铺设于管道1和管道2之间。管道1和管道2的具体位置如图5所示。

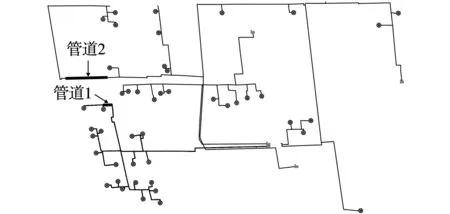
图5 管道1与管道2的位置示意图

在本案例中将管道1与管道2上的联通点相对于图4中对应管道左端的长度分别记为X1和X2，并引入至粒子群算法中作为坐标，则管道1和管道2的联通点相对位置的计算式为

Y=kX+b

管线1和管线2联通点相对位置方程中具体系数与约束范围如表2所示。

表2 管线1与管线2的相对位置方程系数取值范围

同时，联通管段的长度l可由下列方程组求解

式中XL1、YL1——联通管段位于管线1上的连接位置的坐标/m；

XL2、YL2——联通管段位于管线2上的连接位置的坐标/m；

系数0.705、系数0.665——管线1与管线2与水平夹角的余弦函数值；

l——联通管线长度/m。

以X1和X2作为自变量，采用图2中的粒子群算法，设置粒子数为100个，这一寻优过程中优化系数η随X1和X2的不同取值的变化如图6所示。最后，当X1=20.72 m，X2=659.32 m时，获得最优解，此时优化系数η=39.17%，联通管线长度l=429.28 m。

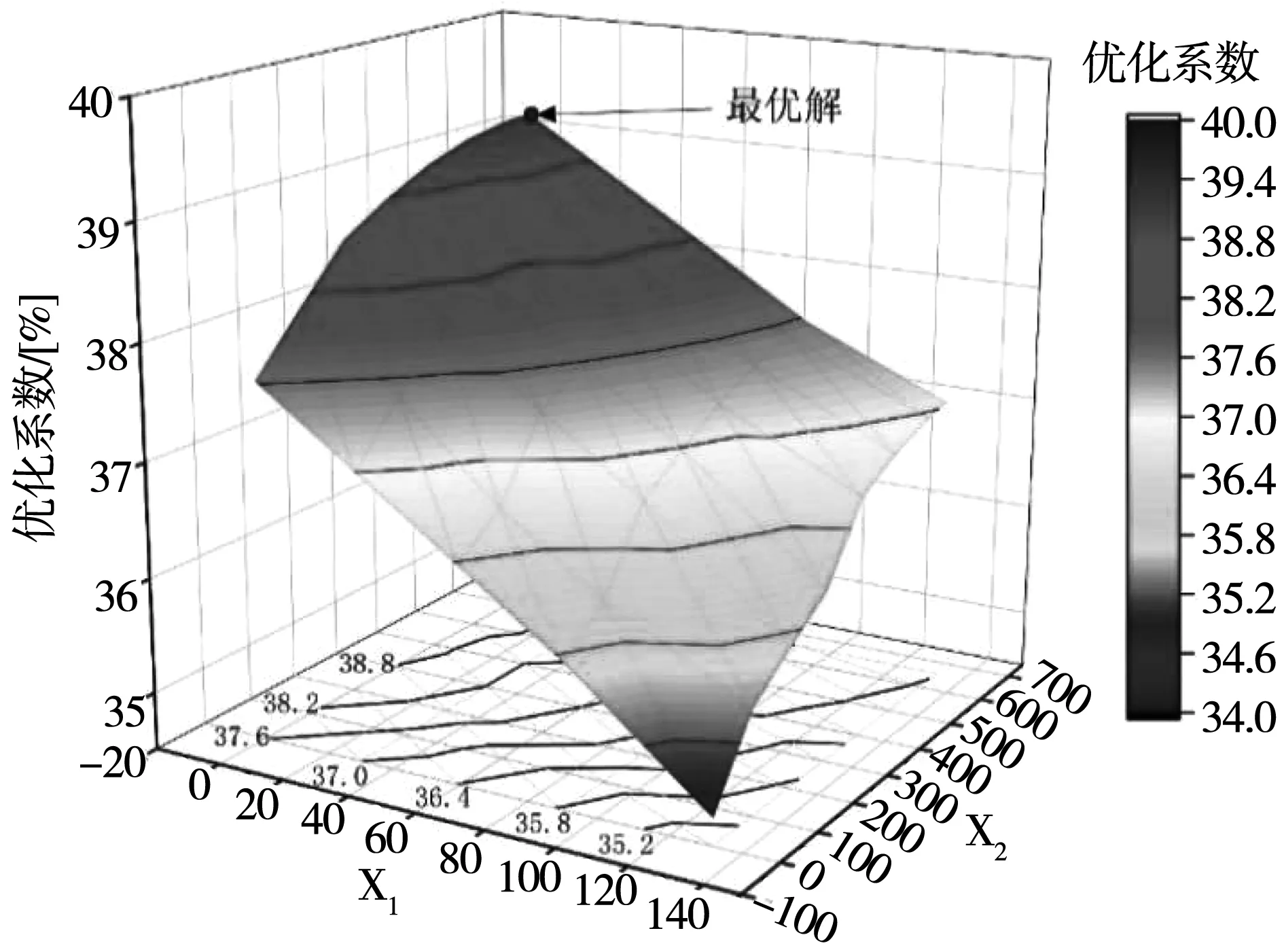
图6 优化系数随X1和X2的不同取值的变化

2.3 改造方案验证

2.3.1 改造方案仿真验证

为了验证这一联通管安装思路的合理性，本文再次建立管网1和管网2联通后的模型。这一模型中，新建联通管段如图7所示，通过对该模型进行仿真计算，代表性用户的蒸汽参数在两个供热管网末端联通前后的计算结果如表3所示。

由表3计算结果可知，两个管网末端联通后，压力较高的管网2的用户，如代表性用户3和用户4的实测压力几乎不变；而压力较低的管网1的用户，如代表性用户1和用户2的实测压力抬升ΔP=0.1 MPa；同时，不同于其他代表性用户在联通后温度的略有上升，用户1的温度随着管网的联通会发生明显的降低，降低值ΔT=10 ℃。仿真计算结果表明，联通管网1和管网2的末端来抬升管网1的末端用户的压力的决策是可行的，但是用户1的温度可能降低，从而影响其蒸汽品质。

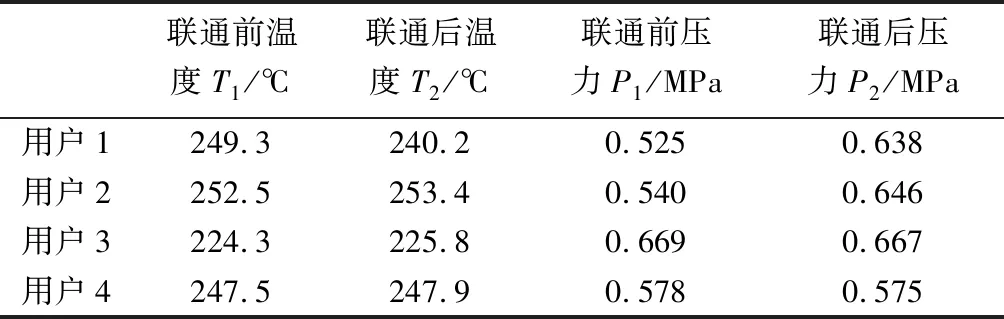
表3 两个管网末端联通前后代表性用户参数的仿真计算结果

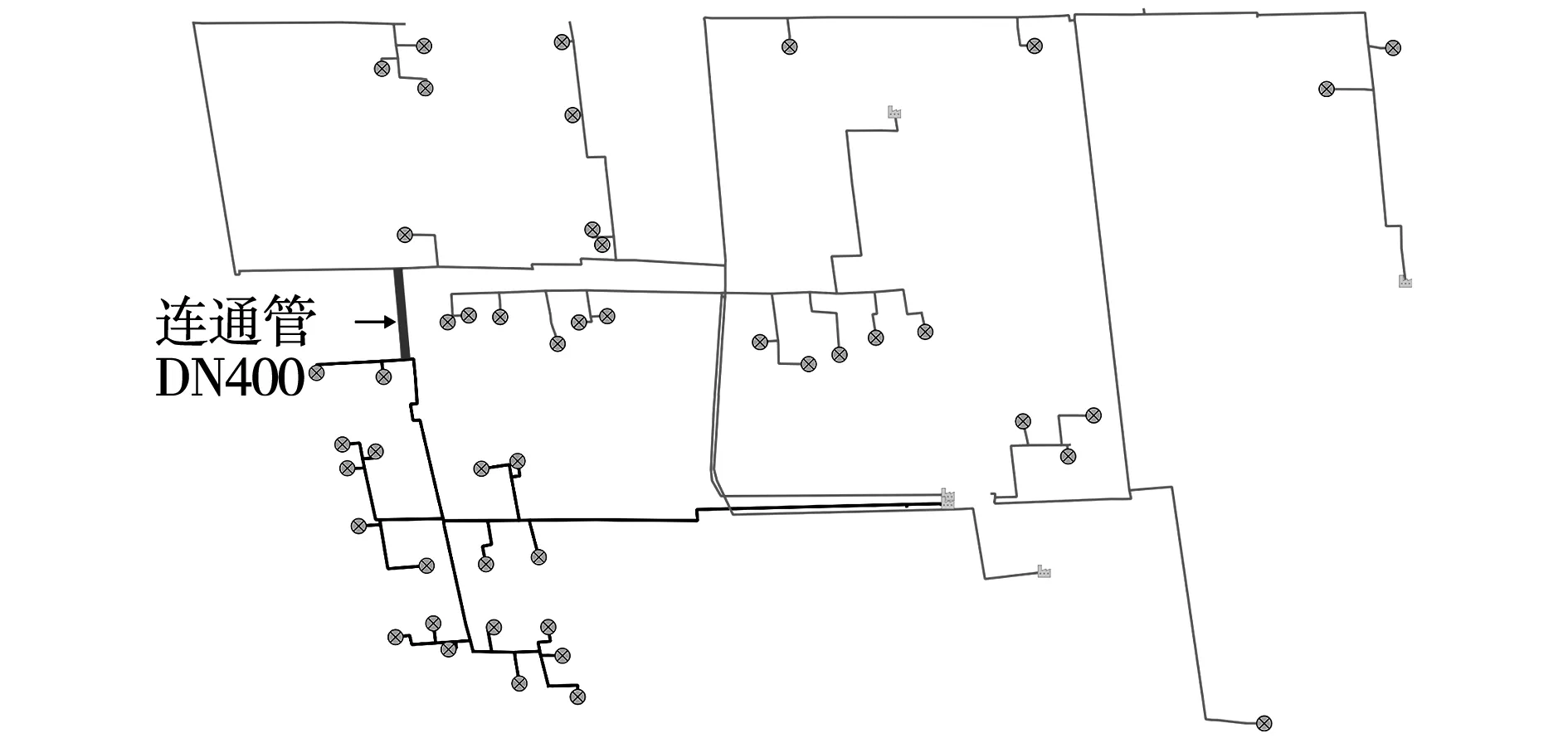
图7 新建管段联通管网1与管网2末端

2.3.2 改造方案实际工程验证

基于前述优化结果建造联通管线后，本文对管网1和管网2通过DN400的管线进行联通前后的代表性用户的实测参数变化结果进行了基于实测数据的总结对比，这一结果总结于表4。

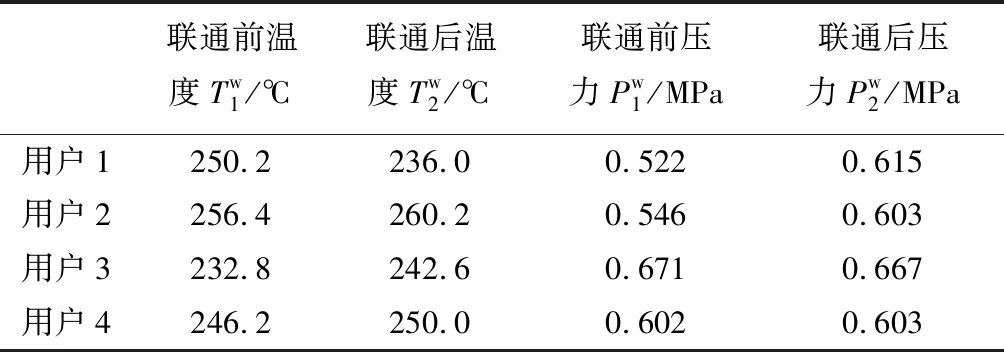
表4 两个管网末端联通前后代表性用户的实测参数变化

由表4结果可知，虽然联通后的工况由于用户使用流量的变化以及源侧参数的变化，实际结果与计算结果略有不同，但趋势基本保持一致：管网1末端用户的压力抬升明显，同时管网2的用户侧压力基本没有变化；而用户1如仿真预期的那样发生了明显的蒸汽温度降低现象。结果表明，基于模型做出的一系列改造方案，达到了预期的效果。在本次的仿真辅助决策的过程中，将管网1和管网2的末端联通，从而抬升管网1用户的压力的预期效果与平台计算的结果相同；同时平台成功预测管网1与管网2末端连接后，导致的用户1温度下降的不利现象，在实践中对于实际决策过程的利弊权衡提供了更加全面的数据支持。

3 结论与展望

本文首先给出了工业园区蒸汽管网机理模型并建立了以粒子群优化算法为核心的管网优化改造方法。这一方法基于所开发的模型，在不抬高源侧供汽压力和保证管网安全稳定运行的前提下可用于寻找能提高管网整体供汽性能的最优改造方案。本文以绍兴某热电公司运营的蒸汽热网为案例验证了这一建模加优化的蒸汽热网改造新思路的可行性。通过对仿真结果进行分析，得出以下结论：

(1)本文所建立的蒸汽热网模型的仿真结果与实测数据误差小于5%，最高温度误差为4.34%，最高压力误差为3.38%，满足工程精度要求。

(2)基于模型与优化的蒸汽热网改造方法用于案例热网后，显著地提升了部分用户的末端用汽压力，能有效解决蒸汽热网随用户数目增多而导致的局部用汽压力下降的问题。

(3)根据优化改造方案完成现场实际改造后，实测数据显示，典型用户的压力变化与仿真的预测结果趋于一致，验证了这一仿真优化结合的改扩建决策方法的可靠性。

本文通过实践证明，在工业园区蒸汽供热系统仿真分析与决策优化中，“基于模型做预测，基于预测做决策”的理念能发挥其相应的作用。一方面，通过对满足精度要求的模型进行针对改造方案的粒子群算法优化，可以获得预期的操作结果，这避免了实地操作尝试所带来的无法预估的风险和经济损失，提升了决策效率，降低决策成本。另一方面，工业园区供热系统仿真分析提供了更加全面的数据支持，对于工业园区整体权衡利弊起到了有效的辅助作用，对于决策中可能存在的问题，进行展示和反馈，规避实际操作风险，保证用户用汽品质，提高工业园区服务质量。