在活动体验中落实数学核心素养
——以高三数学“函数的单调性和奇偶性”一轮复习课为例
马宝星
(江苏省沙溪高级中学 215000)
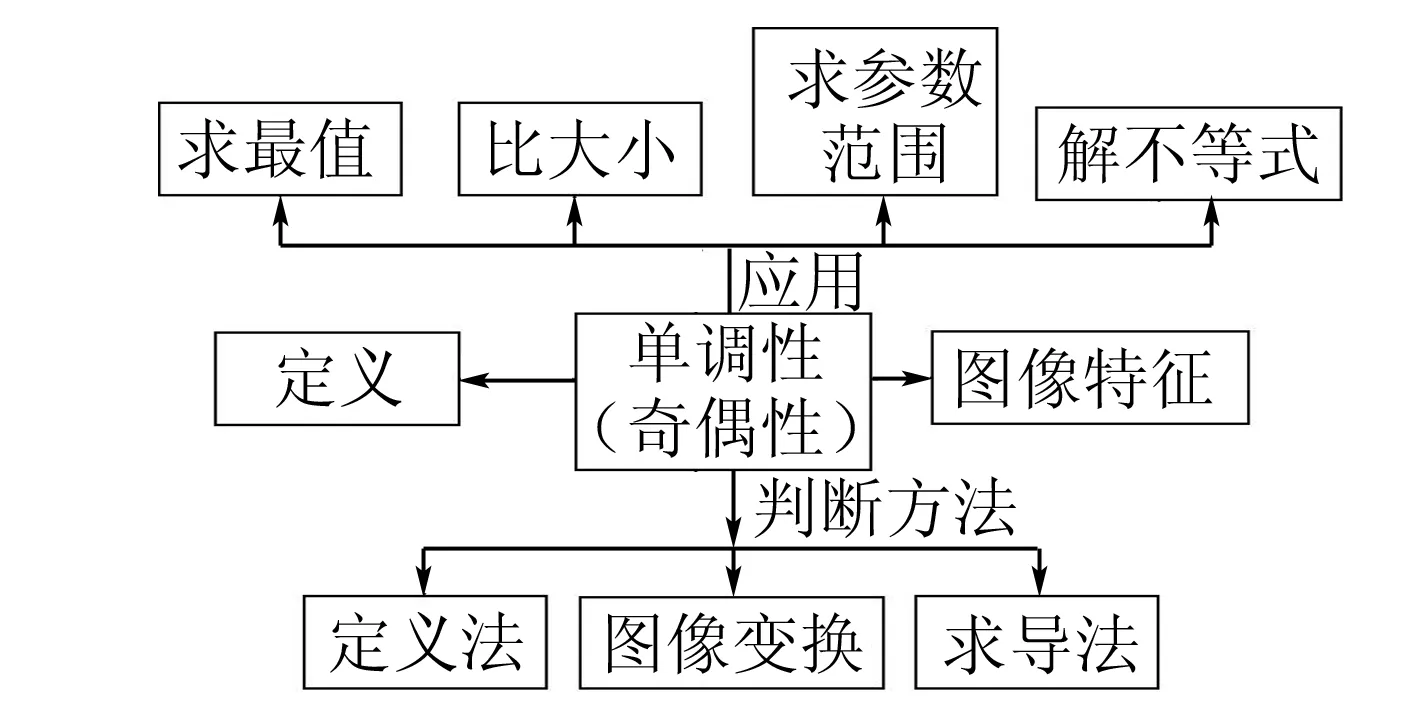
数学教育在不同教学时期都能够提高学生的逻辑思维能力,提高学生辩证思维水平.所以,其课程始终是国内基础教育过程中十分关键的一种学科.新课标明确指出:“利用高中数学的学习,同学们能够得到不断成长和未来发展要求的学科基本知识、基本能力、基本观念、基本活动经验(也就是“四基”);养成从数学视角发现与提出疑问的水平、研究与解决疑问的水平(也就是“四能”).如图,本文在课堂活动中使用思维导图方式, 板书内容追求简练、结构成熟,使人印象深刻.
一、营造开放式课堂氛围,提高学生学习活动的兴趣
在课堂活动中,优良的教学环境能够使同学们在愉悦氛围中逐步提升对于教学活动的认同度,而且让其在优良环境下拓展本身思路,从而能够提高教学速度.然而基于以往教学形式,老师大多会使用灌输式教学方式,只是向同学们传输乏味的数学理论,他们在这种氛围下必定会觉得十分枯燥无味,从而很难提高对于数学的学习热情.然而在实施开放式教学模式过程中,老师重视突破固化的教学环境,建立轻松愉悦的环境.而且使用各种教学方式,使得他们在其中可以提出自己的观点,提高学生的参与热情,这是为了逐步提升他们对于学科知识的参与热情,能够为提高学科素质打下一定的基础.
比如,在巩固《函数的单调性和奇偶性》这一节内容时,笔者以一道高考题为例:
【2020年高考全国Ⅱ卷理数】设函数f(x)=ln|2x+1|-ln|2x-1|,则f(x)( ).
师:说说你们如何判断奇偶性,同学们各抒己见.
生1:利用f(-1)=-f(1)=-ln3,所以它是奇函数;
生2:(立马有同学反驳)不能用特殊值来验证函数奇偶性,而是因为f(-x)=ln|2x-1|-ln|2x+1|=-f(x)成立,所以函数为奇函数.
师:大家认为正确吗?有没有不同意见?
生3:我认为应该先求函数的定义域,定义域要关于原点对称,才是判断奇偶性的前提.
顿时班里出现掌声.在此过程中老师充分地营造了开放式的课堂氛围,课堂中还出现了争先回答问题、相互鼓励、相互赞赏的现象,不只能够让同学们在主动实践、观察阶段中掌握奇偶性的概念和特征,并且能够激起他们对于学科知识的好奇心,这是为了逐步提升他们的学习积极性.
二、开放性问题设计,增加学生数学活动体验
在高中课堂教学活动中,老师大多会讲授很多数学概念、数学习题等,在这一教学阶段中,教学方式在其中有着十分关键的意义.以往教学方式中老师会讲授课本例题,来指导他们了解更多基础概念和答题方式等,然而其方式,必然会使他们逐步形成对于老师的过度依赖,在自己进行学习、解决问题的过程中会觉得没有任何思路,不知如何下手.所以,老师必须在这一阶段中合理使用开放式教学模式,引导同学们通过小组探究协作、自主思考等模式加以学习,这是为了引导他们建立主动解决问题的学习水平,而且这是为了实现提高学生自主思考水平的目标.
比如,本节课以一道高考题为依托,为了充分掌握函数奇偶性和单调性.笔者设计了4个问题情境,
变式1 求函数f(x)=ln|2x+1|-ln|2x-1|的单调区间为____.
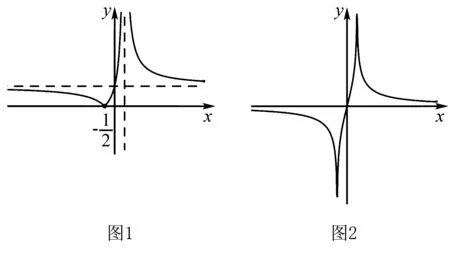
设计意图:设置填空的形式,加深学生对于单调性的概念理解,尤其是两个单调区间用逗号或和连接,通过老师不停追问,为什么不能用∪连接,让学生理解对于任意x1,x2∈D,如果x1 变式2 证明函数f(x)=ln|2x+1|-ln|2x-1|在(-,单调递减,并求y=f(x)在x∈[-2,-1)上的最值. 设计意图:在一轮复习中,证明单调性我们主要利用定义法和导数法,加强对于他们的理解和应用,已知单调性,我们可以求最值,为什么-1处取不到最值呢?进而复习最值的定义. 设计意图:本问题借助函数的增减性和奇偶性求得不等式,本质是回归单调性定义,如果我们把x1 设计意图:如果我们把x1 能够发现,此处指出的问题还是集中于数学概念实质特点方面,使得同学们展开“有结构的研究活动”,属于定向研究问题[2]. 高中数学以提高学生逻辑思维和辩证思维能力作为重要目标的一种课程,因此其在研究课程学习时,大部分以数学练习题当做重要检验方式.基于以往教学形式,大部分老师使用“题海战术”来拓展学生的题型认知范围,然而在开放式教学过程中,老师能够引导同学们从不同视角对待问题.引导同学们在面对复杂题型的数学问题中,能够及时优化答题方向,提升学生的答题速度. 例如【2020年高考全国Ⅱ卷理数】设函数f(x)=ln|2x+1|-ln|2x-1|,则f(x)在(-,单调递减如何判断呢? 生3:通过分析,画出整个函数f(x)=ln(-2x-1)-ln(1-2x)的图像如图2: 生4:通过f(-2)>f(-1),判断它是减函数.(很好,虽然不能取特殊值判断单调性,但是做选择题也不失为一个好方法.) 学生在研究解题方法过程中会逐步建立创新观念,逐步扩大了自身答题思维的涉及范围,这是为了实现开放式教学提高学生发散性思维能力的目标. 从“双基”到“四基”,增加基本思想,基本活动经验,就是为了更好的在数学教学过程中培养学科素养.学生在数学活动体验中,能够让他们提升学习积极性、提高自己的思维能力,引导他们形成良好的创新观念,实现培养他们数学思维水平的目标.数学家莱布尼兹早就说过:数学的本质不在于它的结论,而在于它的思想方法.由此可见,高中数学教师不能简单的告诉学生一些结论,而应该提供丰富的数学活动,使学生在活动中感悟数学本质,为高三数学一轮复习奠定更加坚实的基础.
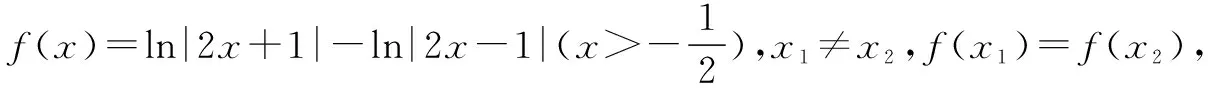
三、激发开放式解题思维,增强学生创新意识