数学情境问题解决错误分析与评价

邓海英，严 卿，魏亚楠

数学情境问题解决错误分析与评价

邓海英1，严 卿2，魏亚楠3

（1．湖南第一师范学院 数学与计算科学学院，湖南 长沙 410205；2．湖北大学 数学与统计学学院，湖北 武汉 430062；3．南京师范大学 数学科学学院，江苏 南京 210046）

在问题解决中，出现错误是不可避免的，错误的合理性正逐渐得到教育工作者的认可，将其看作一种有效的教学资源．情境问题解决与核心素养密切相关，因此，从核心素养的视角出发，构建数学情境问题解决错误分析框架，分析结果如下：（1）在6个数学核心素养成分中，数学抽象、逻辑推理错误出现得最多；（2）数学核心素养三级水平中，被试普遍难以达到二级水平．研究亦得，不理解情境是影响错误的核心因素．教师在教学中应深化学生对情境的理解和培养情境中的知识迁移能力，以促成数学核心素养的培养．

数学情境问题解决；错误分析与评价；数学核心素养；情境

1 问题提出

中国最新颁布的《普通高中数学课程标准（2017年版）》给出了数学核心素养六大成分的具体内涵，并相应划分了三级水平，为数学核心素养培养的水平提供了理论依据和判断标准．大型国际教育测量项目PISA秉持弗赖登塔尔的现实数学教育观（RME），在开发测试体系的时候便提出了“素养”的概念（“不管是哪个国家或地区，不管学生在学校学习的内容是什么，学习的目标应该是培养学生应用知识的能力，使学生能够在实际生活中应用所学知识，进而解决问题”），试题也都基于现实情境，通过学生在不同现实情境下解决实际问题的表现来评价他们的素养[1-2]．PISA测试中有关情境的研究，比较早期的有Chipman等人发现对情境的熟悉度对应用题的表现有很小的正面影响[3]；也有个别研究宣称并不能确定“情境熟悉度”和“正确率”之间的关系是什么[4]；还有从男女性别对情境的不同熟悉度和兴趣对PISA的影响进行的研究，但是这方面的研究还不完善[5]．这些研究主要针对15岁学生（在世界各国大部分已经完成义务教育阶段），小学阶段情形如何还不能确定．

当前核心素养是中国新一轮深化课程改革的主要方向，然而不少一线小学数学教师对核心素养怎么进课堂感到迷茫，不知如何落实．这里不妨借鉴PISA测试的有益经验，将在现实情境中解决问题的能力作为核心素养重要的参考指标，已有国内外学者关注到了现实情境与数学核心素养的关系，认为数学核心素养要借助特定的情境潜移默化方能习得[6]，“让知识学习与多样化的情境相联系，让学生置身真实问题情境、亲历复杂的问题解决过程，可以促进核心素养的培养与发展”[7]．因此，基于PISA和数学核心素养的共同理念，改编PISA试题，选择小学四年级学生（三~四年级是抽象[8]、归纳和演绎能力发展的关键时期[8]．这3种能力是数学核心素养的关键成分）为研究对象，测试在情境中解决数学问题的能力，分析在情境中的错误以及错误原因．分析学生的错误是最重要的、也是最困难的[9]，但依然试着努力去做，希望减少数学错误的发生，为培养核心素养提供有用的教学资源和参考．

2 测试卷的水平划分和指标分析

2.1 测试卷的水平划分

喻平教授认为要发展学生的数学核心素养，就要发展学生的学科关键能力[10]，学科关键能力生成的本源是知识，生成机制是知识理解、知识迁移、知识创新3种知识学习形态，对应生成的结果是学科关键能力的一、二、三级水平[11]．由此，从知识与能力的角度提出评价数学核心素养的框架，即3种知识学习形态对应着学科关键能力的三级水平[12]．情境问题解决也是一种数学能力，知识也是其生成的本源，需要理解、运用知识，甚至带有创造性．所以，测试卷借鉴该框架，将数学情境问题解决水平分成知识理解、知识迁移、知识创新3个等级．

测试卷由数学教育专业教授、研究生和小学数学特级教师根据PISA测试题共同改编完成，参照PISA2012的情境分类，将情境分为个人情境、公共情境、科学情境、教育与职业情境．个人情境聚焦个人日常生活的各个方面；公共情境聚焦公民、地方、国家或全球；科学情境要求学生运用数学知识解决和科学技术相关的问题[5]；教育与职业的情境指与学生的学校生活或工作环境相关的情境[13]．测试共9道大题13个小题，分别简称为登富士山、跑道赛跑、最大心跳率、建筑距离、颜色合成、公园排队、雇佣关系、花圃面积、开车上班．试卷各题项的测试内容、三级水平划分以及情境类型见表1．要特别提出的是，由于情境的复杂性，这些对应不是绝对的，只是给出各题项最相关的情境类型．

2.2 测试卷的指标分析

PISA试题难度要求必须是中等的，所以PISA测试中不会包含难度非常大或者难度非常小的题目．测试题全部由PISA试题改编而来，有必要对试卷难度进行分析，用SPSS 17.0进行分析如表2．

表1 数学情境问题解决试卷各题项水平划分与情境类型

表2 测试卷题项得分与总分的相关系数及试卷难度

表2结果显示，总测试难度系数为0.474，接近中等难度临界值0.4，与PISA难度接近，但存在个别难度较大和较小的题，如题9和题2，但还是在可接受范围之内．（另注：测试卷的3个水平是关键能力的水平划分，并非难度水平划分．虽然二者确实从理论上存在一致性，但并非绝对的．如题4属于知识理解水平，但是理解层次加深，使得难度大于知识迁移水平的题5、6(1)、7(1)(2)；又如题7(3)属于知识迁移水平，情境迁移与(1)(2)小题类似，但是运算方法要复杂一些，使得难度大于知识创新水平的题8．）表2结果还显示所有题项与总测验得分都在0.001的显著水平上相关，每个题项与总分的相关系数在0.239~0.729之间，说明题项与测试卷的测验目标一致，因此保留所有题项．

结果显示三级水平之间的内部一致性系数在0.555~ 0.725之间，总测试的内部一致性系数为0.799，说明该测试卷的总体信度较好．三级水平之间的相关系数小于每个水平与总测试的相关系数，表明该测试卷具有较好的结构效度．同时，一级水平和三级水平之间的相关系数小于一级水平与二级水平，同时也小于二级水平与三级水平，说明3个水平的等级划分是合理的．

由以上分析得到，此次测试卷难度、信度、结构效度等各项指标都较好，为下文分析、评价错误提供了合理的前提．

3 数学情境问题解决错误分析框架

对数学核心素养各成分三级水平的描述[14]进行归纳，作为数学情境问题解决错误的分析框架见表4．通过这种框架的建立，旨在发现数学情境问题解决典型错误的水平分布．

表3 测试卷题项克伦巴赫a系数和结构效度

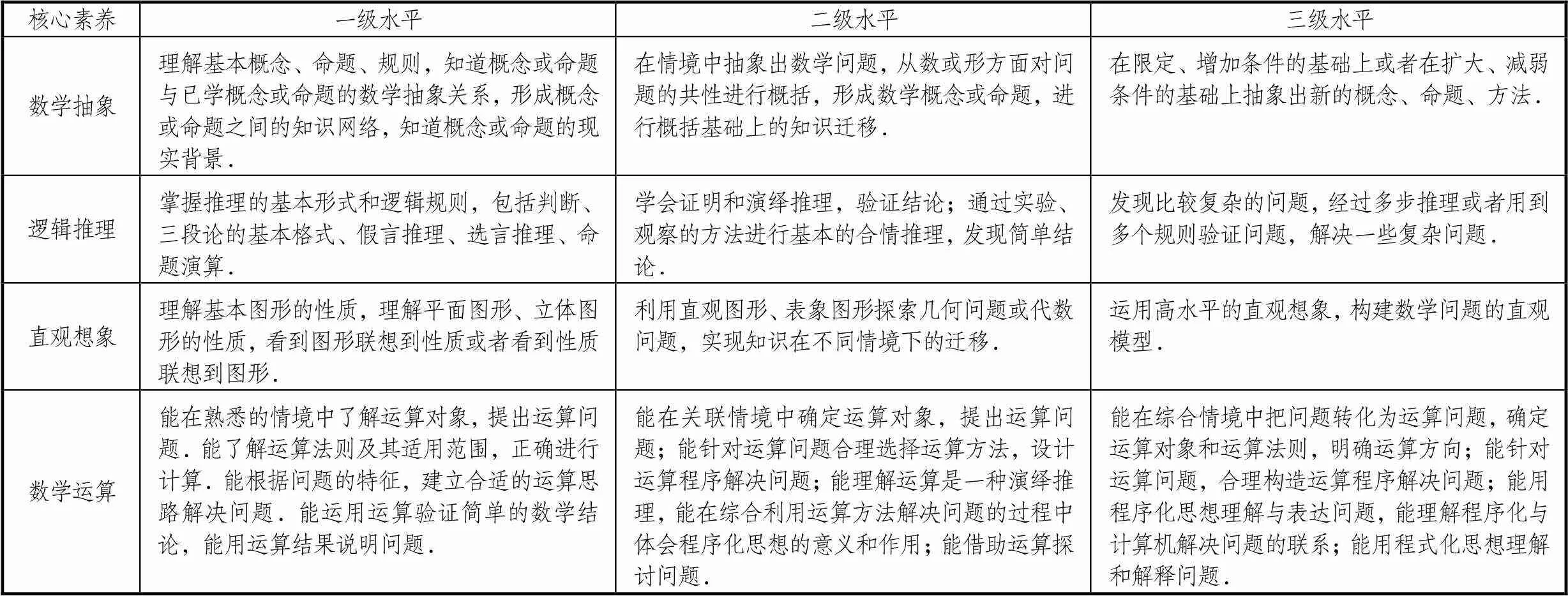
表4 数学核心素养的三级水平划分与内涵

表4（续） 数学核心素养的三级水平划分与内涵

4 数学情境问题解决典型错误分析

4.1 题项错误率统计

表5 数学情境问题解决测试失分统计

表5数据说明出错的人次很多，题目错误率也很高，每道题都有人做错，4种情境出错的程度不一．以下给出如图1所示4种情境出错人数率的散点图（横轴1~13为13个小题题号，纵轴0~100为省去百分号的出错人数率）．

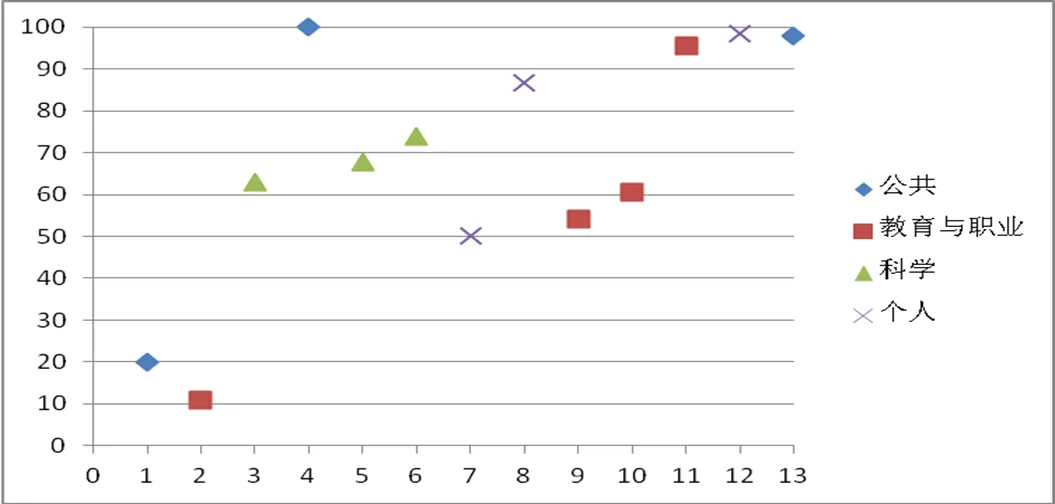
图1 4种情境出错人数率

从图1可看出，此次测试人数出错率内部相对最稳定的是科学情境，其次是个人情境，波动最大的是公共情境，其次是教育与职业情境，13个小题的出错人数率均值67.62%，方差0.085，总体上看，出错人数率随题号往后有一定的上升趋势．

4.2 题项错误分析

题1：登富士山．

此题除去没有作答，错误结果还有280 000、270 000、210 000、27 000、1万、8 971、9 000、4 500、4 000、3 400、3 000、2 700、2 100、1 000、999、900、700、540、500、430、360、388、344、321、320、310、270、261、200、114、100、94、56、51.83、38、35、31、30、6、4.93、3等．除了可能因为粗心产生的计算错误或者题意弄错之外，反映了典型错误：被试对登富士山的情境不熟悉，因而不能将情境中的总天数、总人数正确转化为求平均数的条件．甚至还出现了人数为小数的情况．这类典型错误指向数学抽象一级水平不足，同时还缺乏基本的逻辑推理能力．

题2：跑道赛跑．

该题除了没有作答和填了时间“9.87”之外，还出现了一些非常“奇特”的答案：出现了15次“1”，3次“2”，4次“4”和1次“5”（这些被试在不同学校或同校不同班，答案纯属巧合）．典型错误：被试可能不熟悉跑道赛跑的情境，不知道时间与排名的关系，而是错误地运用了个人经验，比如认为位于跑道1或5的选手占据了跑道优势，所以跑起来更快．这类典型错误指向逻辑推理一级水平不足，而填了“2”或“4”的被试有可能是因为3与2和4相邻，所以粗心误填，观察能力不够强．

题3：最大心跳率．

题4：建筑距离．

该题错误答案分成4类：给出了最大值和最小值、给出最大值或最小值、无作答和作答全错．典型错误：被试对三点距离知识和3个建筑的“位置情境”都缺乏全面的理解，将“两点共线”错误迁移至“三点共线”，错误的知识产生错误的迁移，没有建立起直观的三角模型与建筑实际位置进行对应．这类典型错误指向直观想象的二级水平和数学建模的二级水平不足．对于只给出一个值的被试，其直观想象不足二级水平，数学建模不足一级水平．没有作答或逻辑不清的样本则尚未达到直观想象和数学建模的一级水平．

题5：颜色合成．

该题是科学情境．从错误的答题过程来看，存在典型错误：尽管学生可能认识数组，但是不少被试理解不了题中数组的构成（比如数字大小和排列顺序）与颜色的关系，不能给出完整答案，或是只能给出数组中的个别数字，并且顺序还不一定对，不能完成知识的情境迁移．这类典型错误指向数学抽象二级水平、数学建模二级水平、数据分析二级水平和逻辑推理的三级水平等多种水平的不足．

题6：公园排队．

该题主要错在没有作答或者部分知识点正确．典型错误：将知识迁移到现实情境中时没有弄清题目条件和问题之间以及多个条件之间的关系，逻辑不清、缺乏条理，不能实现点分线段到游客排队情境的迁移，导致不能正确列式，个别被试列式正确但计算错误．这类典型错误指向数学抽象二、三级水平，逻辑推理三级水平，直观想象二级水平，数学运算二级水平等多种水平的不足．

题6(2)存在的典型错误，除与题6(1)相似的几种外，还出现了被试没有列式101-1=100的错误，也是没有在排队的情境中联想到“植树原理”．这类典型错误指向数学建模二级水平的不足．

题7：雇佣关系．

题7(1)出错的被试除了没有作答，错误的理由各异：比如因为小菊工作时间长，干活久，所以选小菊；因为6+5=11<8+4=12，所以选小兰；虽然小菊种花慢，但是种得好，所以选小菊；还有更多的被试没有理由，就写个小菊，等等．典型错误：被试对工作效率不理解，不能将效率的意义迁移到雇佣关系情境中，甚至还产生了误区：工作时间越长，所以做得越多，没有理解这里是单位时间．题7(2)本质上也是计算工作效率．这两个题项反映的典型错误类似，都是在表格表示的方法下，对工作效率与工作时间、工作总量、单位工作量之间的关系不清楚．这类典型错误指向逻辑推理一、二级水平和数据分析一、二级水平的不足．

题7(3)相比起题7(1)、7(2)，比较工作效率的情境要复杂一些．这道题除了因工作效率概念不清、算法出错和其它各种具有偶发性的错误之外，有一类错误非常典型，见图2．

图2 典型错误

图2中右边解答思路是对的（但220计算错误和作答结论出错）．这次测试中有11.3%的被试得出了96和80的结果，具体过程举例如图3所示．

图3 解答举例

这种错误的解答在于少乘了两次10，原因是被试对较复杂情境下的多步乘法理解不透彻．题7(3)的典型错误还应包括逻辑推理三级水平和数据分析三级水平的不足．

题8：花圃面积．

该题属于个人情境，题目已给出代表花圃的平面图形矩形，帮学生完成了抽象的第一步，只有13个被试给出了3种及以上的分法，有一定的创新能力，少部分被试能给出一到两种分法，有欠创新．一半的被试没有作答或者只是在矩形上思路不清地点画了几笔，这些学生不明白矩形的用途，没有将三等分花圃的面积转化为三等分矩形的面积，情境迁移失败，更无从谈分法创新．典型错误：被试将实物转化成平面图形的知识迁移水平非常不足和探索几何问题的创新能力也相当缺乏．这类典型错误反映数学抽象的二级水平、直观想象的二级水平有很大欠缺．

题9：开车上班．

此题中开车时间会因等待红绿灯的不同而变化，是一个变化的量，但是学生对此不敏感，视红绿灯等待时间为无用的数据．只有17个被试完成要求，其他很多被试没有作答，还有不少被试没有设计情境，只是按照常规思路求出了蔡老师的家到办公大楼的距离或中间某一段距离等，与题意不符，还有少部分被试“陷”在多步运算中“跳”不出来，思路和计算都不对．典型错误：学生对真实的复杂生活情境缺乏经验，限制在书本的理想情境里，形成思维定式、缺乏创新．此题的典型错误指向数学抽象、数学运算和数据分析的三级水平不足．

4.3 典型错误水平分布

对上述错误水平进行频数统计，得到错误水平分布表如表6所示．

表6 数学情境问题解决错误水平分布

从表6可以看出，数学抽象、逻辑推理是典型错误出现得最多的两个数学核心成分，数据分析次之．另外，除了逻辑推理之外，其它5个数学核心素养成分各自三级水平出错最多的都是二级水平．

5 结论

国际上对影响学生PISA成绩的因素做了一些宏观的分析：社会阶层[15]、教育公平和学校环境等[16]，这些因素也可能是学生在PISA测试中出错的间接原因；学生的粗心、观察能力不强、策略[17]不足等，也是错误产生的重要原因，在此次测试中普遍存在．此外，学生的自我效能感、焦虑等[18]也是学生出错的心理等原因．下文根据题项错误分析，从情境的角度总结错误原因．

（1）情境类型之间没有难易之分．

通过上文4种情境错误人数率散点图可以看到，每个情境类型中都有不同层次的人数出错率，4种情境类型之间没有难易的区别，不能肯定学生会在哪个情境中更容易产生错误．

（2）不熟悉情境加重认知负荷．

（3）不理解情境影响迁移和创新．

熟悉情境并不一定就理解情境，不熟悉的情境在知识的充分理解下也能理解情境．因此，理解情境是解决问题的关键，对情境的理解是迁移和创新最基本的前提．如学生理解不了题5的科学情境，同时也失去了数组知识迁移的方向和目标．又如题9要求学生根据条件“创设情境”，这本身就置学生于一种“动态”的问题解决情境之中，但是学生对由题目条件而生可又不是“现成”的“情境”不理解，因此不能创新．

（4）对情境不感兴趣影响正确率．

测试之余，对学生进行了问卷调查，其中有如下问题“你觉得刚才做的测试卷题目很有意思吗”“你对有故事情节的数学题目很感兴趣吗”涉及到学生对题目的兴趣，其实质也是学生对试题情境设计的兴趣．问卷结果显示，学生对试题情境的兴趣与测试成绩呈现弱相关性．学生对情境的兴趣会影响他们解题动机和毅力等，正面的作用会激励学生，负面的作用则会让学生变得消极，比如放弃作答或者敷衍了事，从而增加错误．

Chipman等人指出学生对情境不感兴趣的情况最容易发生在学生不熟悉情境的时候[3]．用图4表示情境类型、熟悉、理解、兴趣四因素之间的关联：对情境的理解占据中心地位，同时受情境类型、熟悉度的制约；类型和熟悉度影响兴趣，但是对情境很好的理解又可以改善对情境不熟悉和不感兴趣的状况．因此，不理解情境是学生出错的首要原因．

6 启示与建议

（1）创设多样化的情境，深化理解．

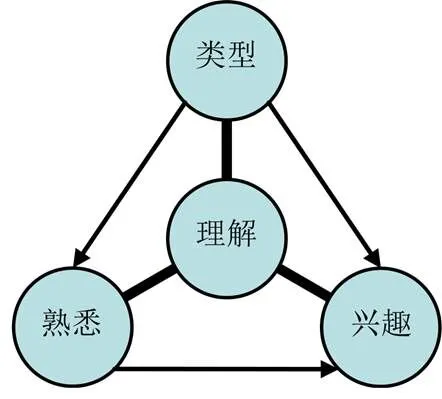
图4 四因素关联图

教师在教学中要创设多样化的、合理的情境，并要深化理解，而不只是为了“装饰”停留在表面．如何深刻理解情境？能够判别情境倾向哪个类型、是纯数学的还是现实的，这是最基本的要求，更重要的是要理解这个情境用到什么知识、解决什么问题，主要方法是什么？归根结底，首先还是要加强对知识的理解，除了“4个基本理解”（知识的基本性质、基本事实和结论、基本概念和规则以及基本方法），还包括了解知识的源头、形成概念和命题体系、理解规则和法则的结构以及使用条件等3个较高的要求．只有深层次的理解，抽象出知识的本质属性，才能实现在情境中的灵活运用．典型例子如题4，所有被试都没有深刻理解在不同条件下的求距离的方法，存在“知识盲点”而造成了普遍的错误．

（2）提高情境中的知识迁移能力，发展数学核心素养．

表6显示，数学核心素养各成分的二级水平出错最多，学生也就达不到相应的三级水平．表4也显示，数学核心素养各成分的二级水平较普遍地涉及到了知识迁移．这为培养数学核心素养提供了一条思路：提高情境中的知识迁移能力即能促进数学核心素养的发展．表4中二级水平的内涵从知识的角度概括了在情境中迁移的目标，在教学中可结合具体教学内容进行实践，促成目标的达成．如题7，在教学中应让学生理解“工作效率”的实质，掌握总工作量、总工作时间和单位工作量这3个要素之间的相互转化关系和等价作用，再实现在不同情境中的迁移．

（3）重视数据分析能力的培养，与时俱进．

当今社会，数据已经渗透到各个行业．从情境的角度看，数据的主要来源是客观现实世界，任何数据不仅仅是包含数量、文字、符号、图形等抽象信息，必然还包含了与现实情境有关的背景信息，这些背景信息中的人或事物就构成了数据的情境[20]．如题9，“每个红绿灯的等待时间2分钟”是一个非常关键的条件，既是数学的信息，也是情境的信息，是一个典型的“情境数据”，但是学生几乎都忽视了．教师对这样的问题应该多分析情境中的数学信息，善于抓住“情境数据”，帮助学生改变对“数据”的狭隘理解．此外，要培养学生的数据分析能力，必然要发展学生的阅读能力，不但是要能看“文字”，还要能读懂题中的数量、符号、图象等一切能够承载事物信息的载体．当然，发展学生的数据分析能力不能急于求成，教师应按部就班，提供现实情境中的典型案例，让学生随着学龄的增长，经历建立数据分析意识—掌握数据分析方法—积累数据分析经验的学习过程，逐步形成数据分析素养．

（4）加强培养数学抽象和逻辑推理能力依然是根本．

抽象能力和逻辑推理能力是思维品质深刻性的重要指标．通常在教学中，教师可展示数学抽象的情境背景以降低抽象层次，反过来又影响学生在情境中抽象出数学问题的能力，让学生学会剥离情境中的非本质属性，逐步实现“去情境化”，最终脱离较低层次的情境支持而发展成独立的数学知识．逻辑推理的依据是“事实”和“命题”，是建立在情境基础上的思维过程[20]，现实情境或纯数学情境是培养学生逻辑推理能力的有力支撑，可以启示学生不必犯一些“低级”错误，如题1中的登山人数绝对不可能是小数．很多时候，学生逻辑推理素养的形成，在本质上不是靠教师“教”出来的，而是靠学生自己“悟”出来的[21]，合适的情境就是一个“悟”的好环境．

数学情境问题解决需要学生多种核心素养在情境中共同作用，是一种较高水平的数学素养．测试结果显示四年级学生在六大核心素养上水平欠缺，对教师而言，明确数学核心素养的内涵、各成分三级水平的划分，了解国际先进教育思想，形成科学的知识观、数学观，是培养学生数学核心素养的必备素质；在数学教学中合理对待学生的错误，化“错误”为资源，以“错误”促教学，是正确的教学态度；了解情境与核心素养的密切关系，发挥情境在培养数学核心素养中的作用则是有效的教学策略．

[1] 陈敏，杨玉东．小学生解决真实情境问题的调查研究——基于PISA数学素养的视角[J]．上海教育科研，2016（9）：46–49，54．

[2] OECD. What is PISA [EB/OL]. (2018–02–06) [2019–07–09]. http://www.oecd.org/pisa/aboutpisa/.pdf.

[3] CHIPMAN S, MARSHALL S, SCOTT P. Content effects on word problem performance: A possible source of test bias [J]. American Educational Research Journal, 1991, 28 (4): 897–915.

[4] DE LANGE J. Large-scale assessment and mathematics education [M] // LESTER F K. Second handbook of research on mathematics teaching and learning. Charlotte: Information Age Publishing, 2007: 1 112–1 142.

[5] STACEY K，TURNER R．数学素养的测评——走进PISA测试[M]．雷一鸣，译．北京：教育科学出版社，2017：30．

[6] LENGNIK K. Reflecting mathematics: An approach to achieve mathematical literacy [J]. ZDM the International Journal on Mathematics Education, 2005, 37 (3): 246–249.

[7] 张华．论核心素养的内涵[J]．全球教育展望，2016，45（4）：1–15．

[8] 林崇德．智力发展与数学学习[M]．北京：中国轻工业出版社，2011：185．

[9] 郜舒竹，刘莹．儿童数学学习中思维的自然结构及其正误辨别[J]．课程·教材·教法，2010，30（7）：42–45，76．

[10] 喻平．发展学生学科核心素养的教学目标与策略[J]．课程·教材·教法，2017，37（1）：48–53，68．

[11] 喻平．学科关键能力的生成与评价[J]．教育学报，2018，14（2）：34–40．

[12] 喻平．数学核心素养评价的一个框架[J]．数学教育学报，2017，26（2）：19–23，59．

[13] 陈慧，袁珠．PISA：一个国际性的学生评价项目[J]．外国中小学教育，2008（8）：53–58．

[14] 喻平．数学核心素养的培养：知识分类视角[J]．教育理论与实践，2018，38（17）：3–6．

[15] COOPER B, DUNNE M. Anyone for tennis? Social class differences in children’s responses to national curriculum mathematics testing [J]. The Sociological Review, 1998, 46 (1): 115–148.

[16] 陆璟．PISA测评的理论和实践[M]．上海：华东师范大学出版社，2013：127–148．

[17] 李清，王菡．元认知策略、解题策略对不同层次学生数学问题解决影响的实证研究[J]．教育理论与实践，2017，37（35）：41–43．

[18] 刘星辰，原露，陈启山．数学焦虑与数学自我效能感对数学素养的影响：来自PISA的结果[J]．考试研究，2016（2）：89–94．

[19] 陈燕，罗增儒，赵建斌．从认知负荷理论看数学错误[J]．数学教育学报，2009，18（4）：19–22．

[20] 常磊，鲍建生．情境视角下的数学核心素养[J]．数学教育学报，2017，26（2）：24–28．

[21] 史宁中．试论数学推理过程的逻辑性——兼论什么是有逻辑的推理[J]．数学教育学报，2016，25（4）：1–16．

Identification and Analysis of Mathematical Errors in Solving Contextualized Problems

DENG Hai-ying1, YAN Qing2, WEI Ya-nan3

(1. School of Mathematics and Computational Science, Hunan First Normal University, Hunan Changsha 410205, China;2. Faculty of Mathematics and Statistics, Hubei University, Hubei Wuhan 430062, China;3. School of Mathematical Sciences, Nanjing Normal University, Jiangsu Nanjing 210046, China)

In problem solving, making errors are inevitable. The appropriate use of mathematical errors has gradually been recognized by educators as an effective teaching resource. Contextualized problem solving is closely related to key competency in mathematics. This paper developed a framework for error analysis of in solving contextualized mathematical problems. It is found that: (1) Among the six components of key competency of mathematics, mathematical abstraction and logical reasoning errors occur most frequently; and (2) in the three levels of key competency of mathematics, it is generally difficult to reach the second level. Research has also shown that the key factor in error making is not understanding the context. Teachers should deepen students’ understanding of the context and cultivate their ability to transfer knowledge in the context to promote the cultivation of mathematical key competency.

mathematical contextual problem solving; error analysis and evaluation; key competency of mathematics; context

附录：测试题

1. 每年的7月1日—7月30日富士山对公众开放，在这段时间里，大约有9 000名游客去富士山爬山，平均每天大约有名游客．

2. 学校刚刚举行了秋季运动会，短跑竞赛的竞争非常激烈．下表列出了进入决赛的5名同学的短跑成绩，则跑道的同学是冠军．

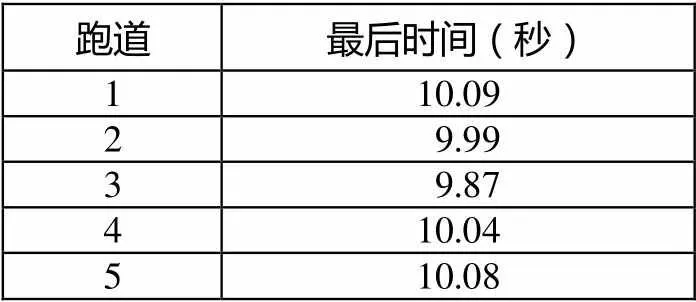
跑道最后时间（秒） 110.09 2 9.99 3 9.87 410.04 510.08

4. 体育中心距离学校17千米，一大型超市距离学校8千米，请问体育中心和超市有多远？

5. 红色、绿色和蓝色被称为光的三原色．在电子设备中我们通过调节这3种颜色的亮度表示其他颜色．用3个255以内的整数分别表示红色、绿色和蓝色的亮度，数字越大代表亮度越高．例如：(255, 0, 0)是指红色，(0, 255, 0)代表绿色．(0, 255, 255)表示红光亮度0、蓝光亮度255、绿光亮度255，合起来就是标准青色；(200, 0, 150)表示红光亮度200、绿光亮度0、蓝光亮度150，合成的颜色是偏红的紫色．(255, 255, 255)表示红光亮度255、绿光亮度255，蓝光亮度255合起来是白色．红色和绿色可以合成黄色．标准黄色可由亮度最高的红光和最高的绿光合成，请问：

（1）如何表示“标准黄色”?（2）如何表示“偏红的黄色”？

6. 小明的爸妈趁着假期带着小明和妹妹到花博园游玩．园内人山人海，每个展馆几乎都要排队．大家讨论决定要去参观梦想馆和流行馆．每个展馆的排队方式都是两人并排，地面画有小型圆圈，工作人员会请排队人群站在小型圆点上，以便统计人数．如右图：

问题（1）：首先，小明一家人来到梦想馆，小明他们所排位置旁的告示牌写着离入口处大约需要2小时．而工作人员平均每十分钟放30人同时入场，请问排在小明一家人前面的大约有多少人？

问题（2）：小明一家人来到流行馆．小明发现排队位置上写的第101排，而工作人员平均约每10分钟开放20人同时入场．请问，小明一家人还要等多久才能够入场？

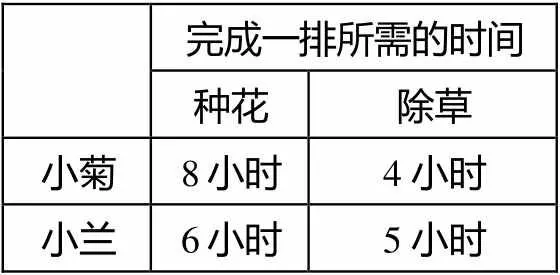
完成一排所需的时间 种花除草 小菊8小时4小时 小兰6小时5小时

7. 小菊和小兰应征园丁的工作，花园老板发现二人的工作态度都很好，对薪水的期待也相同．在完成一件需要种花和除草的工作中，老板比较二人种花和除草所需的时间如右表，请回答下列问题：

问题（1）：如果你是花园的老板，需聘用一位专职种花的人，每天工作10小时，你会请哪一个人帮你种花？请说明理由．

问题（2）：如果花季的临时工，工资是以种花或除草的数量计算（例如种花或除草的工资都是5元/株），就小兰而言，同样的加班时间，她应该选择种花还是除草的工作赚得比较多？

问题（3）：如果你是花园的老板，只能聘用一人负责种花与除草，若一个月的工作约需种10排花、每排要除4次草，你会聘用谁？请说出理由．

8. 翰子老师有一块长方形的花，长15米、宽10米，如下图：

将花圃以长方形表示，=15 m，=10 m．若翰子老师欲将郁金香、百合花、玫瑰花分別种满花圃总面积的1/3，则有什么方式可以将此花圃面积三等分？请你帮翰子老师设计一下．（至少两种方案，越多越好）

9. 蔡老师上班的概况如下，家里大门口出发到第一个红绿灯下约2 km，再开到第二个红绿灯下约3 km，第二个人红绿灯即上高速公路，路程约15 km，下高速公路后，会遇到第三个红绿灯，再开到上班的办公大楼约20 km，这之间还有一个红绿灯．蔡老师遵守交通规则，平常开车习惯是：一般限速70 km/小时的道路，蔡老师会开60 km/小时，高速公路限速110 km/小时，蔡老师会开100 km/小时．道路红绿灯需要等2分钟．

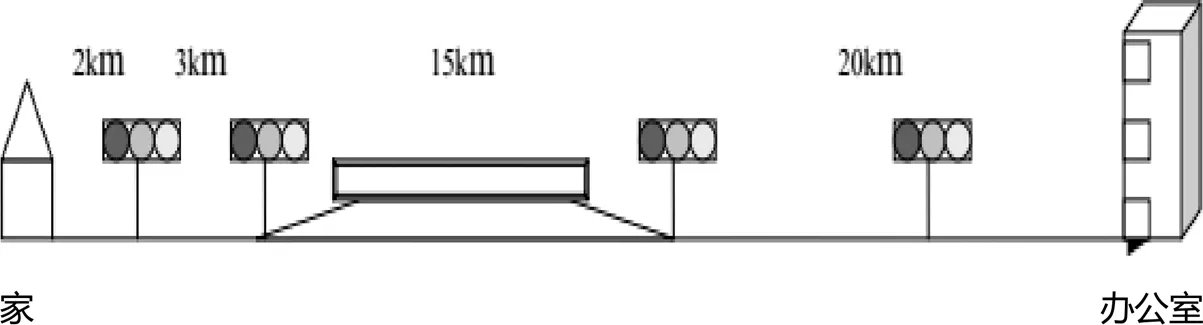
请根据以上信息，自己设计一个情境，可以增加条件，提出一个数学问题并解答．

G622

A

1004–9894（2021）01–0061–07

邓海英，严卿，魏亚楠．数学情境问题解决错误分析与评价[J]．数学教育学报，2021，30（1）：61-67．

2020–10–09

湖南省社会科学成果评审委员会项目——小学生情境问题解决能力培养研究（XSP21YBC052）

邓海英（1982—），女，湖南邵阳人，讲师，硕士，主要从事课程与教学论和小学数学教育研究．

[责任编校：周学智、张楠]