基于GA-BPNN 的采后蜜桃预冷效果预测模型

谌英敏，王 贺，苏 勤，赵 锐，宋海燕※

（1. 山西农业大学农业工程学院，太谷 030801； 2. 南京农业大学工学院，南京 210031）

0 引 言

蜜桃是一种典型的呼吸跃变型球类果实，采摘季节主要集中在炎热多雨的6－8 月。在此期间，新鲜采摘的蜜桃含有大量田间热，这导致果实较高的呼吸强度和乙烯释放量，加速了新陈代谢和后熟速率，从而使蜜桃耐贮藏性较差和易腐烂[1]。有研究表明采后蜜桃延迟6 h 后冷却会使多种营养成分损失严重[2]，也会减慢果实移入冷藏库后的冷却速度[3]，而快速通风预处理可减轻桃的挤压机械伤强度[4]，也可提高贮运品质和抗氧化性[5]，其冷却时间比低温预冷少了1/3～4/5[6]。因此，为降低高田间热对果实质量的影响，成熟蜜桃采摘后在冷链物流前需进行快速通风预冷以最大程度提高产品商业经济价值。

计算流体力学（Computational Fluid Dynamics，CFD）可通过求解偏微分控制方程来模拟流固耦合现象，高精度观测果实在预冷过程中的微观变化。然而，预冷试验只能进行现场测试以实现果实预冷效果的宏观分析，而无法微观监测果实内部传热传质及空气流动情况，而且物理试验的循环测试也会浪费大量人力物力资源。由此，CFD 技术常用于果蔬采后预冷研究中，如Berry 等[7-9]采用该技术模拟了苹果的对流换热，但这些模型却忽略了果实内部热源项对预冷流场的影响。Han等[10]发现在CFD数值计算中单个苹果的呼吸热对温差的最大影响仅为0.033 K，建议苹果内部热源可忽略不计。但对于蜜桃、草莓等易腐烂果实而言，其新陈代谢更旺盛，有研究表明在相同预冷环境下蜜桃呼吸热约为苹果的两倍[11]，Nalbandi 等[12]发现在数值计算草莓预冷过程时蒸腾热的加载可缩短31%的预冷时间。由此发现，呼吸热和蒸腾热这两种热源程序的同时加载对提高易腐烂果实预冷过程的预测精度非常关键。然而，目前学者主要分析了桃在冷藏过程中的贮藏时间和感官品质[13-14]，却较少建立蜜桃在强制风冷过程中的传热传质动力学数值模型，也甚少研究不同包装工艺和预冷工况条件下蜜桃的预冷效果。此外，虽然通过CFD 数值模型可获得高时空分辨率下的热传递和气流分布数据，但不能直观显示果实整体预冷均匀性和冷却时间等预冷效果。不便于快速控制冷却时间以实现果实及时有效冷藏转移，从而增大了预冷能耗成本，延长了果实跨区域销售的周转时间，也难以实时调控预冷环境参数以保障果实预冷品质。

因此，为了实现冷藏转移时间的精准监控，提高多层装蜜桃的预冷效果，减少现场试验循环测试成本，本文建立了包含衬垫和内部热源项的 CFD-WIHS（ Computational Fluid Dynamics-With Internal Heat Source）传热传质数值模型，并结合试验数据验证了该建模的准确性，然后通过样本数据，基于遗传算法优化反向传播神经网络（GA-BPNN，Genetic Algorithm-Back Propagation Neural Network）构建了采后蜜桃预冷效果网络预测模型。该模型为后续学者研究蜜桃预冷特性提供了建模依据，为中小型果园商业开发球类果实预冷决策自动化监测系统以降低预冷成本、实现果实快速冷藏转移和保障果实预冷品质提供理论依据。

1 材料与方法

1.1 试验材料

2020 年7－8 月期间，每天从山西省晋中市太谷区（112°55′E，37°43′N）采摘36 个直径约为80 mm 的大久保蜜桃，并在采后2 h 内进行强制风冷试验，如图1 所示。蜜桃果肉半径1/2 处温度由温度数字记录仪（SSN-13E，深圳宇问加壹传感系统有限公司生产）采集，监测误差为±0.3 ℃。在预处理前先启动超声波加湿器（HS-05-3，中国无锡洛社华盛公司生产）使预冷装置内部空气相对湿度保持在90%以上，然后通过操作温度控制界面（冷凝机组由北京京辉源制冷设备有限公司组装）动态调控内部流动空气温度，风道内空气震荡幅度为±1 ℃；调整风机频率确定空气流入速率，风速值由风速检测仪（PR-3000-FSJT- V05）监测，误差为±0.3 m/s，精度为±0.1 m/s。

1.2 建立CFD-WIHS 传热传质预冷模型

1.2.1 物理模型与网格划分

经过市场调研及文献参考发现苹果、番茄、蜜桃等球类水果，市场上常以瓦楞纸箱包装为主来进行通风预冷[7-8,11,15-18]，开孔数主要为2、4、6 和9，开孔直径范围20～40 mm；而荔枝、枸杞等小型果实或杏鲍菇等蔬菜常以塑料筐包装为主进行冰水或真空等其他方式预冷[19-22]。因此，本文采用双层加固型瓦楞纸箱，并结合实际市场应用情况，针对开孔数2、4、6 和9 进行物理建模。外包装几何规格为428 mm×300 mm×300 mm，厚度为7 mm，衬垫为368 mm×256 mm×4 mm 的单层瓦楞纸板，结构如图2所示。所有箱体侧面开孔率范围为0.70%～12.56%，占总包装面积的0.18%～3.26%，远低于瓦楞纸箱通风总面积要低于总包装面积3%～5%的包装结构设计要求；该箱体长宽比符合1.5∶1 的包装工程要求[23-25]，这使瓦楞纸箱具有较强的机械强度和托盘稳定性。

利用Meshing 软件对箱内蜜桃、箱体和流体部分进行了非结构化网格划分，球体和其他区域空间步长分别为5 和1 mm。瓦楞纸箱及衬垫壁面与果实之间要保持一定空隙以实现各计算域的连通性[26]。4 种开孔数包装预冷模型总网格单元数量约为6.9×106，网格质量检测表明这4 种模型的网格质量良好，整体偏斜度均低于0.9。

1.2.2 数值模型

1）控制方程

湿冷空气自由流动区域：采用雷诺平均数纳维-斯托克斯方程对不可压缩流体且瞬态自由气流区域进行求解。

连续方程：

式中Pps为蜜桃表面水蒸气压，Pa，当Pa>Pps时mcon的计算公式如6 所示，否则，mcon为0。ka为空气膜传质系数，kg/(m2·s·Pa)。

2）初始和边界条件

初始条件：蜜桃采后均匀放置在开孔数2、4、6 和9且对应开孔直径为40、40、40 和20 mm 的包装箱内，并将1-1 号蜜桃所测量的初始温度作为模拟仿真时的初始果温，分别为22.3、25.3、25.9 和23.4 ℃。

边界条件：将箱体迎风面前500 mm 处设置为速度-入口边界条件，背风面1 500 mm 处设置为压力-外流边界条件。试验和模拟方案中，入口速率和湿冷空气温度分别设置为1.2 m/s 和2 ℃。

3）FLUENT 数值模拟方法

蜜桃表面、箱体内外壁面及衬垫表面都设置为零粗糙度的防滑壁条件，垂直于壁的速率分量为0，沿着计算域两侧的法向梯度也是如此。仿真时采用SSTk-ω湍流模型，将动量、能量、湍动能和扩散系数的离散格式均设置为二阶迎风格式，利用基于压力的分离求解器进行求解；压力速度耦合方法采用SIMPLE 算法，时间步长为20 s；连续性、动量和湍流的收敛准则设置为10-4，能量方程的收敛准则设置为10-6。各物质热物性参数见表1。

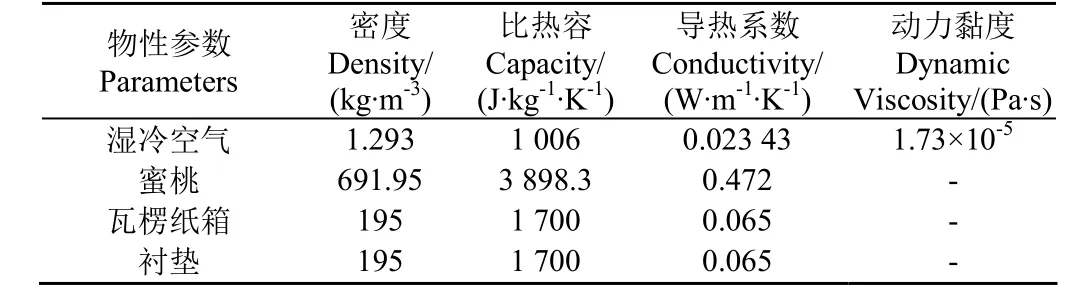
表1 蜜桃、空气和瓦楞纸箱、衬垫的热物性参数Table 1 Thermo-physical properties of peach, air, corrugated carton and tray

1.3 预冷效果评估参数

1.3.1 无量纲温度

归一化无量纲温度Y用于评估果蔬冷却速率，获得特定预冷时间。当Y=1/8 时，果实温度基本达到预期要求，所用时间称为7/8 冷却时间（Seven-Eight Cooling Time，SECT）。园艺果蔬预冷7/8 冷却时间后可将其转移至冷藏设备中消除剩余热负荷量，以降低预冷能耗成本[17]。因此，SECT 是用来比较冷却速率差异性的可靠参数。

式中Yi,t为i号果实在t时刻的瞬时Y值；Ti,p,t为i号果实在t时刻的内部温度，K；Ti,p,0为i号果实初始温度，K；Ta为空气温度，K。

1.3.2 整体预冷均匀性

与瞬时温度异质性指数相比[28]，本文整体异质性指数值（Overall Heterogeneity Index，OHI）可以直观判断整个预冷过程的均匀效果[29]。OHI 值越低代表果实在整个预冷过程中的温度分布越均匀，反之，果实温度分布均匀性越差。

式中m为所测果实个数；Yavg,t是t时刻所有果蔬无量纲温度Y的平均值；∆Yi,t为i号果实在t时刻冷却速率与整体平均冷却速率的差值，当∆Yi,t>0 时表示冷却速率超过整体平均冷却速率，为热点位置，反之，为冷点位置，∆Ymax-P或∆Ymin-N是∆Y的最大正数值或最小负数值。

2 构建GA-BPNN 预冷效果预测模型

2.1 建模流程

本文利用MATLAB 中Newff 函数初始化网络，网络模型训练函数为trainlm，隐含层和输出层神经元的传递函数分别为tansig 和purelin，遗传算法进化过程中迭代次数50，交叉概率0.4，变异概率0.01。GA-BPNN 预冷效果预测模型以送风速率、预冷空气温度、果实初始温度、箱体开孔直径和开孔数为输入因素，以SECT 和OHI为输出因素，其构建流程见图3[30-31]。

2.2 获取样本数据

利用SPSS 软件对影响蜜桃预冷的关键因素（送风速率0.5～2.5 m/s、预冷空气温度0～8 ℃、果实初始温度20～32 ℃和开孔直径20～40 mm）进行正交试验设计（见表2）以得到每种开孔数包装的25 种不同预冷工况条件，然后将其应用于这4 种不同开孔数中以获取100 组CFD-WIHS 模拟仿真数据，并根据公式（7）～（10）得到其预冷效果值，如表3 所示。

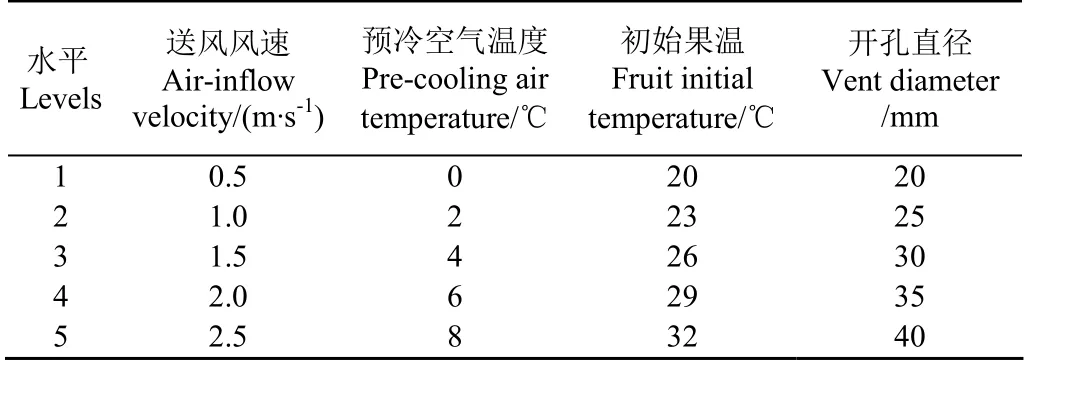
表2 预冷试验因素水平表Table 2 Precooling test factor level table

表3 不同开孔参数和预冷工况条件下单箱蜜桃的7/8 冷却时间SECT 和整体预冷均匀度OHITable 3 The seven-eight cooling time and overall uniformity of the peach at different opening parameter and precooling conditions

2.3 选取网络参数

通过公式（11）可知隐含层节点数B的优选范围为4～12[32]，并将B从4 调整到12 来进行网络训练，以分析SECT 和OHI 预测模型的均方根误差（Root Mean Square Error, RMSE）和平均绝对百分比误差（Mean Absolute Percentage Error, MAPE）[17]，由表4 可知B=4的预冷性能预测效果较佳。

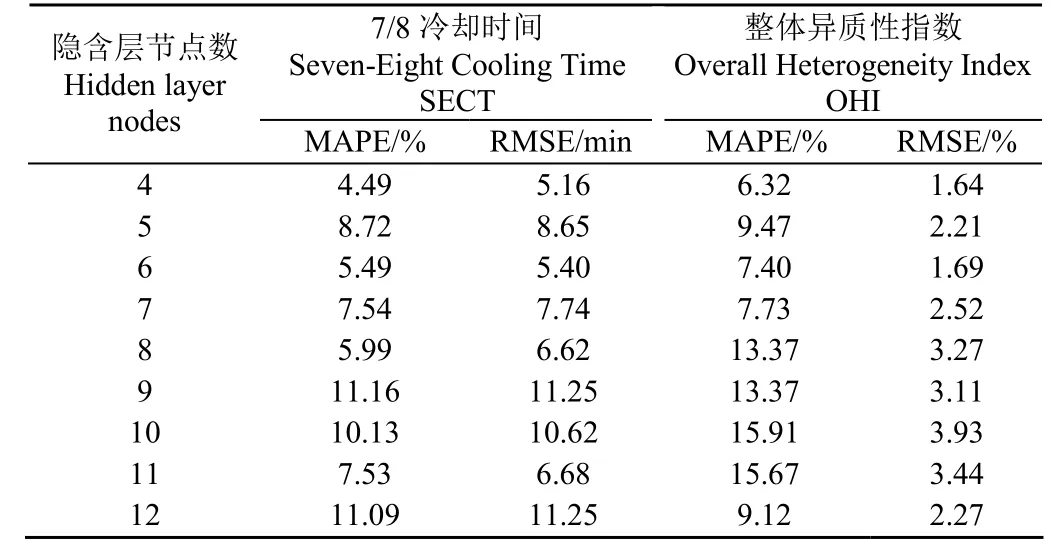
表4 通过网络训练优化选择最佳隐含节点数Table 4 Though the network training for getting the optimal selection of hidden nodes

式中N和M分别为输入层和输出层神经元个数，A为1～10 之间的常数。

为确定合适的种群规模，本文对20～100[33]内的种群规模数目进行了多次测试，发现当B=4 时，种群规模为30 或80 或90 所对应的RMSE 和MAPE 值较小（见表5），但由于种群规模越大代表同时处理的数据会更多，致使该算法运行时间得到了延长，因此，种群规模取30 较合适。

表5 遗传算法参数中种群规模的优化选择Table 5 Optimal selection of population size in genetic algorithm parameter settings

3 结果与分析

3.1 CFD-WIHS 传热传质数值模型的验证分析

本文计算了4 种不同开孔数包装箱内1-1 号蜜桃在预冷75 min 内果温和SECT 的误差值，其中测量值与CFD-WIHS 预冷模型的果温预测值间的最大RMSE 和MAPE 值分别为1.668 ℃和13.65%，而SECT 的最大相对误差值（Relative Error，RE）为19.23%，见表6。数据显示单箱三层蜜桃CFD-WIHS 传热传质数值模型在不同开孔参数下预测果温的RMSE 值均低于2 ℃，而SECT的最大RE 值均低于20%。这与前人构建的CFD 数值模型预测果温误差值相差不大[8-9,12,15,17,22]，如Han 等[15]所构建的单箱多层装苹果CFD 数值模型与实测果温间的最大MAPE 值为18.69%，朱文颖等[8]所构建包含隔板的单箱一层装苹果CFD 数值模型与实测果温间的最大RMSE 和ARD 值（Average Relative Deviation，平均相对误差）分别为1.73 ℃和13.80%。由图4 可知，不同开孔参数下利用CFD-WIHS 数值模型所预测的果温与实测温度变化趋势基本一致且两者结果基本吻合，其中开孔数为9 时整体预测误差较小，RMSE 值为0.819 ℃，MAPE 值为7.91%。

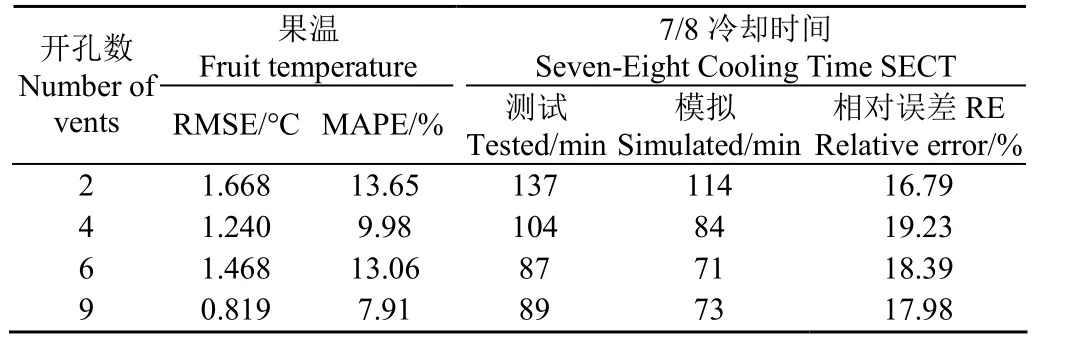
表6 不同开孔参数下果温和SECT 的模拟与试验数据Table 6 Simulated and tested data of fruit temperature and seven-eight cooling time on different opening parameters

综上可判断，CFD-WIHS 建模方法可用于预测不同开孔参数下单箱三层蜜桃的强制对流换热过程，这保障了后续预冷效果模型构建中样本数据的有效性及其预测精度。存在偏差的主要原因为：蜜桃建模时理想为等体积球体且无核，与试验中大久保蜜桃的形状存在差异；其次是预冷箱内风道系统出现内部空气与外部温暖空气对流换热及湿冷空气渗透至预冷设备外部的现象，导致预冷空气从通风孔进入箱内的温度存在波动。

当开孔直径在20～40 mm 时，不同预冷工况条件下开孔数6 和9 的OHI 值大部分低于其他开孔数模型（见表3），并在相同预冷环境下实测SECT 值较开孔数4 分别少了17和15 min，较开孔数2 少了50 和48 min（见表6）。由此发现，开孔数为6 和9 时更适合蜜桃快速均匀预冷，主要原因是各层通风孔的均匀分布可减缓上下两层之间的湍流干扰，使冷空气能通过衬垫与箱体间隙均匀流动。但开孔数6 和9 的预冷效果相差较小，因此，考虑包装箱的机械搬运强度，本文建议当开孔直径范围为20～40 mm 时，单箱三层果实采后预冷的较佳开孔数为6。

3.2 预冷效果预测模型误差分析

在100 组样本数据中，随机选择20 组作为测试集，80 组作为BP 神经网络训练集，网络学习样本数据先归一化，再经多次迭代，使试验数据的网络训练误差值逐步收敛。本文利用GA-BP 和BP 神经网络这两种算法对单箱三层蜜桃的SECT 和OHI 进行测试以获取较佳结果。结合图5 和表7 发现，这2 种算法对SECT 和OHI 的预测与实测值具有良好的拟合相关度，其中GA-BPNN 的决定系数R2值分别为0.962 5 和0.863 8，BP 神经网络的决定系数R2值分别为0.925 3 和0.815 9。这两种算法预测SECT 的决定系数R2值均高于0.90（见表7）。由此发现，这2 种算法预测SECT 时更为准确，这可能是由于整体预冷均匀度OHI 值的数量级较小，受到归一化与反归一化过程对测试和预测数据的“磨损”现象影响较为严重。

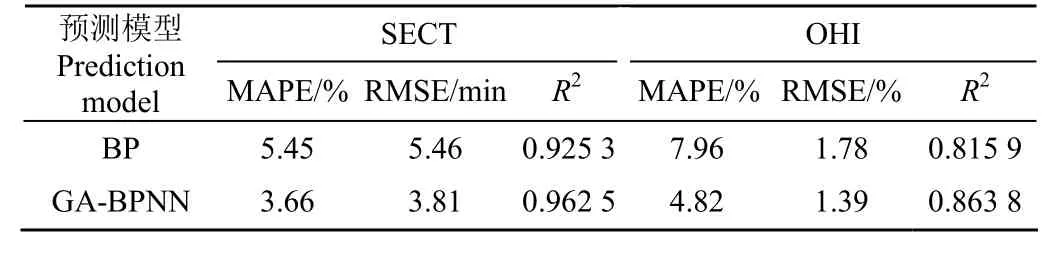
表7 对比分析各预测模型的MAPE、RMSE 和R2 值Table 7 Compare and analyze the mean absolute percentage error,root mean square error and decisive coefficient values of each prediction model

由图6 发现，利用GA-BPNN 预测SECT 时各测试样本的RE 值均低于10%，且预测OHI 时，其误差超出10%以上的样本数量少于BP 模型。利用GA-BPNN 预测SECT和OHI 时相对应的RMSE 值分别为3.81 min 和1.39%，其MAPE 值分别为3.66%和4.82%，与BP 神经网络模型相比，基于GA-BPNN 预测SECT 和OHI 时的RMSE 值分别低了30.22%和21.91%，其对应的MAPE 值也降低了32.84%和39.45%。这是因为GA-BPNN 算法可显著提高样本的适应度值，使样本数据的离散度明显变小以获取BP 网络各层之间最佳的权阈值。因此，GA 遗传算法的优化有利于避免BP 神经网络全面寻优时陷入局部极小值，从而能在较短时间内达到预定误差[34]，可应用于实现蜜桃预冷策略的智能化决策选择，及时预估不同预冷工况条件下的预冷效果。

4 结 论

1）建立了箱内含有衬垫层和果实内部热源项的计算流体热力学(Computational Fluid Dynamics-With Internal Heat Source，CFD-WIHS)传热传质数值模型，并试验验证了该建模方法的可行性和通用性，测量与模拟果温的最大均方根误差（Root Mean Square Error，RMSE）和平均绝对百分比误差（Mean Absolute Percentage Error，MAPE）分别为1.668 ℃和13.65%，预测7/8 冷却时间（Seven-Eight Cooling Time，SECT）的最大相对误差（Relative Error，RE）为19.23%，并发现开孔直径为20～40 mm 时适合单箱三层果实预冷的较佳开孔数为6。

2）遗传算法优化反向传播神经网络（Genetic Algorithm-Back Propagation Neural Network，GA-BPNN）采后蜜桃SECT 和OHI 预测模型的RMSE 和MAPE 值较BP 模型分别低了30.22%、32.84%以及21.91%、39.45%，这表明GA-BPNN 比BP 神经网络具有更高的预测精度，更能有效预估果实采后预冷效果。

3）构建了以送风风速（0.5～2.5 m/s）、预冷空气温度（0～8 ℃）、蜜桃初始温度（20～32 ℃）、开孔直径（20～40 mm）及开孔数（2、4、6 和9）为输入因素，以SECT 和OHI 为输出因素的采后蜜桃预冷效果预测平台，该平台可作为采后蜜桃在线监控预冷均匀性和冷藏转移时间以便于果实快速流入市场销售和降低预冷成本、提高果实预冷效果的新方法，也为中小型果园商业开发球类果实智能化预冷决策监控系统提供了理论参考依据。