基于PCA与K-Means的注射成形制品质量在线检测

黄佳文 孙瑞 阮宇飞

（上饶师范学院 江西省上饶市 334000）

注射成形是高分子材料的主要加工方法，注射成形可以一次性成形形状复杂、尺寸精确的高分子产品，此外注射成形还具有成形周期短、生产效率高等优点，因此注射成形在高分子成形领域得到了越来越广泛的应用[1]。作为一个典型的批次成形过程[2]，注射成形制品质量的一致性是评价最终制品质量的关键[3]。而在实际的成形过程中，由于环境的改变，机器参数的变化，材料的变化等，不可避免的会导致成形制品的质量发生波动[4]。随着注射成形工艺越来越广泛的应用，尤其是在成形制品向精密化、微型化发展的过程中[5]，对注射成形生产过程中波动的监测及成形制品质量的一致性提出了更高的要求。

为了提升注射成形精度，现有方法主要分为两大类。一类是从硬件提升的角度入手，比如采用精度更高的注射机，在注射机上或者模具内安装高精度的温度、压力传感设备[6]，监测成形过程的相关参数，从而实现对成形过程中的波动监控。此类方法可以有效地抑制成形过程波动，提高成形产品的精度，但这类方法存在着以下几个问题。首先是成形的成本会显著提高，如模内型腔压力传感器通常单价都在万元以上，而一套模具通常需要安装多个传感器，再加上配套的数据采集分析设备，导致成本显著增加。另外这一类传感器的安装通常是有损的，而有损的安装方法不可避免的会对成形设备及成形产品的质量产生一定的影响[7]。

另一类是基于注射成形过程数据的方法，注射成形过程是一个典型的批次过程，在成形过程中会产生大量的批次数据，使得基于数据的方法十分适用于注射成形领域[8]。如zhou 等人提出通过注射过程的压力数据，建立压力积分模型，实现对注射成形过程中的监控，并实现质量稳定性动态控制[9]。除了上述基于数据的机理模型方法，近些年来随着人工智能技术的快速发展，各类基于数据的人工智能技术在注射成形监控领域也得到了广泛的应用[10]。上述基于数据的方法在针对各自特定问题上都能取得较好的效果，但存在着成本高的问题。

针对现有技术存在的上述问题，本文提出了一种基于主成分分析（Principal Component Analysis, PCA）和K-means 聚类的注射成形质量检测方法。所提方法首先需通过注射机内置的料筒压力传感器采集注射过程中的压力数据，而不需要安装额外的传感器采集数据。采集到原始数据之后，先对数据进行预处理，然后将预处理之后的高维数据采用PCA 进行降维处理，得到设定维度的低维特征，并对得到的低维特征进行归一化（Normalization）处理，再将归一化处理之后的低维数据采用K-means 聚类算法进行聚类，再根据低维数据距离聚类中心的距离，判断当前批次的成形过程是否发生异常，从而实现对注射成形过程的在线监测。通过典型零件的成形实验表明，本文所提方法能够有效实现对注射成形过程的监测，显著提升成形制品质量的一致性，且所提方法不需要额外安装传感器，对样本的数据需要量低，对计算机的硬件要求低，能够实现低成本的有效监测。

1 数据采集与预处理

本文所提方法通过注射机料筒内置的压力传感器采集压力数据作为原始输入数据，通过信号线从注射机中的IO 接口中接出原始的模拟信号，采集得到连续的电压信号数据，在电脑端接收到采集的数据后，首先需要将采集的电压信号按对应的规则转换成实际的压力数据，得到料筒内的压力原始数据。采集得到压力原始数据存在着长度不统一，数据未对齐等问题，同时在采集过程中不可避免的会存在采集噪声，尤其是在采集片段的初始阶段，数据会存在着较大的波动。因此在进行下一步的PCA 处理前，需要对采集的原始压力数据进行预处理。在本文中首先采用滑动平均滤波法，具体如公式（1）所示：

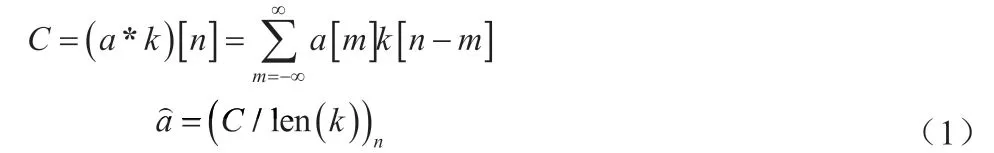
其中向量α表示原始采集的压力数据，长度为n，向量k 表示一维卷积核，在本文中取值全为1 向量k=[1,1,1,…,1]，C 表示原始数据序列与卷积核的离散卷积，len(k)表示卷积核的长度， 表示平滑后的压力数据，取离散卷积的中间值，其长度与原始数据长度保持一致。

压力数据平滑后，进一步的需要对数据进行清洗，保证每个批次的压力数据长度相等，且每个批次的数据是对齐的。在本文中数据清洗如公式（2）所示，首先通过选取注射压力曲线中第一个波峰的位置作为标记点s，分别向前取n 个数据，向后取m 个数据，从而得到每个批次长度统一为n+m+1 的压力数据序列，且每个序列对齐的压力数据。

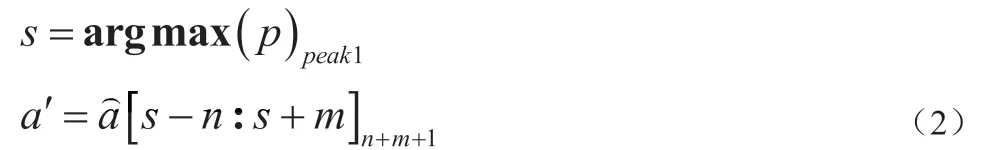
2 PCA降维与归一化

2.1 PCA降维

原始压力数据经过预处理之后得到长度相同且对齐的数据下一步需要对高维的数据进行特征提取，本文提出一种改进的基于PCA的降维方法，实现对高维数据的降维，从而实现对注射成形过程中的异常监测。PCA 的思想是将高维的特征映射到低维的空间上，假设原始数据的维度为m，所映射空间的维度为k，其中k＜m，k 维特征空间为全新的正交特征，在本文中设预处理之后的注射压力数据如公式（3）所示：

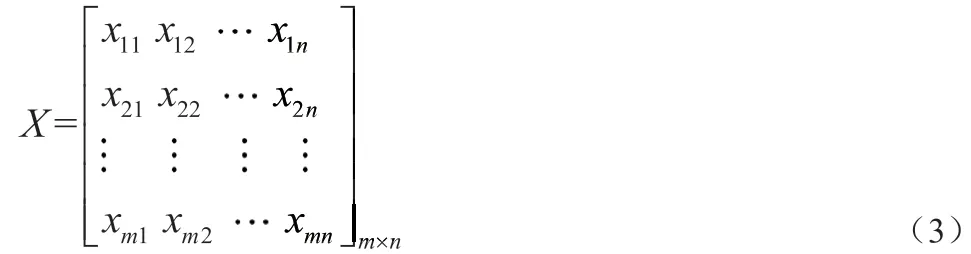
其中m 表示一个采样批次中压力数据的长度，n 表示采样数，对X 的协方差矩阵∑进行奇异值分解可以得到：

2.2 数据归一化

原始的高维压力数据经过上述PCA 降维之后，得到低维特征数据Y∈Rk×n，即每个采样批次数据维度从m 降低到k。在得到的降维数据中，通常会遇到每个维度的数据分布范围变化过大的问题，过大的数据分布范围对后续的聚类分析、异常批次的分类都会带来不利影响。针对上述问题，本文提出采用Min-Max Normalization的算法对降维后的特征数据进行归一化处理，具体公式如下所示：

其中A 表示降维之后某一个维度的特征数据， 表示当前维度中的最小数据， 表示当前维度中的最大数据，表示归一化之后的数据。

3 K-Means聚类分类

经前述处理得到归一化低维特征数据后，进一步需要对m 个模次的低维特征数据进行聚类分析及分类处理，本文提出采用基于K-Means 算法的无监督聚类算法，该方法实现相对简单，对计算机的性能要求较低，同时能够取得较满意的结果。

在K-Means 算法中，对于给定的样本，首先随机初始化质心，并计算每一个样本与质心之间的距离，将样本点归到距离最近的簇中，再重新计算每个类的质心，重复此过程，直到质心不再改变，并最终确定每个簇类的质心。上述过程的目标函数可用如下公式描述：

其中x 为样本点，μi为簇Ci的质心，算法的目标即为最小化平方误差L。

在传统的K-Means 算法中，每一轮迭代都需要计算所有样本点要质心的距离，当样本量很大时，算法的收敛速度会显著变慢。另一方面，如果所有的质心完全随机初始化的话，也会导致算法的收敛速度很慢。针对上述两个问题，本文分别提出了解决方案。首先针对质心的初始化问题，本文提出了一种新的质心初始化策略，具体流程如下：

（2）对样本中的每一个点xj计算其与已选择的质心中最近的质心距离

（3）根据d(xj)的大小，选择一个新的质心，d(xj)越大，被选为质心的概率则越大；

（4）重复步骤（2）和（3），直到选择出所需的质心；

针对传统K-Means 算法中每一次迭代都需计算所有样本点到质心，从而导致收敛速度慢的问题，本文采用了距离计算优化的Elkan K-Means 计算方法，以减少不必要的距离计算，其主要包含了以下两种计算策略：

（5）对于某一个样本点x 和两个质心μi1、μi2，假设已知两个质心的距离为如果计算发现即根据三角形两边之和大于第三条边，则可知，因此就不需再计算的值；

（6）对于某一个样本点 和两个质心μi1、μi2，根据三角形的性质可知，

利用上述两个计算策略在K-Means 算法迭代过程中，可以有效减少计算量，加快算法的收敛速度，为所提方法在注射成形质量在线检测的可行性提供了保证。

4 实验验证

4.1 实验设计

为了验证本文所提方法的有效性，本文设计了多个实验，从多个角度验证本文所提方法的有效性。实验所用注射机为JSW 公司生产的J110ADC-180H 型注射机，实验所用模具为一模两腔的透镜模具，产品的CAD 模型如图1(a)所示，成形产品实物图如图1(b)所示。由于成形产品需要具备较高的透明度，实验所用材料为聚碳酸酯（PC），为了保证最终成形产品质量，并尽可能地排除外界的因素对实验结果的影响， 成形前需进行烘料处理，在120℃下烘料3 小时。

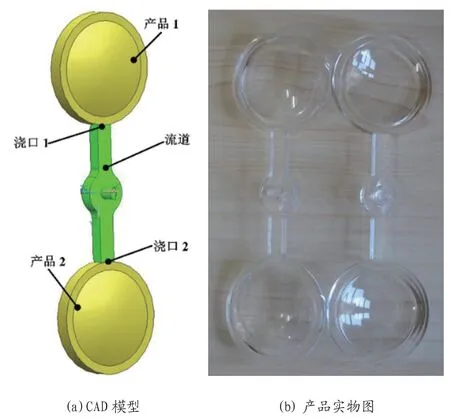
图1：实验注射成形产品

实验过程中，通过注射机内置Minebea 压力传感器实时采集注射过程中每个批次的注射压力，并通过数据采集卡采集传感器的信号，注射压力信号的采样频率为1000Hz。实验过程中相关工艺参数的设置如

表1所示。本文实验中通过采用产品的重量来反应产品质量的异常情况，研究表明产品的重量可以很好地反映成形过程的稳定性和产品的一致性，而且产品重量与产品其他的质量特性密切相关[11]。因此采用产品重量可以很好地表征成形产品的一致性，而且相对于其他的产品质量评价指标，产品的重量可以十分方便的测量及量化表示。

4.2 实验结果与讨论

如图2所示为连续10 个模次的注射压力曲线，注射过程中注射速度分为三段，首先熔体以较快的速度经过流道，然后再以较慢的速度经过浇口，而后再以稳定的速度填充型腔，直到最后进入熔体压缩阶段，整个注射过程时间约为 2330ms。从图中可以看到在原始的压力数据中存在着大量的噪声信号，尤其是在信号采集的初始阶段，同时在原始数据中存在着数据未对齐的情况，而噪声和未对齐的数据，会影响后续的数据分析，掩盖数据中的有效特征，使得后续的特征提取操作中提取出错误的特征，并最终导致错误的质量检测结果。

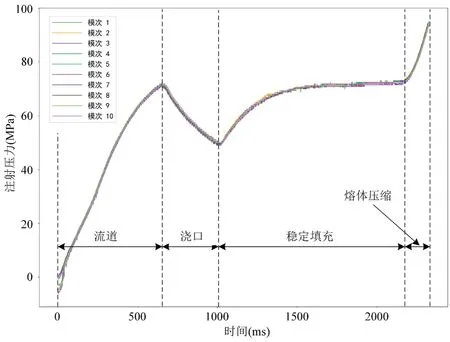
图2：注射压力曲线

为了降低原始数据中的噪声及数据未对齐对检测的结果的影响，本文中通过对原始的压力数据进行预处理，首先采用滑动平均滤波法对原始数据进行滤波以减少原始数据中的噪声，在此基础上再以第一段数据的峰值点为参考点，对数据进行对齐。如图3所示为预处理之后的注射压力曲线，可以看到相对于原始的注射压力数据，经预处理之后的压力数据噪声信号显著降低，且不同采样周期的数据的对齐度也有较大的提升。

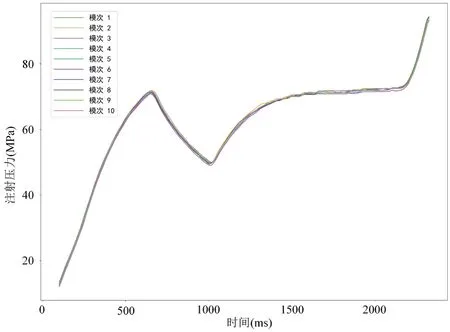
图3：预处理后注射压力曲线

经过上述预处理之后，进一步采用本文所提的PCA 降维方法对预处理后的高维数据进行降维，以提取低维特征数据。在本文中设定提取的低维特征数据的维度为3，该维度可根据情况任意设定。提取得到低维特征数据后，进一步地对低维特征数据进行归一化处理后，即可得到低维特征数据分布，但该低维数据依旧无法直接分类。

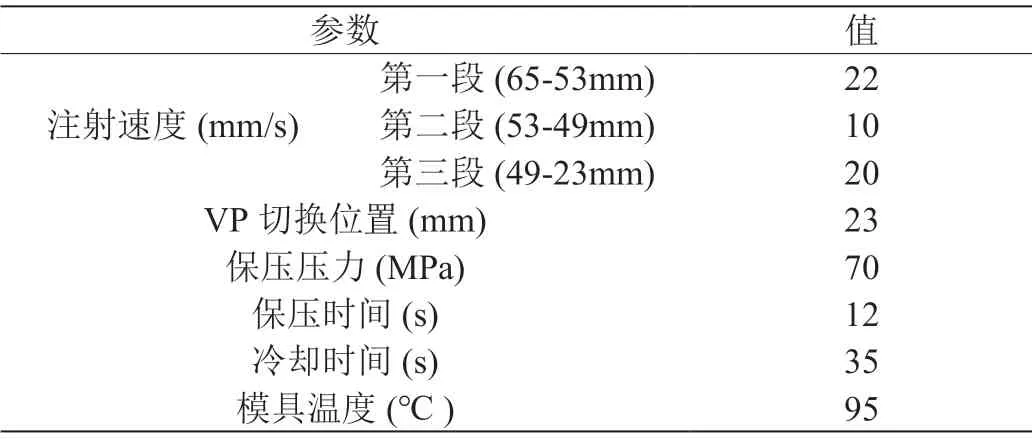
表1：工艺参数设置

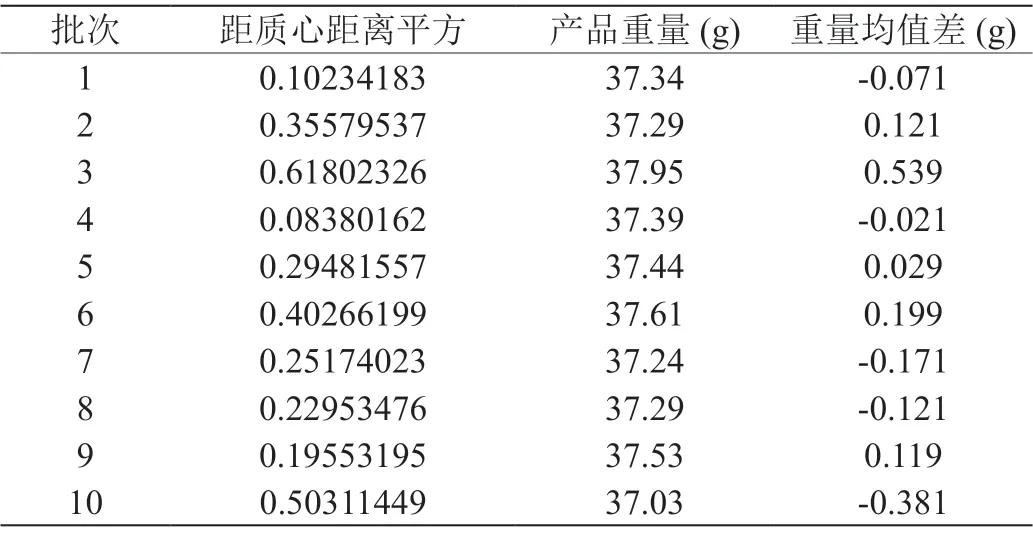
表2：低维特征分布与重量结果统计

在前述PCA 降维之后，本文提出采用改进后的K-Means 算法对低维特征数据进行聚类，再根据样本与聚类中心的距离判断当前批次是否发生异常。如图4所示为对低维特征数据进行聚类之后的分类情况，其中聚类的质心数为1，其中红色的点为聚类质心，以聚类质心为中心，半径r=0.66 画一个球，可得到如图中所示的绿色虚线球体。从图中可以看到，第3 个批次及第10 个批次的样本分布在球体外侧，这表明这两个批次成形过程中很有可能发生了异常，成形产品的质量也很可能发生了波动。

图4：低维特征数据分类

进一步地为了验证上述10 个批次成形产品的质量情况，分别对每个批次的产品进行称重，并计算每个批次低维特征数据点距离聚类质心的距离，可以得到如表2所示的统计数据。从表中可以看到批次3 和批次10 的低维特征数据距离聚类质心距离的平方要显著高于其他批次，尤其是第3 个批次，其低维特征维度所在的空间坐标距离聚类质心的距离平方已经超过了0.6，类似的第10 个批次的也超过了0.5，而其他批次低维特征点距质心距离平方基本都在0.4 以内。从每个批次产品的重量可以看到，第3 批次和第10 批次产品的重量发生了显著的波动，其重量与均值重量差分别为0.539g和-0.381g，而其他批次的重量偏差都在±0.2g 以内。这表明降维得到的低维特征数据的分布，可以很好地表征当前批次成形产品质量的情况，当某个批次成形过程中发生波动，通过本文所提方法可以有效地在线检测出，从而提高注射成形产品质量的一致性。

5 结束语

本文提出了一种基于PCA 降维与K-Means 聚类的注射成形制品质量在线检测方法，所提方法首先通过PCA 算法对预处理后的注射过程压力数据进行特征提取，得到低维特征数据，并对所得低维特征数据进行归一化处理。进一步地，通过采用K-Means 算法对低维特征数据进行聚类处理，找出低维特征数据中发生异常离群的采样点，从而实现对成形过程中质量波动的检测。根据实验结果可以得到如下结论：

（1）采用PCA 方法从注射过程中高维压力数据中特征提取得到低维特征数据，可以很好地表征成形产品的质量。

（2）采用K-Means 算法对所提取的低维特征数据进行聚类处理，可以有效区分正常批次与异常批次，实现对注射成形过程的异常检测与分类。

（3）相较于其他注射成形质量检测方法，本文所提方法不需要安装额外的传感器，可以低成本的实现注射成形过程质量在线检测。