超级电容储能系统鲁棒分数阶PID控制设计

李敬航，赖伟坚，陈威洪，李敬光，杨德玲，余涛

(1.广东电网有限责任公司东莞供电局，广东省东莞市 523000；2.苏州华天国科电力科技有限公司，江苏省苏州市 215000)

0 引 言

随着我国电网规模的持续扩大，电力系统负荷不断升高，光伏、风电等可再生能源接入已成为必然趋势[1]。然而，大规模的可再生能源接入势必会对区域配电网造成不利影响，给电网的安全稳定运行带来极大挑战[2-3]。储能技术的提出有效弥补了可再生能源并网的缺陷，对促进可再生能源消纳，改善电能质量，提高电力系统运行稳定性具有重要意义[4-5]。

近年来，超级电容储能系统(supercapacitor energy storage system, SCES)以其高效率、低污染、免维护、快速充放电和循环使用寿命长等优异特性受到了人们的广泛关注[6]。电压源型换流器(voltage source converter, VSC)作为SCES最常用的模块之一，具有较强的时变非线性。如果负载是电阻等非线性负载或者冲击性负载，则电路的非线性特性将会进一步增强[7]。因此，如何设计合理的VSC控制系统是保证SCES稳定运行的关键。传统的线性控制方法，如PID控制，虽然结构简单，可靠性高，但其控制增益是通过局部线性化来选择的，不能保持全局一致的控制性能。当系统运行点随着环境剧烈变化而发生较大范围的频繁偏移时，其控制性能将不可避免地下降，严重时将导致电力系统失稳[8]。

为了解决这一问题，人们提出了大量非线性控制策略。文献[9]针对智能配电系统和微电网中具有分布式能源的SCES，设计了一种反馈线性化控制策略，完全消除了SCES的非线性。文献[10]采用了一种基于互连和阻尼分配的无源控制(interconnection and damping assignment passivity-based control, IDA-PBC)策略，利用其物理特性显著增强了SCES的动态响应。文献[11]针对SCES提出了一种滑模控制策略，不仅提高了充电效率，显著延长了储能设备的循环使用寿命，而且还使系统具有更快的启动响应能力和更强的鲁棒性。文献[12]提出了一种基于模糊算法的SCES优化控制策略，不仅能在保持直流母线电压稳定的同时提高储能系统的功率输出能力，而且能有效改善传统算法控制中产生的系统振荡，优化蓄电池的工作过程从而延长其寿命。文献[13]针对蓄电池/超级电容混合储能系统提出了一种模糊滑模控制策略，采用模糊控制器消除滑模控制器的高频抖振现象，有效提高了系统的抗扰性能。文献[14]针对蓄电池/超级电容混合储能的独立光伏发电供电系统设计了一种非线性控制策略，通过对双管双向变流器的控制，有效稳定了供电系统的输出电压，显著提高了光伏发电系统的供电能力。

然而，上述控制器通常需要对多个参数进行整定且结构较为复杂，难以在实际工程中获得应用。本文针对配电网中的SCES设计一款新型鲁棒分数阶PID(robust fractional-order PID control, RFOPID)控制，并将其与传统PID控制[8]和IDA-PBC[10]在3种算例下进行对比，以验证RFOPID控制的有效性和鲁棒性。

1 SCES建模

为建立合理的SCES控制模型，作出以下2个假设：1)忽略VSC自身电压降；2)忽略VSC产生的谐波功率。图1给出了SCES的并网结构示意图。其数学模型描述如下[10,15]：

图1 SCES并网结构示意图

(1)

(2)

(3)

式中：LT和RT分别表示变压器的电感和电阻；id和iq是流经变压器的dq轴电流；ω是交流电网频率；md和mq是dq轴调制指数，为避免VSC的过调制，其取值范围为[-1,1]；Ed和Eq分别表示交流电网的dq轴电压；Csc是超级电容的电容值；Vdc表示超级电容的输出电压。

有功功率Pac和无功功率Qac计算如下：

Pac=Edid+Eqiq

(4)

Qac=Eqid-Ediq

(5)

2 SCES的RFOPID控制设计

2.1 SCES储能特性分析

VSC交流侧和直流侧之间的功率传输由超级电容的总存储能量决定，如式(3)所示。直流电压Vdc取决于dq轴电流id和iq。定义储能变量z(t)=CscVdc，由此可以计算出z(t)的动态响应，如下所示：

(6)

式中：z0为储能变量z(t)的初始值；s(τ)为VSC交流侧和直流侧之间传输的有功功率；Lsc为超级电容系统的电感。

SCES的能量存储特性如图2所示，图中存在2个临界点A和C，分别表示SCES可容许的最小能量值和最大能量值。通常，SCES运行在A点和C点之间，记为B点。B点的有功功率参考值记为P，SCES的能量存储特性如下：

1)若P为正，则SCES储存的能量将沿图2中绿色轨迹从B点下降到A点；

2)若P为负，则SCES储存的能量将沿图2中绿色轨迹从B点升高到C点；

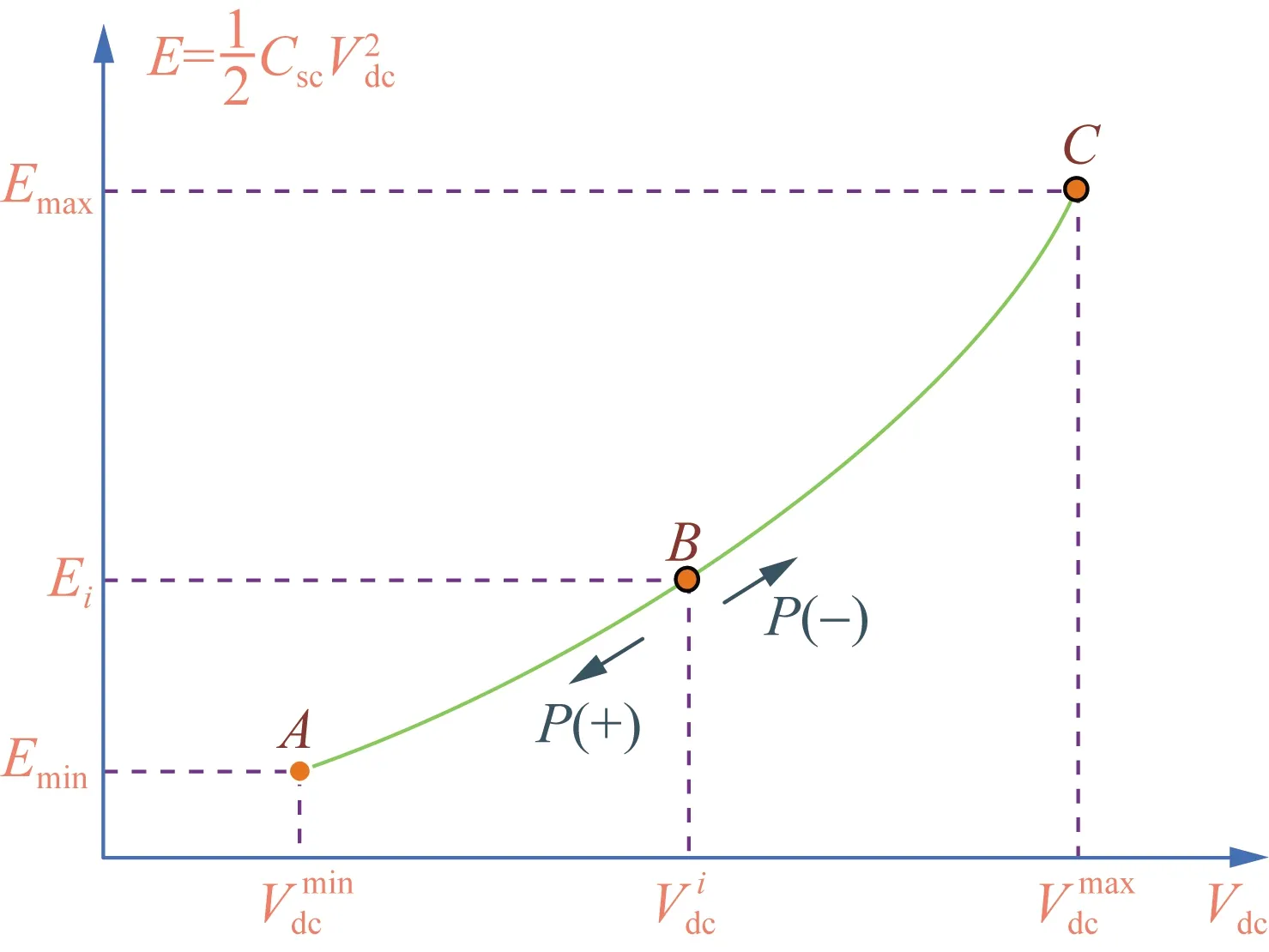
图2 SCES的能量存储特性曲线

3)为了增加(或保持)SCES储存的能量，A点的有功功率基准只能为负(或0)，C点则相反。

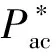
(7)

(8)

式中：β为SCES的运算系数，定义如下：

(9)

式中：zmin和zmax分别是储能变量z(t)的最小值和最大值。

2.2 RFOPID控制器设计

(10)

式(10)可由如下矩阵表示：

(11)

其中，

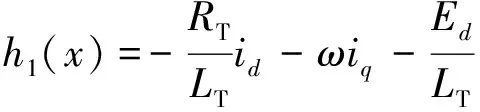
(12)

(13)

(14)

为实现式(11)的输入-输出线性化，控制增益矩阵B(x)在其运行范围内必须是可逆的[16-17]，即：

(15)

由于直流电压Vdc始终大于0(等于0表示SCES停止工作，失去可控性)，因此上述条件始终成立。

跟踪误差的扰动ψ1(·)和ψ2(·)定义如下：

(16)

其中，

(17)

至此，跟踪误差e与控制输入u之间的关系可改写如下：

(18)

应用高增益扰动观测器(high-gain perturbation observer, HGPO)估计扰动ψ1(·)和ψ2(·)[18-19]，得：

(19)

(20)

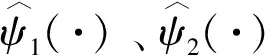
基于跟踪误差式(18)设计RFOPID控制，如下：

(21)

式中：KP1,KP2,KI1,KI2,KD1和KD2表示PID控制增益；λ1和λ2表示分数阶微分的阶数；μ1和μ2表示分数阶积分的阶数；s是复频域。

SCES的总体RFOPID控制结构如图3所示。因为RFOPID控制器不依赖于精确的SCES模型，仅需测量dq轴电流就能实现平滑地误差跟踪。

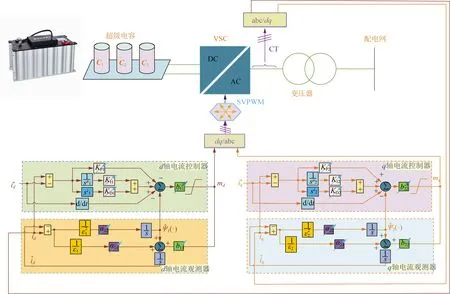
图3 SCES的总体RFOPID控制结构示意图

需要说明的是，本文选用HGPO对SCES的非线性、未建模动态和参数不确定性所聚合的扰动进行在线快速估计。其原因如下：1)HGPO结构简单，所需设计参数少；2)HGPO观测速率快，收敛迅速，稳定性较高。但当观测信号不连续时(如出现阶跃扰动)，系统将会出现瞬时Peaking现象，短时间内观测误差将迅速增大，通常采用观测器限幅来减少该影响。

3 算例分析

SCES并网的拓扑结构如图4所示，风能和太阳能等新能源发电系统经母线1接入配电网中。SCES参数及配电网参数详见文献[9]。本节将所提出的RFOPID控制与传统PID控制[8]和IDA-PBC[10]，在3种算例下进行误差跟踪性能和鲁棒性比较：1)有功功率和无功功率调节；2)三相短路下的系统恢复；3)鲁棒性测试。其控制器的控制参数如表1所示。仿真采用Matlab/Simulink 2016a搭建。

表1 三种控制器的控制参数

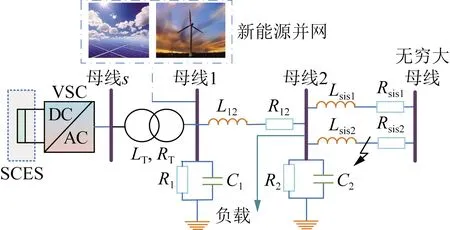
图4 新能源并网的SCES拓扑结构

3.1 有功功率和无功功率调节

SCES的主要目的是为所连接的电网提供电力支持，同时补偿非线性负载或故障引起的功率不平衡。本算例旨在评估不同运行条件下SCES调节有功功率和无功功率的能力。分别使用RFOPID控制、PID控制和IDA-PBC来跟踪系统的功率参考值，相应的系统响应如图5所示。由图5可见，RFOPID控制具有最佳的有功和无功调节性能。特别地，在第二次功率不平衡阶段，PID控制、IDA-PBC和RFOPID控制的有功功率收敛时间分别是0.22、0.26和0.10 s；在第三次功率不平衡阶段，PID控制、IDA-PBC和RFOPID控制的无功功率收敛时间分别是0.20、0.25和0.09 s。

图5 功率调节下的系统响应

3.2 三相短路下的系统恢复

电网故障会导致瞬时功率不平衡，产生功率振荡和电压跌落。SCES作为电网备用系统，必须在电网受到干扰后，为电网提供即时的有功功率和无功功率。本算例旨在评估故障条件下RFOPID控制的有效性。选取如下故障进行仿真分析，t=0.5 s时母线2与无穷大母线之间的一条输电线路发生三相短路，如图4所示。t=1.1 s时，自动重合闸装置启动。图6给出了该工况下的系统响应，可以看出，RFOPID控制可以有效地提高系统的故障恢复能力。特别地，在第一次故障恢复阶段，RFOPID控制的有功功率超调量分别是PID控制、IDA-PBC的43.53%、57.81%；在第二次故障恢复阶段，RFOPID控制的无功功率收敛时间分别是PID控制、IDA-PBC的26.51%、32.76%。

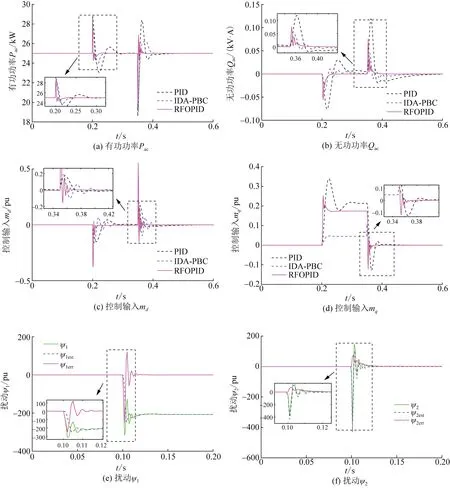
图6 系统发生三相短路下的系统响应

3.3 鲁棒性测试

本算例旨在测试电网参数不确定下RFOPID控制的鲁棒性。假设所研究的电网等效电阻Req和等效电感Leq在标称值附近±20%变化。当电网故障致使无穷大母线处出现30%的电压跌落时(持续时间约100 ms)，记录电网有功功率的峰值|Pac|。相应的系统响应如图7所示，可以看出，RFOPID控制在系统参数不确定下具有最强的鲁棒性。特别地，Req变化时，PID控制、IDA-PBC和RFOPID控制的|Pac|变化率分别为42.27%、39.86%和16.09%。

图7 电网参数不确定性下的系统响应

3.4 定量分析

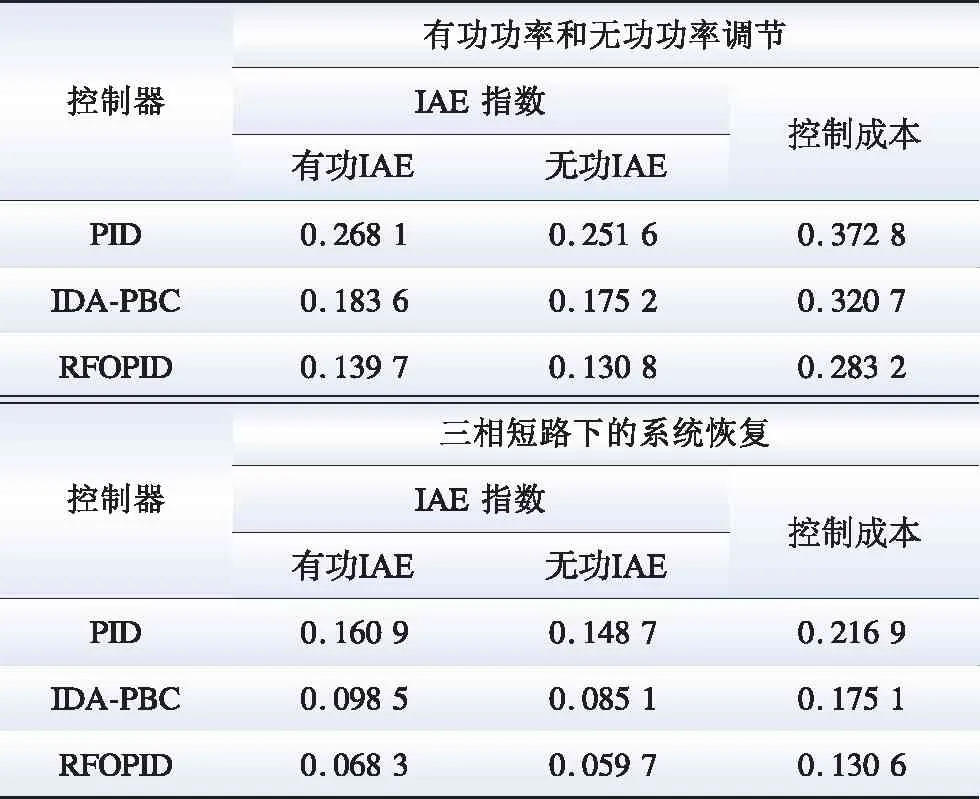
表2 各控制器2种工况下的IAE指数以及总体控制成本

4 结 论

本文针对SCES设计了一种RFOPID控制，主要贡献可归纳为如下3个方面：

1)基于HGPO对SCES的非线性、未建模动态和参数不确定性所聚合的扰动进行在线快速估计，并通过FOPID控制器对其进行完全补偿，从而获得全局一致的控制性能。

2)RFOPID控制不依赖于精确的SCES模型，只需测量dq轴电流，结构简单，易于硬件实现。此外，通过分数阶微分和积分使得系统的动态响应能力显著提高。

3)基于有功功率和无功功率调节、三相短路下的系统恢复和鲁棒性测试下的仿真结果表明，RFOPID控制较PID控制和IDA-PBC，在跟踪速率、跟踪误差和总体控制成本方面均具有显著优势。其有功功率的跟踪误差仅为PID控制和IDA-PBC控制的52.11%和76.09%；在三相短路下的系统恢复算例中，其总体控制成本仅为相应控制器的60.21%和74.58%。

在未来的研究中，将考虑把RFOPID控制运用到实际的SCES系统和实验室微电网中，以进一步研究其硬件实施可行性。