基于区域能源中心的居民电-热用能多目标优化
匡萃浙,张勇军,王群,邹舟诣奥
(1.深圳职业技术学院,广东省深圳市 518055;2.华南理工大学电力学院智慧能源工程技术研究中心,广州市 510640)
0 引 言
由于资源、气候和环境的多重压力,追求能源的高效利用、清洁环保和可持续发展是能源领域的发展趋势[1-2]。居民等建筑用能约占据总用能消费的40%,且随着经济发展,居民生活能耗逐年提高[3-4]。居民用能优化既可为用户节约成本,改善用户用能经济性,又可以促进能源结构转型发展,近年来受到了广泛关注。
文献[5]以天然气为替代能源,以用户经济性和满意度最好为优化目标,建立了居民用户用电优化模型。文献[6]以家庭用电费用最优、售电公司经济收益最大为目标,提出了家庭柔性负荷管理和售电公司售电决策协同优化模型。文献[7]从实际情况出发,提出了可行的家庭能量管理系统拓扑,并利用不需要提供预测信息的模糊控制方法来对系统的能流进行实时控制。文献[8]基于任务分类和基本经济规律,针对居民的偏好和需求,建立了新的用于居民用能优化的效用函数数学模型。上述研究均只考虑单一的用电优化,然而居民能源消费,涉及多种能量形式,典型的有电、热、气。
电、热、气等用能之间存在耦合性,不同能源之间可通过能源转换电器、能源转换设备转换替代。文献[9-10]在需求侧响应中考虑了电/热负荷需求响应和供需双侧热/电耦合,但研究的目标与居民用能优化无关。为了进一步提升居民的用能效益、降低其用能成本,对居民多种用能同时优化是十分必要的。当前在电能和热能消费方面,用户侧和供能侧能源转换设备应用成熟,而实现电-气能源转换的电转气设备还处于试点应用阶段,同时居民侧也不具备电气2种能源转换的条件。因此,考虑方法的实用性,本文聚焦于解决居民电-热2种用能优化问题。
区域能源中心(district energy centre,DEC)的发展与应用为优化居民电-热用能提供了新思路。DEC是连接上级能源网络和下级用户的枢纽站,以电能、天然气为能源输入端,集合各类能源转换器,可实现区域内电、热、冷、气等多能流之间的耦合优化分配[11-12]。这里的区域指的是以居民小区、办公楼宇为主的小规模用能区域。文献[13]考虑光伏发电/产热及储能设备,以居民能源购置成本为目标,构建了面向居民用户的DEC优化运行模型,但在该研究中居民用户的用能是作为固定的负荷曲线,居民用能电器没有参与优化。
而在居民侧,热水器和空调等能源转换电器将电、气能源转换成热能,其用能功率高,属于惯性负荷,可在短时间内迅速调整功率且对用户的舒适性影响较小[14-15],具有较强的功率调节潜力,广泛应用于居民用能优化和改善电力系统运行的需求侧响应中[16-18]。
综上所述,针对当前居民用能优化仅考虑单一电能的不足,本文首次提出居民侧能源转换电器和DEC协同运行方法。首先,提出耦合DEC的居民用能通用化建模方法;接着,以居民购能成本最小和用户不舒适性最小为目标,构建居民用能多目标优化模型,并基于模糊隶属度函数求解多目标最优折中解;最后,以某区域冬季居民用能优化为例开展算例验证。
1 耦合DEC的居民用能模型
耦合DEC的居民用能系统如图1所示。居民用户的用能包括电负荷和热负荷,其中居民内部的能源转换电器可将电能、天然气转换为热能。居民用户的电负荷和热负荷同时由DEC通过新能源、能源转换设备以及能源储存设备协调运行对上级能源系统多能流在区域级进行再次分配供应。居民用户的能源转换电器与DEC耦合协同运行可实现居民用户用能优化。
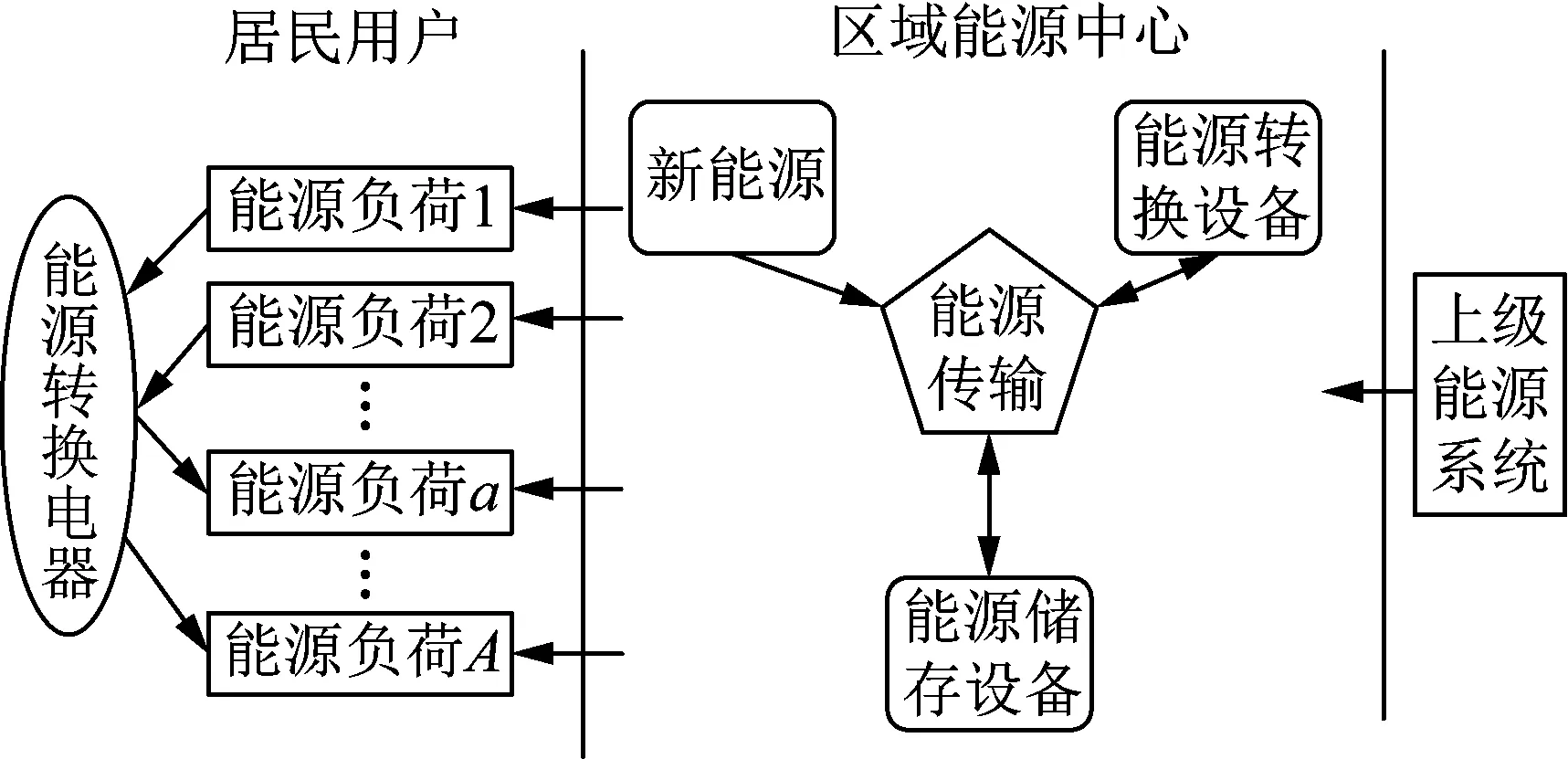
图1 耦合DEC的居民用能系统
在日前居民用能优化研究中,为反映耦合DEC的居民用能系统中多种能流稳态功率转换关系,可基于能源集线器模型对系统中多能流的输入输出及转换关系进行建模[19]。由能量守恒定律可知,系统中各处节点的输入能源需要和输出能源相等。在图1所示的居民用能系统中,存在3项能源平衡,分别为:
1)用户用能功率与DEC输出能源功率和能源转换电器输出能源功率之间的平衡;
2)DEC输出能源功率与能源转换设备和能源储存设备输出能源功率以及不流经能源转换设备能源功率之间的平衡;
3)从上级能源系统购入能源功率和可再生能源出力功率与能源转换设备和能源储存设备输入功率以及不流经能源转换设备能源功率之间的平衡。
由上述3项能源平衡,可构建能源功率平衡方程式(1)—(3),式(1)—(3)分别对应能源平衡项1)—3)。
LUR+EUI=LDU+EUO
(1)
LDU=EN+ES+EDIS
(2)
EC+EN+ECH=EBUY+EP
(3)
式中:LUR为居民除能源转换电器外的用能功率向量,LUR=[LUR,a]A×1,LUR,a表示用户的第a类用能功率,A表示用户的总用能类数;LDU表示DEC输出能源功率向量,LDU=[LDU,a]A×1,LDU,a表示DEC输出的第a类能源功率;EUI和EUO分别为能源转换电器总能源输入和输出功率向量,EUI=[EUI,b]B×1,EUO=[EUO,b]B×1,EUI,b和EUO,b分别表示能源转换电器输入和输出第b类能源功率,B表示能源转换电器输入和输出的能源总类数;EN表示不流经DEC能源转换设备的能源功率向量,EN=[EN,a]A×1,EN,a表示不流经DEC能源转换设备的第a类能源功率;ES表示DEC能源转换设备的总能源输出功率向量,ES=[ES,a]A×1,ES,a表示DEC能源转换设备输出的第a类能源功率;EDIS表示能源储存设备放能功率向量,EDIS=[EDIS,a]A×1,EDIS,a表示能源储存设备放出的第a类能源功率;EC为能源转换设备总能源输入向量,EC=[EC,a]A×1,EC,a表示DEC能源转换设备输入的第a类能源功率;ECH为能源储存设备的充能功率向量,ECH=[ECH,a]A×1,ECH,a表示能源储存设备充能消耗的第a类能源功率;EBUY为用户从上级能源系统购买的能源功率向量,EBUY=[EBUY,a]A×1,EBUY,a表示用户从上级能源系统购买的第a类能源功率;EP为用户的可再生能源出力功率向量,EP=[EP,a]A×1,EP,a表示用户的可再生能源对第a类能源的出力。
式(1)—(3)中的能源转换电器和能源转换设备的输入功率和输出功率之间存在能源转换关系[20],如下所示:
(4)
(5)
式中:Ein=[Ein,g]G1×1和Eout=[Eout,d]D1×1分别为能源转换设备的输入和输出功率向量,G1、D1分别为能源转换设备的输入和输出功率种类数;Euin=[Euin,g]G2×1和Euout=[Euout,d]D2×1分别为能源转换电器的输入和输出功率向量,G2、D2分别为能源转换电器的输入和输出功率种类数;NC1=[nC1,ag]A×G1和NUC1=[nUC1,ag]A×G2分别为能源转换设备和能源转换电器的输入关系矩阵,若Ein,g和Euin,g属于第a类能源,则nC1,ag和nUC1,ag为1,否则为0;NC2=[nC2,ad]A×D1和NUC2=[nUC2,ad]A×D2分别为能源转换设备和能源转换电器的输出关系矩阵,若Eout,d和Euout,d属于第a类能源,则nC2,ad和nUC2,ad为1,否则为0;B1=[B1,gd]G1×D1、B2=[B2,gd]G2×D2分别为能源转换设备和能源转换电器的能源转换关系矩阵,若Ein,g和Eout,d对应相同能源转换设备,则B1,gd为1,否则为0,若Euin,g和Euout,d对应相同能源转换电器,则B2,gd为1,否则为0。
将式(4)和式(5)代入式(1)—(3)中,并进行消元处理,可得到:
LUR=(NUC2B2-NUC1)Euin+EBUY+EP+
EDIS-ECH+(NC2B1-NC1)Ein
(6)
综上所述,耦合DEC的居民用能系统的数学模型可以用式(6)所示的能源功率平衡方程描述,该模型能量关系均为常系数线性方程,具有直观性、通用性和实用性。
2 居民用能多目标优化模型
2.1 优化模型
本文构建的居民用能多目标优化模型,其优化目标涉及居民购能费用最低和不舒适度最小。
1)居民购能成本最低。
(7)
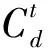
2)居民不舒适度最小。
本文利用空调和电热水器2种能源转换电器实现居民内部电能与热能转换。借鉴文献[9]研究成果,将居民室内供暖需求和热水需求转换为柔性热负荷:
(8)
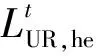
能源转换电器的用电功率受用户所需室内温度和热水温度的影响,设定弹性的室内温度和热水温度范围有利于能源转换电器参与居民用能优化,但温度波动将影响用户的舒适性。本文引入不舒适度指标ζ,ζ定义为室内/热水温度与用户设定的理想温度间距离的平方,该值越大说明实际温度与理想温度偏差越大,用户的舒适性越差,即:
(9)
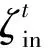
进一步,优化目标居民不舒适度最小描述如下:
(10)
2.2 约束条件
居民多目标用能优化模型约束条件包括居民用能功率平衡约束、居民能源转换电器运行约束、用户舒适度约束、能源转换和储存设备的运行约束。
1)居民用能功率平衡约束。居民用能功率平衡约束即为式(6),在调度周期内每个时段,均须满足式(6)的功率平衡。
2)居民能源转换电器运行约束。
(11)
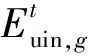
3)用户舒适度约束。用户的室内采暖和热水温度必须维持在用户设定的舒适区间内。
(12)
4)能源转换设备运行约束。能源转换设备运行约束包括运行功率上下限约束和设备爬坡约束。
(13)
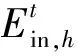
5)能源储存设备约束。能源储存设备运行受剩余容量和最大充放能功率的约束,而且同一时刻能源储存设备只能进行充能或放能,引入标志能源储存设备的充能状态和放能状态的0-1布尔变量,能源储存设备约束描述如下:
(14)
(15)
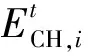
2.3 求解方法
2.1节构建了一个双目标混合整数二次规划模型,本文采用加权和法将上述双目标优化问题转化为单目标问题[21],设定等差目标权重数列,求解Pareto前沿,进一步基于模糊隶属度函数确定问题的最优折中解,具体如下:
步骤1:分别求解式(16)和式(17)所示的优化模型,得到目标函数f1和f2的最大值和最小值。
(16)
(17)
式(16)和式(17)所描述的优化模型分别为混合整数线性模型和混合整数二次规划模型,均可用CPLEX求解器求解。
步骤2:设置目标函数权重划分段数,基于加权和法将双目标优化问题转化为单目标问题,求解Pareto前沿。
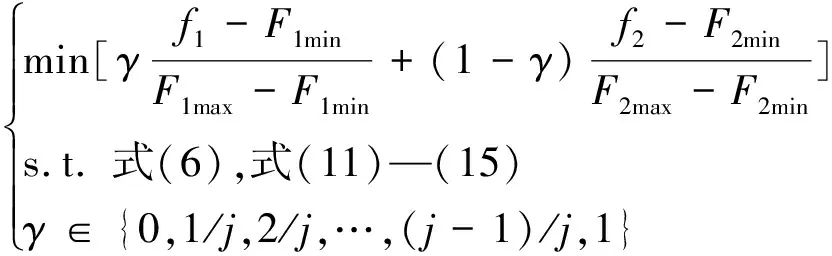
(18)
式中:F1min、F2min分别为目标f1和f2的最小值;F1max、F2max分别为目标f1和f2的最大值;γ和(1-γ)分别为f1和f2的权重;j为权重划分段数。
式(16)所描述的优化模型中,目标函数为线性函数,约束条件包括线性等式和线性不等式,且变量中包含连续变量和整数变量,因此式(16)为混合整数线性规划(mixed-integer linear programming,MILP)模型。式(17)和式(18)所描述的优化模型中,目标函数中包含二次项,约束条件包括线性等式和线性不等式,且变量中包含连续变量和整数变量,因此式(17)和式(18)为混合整数二次规划(mixed-integer quadratic programming,MIQP)模型。
目前混合整数规划求解方法分为精确解法和启发式解法,其中精确解法包括分支定界、割平面法等,启发式算法包括模拟退火、遗传算法和粒子群算法等[22]。随着数学规划理论和计算机技术的发展,凭借优异的求解性能,商业求解器(如CPLEX)广泛应用于MILP和MIQP求解[23-24]。CPLEX求解器中通常采用分支-割平面法求解混合整数模型,并融合了预处理和启发式等多种方法[23]。分支定界法和割平面法属于全局最优算法[25],因此利用CPLEX求解器求解MILP和MIQP可求得模型的最优解,而启发式算法一般无法保证所得解为全局最优解。综上,本文应用CPLEX求解器求解式(16)—(18)所述模型。
步骤3:基于模糊隶属度函数计算各个Pareto最优解的满意度,该指标越小,对应的Pareto最优解的满意度越高。
(19)
式中:δk,e和fk,e分别为第k个Pareto最优解第e个优化目标的模糊隶属度和函数值;Sk为第k个Pareto最优解的满意度指标。
步骤4:选取满意度最大的优化方案,作为最优折中解。
p=argmin{Sk},∀k=1,2,…,j+1
(20)
3 算例分析
3.1 算例介绍
应用本文方法对某区域冬季居民用能进行多目标优化,该耦合DEC的居民用能系统如图2所示,区域能源中心包含光伏发电、蓄电池、电锅炉、微型燃气轮机和燃气锅炉。居民侧能源转换设备包括热水器和空调热泵。参考文献[9]和文献[26],各设备参数见附表A1和A2所示,从上级能源系统购入电能和天然气的价格曲线如附图A1所示。居民热负荷包括采暖负荷和热水负荷,供暖区域面积为3 000 m2,室外温度和冷水温度曲线如附图A2所示,室内舒适度范围取(25±2)℃,热水舒适温度取(53±3)℃。居民除空调热泵和热水器输入功率之外的电负荷和热水需求量预测曲线如附图A3所示,光伏出力曲线如附图A4所示。

图2 某区域耦合DEC的居民用能系统
由第1节所述的耦合DEC的居民用能系统通用化建模方法,推导本算例模型。各能源功率向量具体表达形式、能源转换设备和能源转换电器的输入关系矩阵NC1和NUC1、输出关系矩阵NC2和NUC2、能源转换关系矩阵B1和B2见附录B。
将上述能源功率向量和关系矩阵代入式(6),可得耦合DEC的居民用能系统能源功率平衡方程,即:
(21)
式中:LUR,el和LUR,he分别为居民用户除能源转换电器输入功率的电负荷和热负荷;EACH和EEWH分别为居民空调热泵和热水器输入的电功率;EBUY,el和EBUY,ga分别为居民用户从上级能源系统购入的电能和天然气;EPV为光伏发电供给的电功率;EDIS和ECH分别为电池储能的放电和充电功率;EEB为电锅炉输入的电功率;ECHP和EGB分别为微型燃气轮机和燃气锅炉的输入天然气功率;ηACH和ηEWH分别为居民空调热泵和热水器的产热效率;ηCHP,el和ηCHP,he分别为微型燃气轮机产电和产热效率;ηEB和ηGB分别为电锅炉和燃气锅炉的产热效率;ηACH等能源转换效率前的数值3 600为kW转kJ的单位转换系数。
3.2 多目标优化调度结果
在配置为3.50 GHz,12 GB RAM,工作环境为Windows 7系统的电脑上,基于Matlab2014a平台编码,通过YAlMIP分别调用CPLEX求解器分别求解式(16)和式(17)所示的优化模型,得到目标函数f1和f2的最大值和最小值:F1max=16 795元,F1min=6 037.2元,F2max=0.181 8,F2min=0。进一步设定目标函数权重划分段数j=100,γ{0, 0.01, … ,0.99, 1.00},在各个权重下求解式(18),得到居民用能优化的Pareto前沿,如图3所示。
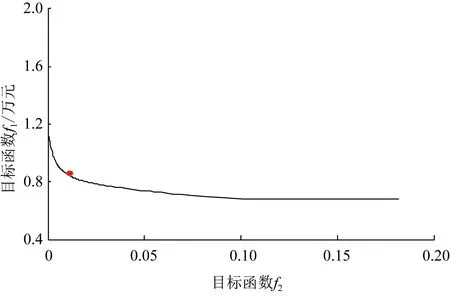
图3 区域居民用能优化的Pareto前沿
由图3可知,居民购能成本与居民不舒适度成反比关系,居民不舒适度越低,需要的购能成本越高。以居民购能成本最低和居民不舒适度最小为目标的单目标优化结果分别位于Pareto前沿的两端。
进一步,根据2.3节步骤3中的式(19)和式(20),计算各个Pareto最优解的满意度,选取满意度最大的优化方案,作为最优折中解,最优折中解已在图3中用红色圆形标识。最优折中解下的居民用户用能来源分布,如图4所示。
由图4可知,居民的电能供应主要来自电网购能和光伏发电,同时,电池储能在电价高峰时段释放小部分电能。用户的热能主要由居民的空调热泵和热水器供应,在热能需求高峰期(06:00—20:00),燃气锅炉提供部分热能,电锅炉功率有限,供给的热能较少。这是因为天然气价格比电价高,为节约用户成本,优先使用电能满足用户需求,当电转热电器和设备(空调热泵、热水器和电锅炉)产生的热能无法满足需求时,燃气锅炉开始工作供给热能。

图4 最优折中解用户用能来源分布
进一步,对比分析单目标优化解和最优折中解的优化目标值、购电量、购气量对比如表1所示。
表1中,折中最优解和f1最优结果的购电量一样多,但折中最优解的购气量高于f1最优结果的购气量,这部分购气成本显著降低了用户的不舒适度;f2最优结果用户的不舒适度为0,但相比折中最优解购能成本多了一倍。最优折中解可在节约用户用能成本的同时,兼顾用户不舒适度影响较小,相对单目标优化而言可综合考虑多方面,可作为微能源网多目标优化调度方案。
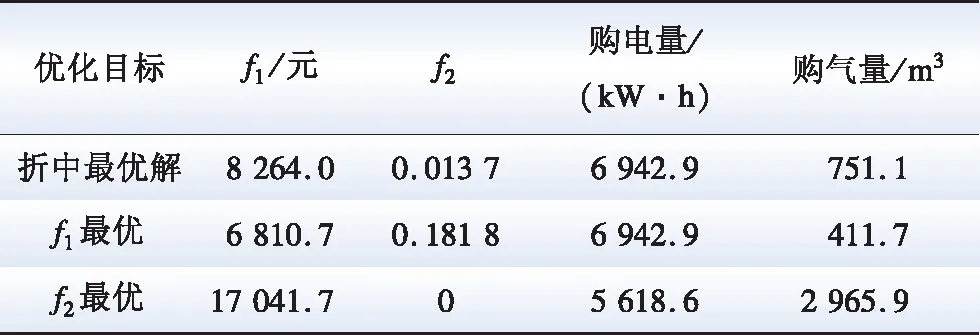
表1 不同优化目标结果对比
3.3 对比分析
为分析居民用户能源转换电器在居民用能优化改善中的作用,本节对比分析了本文所提方法与文献[13]所提方法的应用效果。文献[13]将居民用能设定为固定负荷曲线,通过优化DEC运行实现居民用能优化的目的。在3.1节算例数据的基础上,设定用户使用的热水和室内温度为理想温度,根据式(8)计算得到用户的热负荷曲线,如附图A5所示。文献[13]应用场景下,用户的热负荷完全由DEC中能源转换设备供应,为满足用户需求,此时需要加大能源转换设备的容量,设备容量参数如附表A3所示。本文所提方法和文献[13]在考虑用户舒适性最优下的用能成本情况如表2所示。
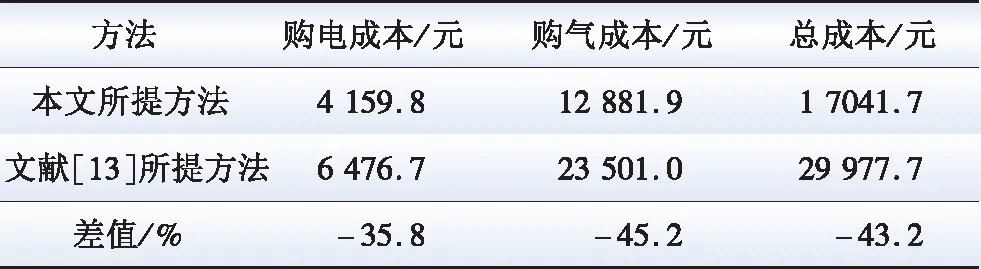
表2 2种方法用户用能成本对比
由表2可知,本文所提方法的各项成本均低于文献[13]中的用能优化方案,其中本文所提方法的总成本相比文献[13]所用方法降低了43.2%,反映了本文所提方法的优越性。同时也表明,居民用户能源转换电器的重要作用,其和DEC优化运行,可有效减少居民用能的成本。
4 结 论
1)所构建耦合DEC的居民用能模型,调整关系矩阵参数即可适应不同场景,适用于复杂系统,具有通用性;
2)所提居民用能多目标优化模型,兼顾用户的经济性和舒适性,能够为用户提供考虑多要素的用能优化方案;
3)空调热泵、热水器等居民能源转换电器与DEC耦合协调运行,可有效改善居民用能效益。
附录A
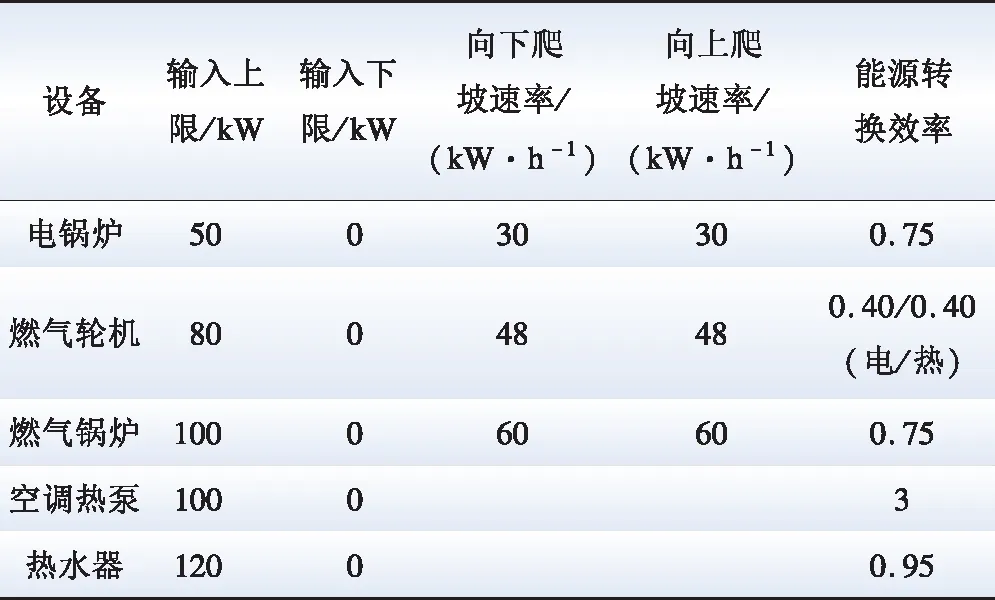
表A1 能源转换设备和电器参数

表A2 能源储存设备参数
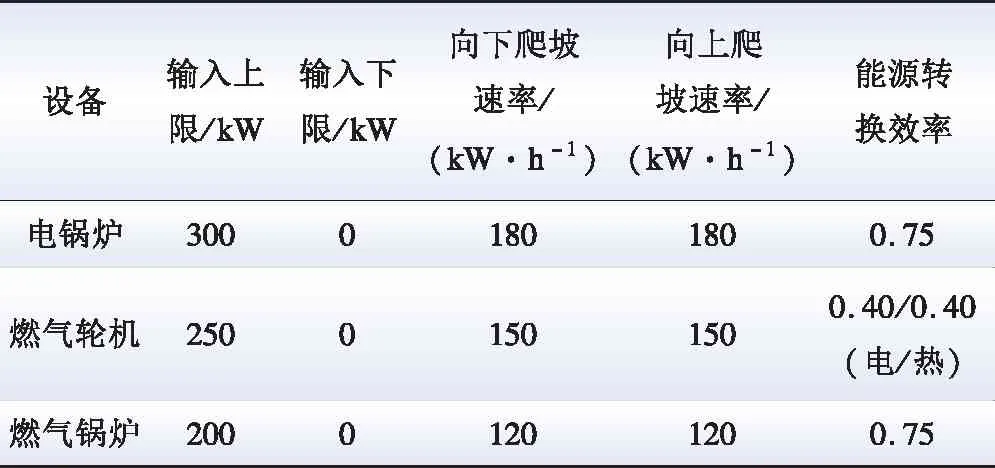
表A3 文献[13]应用场景下能源转换设备和电器参数

图A1 电价和天然气价格时序曲线
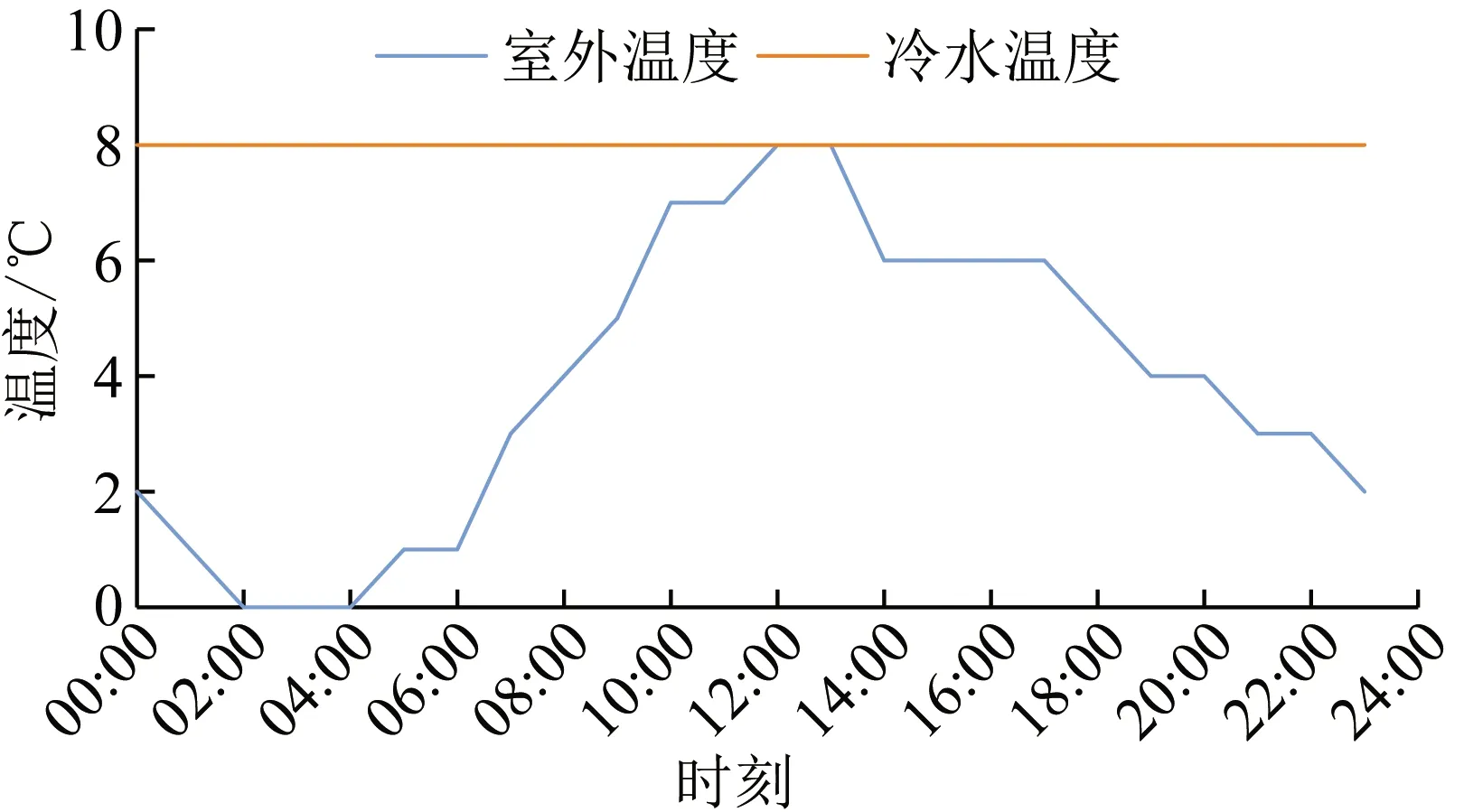
图A2 室外温度和冷水温度曲线
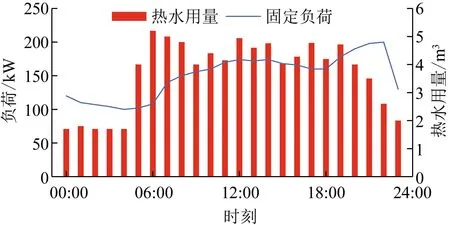
图A3 居民电负荷和热水需求量预测曲线
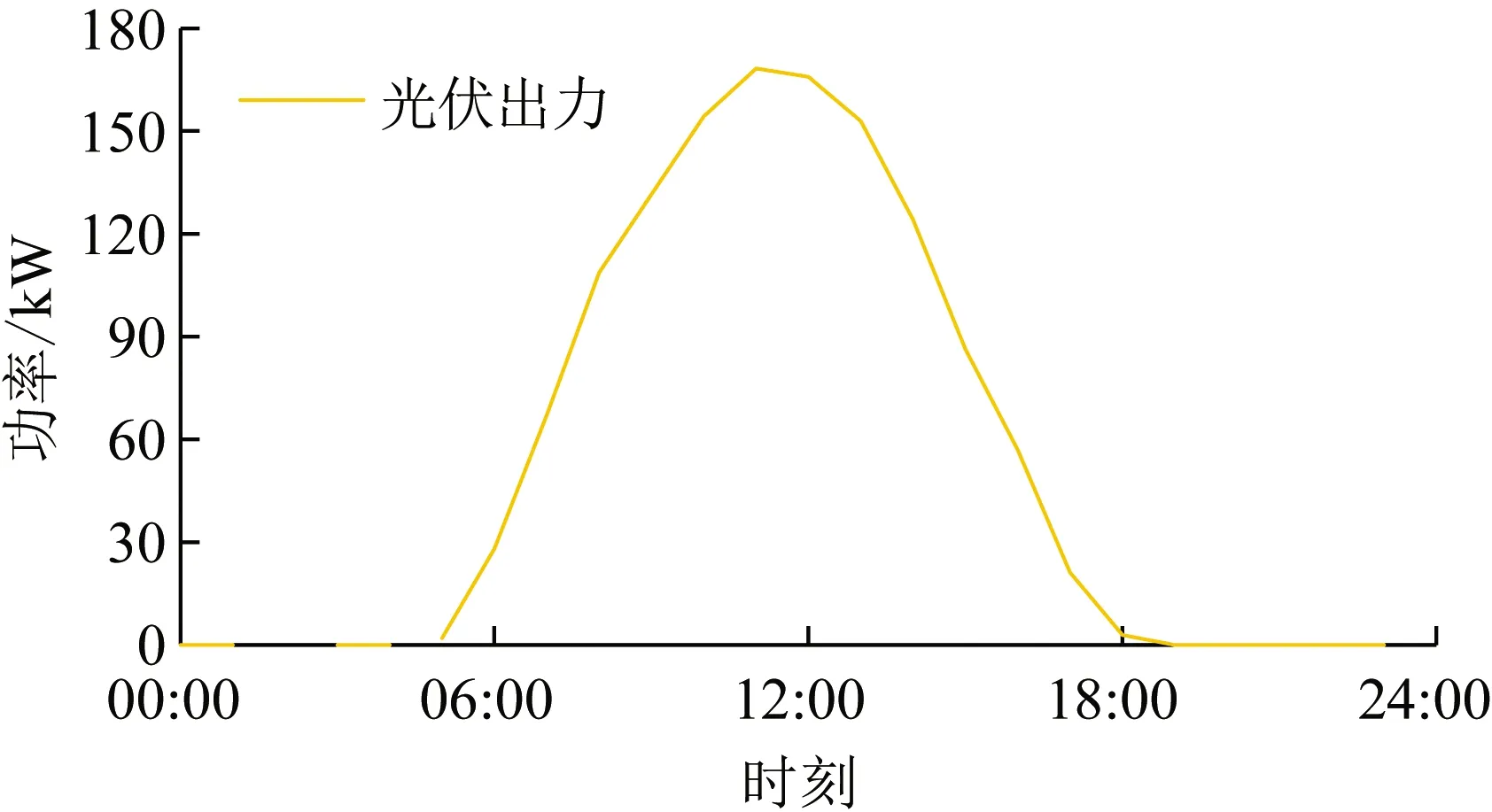
图A4 光伏出力曲线
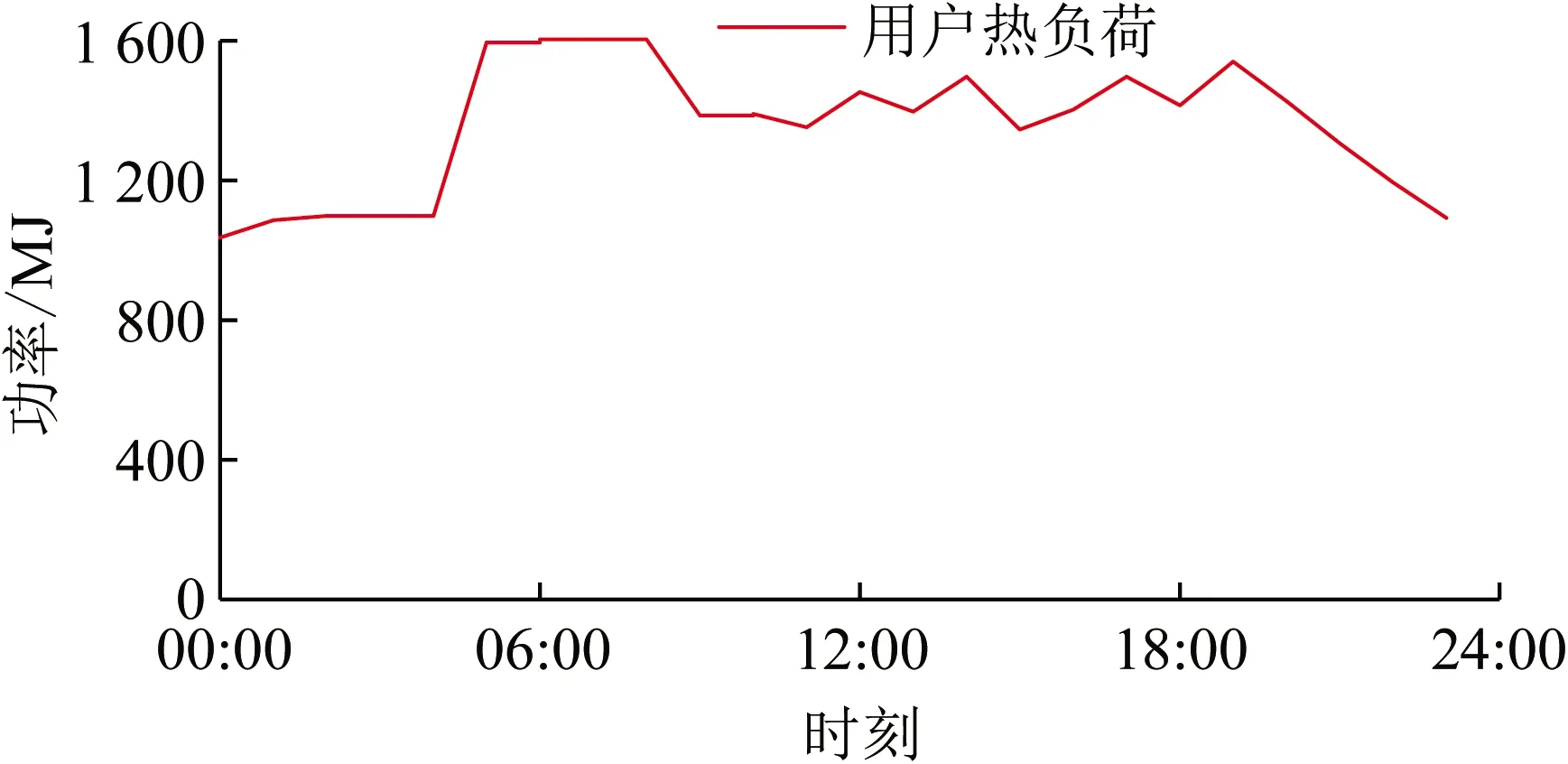
图A5 用户的热负荷曲线
附录B
定义能源功率向量如下:
(B1)
式中:HACH和HEWH分别为居民空调热泵和热水器的输入功率;EEB,he、ECHP,he和EGB,he分别为电锅炉、微型燃气轮机和燃气锅炉的输出的热功率;ECHP,el为微型燃气轮机输出的电功率。
(B2)
(B3)
(B4)
(B5)
(B6)
(B7)

