大型输水管桥动力特性及水锤效应作用下动力响应研究

张 博，张嘉瑞，曹双利，连阳阳，宋志强

(1.中国电建集团西北勘测设计研究院有限公司，西安 710065;2.西安理工大学，西安 710048;3.陕西省引汉济渭工程建设有限公司，西安 710024)

0 前 言

输水管桥在正常使用情况下管道荷载约为同宽度车道荷载的7倍，其受力不同于普通公路斜拉桥和铁路斜拉桥，在非恒定流水作用下，流速变化会在管道中产生一系列压力交替变化的水力冲击，水锤效应明显。在水-管-桥三者的耦合作用下，结构受力十分复杂。

国内外已建的输水管道铺设在桥梁上的工程案例有上海东海大桥在箱梁内敷设2根直径为0.5 m的供水管[1]，浙江温州在大门大桥主梁上敷设2根直径为1 m的供水管道[2]，美国的San Joaquin桥梁共敷设了6根直径为1.8 m的管道[3]。在理论研究方面，庄小将采用管道-桥梁耦合体系，将水锤以机械波的形式施加，研究了管道周期性振动对大门大桥的威胁[2]。孙建渊等建立输水管道水锤计算模型和斜拉桥结构动力模型得到了水锤冲击作用下斜拉桥结构动力响应[4-5]。伍平、戴安达等通过双向流固耦合数值模拟与实验相结合，评价了输水管道与桥梁结构发生共振的可能性，研究了水-管-桥耦合系统的振动特性[6-7]。但针对大流量、大跨度的斜拉压力输水管桥的动力特性及水锤效应相关研究较少。

引汉济渭工程是陕西省境内一项跨流域调水工程，也是关系陕西未来经济社会发展的战略性工程，是国务院确定的172项重大水利工程之一。工程对实现陕西水资源优化配置、统筹关中陕北用水，促进陕南循环经济，提升治理渭河水生态环境，推动全省实现区域协调可持续发展具有重要意义。随着一期调水工程建设接近尾声，2021年6月，输配水干线工程(引汉济渭二期工程)也已开工建设。引汉济渭二期工程主要由黄池沟配水枢纽和南北两条干线组成，其中北干线大流量压力管道跨越渭河采用大跨度、多塔斜拉管桥结构，管桥总长1.346 km，标准断面宽16.5 m，桥上敷设2×DN3400 mm输水压力管道，其规模在国内同类输水管桥中居前列。斜拉管桥作为过渭干线工程的关键建筑物，若在运行期间遭受水锤效应等作用发生破坏，将严重影响过渭干线的高效输配水，将使得引汉济渭工程效益无法充分发挥。

本文以渭河斜拉输水管桥为工程背景，建立管桥有限元分析数值模型，分析输水管道和斜拉桥的动力特性，研究水锤效应对桥梁主要构件的动力响应，分析不同水锤冲击荷载施加方式对管桥动力响应的影响，以期对管桥结构设计提供技术参考。

1 工程概况

渭河斜拉管桥主桥长490 m，为4塔5跨斜拉桥，跨径布置为(65 m+3×120 m+65 m)，标准断面宽16.5 m；主塔采用水滴形混凝土结构，桥塔总高73.5 m，上塔柱44.5 m，下塔柱高29.0 m，横向宽约28 m，截面为3.5 m×4.5 m；主梁采用钢桁梁结构(包括下弦杆、上弦杆、腹杆等)，桁内净宽16.5 m，桁架高约9.3 m；双索面布置，斜拉索间距8.0 m，单塔布置12对，全桥共布置48对。桥面敷设2根Q345D压力输水钢管，管道内径为3.4 m，管壁厚22 mm，斜拉管桥总体布置如图1所示。

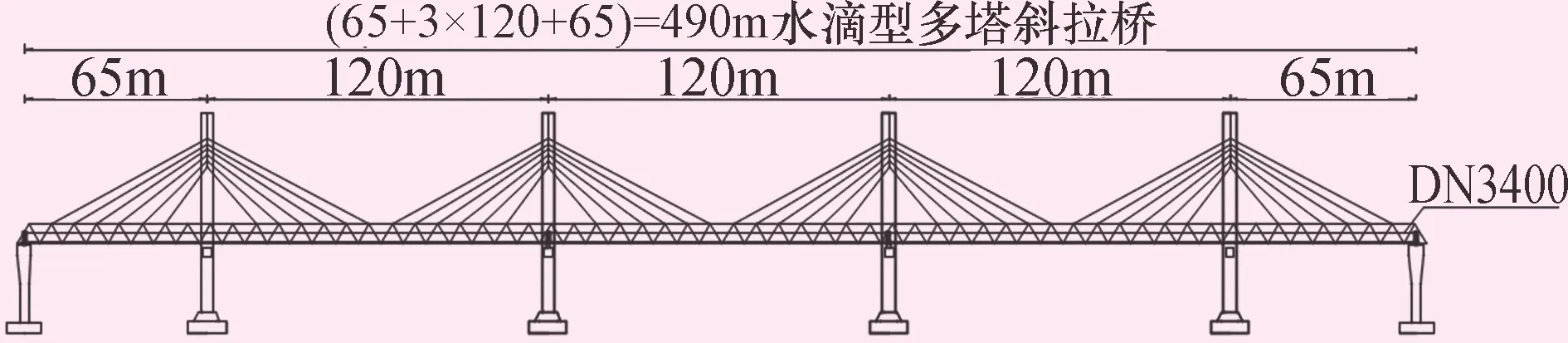
图1 斜拉管桥布置示意

2 有限元模型建立

采用有限元软件ANSYS进行管桥系统的有限元模型建立及分析。模型为三维空间结构，水滴型桥塔、主桥横梁承台、桥墩采用实体单元SOLID45单元模拟。钢筋混凝土纤维桥面及压力输水管道、钢镇墩采用板壳单元SHELL63单元模拟，钢桁梁上、下弦杆及腹杆、横梁、K型支撑杆采用梁单元BEAM188单元来模拟[8]。管道按照间隔设置边界条件，模拟管道支墩的影响。每个支墩约束管道的横向、竖向自由度，管道在顺桥向可以自由运动。镇墩与管道按固定连接模拟，约束管道各向平移和转动自由度。斜拉管桥单跨有限元模型如图2所示。

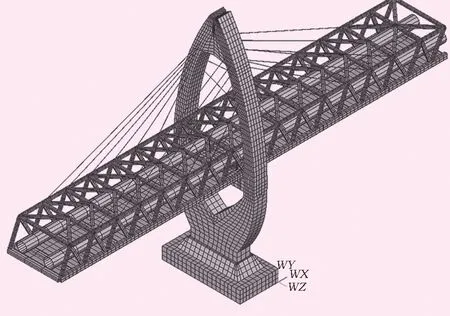
图2 斜拉管桥单跨有限元模型

3 输水管道与斜拉桥振动特性分析

考虑管道施工完建(无水)和正常运行(有水)两种工况进行输水管道与斜拉桥固有频率对比分析，管道内水体采用附加质量模拟。斜拉桥与输水管道的动力特性计算结果如表1所示。

由表1可见，斜拉桥的自振频率呈现频率低且振型密集的特点，符合长周期结构的固有动力特性特征。斜拉管桥前十阶自振频率与输水管道有水、无水情况下的前十阶自振频率错开度均较大，低阶频率无交叉部分，即输水管道供水工况变化导致水力激励引起的管道振动对桥梁结构影响不大，二者不具备发生共振的可能性。

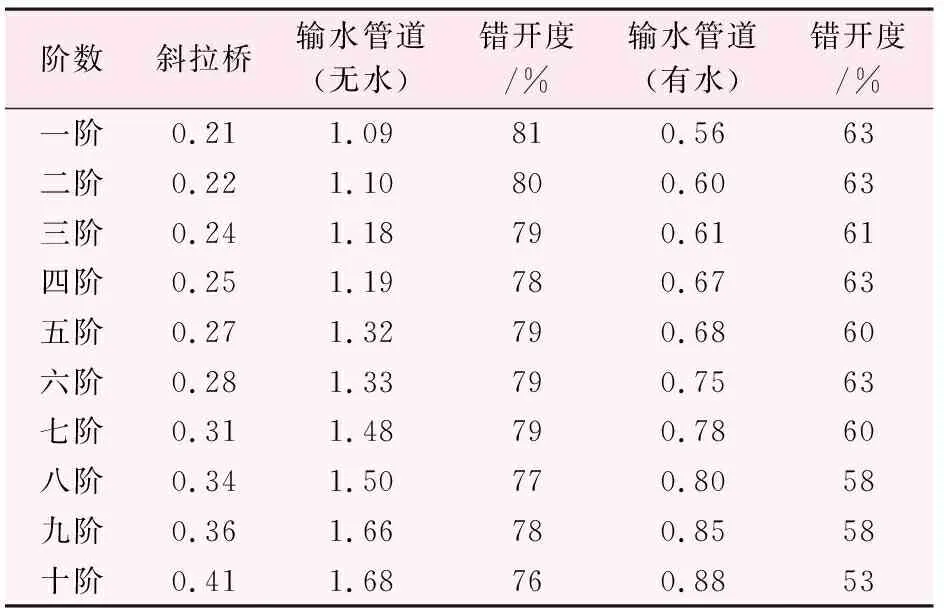
表1 斜拉桥与输水管道前10阶固有频率计算结果 /Hz

考虑管道按间隔设置约束的长度及斜拉桥桥面厚度变化，对管道和斜拉桥自振频率的影响,计算结果如图3、4所示。

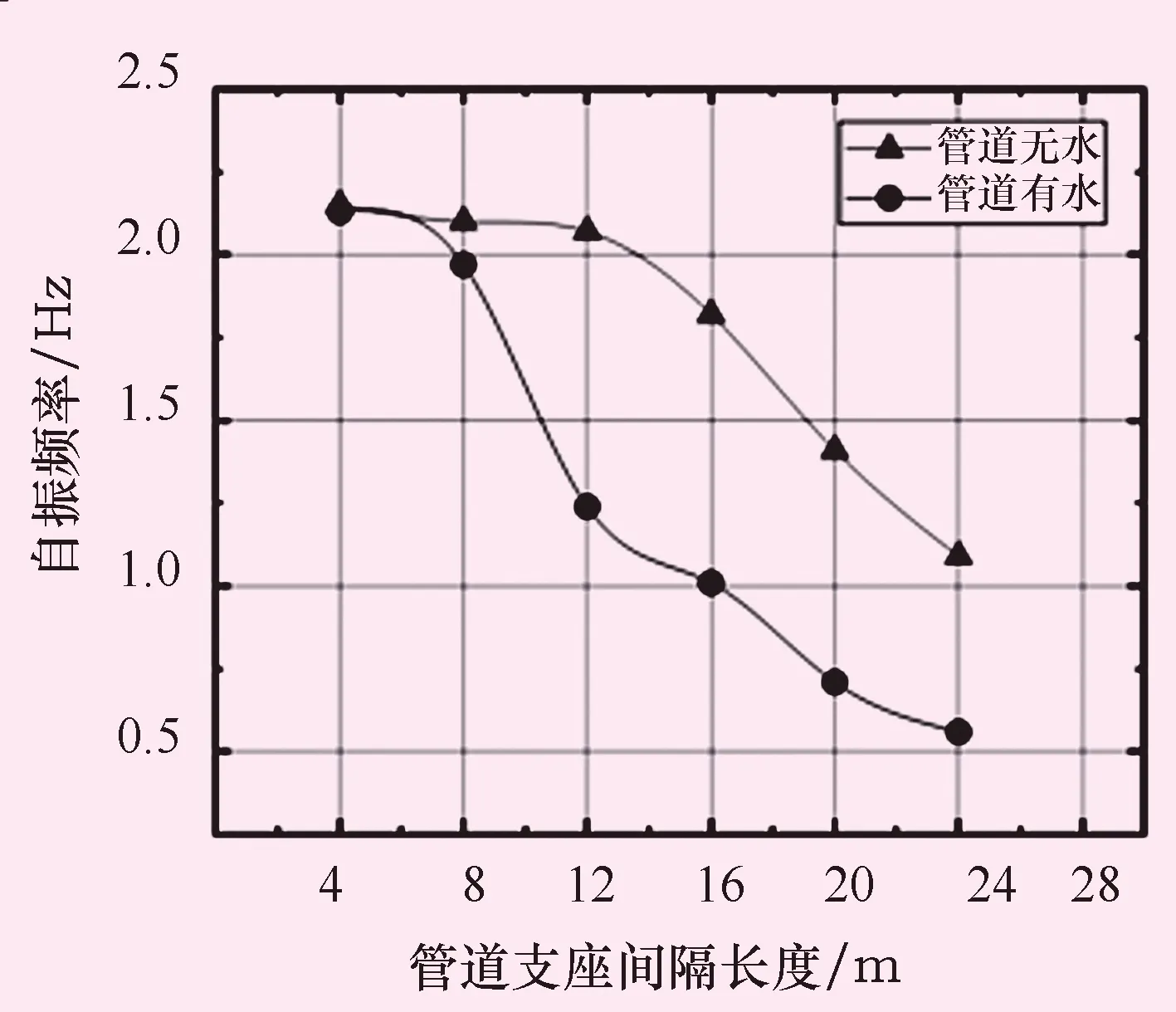
图3 管道自振频率随支座约束变化规律

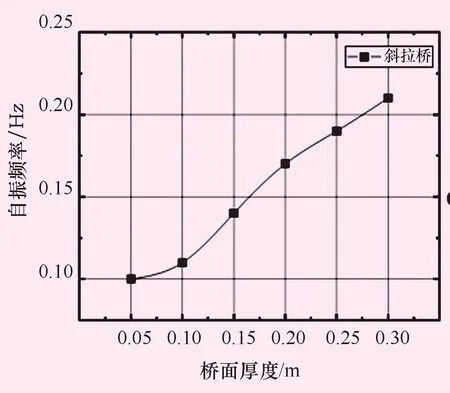
图4 斜拉桥自振频率随桥面厚度变化规律

从图3可以看出，无论在无水或有水工况，随着支座约束的间隔长度增加，管道基本自振频率呈非线性递减趋势。而从图4中可知随着桥面厚度增加，斜拉桥基本自振频率大致呈线性递增趋势；支座约束间隔长度为24 m时管道(有水)自振频率为0.56 Hz、桥面厚度为0.3 m时斜拉桥固有频率为0.21 Hz，二者仍然不具备发生共振的可能性。适当增加管道支座的数量，减少支座间隔及控制桥面的厚度，更加有利于控制输水管道和桥梁发生共振。

4 水锤冲击下管桥系统动力分析

4.1 水锤冲击作用

在压力管道正常输水过程中当阀门突然关闭，管道内流量的急剧变化将在管道内引起压强的显著变化，这种水力现象称为水锤效应。当管道内发生水锤现象时，能量以机械波的方式传递，由于流速和流量的突变而产生的沿管道纵向冲击力，对结构的动力响应有较大影响。本文根据大型输水管道供水工况转换时的水力过渡过程计算结果，选取设计流量下300 s关阀时间产生的水锤压力时间历程作为管桥动力响应分析的冲击荷载进行计算。其中水锤动水压强如图5所示，从图中可以看出，水锤冲击力的变化基本呈周期性正弦形式，并迅速衰减，水锤冲击力最大值为1 804.43 kN。将水锤冲击荷载均匀施加在斜拉管桥桥塔12个固定钢镇墩上(每组2个钢镇墩顺桥向对称分布)，如图6所示。同时为了研究水锤冲击荷载不同施加方式对动力响应的影响，按距离阀门位置距离的由近到远，考虑了不同镇墩承担比例的不同，按6∶5∶4∶3∶2∶1施加在桥塔12个钢镇墩上，与均匀输入相比，研究斜拉桥构件在非均匀输入情况引起的管桥构件的附加内力情况。

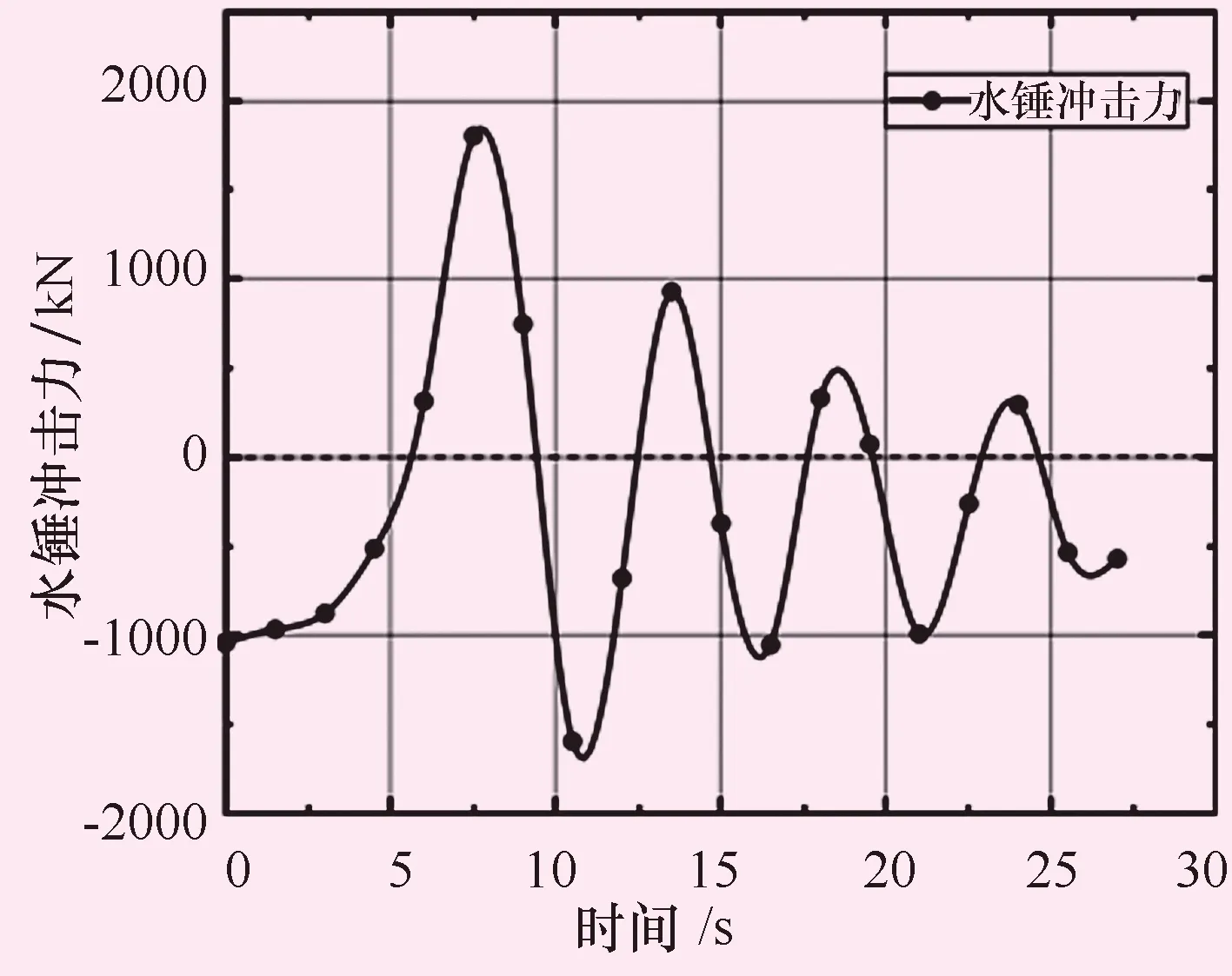
图5 300 s关阀水锤冲击力变化曲线

4.2 管桥系统结构动力响应分析

表2给出了钢桁架梁下弦杆、上弦杆和腹杆、横梁、斜拉索以及桥塔在不同水锤冲击作用加载方式下得到的动力响应最大值。由表2中可见，在水锤冲击作用下，管桥各构件动力响应均以顺桥向为主，其中钢架梁的位移及应力响应幅值不大，顺桥向位移仅为1 mm量级，横向弯曲应力仅为1 MPa量级，竖向弯曲应力相对较小；塔顶顺桥向位移与拉索应力响应值相对较大。下弦杆顺桥向位移1.07 mm，塔顶顺桥向位移2.56 mm，斜拉索应力变幅为12.67 MPa，大部分拉索应力值为增幅。

图6 水锤冲击力计算模型

与均匀施加相比，将水锤冲击荷载不均匀按比例施加在主桥镇墩上所得各构件结构动力响应值更大，各构件之间不均匀的相互作用给管桥构件带来更强的附加内力效应。如下弦杆顺桥向位移增大55%，达到1.66 mm，塔顶顺桥向位移增大39%，达到3.56 mm，钢桁梁下弦杆、上弦杆和腹杆及桥面主梁的横向弯曲应力均有大幅提升，最大增加1倍左右，如下弦杆横向弯曲应力由0.58 MPa增加至1.07 MPa，腹杆由0.4 MPa增加至0.75 MPa等。斜拉索应力变幅和塔底应力相对受不均匀水锤荷载引起的附加内力效应影响较小。可以看出，尽管各构件位移和应力相对均匀施加有较大增加，但仍然处于正常使用极限和安全承载能力极限范围内，不会影响构件的正常使用，更不会对构件的安全产生较大的危险。

图7、8给出了均匀施加情况下弦杆顺桥向位移和横向弯曲应力在不同节点位置的分布情况。从图8中可以看出，下弦杆顺桥向位移最大值位于最左端节点处，即最靠近水锤冲击荷载位置处，节点顺桥向位移随着节点编号的增大而逐渐降低到0.4 mm左右。下弦杆的竖向位移相对较小，在5号节点处最大，达到0.4 mm,横桥向位移更小。顺桥向的水锤冲击力主要使得下弦杆产生横向的弯曲作用，最大弯曲应力达到0.58 MPa，主要发生在靠近水锤冲击作用位置的跨中截面，在顺桥向其他位置截面，横向弯曲应力迅速降低。下弦杆截面应力变化幅度不超过1 MPa量级，水锤冲击作用对下弦杆的影响不大。水锤荷载不均匀施加下弦杆等构件的空间位移和截面弯曲应力分布情况类似。

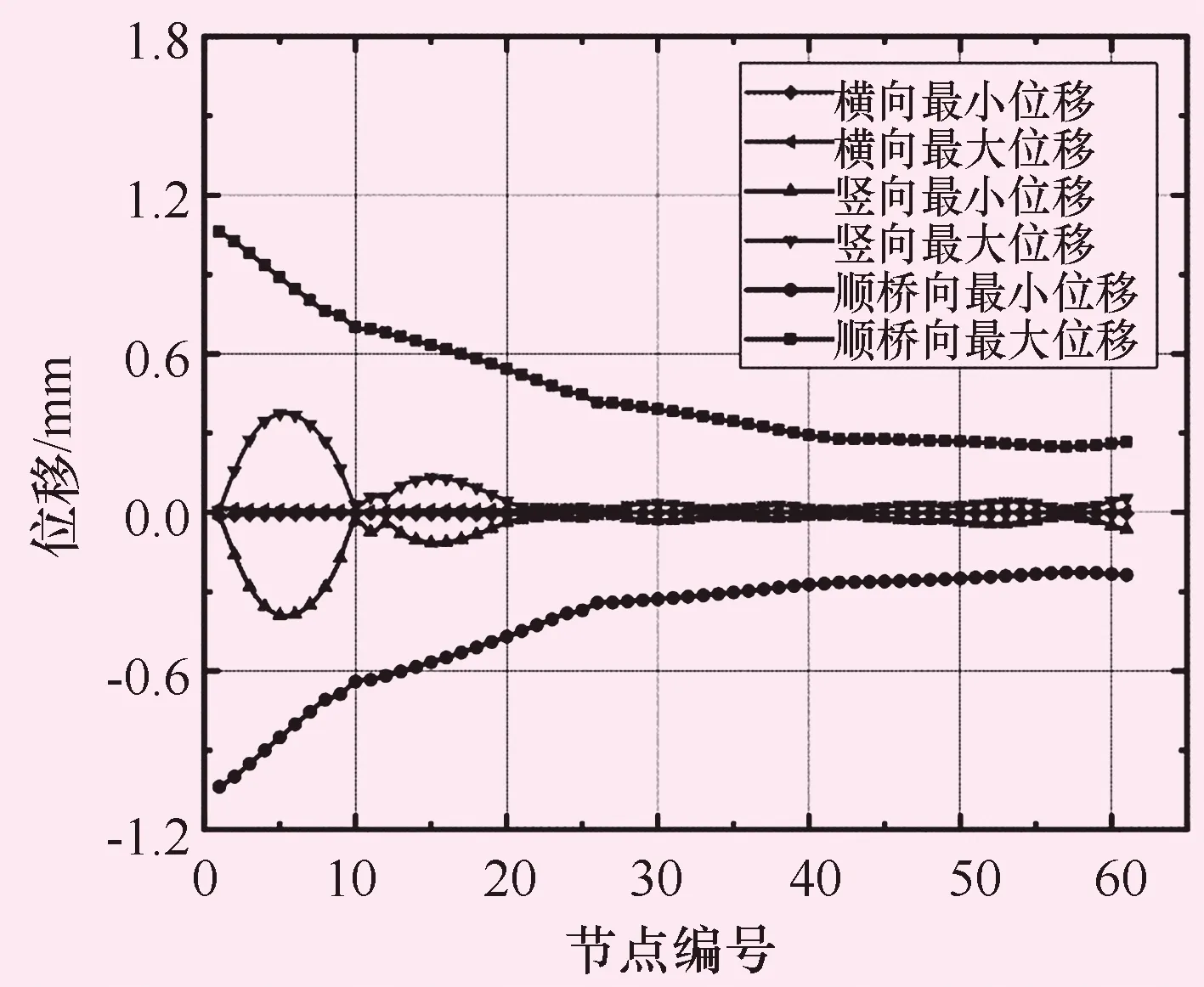
图7下旋杆不同位置位移幅值

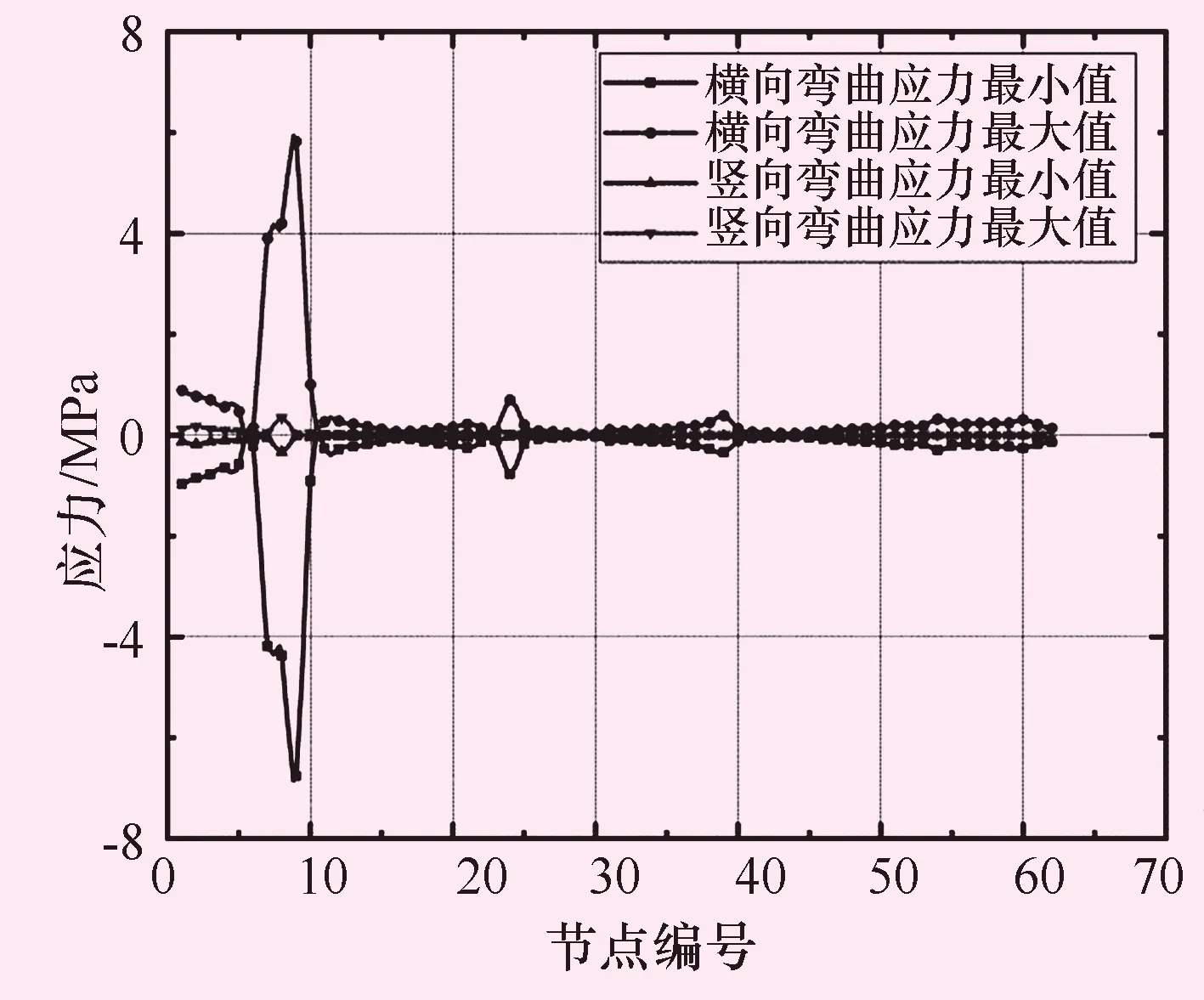
图8下弦杆不同位置截面弯曲应力幅值

表2 水锤冲击作用下斜拉管桥主要构件结构动力响应

图9给出了桥梁一侧拉索(由于应力对称分布，仅取桥体一侧方向的拉索)在水锤冲击过程中的应力极值及应力变幅值。拉索编号如下：由上游至下游主塔A、B、C、D上斜拉索编号分别为A组、B组、C组、D组，每组索按顺桥向从靠近上游阀门位置开始依次编号为1-12。斜拉索应力幅值变化过程曲线见图10。由图10可见，应力变化幅度最大的拉索位于A塔的第7根拉索位置，最大值达6 MPa，同样位置附近出现较大的应力变幅，最大应力变幅在12 MPa左右。主要是由于塔体和主梁的不协调变形所致，其他各塔在塔体附近的拉索也有类似情况，只是在幅值上略低。在验算水锤作用下斜拉索动应力时，应对各塔附近位置处的拉索需要予以关注。图10给出了A组应力较大的1号、7号和12号拉索在计算时间内的应力变化曲线，可以看出各索应力变化规律基本一致，应力变化频率较快，当拉索应力出现负值时，并不代表拉索受压，而是拉索相对于水锤冲击力作用前的拉力降低。

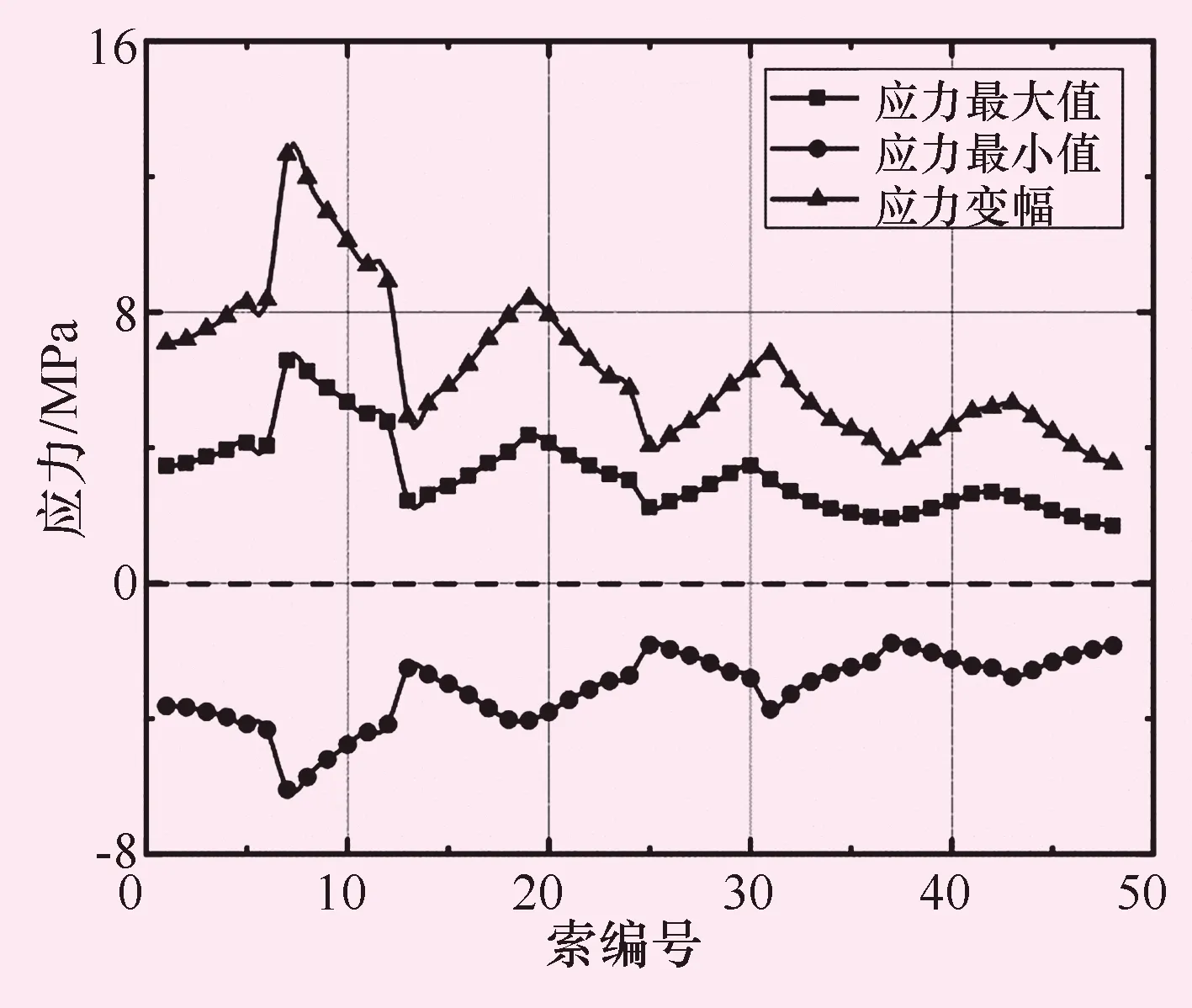
图9 斜拉索应力幅值及变幅

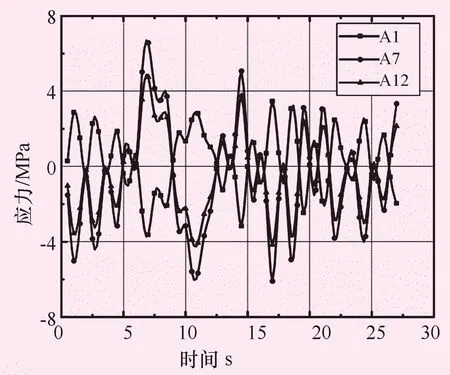
图10 斜拉索应力幅值变化过程曲线

5 结 论

以跨渭大型输水管桥为工程背景，建立了管桥有限元分析模型，在分析了输水管道、斜拉桥的固有动力特性的基础上，进行了管、桥共振复核，分析了水锤冲击荷载作用下桥体主要构件的动力响应，具体结论如下：

(1) 综合分析了管道有水、无水情况下，输水管道前十阶自振频率与斜拉桥前十阶自振频率无交叉，错开度较大；当输水管道因水力激励而发生振动时，桥梁结构不会与之发生共振；通过管道支墩约束间隔以及斜拉桥桥面厚度对管桥系统固有频率的敏感性分析可知，适当增加管道支墩的数量，减少支墩间隔，控制桥面主梁的厚度，能进一步增大管、桥的固有频率错开度。

(2) 在顺桥向水锤冲击荷载作用下，桥梁主要构件的动力响应以顺桥向为主，其中钢架梁的位移变化不大，顺桥向位移仅为1 mm量级，横向弯曲应力仅为1 MPa量级，塔顶顺桥向位移2.56 mm，斜拉索应力变幅为12.67 MPa，大部分拉索应力值为增幅。

(3) 与均匀施加相比，将水锤冲击荷载不均匀施加在主桥镇墩上所得各构件动力响应值更大，不均匀荷载激励作用给管桥构件带来更强的附加内力效应，如下弦杆顺桥向位移增大55%，塔顶顺桥向位移增大39%。斜拉索应力变幅和塔底应力受不均匀水锤荷载引起的附加内力效应影响较小。尽管各构件位移和应力相对均匀施加有较大增加，但仍然处于正常使用极限和安全承载能力极限范围内。

(4) 下弦杆顺桥向位移最大值位于最靠近水锤冲击荷载位置的最左端节点处，横向的最弯曲应力主要发生在靠近水锤冲击作用位置的跨中截面。斜拉索应力化幅最大发生在位于A塔的第7根拉索，主要是由于塔体和主梁的不协调变形所致，在验算水锤作用下斜拉索动应力时，应对各塔附近位置处的拉索予以关注。