多监测项目联合的大坝安全监控模型

王丽蓉，郑东健

(1.中国电建集团西北勘测设计研究院有限公司，西安 710065；2.河海大学水利水电学院，南京 210098)

0 前 言

建立大坝安全监控模型，可以预测监测值变化趋势，解释主要荷载对监测效应量变化的影响，拟定监控指标。统计模型是应用最广的大坝安全监控模型，以水压、温度、降雨和时效为主要影响因素，建立回归模型[1-2]。若统计模型的各分量部分或全部采用有限元分析拟合的表达式，则为混合模型或确定性模型[3-4]。近年来，支持向量机模型M[5-6]、神经网络模型[7-8]、灰色预测模型[9]等采用新兴算法的大坝安全监控模型也被广泛研究。上述大坝安全监控模型一般是针对同一监测项目单测点或多测点进行建模。实际上，大坝各监测项目的测点监测资料是大坝安全工作状态的不同层次、不同角度的反映，是大坝安全状态监测信息整体的不同部分。大坝各监测项目如变形、渗流、应力应变均同时受到上下游水位、气温、降雨等环境量的影响，在工作性态相似的大坝区域，各监测项目的变化存在同步性和相似性。基于监测的整体信息建立安全监控模型，有助于挖掘信息的内在联系，从监测信息整体角度监控大坝安全状态。如何从时间和空间上，反映各监测项目各测点的内在逻辑关系，是建立整体信息联合安全监控模型的关键。

卷积神经网络(Convolutional Neural Network，CNN)具有学习数据内在空间相关规律的能力，长短时记忆网络期记忆神经网路(Long Short-Term Memory，LSTM)是一种专门处理时序数据的神经网络。ConvLSTM(卷积长短时记忆网络)集成了LSTM处理时间维信息的能力和卷积层处理局部强相关数据的优势，允许多组测值形成一个矩阵进入网络，并且具有获取测点相关性信息的能力。但卷积层提取关联信息的位置有限，一旦网络搭建完毕，ConvLSTM只能注意到固定几组测点的相关性。同时，监测值总是随时间动态变化，测点相关度也同步变化，若卷积层跨度不足，那么ConvLSTM会忽略部分测点相关性，模型的精度会受到影响。动态时间规整算法(Dynamic Time Warping，DTW)可以规整由于测点位置和监测项目不同，各个监测序列变化的不同步，从而增强模型提取测点相关性的能力。为此，本文在分析卷积长短时记忆网络和动态时间规整算法基本原理的基础上，融合ConvLSTM模型和DTW算法的优势，构建大坝安全监测整体信息联合监控模型，以提高模型监控大坝整体安全状态的能力。

1 卷积长短时记忆网络的建模原理

长短时记忆网络是一种专门处理序列数据的深度神经网络，由循环神经网络(Recurrent Neural Network ,RNN)引入门控系统而来[10]。LSTM难以处理带有很强局部相关性的空间数据，卷积层(Conv)与LSTM结合的卷积长短时记忆网络(ConvLSTM)能够更好地捕捉时空相关性[11]。网络中卷积层提取每时刻输入数据的局部关联信息；LSTM提取时间维特征。ConvLSTM扩展了LSTM，使其在输入-状态转换和状态-状态转换中都具有卷积结构[11]，如图1，ConvLSTM不仅有外循环，还有ConvLSTM“细胞”内循环。

图1 ConvLSTM的外循环

时序数据依时步流入相同的ConvLSTM“细胞”。“细胞”前向计算流程如图2所示。

图2 ConvLSTM“细胞”结构

(1) 上一时步的输出信息h(t-1)和当前时步的X(t)作为输入数据进入细胞。

(2) 输入数据分别与4组不同的权值W(i)、U(i)、b(i)；W(f)、U(f)、b(f)；W(o)、U(o)、b(o)；W(C)、U(C)、b(C)进行卷积运算，再通过激活函数，得到输入门i(t)、遗忘门f(t)、输出门o(t)以及C′(t)，见公式(1)。sigmoid激活函数表达式见公式(2)，tanh激活函数表达式见公式(3)。

(3) 当前时步的细胞状态cell(t)是输入门与C′(t)的Hadamard积、遗忘门与上一时步细胞状态cell(t-1)的Hadamard积之和，见公式(4)。

(4) 输出门与经过tanh激活函数的cell(t)求Hadamard积，得到当前时步的输出信息h(t)，见公式(5)。

i(t)=σ[W(i)*h(t-1)+U(i)*X(t)+b(i)]

f(t)=σ[W(f)*h(t-1)+U(f)*X(t)+b(f)]

o(t)=σ[W(o)*h(t-1)+U(o)*X(t)+b(o)]

C′(t)=tanh[W(C)*h(t-1)+U(C)*X(t)+b(C)]

(1)

cell(t)=i(t)oC′(t)+f(t) ocell(t-1)

(4)

h(t)=o(t)o tanh[cell(t)]

(5)

公式(1)～(5)中：i(t)为t时刻的输入门；f(t)为t时刻的遗忘门；o(t)为t时刻的输出门；σ为sigmoid激活函数；tanh为双曲正切激活函数；e为自然数；W(·)、U(·)为网络连接权值；b(·)为偏置；*代表卷积操作；o代表求Hadamard积。图2中σ表示sigmoid激活函数，值在(0，1)之间；tanh表示双曲正切激活函数，值在(-1，1)之间。

2 结合DTW的卷积长短时记忆网络改进方法

卷积层只能提取模型输入数据的局部相关性信息，导致ConvLSTM只能提取输入模型测点中部分测点的相关性。为此，结合动态时间规整算法(DTW)对ConvLSTM进行改进，建立结合动态时间规整算法的卷积长短时记忆网络(DTW-ConvLSTM)，使其获取更为全面的测点相关性信息，用以提高模型的预测精度。

2.1 动态时间规整算法

由于测点位置和监测项目不同，各个监测序列的变化并不同步。因此采用动态时间规整算法(DynamicTimeWarping，DTW)度量监测序列的相关程度更为可靠。

DTW是一种计算2条扭曲轨迹相似度的算法[12]。当两段时间序列具有相似的形状而形状变化在时间轴上不对齐时，DTW对序列在时间轴上进行局部缩放，使得二者形态尽可能一致，从而得到最大相似度。

设两段序列Q={q1，q2，…，qi,…，qu}、C={c1，c2，…，cj,…，cv}，Q的时间长度为u，C的时间长度为v，DTW计算二者相似度的过程为：

(1) 构建u×v大小的矩阵P，P(i，j)=di,j是qi与cj的欧几里得距离，见公式(6)；

(2) 搜寻P从起点P(1，1)到终点P(u，v)的所有路径里距离最短的路径W，最短距离即为Q、C的距离，值越小，Q、C相似度越高。

搜寻最短路径时，至P(i，j)元素的路径累积距离Di,j为di,j与前面元素累积距离的最小值之和，表示为：

Di,j=di,j+min[Di-1,j,Di,j-1,Di-1,j-1]

i=2,…,u;j=2,…,v

(7)

Di,j的初始条件为：

设W={w1，w2，…，wk,…，wK}，wk为P中元素的坐标。W必须满足以下条件：

(1) 边界条件：w1=(1，1)，wK=(u，v)。

(2) 连续性：若wk-1=(a′，b′)，wk=(a，b)，则a-a′≤1，b-b′≤1。

(3) 单调性：若wk-1=(a′，b′)，wk=(a，b)，则a-a′≥0，b-b′≥0。

2.2 DTW融入ConvLSTM

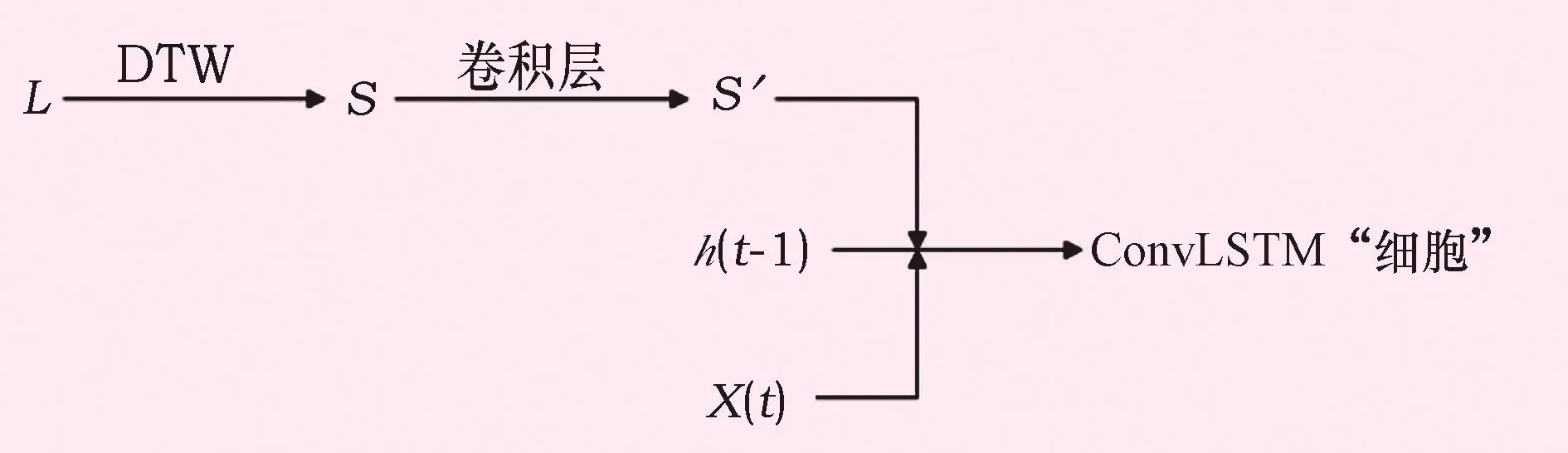
图3 DTW-ConvLSTM结构

将m行n列的矩阵L输入模型，则输入网络的维度转换成[m，1，1，n]，该张量元素从左至右分别是时间维、通道维、高、宽；h(t-1)、X(t)分别是上一时步ConvLSTM“细胞”输出和当前时步输入，维度不包含时间维，分别为[b，1，n]和[1，1，n]，b为隐藏层维数，数值取决于网络设置。用DTW计算L中所有测点相关度，可得到n×n大小的相关度矩阵S。为使S参与网络运算，需将S、h(t-1)、X(t)在通道维拼接，这要求三者高、宽相同。如图3，在拼接前添加两层卷积层，输入维度为[1，n，n]的S(没有时间维)，输出维度为[2，1，n]的S′。S′、h(t-1)、X(t)拼接得到维度为[b+3，1，n]的ConvLSTM“细胞”输入数据。DTW融入ConvLSTM后，网络后续运算与ConvLSTM相同。

3 DTW-ConvLSTM联合监控模型

在置信区间法[13]的基础上，采用DTW-ConvLSTM(结合动态时间规整算法的卷积长短时记忆网络)预测值拟定监控指标，构建DTW-ConvLSTM联合监控模型。由于DTW-ConvLSTM的预测功能，该模型可实现监控指标的预先拟定，并随时间不断更新，帮助及时预警。

DTW-ConvLSTM模型用多个监测项目测点的前m天测值结合水位、气温、降雨量等环境量预测后续m天测值，可预先拟定后续m天的监控指标。多组测值构成的矩阵L输入模型，L包括m个时步n组测值，L为m行n列。模型输出的数据结构与L相同，为m行n列。

DTW-ConvLSTM模型搭建采用编码-解码的结构形式，如图4，编码器将输入数据编码成状态量，解码器将状态量翻译成输出量即预测值，二者分别完成信息提取和预测工作；ConvLSTM“细胞”是模型的核心，与编码、解码器分别形成回路。

图4 编码-解码的网络结构

在历史监测资料中，当DTW-ConvLSTM预测值与实测值的复相关系数R高于0.8时，可用该模型预先拟定监测量的监控指标：

如果实测值落在监控指标内，则认为大坝运行正常；如果实测值超出监控指标之外，并且有趋势性变化，则认为测值异常，应加强监测并分析成因。

4 实例分析

某坝为宽缝式混凝土重力坝，二级建筑物，坝长1 354m，坝顶高程138.80m(黄海高程)，最低基岩高程86.00m，最大坝高52.80m，保坝洪水位138.50m，正常蓄水位133.00m(与设计洪水位相同)，死水位121.50m。库容为3.37亿m3。目前在测观测项目有：大坝变形、渗流、环境量、内部监测4个监测项目。

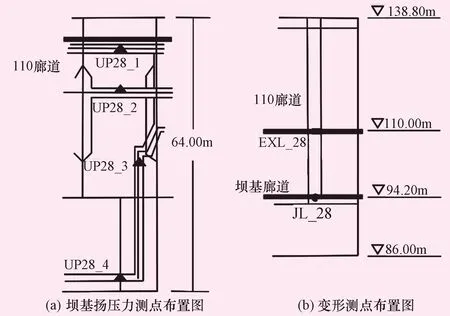
图5 28号坝段测点布置

考虑重力坝的工作特点，针对每个坝段建立多种监测项目测点的联合监控模型。以28号坝段为例，图5为测点布置图，28号坝段共布置有6个监测点，分别为坝基扬压力测点UP28_1、UP28_2、UP28_3、UP28_4，110.00m高程廊道水平位移测点EXL_28，和坝基廊道垂直位移测点JL_28；环境量考虑上游水位、气温和降雨量的影响。用上述包含变形和扬压力的6个测点和3个环境量测点的前6d测值建立DTW-ConvLSTM模型，并预测后续6d测值，将9组测值构成的矩阵L输入监控模型进行训练。L包括6个时步和9个测点的测值，则L为6行9列。针对大小为6×9的输入、输出数据搭建DTW-ConvLSTM联合监控模型，并与常规统计模型和LSTM模型的预测结果进行比较。

4.1 联合监控模型所需数据集的构建

以连续6 d测值预测后续6 d测值，训练集时段选择2009年11月5日至2011年7月11日(测量频率1次/天)，为了得到尽可能多的可用数据，每隔1 d取一组训练数据，共560组(6天/组)，每组训练数据与前一组训练数据在时间维上相差1 d，存在5 d重复值；测试集时段选择2011年7月12日至2012年1月10日(测量频率1次/天)，每隔6 d取一组测试数据，共31组(6天/组)，测试数据间没有时间重叠。各测点监测时间不同时，通过插值进行规整。表1为某6 d模型输入矩阵L。输入模型前需将数据集按公式(10)分测点进行Max-Min标准化，使数值全部落在[0，1]区间。

表1 6天模型输入矩阵L

4.2 联合监控模型建立

4.2.1LSTM联合监控模型

采用Python软件深度学习框架keras，针对6×9大小的矩阵L搭建LSTM联合监控模型，网络优化方法为Adam，损失函数采用均方误差MSE，采用Dropout正则化方法，训练2000代；神经网络各层见表2。将28号坝段6个测点和3个环境量测点的监测数据输入LSTM模型。

表2 LSTM联合监控模型网络结构

4.2.2DTW-ConvLSTM联合监控模型

采用Python机器语言库PyTorch针对6×9大小的矩阵L搭建DTW-ConvLSTM联合监控模型；网络搭建方法见图4，其中ConvLSTM“细胞”包含一层卷积，特征数为20(即存在20个卷积核)，卷积核大小为3×3，零填充方式为相同卷积[10]；解码器卷积层的特征数为1，卷积核大小为1×1。网络优化方法为Adam，损失函数为均方误差MSE，学习率为0.001，训练300代。2.2节中，隐藏层维数b的值取5；已经说明矩阵L大小为6×9，故m=6，n=9。将28号坝段6个测点和3个环境量测点的监测数据输入搭建好的DTW-ConvLSTM模型。

4.3 统计模型建立

对28号坝段6个测点分别建立统计模型，建模时间为2009年11月5日至2011年7月11日(测量频率1次/天)，与联合监控模型的训练集时间相同。对扬压力测点，考虑上下游水位、周期温度、降雨量、时效影响因子，建模为公式(11)。对变形测点，考虑上游水位、周期温度、时效影响因子，建模为公式(12)。

各测点的模型复相关系数和回归系数见表3、4，表中的复相关系数R均大于0.8，各测点统计模型的拟合精度高。用得到的统计模型计算2011年7月12日至2012年1月10日(测量频率1次/天)的预测值，预测时间段与联合监控模型预测集相同。

公式(11)中：H为扬压水头的统计模型拟合值，m；Hh为上下游水位分量；HT为周期温度分量；Hp为降雨量分量；Hθ为时效分量；Hui、Hdi为监测日当天、监测日前1～4d、前5～10d、前11～20d、前21～30d的平均上游水位和平均下游水位(i =1～5)；Hu0i、Hd0i为计算时段第一天上述各时段对应的上下游水位平均值(i =1～5)；a1i、a2i为水位因子回归系数(i =1～5)；t0为计算时段第一天对应的t，t0=1；t为计算时段各天对应的t，为计算时段各天减去计算时段第一天所得分量；b1i、b2i为温度因子回归系数(i =1，2)；Pi为监测日当天降雨量、监测日前1d降雨量、监测日前2d降雨量、监测日前3、4两天降雨量均值、监测日前5～15d降雨量均值、监测日前16～30d的平均降雨量(i =1～6)；ci为降雨量因子回归系数(i =1～6)；θ=t/100；θ0=t0/100=1/100；d1、d2为时效分量回归系数。

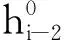
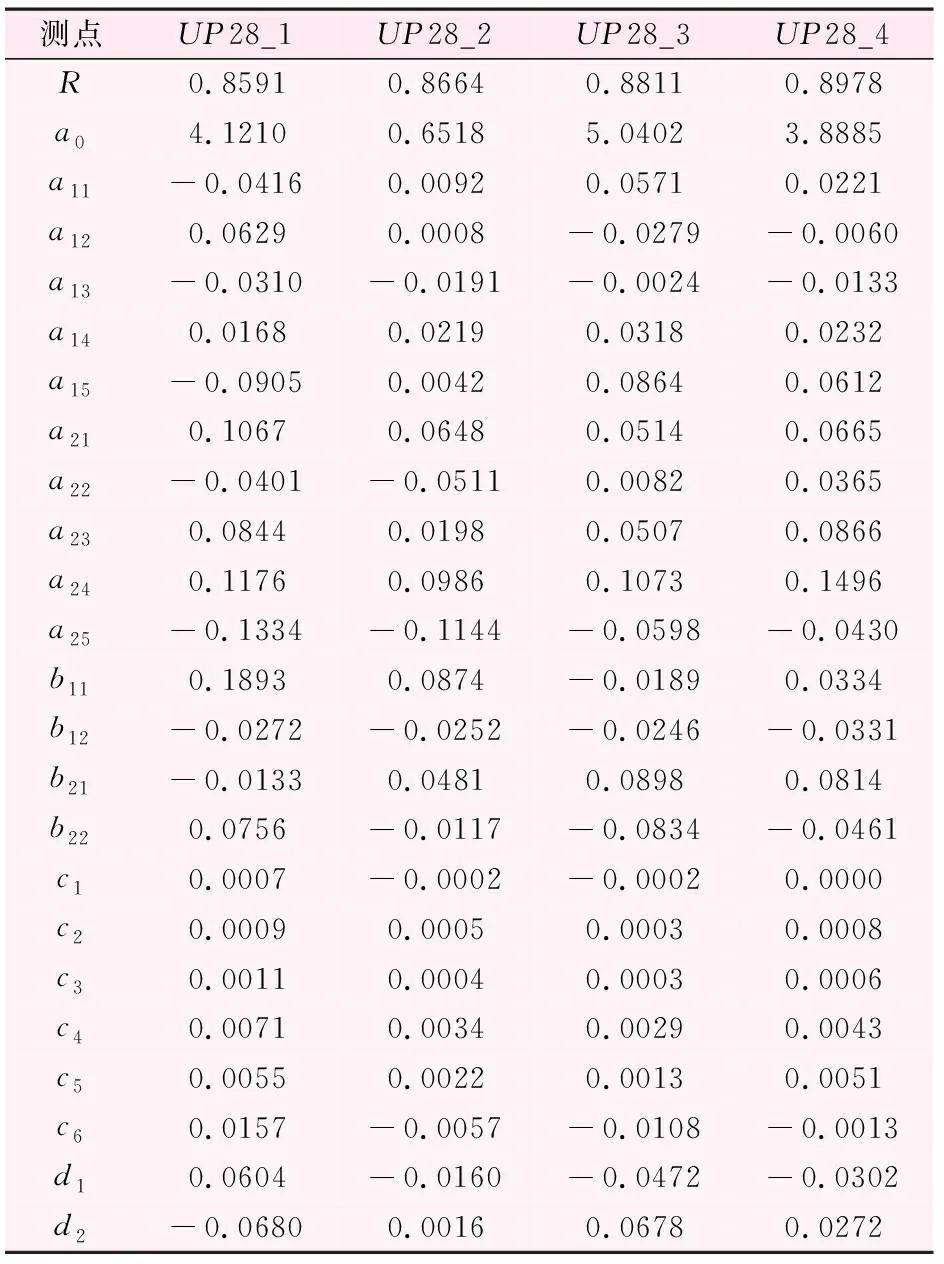
表3 扬压力测点复相关系数和回归系数

4.4 预测结果分析

3种模型的训练/拟合集、预测集完全一样，训练/拟合集为2009年11月5日至2011年7月11日，预测集为2011年7月12日至2012年1月10日，测量频率1次/天。以公式(13)的均方根误差(RMSE)评价模型性能，分别计算28号坝段6个测点LSTM模型、DTW-ConvLSTM模型和统计模型各测点预测值的RMSE，DTW-ConvLSTM模型预测值的RMSE比统计模型下降的百分比评价，结果见表5。

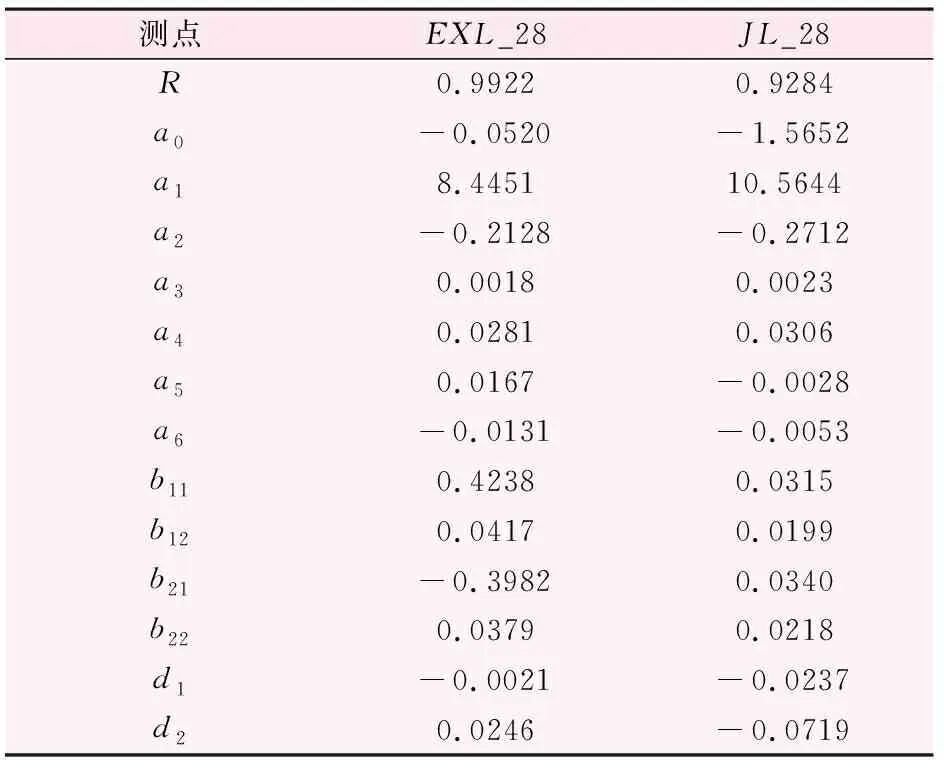
表4 变形测点复相关系数和回归系数

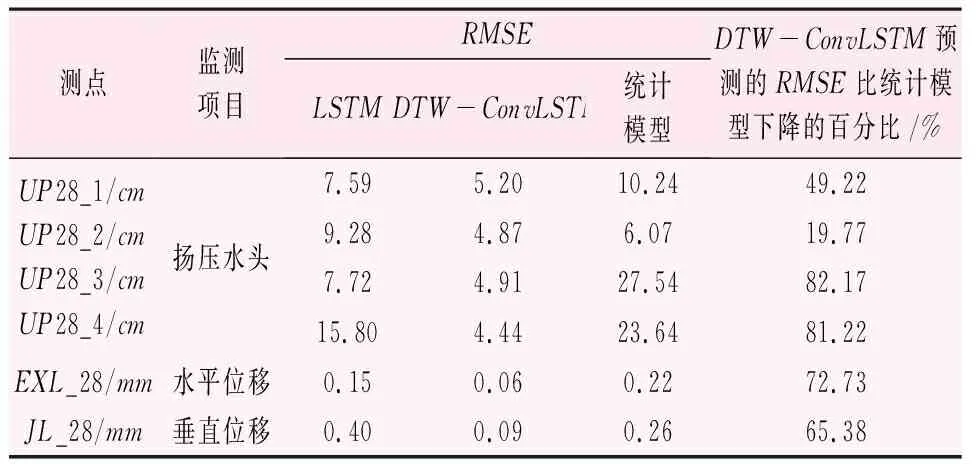
表5 模型预测性能量化评估结果

由表5可知：

(1) 28号坝段6个建模测点中，DTW-ConvLSTM模型预测值的RMSE在3种模型中最低，对扬压水头测点，数值在4.44～5.20cm之间，对变形测点，数值分别为0.06和0.09mm；除UP28_2和JL_28的4个建模测点中，统计模型预测值的RMSE最高。

(2) 对全部6个建模测点，DTW-ConvLSTM预测值的RMSE比统计模型预测值下降的百分比在19.77%～82.17%之间，有5个测点超过40%。

计算3种模型预测值和实测值之间的复相关系数R，如表6所示。该表反映出DTW-ConvLSTM模型预测值的R均大于0.8，远高于LSTM和统计模型。

绘制28号坝段6个测点实测值和3种模型预测值的过程线见图6。由图可知DTW-ConvLSTM模型的预测过程线始终与实测过程线最为接近；DTW-ConvLSTM模型掌握测值变化趋势的能力较强，在图6(e)中实测过程线在2011年10月15日至26日出现波动，DTW-ConvLSTM模型预测值出现了相同的波动，LSTM和统计模型没有预测到波动现象，在图6(f)中可明显察觉到DTW-ConvLSTM模型适应测值下降，LSTM和统计模型预测值没有减小，这一区别由DTW和卷积层导致；另外，DTW-ConvLSTM模型对UP28_1、UP28_2、UP28_3、UP28_4测点的预测效果明显好于统计模型。

综上所述：

图6 28号坝段预测值过程线

(1) 由于DTW算法和卷积层具有提取测点相关性信息的能力，且DTW算法对测点的相关性分析随训练集每组数据进入“ConvLSTM细胞”而实时更新，DTW-ConvLSTM模型适应测值变化趋势的能力强于LSTM模型和统计模型；

(2)DTW-ConvLSTM模型的预测精度高于统计模型的预测精度；

(3)DTW-ConvLSTM模型预测效果较好，具有实用性。

5 结 论

本文针对传统大坝安全监控模型仅能对相同监测项目测点进行单测点或多测点建模的不足，通过分析卷积神经网络(CNN)，长短时记忆神经网络(LSTM)和动态时间规整算法(DTW)的特点，提出了大坝安全监测信息联合建模方法，主要研究成果如下：

(1) 分析了传统大坝安全监控模型限于同项目建模的不足，阐述了长短时记忆神经网络(LSTM)、卷积神经网络(CNN)和卷积长短时记忆网络(ConvLSTM)的建模原理，结合动态时间规整算法(DTW)，提出了卷积长短时记忆网络模型改进方法。

(2) 采用编码-解码结构形式，构建了DTW-ConvLSTM多项目测点联合监控模型，给出了模型输入和输出数据结构，编写了DTW-ConvLSTM模型训练过程伪代码，基于Python开发了相关程序。

(3) 实例分析表明，联合监控模型可以实现多监测项目多测点的同时监控。DTW-ConvLSTM模型适应测值变化趋势，精度明显高于LSTM模型和常规统计模型。可为大坝安全监控及预警的可靠性提供保障。