提高二维工作台定位精度的误差补偿方法研究

徐品烈，田利忠，种宝春，常 亮，赵玉民，孙莉莉

(1. 中国电子科技集团公司第四十五研究所， 北京100176；2. 中国电科电子装备集团有限公司， 北京100176)

二维工作台是半导体专用设备中最常见的结构部件。它的主要功能是实现加工件的传输和定位。近年来，随着设备性能提高，对二维工作台的定位精度提出了更高的要求。使用较低的硬件成本构建工作台来满足更高的定位精度是设备制造工程师设计中面临的一个问题。

用误差补偿的方式提高工作台的定位精度是一种简洁有效的方法，许多文章讨论了采用激光干涉仪，单独测出工作台直线轴的定位误差分布，对误差采用不同的分析方法，采用软件对控制器发送的XY 的定位指令单独进行误差补偿，提高定位精度。这种方法可以有效地减小误差，但对XY 轴单独测量，分析计算过程中也未考虑XY 互相影响造成的定位误差。本文提出了单独测量XY 轴的直线度误差、垂直度误差、定位误差，并分析每根轴的每项误差对单轴定位精度和关联轴定位精度的影响，建立关联函数予以误差补偿，并实验验证，证明了此方法可有效提高二维工作台定位精度，并为同类二维工作台今后的设计提供参考。

1 系统硬件结构

图1 为二维工作台结构图，主要由直线导轨副、直线电机、光栅尺、基座平台、支撑件等组成。采用直线电机作为驱动机构，避免传动误差，部件动态性能好，有效地降低装配误差，为达到较高的定位精度打下了良好的硬件基础。

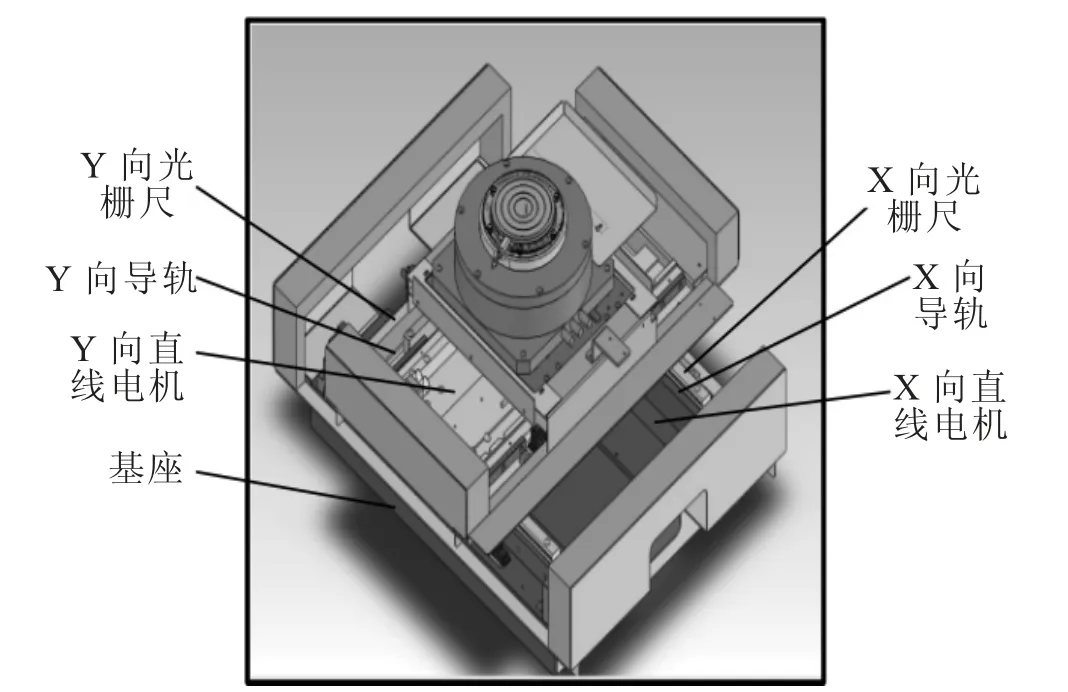
图1 2D 工作台结构图

设计中，要求XY 整个行程范围内，从任意一点A 到目标点B，在B 点的XY 两个方向的定位精度均要求达到±3 μm。

二维工作台机构由直线电机加直线导轨副组成，由伺服系统驱动，采用光栅尺进行位置反馈，组成了一个全闭环的控制系统。X、Y 轴有效工作行程均为200 mm，最大移动速度为400 mm/s，最大移动加速度10 000 mm/s2，重复定位精度±1 μm，定位精度±3 μm。工作台采用双零级精密大理石为底座。

2 误差来源分析

二维工作台的误差来源比较复杂，主要包含关键零部件精度、制造加工过程和检测3 个方面：

（1）工作台底座、滚珠丝杆、螺母副、导轨、光栅尺等工作台零部件在制造过程中引入的尺寸误差及装配过程中引入的装配误差；

（2）工作台在负载下的变形及工作台结构的力变形引起的定位误差；

（3）具体工况中振动、湿度、温度、气流等因素引起的环境误差及检测误差等[1]。

由于二维工作台是在恒温恒湿工作环境下运行，环境因素基本不变，所以主要的误差来源是装配误差和制造误差，由于这2 项误差在产生之后基本保持恒定值，因此选择使用双频激光干涉仪先单独测得二维工作台的单轴各项误差分布曲线，然后选择一种方法对误差曲线进行分割，再分析每项误差对单轴和关联轴的精度的影响，建立函数关系，再通过软件根据工作台不同的行程区间进行分段补偿，以达到控制工作台误差的目的。

3 误差的处理方法

影响定位精度的每种误差在行程范围内是非线性的，直接建立误差曲线是比较困难的，但是将误差曲线分段，在小的区域范围内可以线性化处理[2]。为了将误差控制在许可的范围内，采用的方法是XY二维平面工作台，对每个轴在全行程范围内，对每隔一定长度取一个采样点，假设采样点长度间隔为n，共计K个采样点，这样，X 轴行程可以分割为长度为n的k个线段，同理，Y 轴行程可以分割为长度为n的k个线段，这样XY 工作台行程内的平面分成n×n个小的区域，如图2 所示。

在这个平面上，从A 点运动到B 点，目标点B(x，y)在一个小的区域内。依据B 点的坐标值x、y，可以单独计算出B 点在X 轴的段号和Y 轴的段号。依据B 点的x坐标，计算出B 点在X 轴的第m段，第m段两个测量点对应的X 轴坐标为xm、xm+1，这两个测量点对应的误差为△Em和△Em+1，如图2 所示，在这个区域内，误差可用线性差值的方法求出，那么，B 点在X 轴对应的误差△Ex=[（x-n·m）/n]·(△Em+1-△Em)。

图2 XY 平面分割图

图3 区域误差分布图

使用双频激光干涉仪作为测量工具，首先分别测出X 轴、Y 轴在采样点直线度误差、垂直度误差、定位误差，将单轴的每种误差建立独立的数据表格，将这三种误差综合，作为2D 平面上目标点的误差，在软件中加以补偿，实现了工作台精度提升[3]。

4 误差补偿方法

4.1 直线度误差的处理方法

在X 轴上，B 点前后节点号分别为m，m+1，那么，X 轴的直线度误差记△El，为前后节点的直线度误差即为△Em，△Em+1，可以用线性查补的方法求出X 点的直线度误差△El[4]：

X 轴的直线度误差△El对B 点在X 方向定位造成误差△El·（1-cos β），对B 点在Y 方向造成误差△El。同理，Y 轴的直线度误差△E'l对B 点在X 方向定位造成误差△E'l，对B 点在Y 方向造成误差△E'l·（1-cos β）。

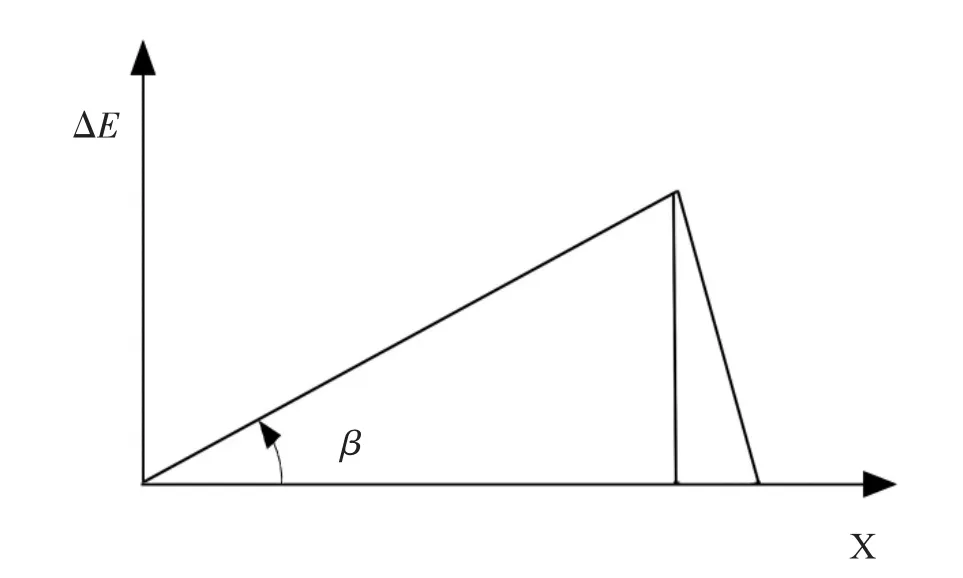
图4 误差计算图

4.2 垂直度误差

垂直度误差分布与消除方法与直线度误差方法一致，区别在于因为X 轴做基准轴，那么只考虑Y 轴误差对定位精度的影响。

Y 轴垂直度误差记为△Eo，

垂直度误差对B 点在X 方向定位造成误差△Eo

Y 定位造成误差△Eo·（1-cos β）

4.3 单轴定位精度对平面定位精度的影响

单个运动轴的定位精度，其对定位中单个轴的定位精度影响是直接的，在总误差中可直接计算。

X 轴的定位误差为△Epx，

Y 轴的定位误差为△Epy，

经以上分析，目标点B 点的总误差为△E，可以分解为△Ex和△Ey。

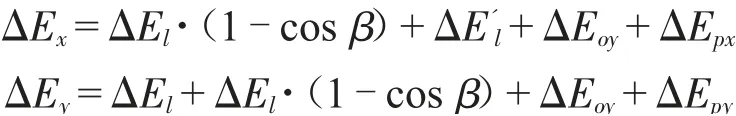
求出总误差后，在软件中做定位误差补偿算法，根据B 点的实际坐标，控制器发送运动指令时，对误差进行补偿。

5 实验验证

实际测试时，使用的测试平台X、Y 轴有效工作行程均为240 mm，最大移动速度为400 mm/s，最大移动加速度10 000 mm/s2。每5 mm 取一个采样点，每轴均采49 个样点。每组测量重复最少5次。然后求平均值作为测量值。

图5 和图6 是直线度误差生成的图形。

图5 X 轴直线度误差

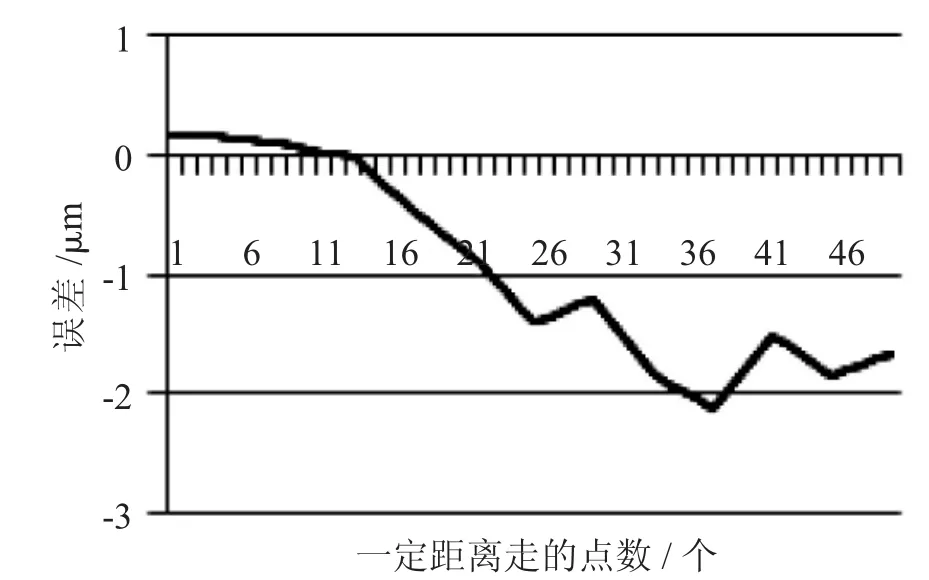
图6 Y 轴垂直度误差

从图5 可以看出，通过精确调试，X 轴的直线度误差可以控制在1 μm 以下。垂直度误差也通过边测量边调试的方法控制在1 μm 内。Y 向垂直度误差在2.5 μm 内。

图7 是X 轴定位精度单独测量时的数据生成图。XY 轴的定位误差单独测量时都达到15 μm。

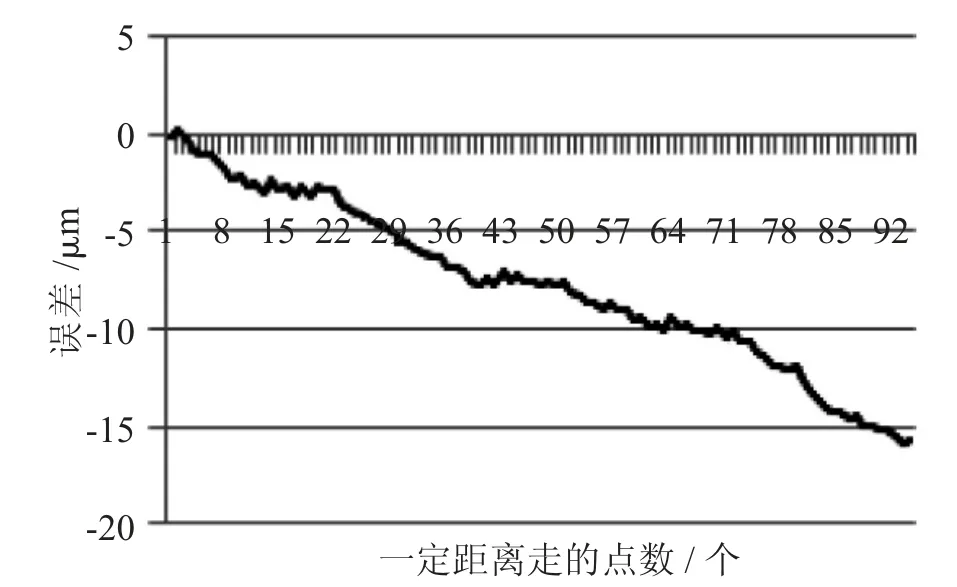
图7 X 轴定位误差

经过误差补偿后，测量结果如图8 所示，可用二维光栅测量仪或者激光干涉仪加视觉传感器同时测量二维平面内的XY 的定位精度，实际结果定位精度满足设计要求。

图8 XY 轴的定位精度

根据实验数据，2D 工作台在行程范围内移动时，在任意一点的定位精度优于3 μm，满足设计要求，用误差补偿的方法可以达到较高的定位精度。

6 结束语

本文讨论了测量二维工作台XY 轴直线度误差、垂直度误差、定位精度误差等，分析了每种误差对单轴定位精度和关联轴定位精度的影响，采用水平分割法对误差线性拟合，建立了误差补偿的函数方程式，用误差补偿的方法，提高了二维工作台的平面定位精度，并为定位精度的计算方法提供了参考。