喷砂冲蚀实验中颗粒轨迹的数值预测*

张晴波，郭 涛,2，洪国军，曹 蕾

（1. 中交疏浚技术装备国家工程研究中心有限公司，上海 201208；2. 上海交通大学船舶海洋与建筑工程学院，上海 200240）

冲蚀指固体颗粒输送时不断碰撞壁面并移除材料的现象，会严重损害设备的寿命或功能，增加生产成本。平板冲击实验是冲蚀研究的重要手段，实验中颗粒的运动轨迹复杂多变，难以准确记录每次撞击的位置、速度与粒子大小，常用概率分布的方式近似处理。近年来数值技术发展迅速，已用于设备的冲蚀破坏预测[1-3]。从冲蚀研究的角度出发，准确预测每个粒子的速度和位置代价高昂，注重群体轨迹分布的宏观数值求解更容易实现，并可有效地替代给定概率分布的颗粒轨迹[2,4-5]。但是，具体问题中的耦合作用差异明显[6]，受制于近声速气流、不规则粒子与粗糙壁面之间的复杂耦合作用，目前喷枪喷射粒子群体的轨迹仍难以有效预测。为此，本文通过实验宏观统计了喷枪喷射海砂的颗粒速度与冲击位置分布，选用合适模型以实现喷射砂粒群运动轨迹的数值预测。

1 平板冲击实验

为考察某填海造地工程中从海底挖取的天然海砂对输送管路的磨损能力，实验中海砂经负压喷枪喷射后以不同角度不断冲击Q235 钢（管路材料）平板，考察海砂对输送装备的冲蚀性能，并统计测量了海砂的碰撞速度与撞击位置。工程中海砂的粒径集中在75～5 000 µm 范围内，中值粒径约为780 µm；使用圆孔筛网选出粒径在500～2 000 µm 内的主要部分作为实验砂。

实验前，使用扫描电子显微镜(scanning electronic microscopy, SEM)观察海砂样品，发现其外形较粗糙，呈纺锤状或块状，球形度介于立方体与四面体之间。由于海砂粒径、形状、成分个体差异明显，少量颗粒的实验结果无法保证研究的普适性，以颗粒群体为研究对象更有意义，因此单次冲击板材的砂质量为10 kg。

实验方案如图1 所示：空压机提供的压缩空气经除水后进入喷枪加速，在喷枪侧向进口形成负压；空气-海砂混合物在压差作用下被吸入侧向进口，随后从喷枪的出口管中以较高速度锥状喷出，冲击Q235 钢制平板试块并造成冲蚀磨损，期间产生的烟雾被抽风机吸入收尘袋。实验中，调节进气压力可改变气-砂混合物的喷射速度，调整试块板的安装角度可改变冲击角度，喷砂后拍摄冲击痕迹，并用精密电子天平称量试块的质量损失，重复3～4 次取均值。实验发现：Q235 钢试块在90°冲击角下的磨损量最小，在45°～60°冲击角下磨损量最大，约是前者的1.3 倍。

图1 气驱砂冲蚀磨损实验装置示意图Fig. 1 Diagram of the air-blasting-sand erosion experimental setup

为测量不同进气压力下海砂撞击试块的速度，使用了图2 所示的砂速测量装置：通过隔板以及旋转圆盘上径向细长缝隙的喷射砂束的周向速度分量很小，飞行L 距离后击打在与圆盘同轴同速旋转的无碳复写纸盘上。由于电机旋转角速度ωdisc恒定，可根据式(1)估算砂粒的冲击速度v 为：

图2 喷砂测速装置示意图Fig. 2 Speed test device for blasting sand

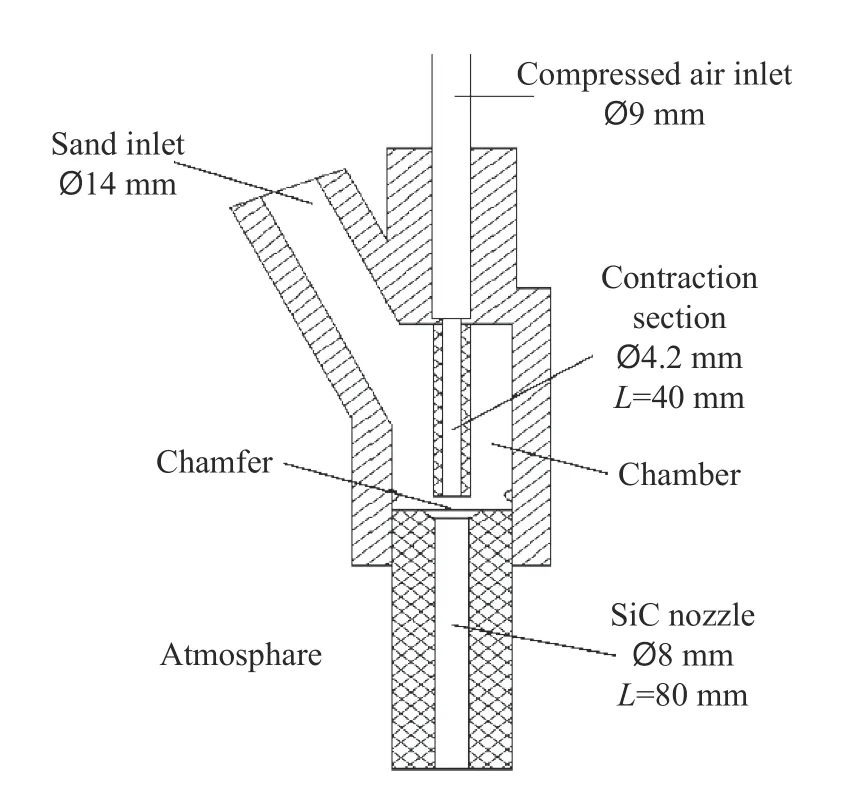
图3 喷枪内部结构示意图Fig. 3 Structure diagram of the sand-blasting gun

式中：ϕ为纸盘上的击打痕迹与圆盘缝隙之间偏转角度。

2 数值方法

为实现海砂喷射轨迹的数值预测，按图3 中的喷枪结构建立三维几何模型，使用商用数值软件ANSYS Fluent 对空气与海砂在喷枪内外的双向耦合过程进行双精度稳态数值求解。使用离散相模型(discrete phase model, DPM)来预测砂粒的轨迹，即在欧拉参考系下计算气体流动，在拉格朗日参考系下计算砂粒运动，并通过双向动量传递实现相间耦合作用。通常DPM 在固粒体积分数小于10%时的预测结果较为可靠，实验时10 kg 的海砂全部喷出大致需要5 min，喷砂的速度在20 m/s 以上，体积流率约为1.3×10−5m3/s，此时砂粒在喷嘴出口附近的体积分数不超过1.3%，DPM 完全适用。

计算域内网格总数约180 万，壁面首层网格厚度5×10−5m。重力方向竖直向下，压力、密度为相对真空环境的绝对数值，环境与喷枪壁面恒温20 ℃。参照实验设定喷枪进气口的总压边界，进砂口设置为0.1 MPa 总压进口，喷嘴出口为0.1 MPa 静压边界，使用k-ω 湍流模型。砂粒径均取中值粒径，密度2 600 kg/m3，进砂质量流率为0.0333 kg/s；追踪粒子时引入随机行走模型，即在两相动量耦合时气体速度考虑湍流脉动，使单个粒子的轨迹具有多种可能性，轨迹总数为26 200，单个轨迹的质量流率与入射单元的进口面积成正比；使用均化技术使颗粒源项在流体域内的分布平滑过渡，以减少数值解的网格相关性。计算中还引入一些合理简化以降低计算成本：仅考虑碰撞壁面后砂粒反弹而忽略可能发生的破碎；假定空气为单一组分的理想气体而忽略可能残余的细小冷凝水滴，根据理想气体假设和Lennard-Jones 势能理论计算其物理性质；忽略气-粒之间的传热作用。

2.1 流体控制方程

流体域的连续方程和能量方程与考虑壁面传热的单相可压缩流动相同，不再赘述。动量方程考虑离散颗粒影响：

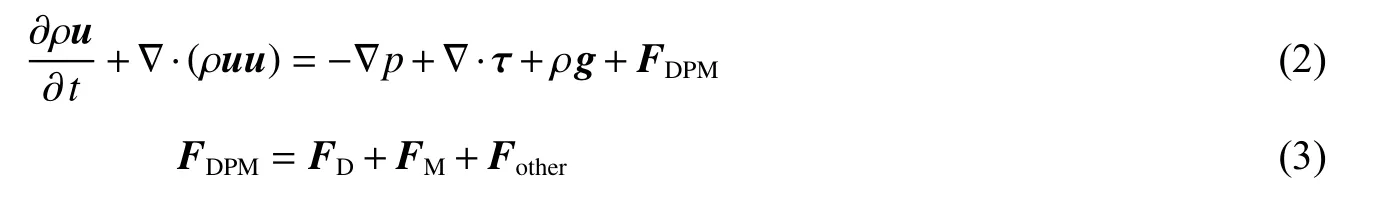
式中：ρ 为气体密度，u 为气体速度，τ 为应力张量，g 为重力加速度，FDPM为离散的砂粒对单位质量气相的作用力，FD为砂粒对气体的反曳力，FM为Magnus 升力的反作用力；Fother为其他的粒子附加力，如虚拟质量力等，计算中因空气密度相对较小而忽略。

2.2 粒子追踪方程

忽略其他附加力时，粒子运动满足动量方程常微分方程：

式中：up为粒子速度，fD为曳力提供给粒子的加速度，fM为Magnus 升力提供给粒子的加速度，ρp为颗粒密度，d 为颗粒径，CD为曳力系数，Re 为颗粒雷诺数。

砂粒的旋转运动对其运动轨迹具有明显影响，粒子的角动量方程常微分方程为：

3 数值模型与结果分析

数值计算时，按实验条件改变喷枪进气端上游的压力，编译自定义函数来设置耦合模型并统计颗粒平均碰撞速度；为了统计颗粒碰撞位置，使用Oka 等[7]提出的砂冲击结构钢公式计算冲蚀。将实验的冲蚀磨损痕迹和砂粒碰撞速度与不同模型下的数值解进行比较，以确定合适的喷砂气-固耦合模型。本节的数值比较工作是同时进行的，用于对比的数值结果中未明确的模型均为最终选择的模型。

3.1 非球形高Ma曳力模型

曳力是促使相对运动的两相速度趋同的阻力，通常是颗粒输送中最重要的相间作用力。本次实验中，砂粒形状不规则，空气在喷嘴结构内跨音速流动，Re 主要分布在1.5×102～ 1.5×104范围内，曳力模型应尽量满足该条件。

当空气的可压缩性不可忽略时，相对流动马赫数Ma 也会明显影响曳力[8]，Loth[9]认为气体与球形粒子的相对速度达到Ma＞0.6 以上时，绕流会达到音速，在粒子前形成弓形激波并产生流动分离现象，导致CD大幅增长。考虑颗粒形状因素对曳力影响的曳力模型通常来自实验研究，海砂的形状不规则且多变，尚无有效手段来表征其真实曳力系数，本文参考了利用球形度φ (等体积圆球与真实颗粒的表面积比)来表征形状因素影响的非球形颗粒曳力模型[10]，其在本文实验的Re 范围内，粒子的φ 越小则CD越大且越趋向于常数。数值计算发现，高Ma 的圆球曳力模型[9]或非球形曳力模型[10]下的粒子速度结果均无法匹配实验条件下的平均砂粒撞壁速度。可能是真实气-粒耦合作用同时受到了砂粒形状不规则以及高Ma 时可压缩空气的影响，而上述模型仅各自考虑了其中一个方面。经多次测试，本文提出一种针对实验条件的非球形高Ma 数模型：形状不规则的海砂受曳力明显大于球形粒子，设其平均球形度为0.74。这既符合海砂球形度介于立方体与四面体之间的SEM 观察结果，也使得低Ma 条件下平均砂速的数值解与实验结果相吻合；相对高流速时海砂表面更容易产生流动分离而进一步增大阻力，即临界Ma 更小，因此假定砂颗粒的临界Ma 减小至为0.2，CD与Ma 正相关强度为球形颗粒的1.5 倍；且认为CD受Ma 影响的幅值比等同于球形颗粒，约为2.2，那么海砂的CD在实验的Re 范围内可简化为：

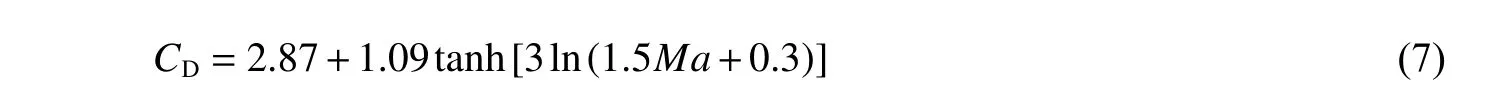
本文使用该式计算海砂在喷枪内受高速空气拖曳增速过程中的CD。

图4 不同曳力模型得到的平均喷砂速度与实验值比较Fig. 4 Comparison of blasting sand speeds between numerical and experimental results

图4 为分别使用式(7)的非球形高Ma 模型、球形高Ma 模型[9]及非球形模型[10]3 种曳力得到的碰撞速度的平均数值解与实验值的比较。图中，随着喷枪进气压力从0.1 MPa 提高到0.34 MPa，实验的平均碰撞速度在近似线性增加的同时，速度分布范围也有明显增加，这应是真实砂粒的形状、大小不一造成的。非球形模型在进气压力较低(0.1～0.2 MPa)时得到了符合实验的砂速数值结果，但在更高压力时砂速偏小，至0.34 MPa 时偏差达17%，这是该模型忽略了喷枪内相对流速较高时可压缩气体流动分离对CD变化的影响。圆球高Ma 模型得到的砂速也随进气压力增大而提升，但各值均明显小于实验值，这是因为该模型忽略了颗粒形状对CD的显著影响，CD过小导致数值解偏差最大。本文提出的非球形高Ma 曳力模型在不同进气压力下均得到了与实验结果吻合的平均砂速，证实了其有效性。

3.2 粗糙壁面与Magnus 升力模型

为考察壁面反射与Magnus 升力模型对砂粒宏观轨迹的影响程度，图5 给出了进气压力为0.34 MPa的喷枪90°垂直喷砂冲击试块，选用光滑壁面等角反射(速度恢复系数取0.8)、忽略Magnus 升力的模型得到的冲蚀率结果与相同条件下实验试块的冲蚀痕迹比较。图5(a)中，海砂冲蚀钢板后形成直径约60 mm的圆形凹坑，由内向外逐渐变浅直至不再连续，并有距离中心越远越稀疏的许多点状痕迹；而数值结果是图5(b)中直径约25 mm 的类圆形痕迹，冲蚀面积与实验差异很大且没有分散冲蚀点。可见该模型过于简化，无法求得喷射砂粒的合理轨迹及撞击位置。

图5 实验冲蚀痕迹与光滑壁面且忽略升力的数值结果对比Fig. 5 Comparison between experimental and numerical results (smooth wall & no lift force).

图6 粗糙壁面模型对冲蚀数值结果的影响Fig. 6 The rough wall model effects on numerical erosion results

高雷诺数下，Magnus 升力提供给砂粒的加速度可表示为：

式中：CL为旋转升力系数，由实验确定。经比较，本文最终选用了 ∆γ为20°的粗糙壁面模型与Oesterlé等[13]提出的升力模型，后者满足：

式中：Reω为旋转雷诺数。图7 给出了相同条件下，联合非球形高Ma 曳力、粗糙壁面与升力模型耦合求解的气相速度与部分砂粒运动轨迹结果。图7(a)为中截面的流场速度分布图，其中压缩空气在喷枪喉管末端附近降温降压，流速峰值达400 m/s 以上，为典型跨音速流动；图7(b)随机显示了少量砂粒撞击Q235 板之前的轨迹线，可见砂粒从喷嘴射出后将按不同角度扩散，扩散角度越大，颗粒越少。

图8 为联合模型求解的砂粒垂直冲击Q235 钢试块的冲蚀率，与图6(d)相比，应用Oesterle-Bui 升力模型后冲蚀的范围明显增大，且有明显的环状“浅晕”区域以及离散冲蚀点，与图5(a)的实验冲蚀痕迹在外观、大小上都比较相近。图8 的数值结果与实验结果吻合较好，说明在喷枪喷砂轨迹的气-砂耦合数值模拟中，选择合适的模型及相应参数是非常必要的。

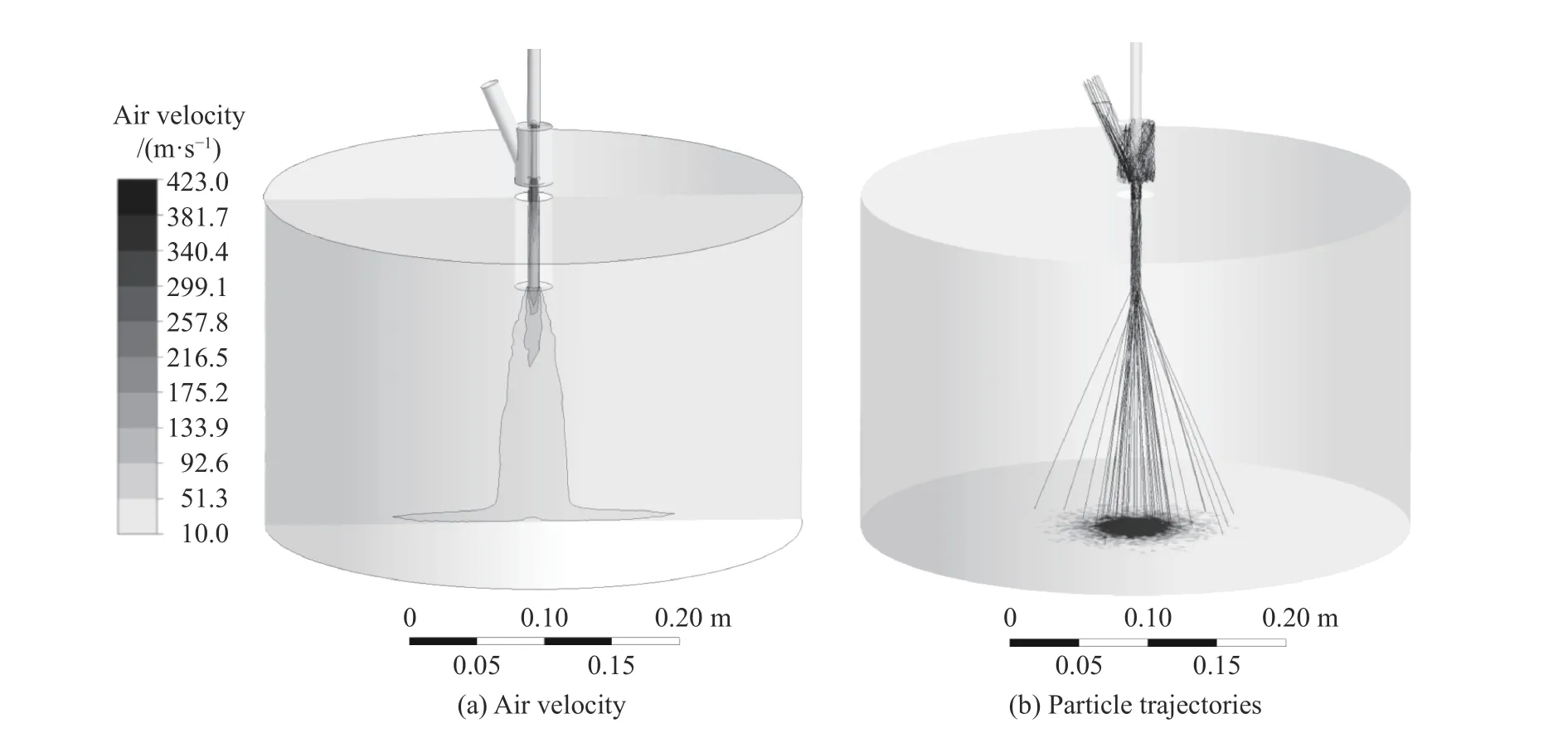
图7 非球形高Ma 曳力，粗糙壁面与升力的联合模型下的气相速率度与部分颗粒轨迹数值解Fig. 7 The numerical results of air velocity magnitude and some particle trajectories by the combined model

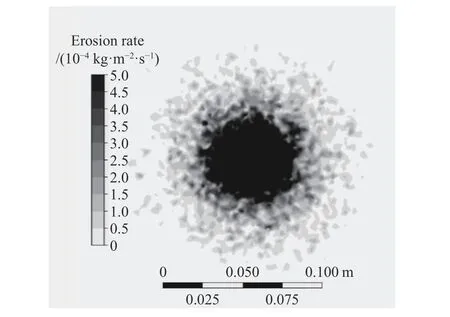
图8 联合模型求解的砂粒对试块的冲蚀率Fig. 8 The numerical result of the erosion rate by the combined model

4 结 论

粒径不一、形状不规则的颗粒群被近声速气体携带时的耦合作用尚无有效的通用模型。本文在冲蚀磨损实验中测量了不同进气压力下喷枪喷射海砂的速度和碰撞位置，通过数值方法实现了砂粒运动轨迹的宏观预测，主要结论有：

（1）本文发展的非球形高Ma 曳力模型同时考虑了颗粒形状和相对高Ma 流动中空气可压缩性的影响，可以较准确地预测实验中的砂粒碰撞速度。

（2）砂粒轨迹预测需慎重选择曳力、旋转升力与壁面反射等具体耦合模型，联合应用非球形高Ma曳力、∆γ为20°的粗糙壁面以及Oesterle-Bui 升力模型后，数值解在撞击速度和撞击位置上均与实验结果契合良好。

后续工作中将进一步研究真实粒径分布、冲蚀公式以及磨损累积效应对冲蚀磨损的影响，以期实现喷砂冲蚀磨损的准确预测。