Q420 钢管大气腐蚀后的抗侧撞性能*

旷金鑫，张春涛,2，郝志明，李洪祥

（1. 西南科技大学土木工程与建筑学院，四川 绵阳 621010；2. 西南科技大学土木工程与建筑学院工程材料与结构冲击振动四川省重点实验室，四川 绵阳 621010；3. 中国工程物理研究院总体工程研究所，四川 绵阳 621999）

圆形钢管广泛应用于修建桥梁、工业厂房和高层建筑等大型钢结构建（构）筑物。腐（锈）蚀一直是钢结构应用过程中不容忽略的因素，服役于山区的钢结构桥梁、井架、塔体和厂房等建（构）筑物在遭受大气环境腐蚀的同时，还可能承受车辆、山体滑坡、泥石流和落石等的撞击作用。因此，开展腐蚀损伤钢结构的抗冲击性能研究，对评估结构寿命、保证其安全服役等都具有重要意义。

针对质量体横向撞击圆柱壳体构件的动力响应过程，Jones 等[1]、茹重庆等[2]、程国强等[3]建立了相应的力学模型。目前，多采用重力式落锤试验和有限元模拟的方法，对比不同撞击参数的响应规律，以开展构件抗冲击研究。Zhang 等[4]通过试验研究了弹体形状及圆钢管尺寸对撞击变形破坏模式的影响。朱翔等[5]利用重力落锤试验研究了钢骨混凝土构件的冲击响应规律及冲击速度、冲击能量等因素对结果的影响。郝志明等[6]采用数值计算与试验结合的方法分析了20 钢梁受侧向冲击的剪切破坏行为。Yousuf 等[7]根据试验与仿真结果对比了空心和内填混凝土的低碳钢管柱在冲击载荷作用下的性能。

对于受腐蚀钢构件的数值建模，有两种定义腐蚀损伤的方法。一种是考虑大气腐蚀产生蚀坑造成有效截面减少，采用削弱构件厚度构造腐蚀缺陷的方法[8-11]建立预腐蚀后的构件模型；另一种是将大气腐蚀损伤表示为钢材材料力学性能参数的折减[12-13]。Kachanov[14]、Rabotnov[15]通过引入损伤因子对存在离散缺陷材料的拉伸力学性能进行了表征。史炜洲等[16]、郑山锁等[17]则通过加速腐蚀试验获得了Q235B 钢材的失重率对其力学性能参数的折减规律。

本文中，基于一维损伤理论建立低合金钢材的腐蚀损伤本构模型，并通过加速腐蚀试验获得Q420 钢材的大气腐蚀本构关系预测曲线，借此建立考虑腐蚀削弱的Q420 钢管数值模型，采用改变冲击条件参数的方法对比分析冲击条件对构件动力响应规律的影响，并与不同腐蚀程度的Q420 钢管恒轴力落锤试验结果进行对比，以验证数值模型的有效性。

1 低合金钢大气腐蚀损伤本构模型

针对大气腐蚀的钢材损伤问题，可根据一维损伤理论[14]，引入损伤因子ω 对材料性能进行名义折减，弹性阶段仍符合胡克定律：

式中：σ 为材料应力，ε 为总应变（在材料弹性阶段即为弹性应变），E0为材料弹性模量。

塑性流动阶段的本构模型可采用Voce[18]对上升段的经典描述：

式中：σ0为饱和应力（即无腐蚀损伤材料极限抗拉强度），εp为流塑应变，α、β 为材料参数。

一维损伤理论假定本质上是考虑尺寸效应的影响，将大气腐蚀造成的损伤视为材料性能参数的折减，而不考虑试件几何尺寸的变化，根据质量与体积之间的物理关系，引入等效密度ρe来表征材料的质量损失，表示为：

式中：m 为试件初始质量，D 为腐蚀损失质量，V 为试件原始体积。

低合金钢材在自然大气中的腐蚀损伤程度d 表示为：

将式(2)右端第一项移至左端，两端同时取对数得：

令：

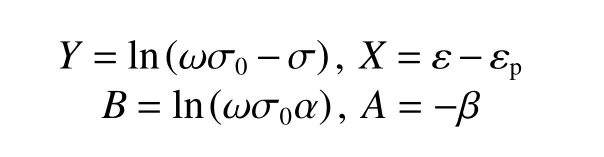
对腐蚀损伤后的钢材试件开展静力拉伸试验，将弹性阶段的应力(σ(d))、应变(ε(d))的结果代入式(1)进行线性拟合，所得直线斜率与无腐蚀损伤试件结果拟合的斜率之比即为相应腐蚀程度下的损伤因子ω(d)，然后将弹塑性阶段的应力σ(d)、应变ε(d)及损伤因子ω(d)代入式(5)，则有：

式中：

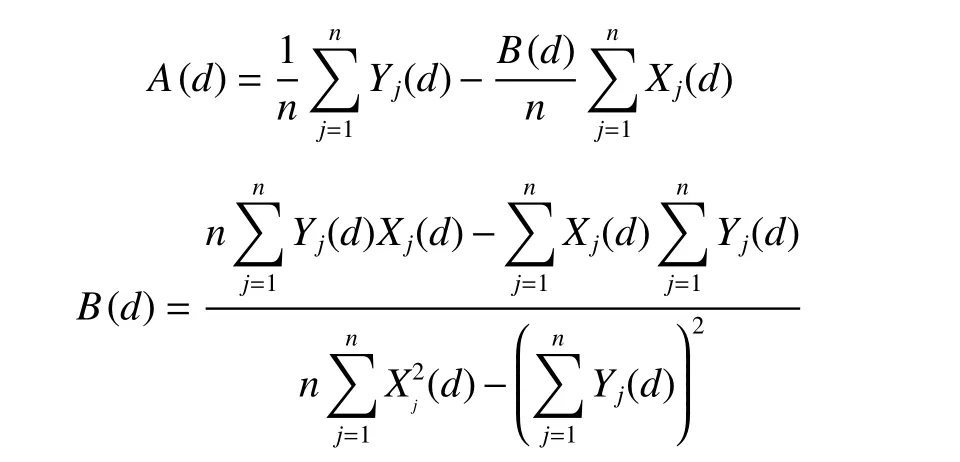
通过上述方法获得不同腐蚀程度的低合金钢材料参数α、β，并进行参数非线性回归获得关于腐蚀损伤量d 的参数表达式α(d)、β(d)，再代入式(1)、式(2)，即可得到含有腐蚀损伤的材料本构方程：

2 试验研究

2.1 加速腐蚀试验及相关材料性能测试

根据GB/T 228.1—2010《金属材料—拉伸试验 第1 部分：室温试验方法》[19]对材性试件制备的规定，对同批次钢管试件进行局部裁切，制成纵向弧形截面静力拉伸试件，试件尺寸设计见图1。采用万能材料性能试验机，对材料的静力拉伸性能进行测试。加载方式采用位移控制，加载速率为2 mm/min，通过50 mm 引伸计和应变片测得应力应变关系。

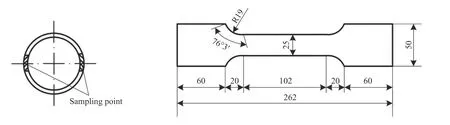
图1 材性试件设计（单位：mm）Fig. 1 Material test piece design (unit: mm)

2.2 重力式落锤试验

本次试验通过自主设计的重力式落锤冲击系统开展，冲击试验整体装置如图2 所示。该装置左右两端以门形反力钢架作为支撑，右端的加载系统可对试件施加轴向压力，冲击落锤选用40Cr 模具钢制倒梯形平头落锤。装置竖向高度8 m，最大落锤质量200 kg，通过改变下落高度和砝码质量，实现不同工况下的试验。

图2 重力式落锤冲击试验装置Fig. 2 Gravity drop hammer impact test device

冲击试验在恒轴力条件下进行，不考虑轴压对结果的影响。轴压比取0.2，对应的轴力为116.92 kN，落锤质量为54.70 kg，具体试验工况如表1 所示。通过L1600E 冲击力传感器、BFH120-3AA 应变片、MEMRECAM HX-4E 高速摄像机等仪器传输瞬态信号，由DH5960 超动态采集仪对电信号进行采集处理，获得瞬态时程数据，试件边界条件为一端固支一端滑动铰支，如图3 所示。

表1 落锤试验工况Table 1 Drop hammer test conditions

2.3 试验现象及结果

2.3.1 加速腐蚀试验结果

不同腐蚀程度的试件表面如图4 所示，腐蚀导致试件初始缺陷放大并产生新缺陷，具体表现为试件蚀坑的发展、增加，随着腐蚀程度的加深，试件表面蚀坑增多。静力拉伸试验结果如表2 所示，考虑试件腐蚀削弱效应的影响，材料的名义屈服强度和名义极限抗拉强度明显下降，当腐蚀程度达到40%时，试件的名义屈服强度仅为原试件的61.91%，伸长率仅为未腐蚀时的54.86%。

对静力拉伸试验结果按照第1 节的方法进行回归，并将获得的参数方程代入式(7)，得到Q420 低合金钢材加速腐蚀后的本构方程，表达式为：

图3 试件边界条件示意图Fig. 3 Schematic diagram of boundary conditions of specimens

图4 不同腐蚀程度的试件表面Fig. 4 Specimen surface with different degrees of corrosion

由于弹性阶段的应力σ 与应变ε 呈线性关系，此处仅给出材料塑性流动状态上升阶段（ε≥0.002）的变化趋势，如图5 所示。从图5 中曲线的整体趋势来看，损伤因子随腐蚀程度的增加而增大，材料的屈服强度和极限抗拉强度呈下降趋势。由表3 可知，本构模型预测值与试验值之间的最大误差为8.02%，屈服强度和极限强度对应的和方差分别为0.001 5 和0.011 0，预测结果较好。

表2 静力拉伸材料力学性能Table 2 Static tensile properties of mechanical properties

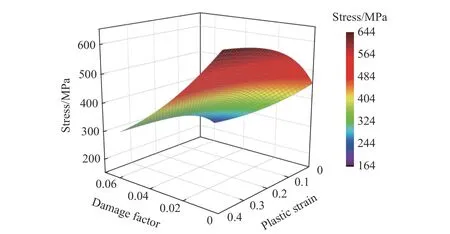
图5 计及腐蚀损伤的Q420 低合金钢材本构曲线Fig. 5 Constitutive curve of Q420 low alloy steel considering corrosion damage

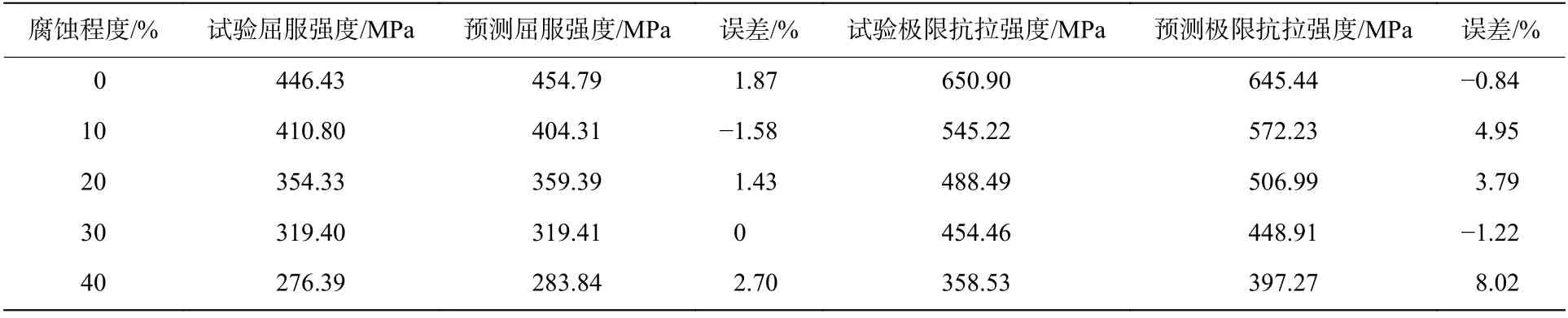
表3 材性参数预测模型计算结果与试验结果对比Table 3 Comparison of calculation results and test results of material parameters prediction model

2.3.2 落锤试验结果分析

钢管试件在落锤作用下在接触位置处首先发生局部凹陷，随着落锤继续下落，中部塑性铰向两端移动，钢管整体产生挠曲，圆钢管出现整体竖向弯曲（W）、局部凹陷变形（δ）和轴向收缩（u）。此过程中，在落锤与钢管的协同作用下，初始动能不断向势能转化，撞击力持续增大而落锤速度不断减小。当落锤速度下降到零时，落锤达到最大撞击深度（λ）（λ 为W 和δ 的耦合），钢管出现弹性恢复行为，并将多余能量“返还”给落锤使其回弹，整个变形过程的示意图如图6 所示。在相同的冲击条件下，腐蚀损伤更加有利于塑性铰的形成和发展。即在落锤侧向撞击下，腐蚀程度高的钢管构件受撞击后更容易发生局部失稳，最终变形对比如图7 所示。

对试件的最终变形、冲击力峰值、作用时间等进行统计，如表4 所示。随着腐蚀程度的增加，冲击力峰值下降，冲击力作用时间增长。当初始冲击能量为1 511.7 J 时，失重率为40%的试件接触力峰值仅为无腐蚀试件的62%，而作用时间延长了143%，并且试件的底部挠曲增大了168%。主要原因是钢管受均匀腐蚀损伤后，构件的变形耗能增加。

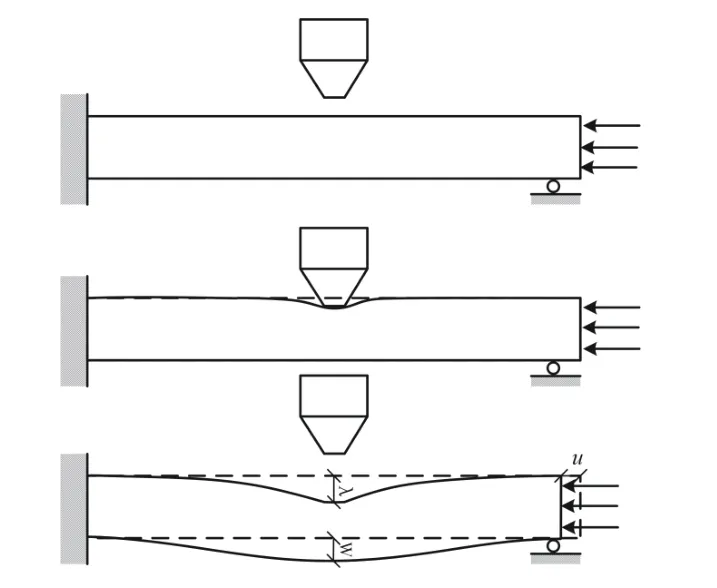
图6 冲击变形过程示意图Fig. 6 Impact deformation process

图7 不同腐蚀程度的冲击变形对比Fig. 7 Comparison of impact deformation of different degrees of corrosion

表4 落锤试验工况Table 4 Drop hammer test conditions

3 刚体撞击Q420 钢管有限元分析

3.1 有限元模型的建立

通过材料参数折减的方法定义大气腐蚀对钢管构件的腐蚀损伤，并采用ABAQUS 软件的显示动力模块进行冲击响应分析。钢管构件采用缩减积分的四节点曲壳S4R 单元，落锤采用四节点三维碰撞刚体R3D4 单元。考虑腐蚀削弱效应，按2.2.1 节所得材料性能参数定义构件本构模型，并考虑应变率效应，选择适用于钢材低速冲击的随动硬化Cowper-Symonds 模型，其表达式为：

通过对刚性锤头施加初始速度的方法实现加载，钢管与锤头的法向接触为硬接触，切向库伦摩擦系数取0.3。为节约计算时间并保证精度，对钢管构件采用五区段分段加密的形式进行网格划分，网格划分完成后共计1 000 个钢管单元体，5 561 个锤头单元，相应模型如图8 所示。

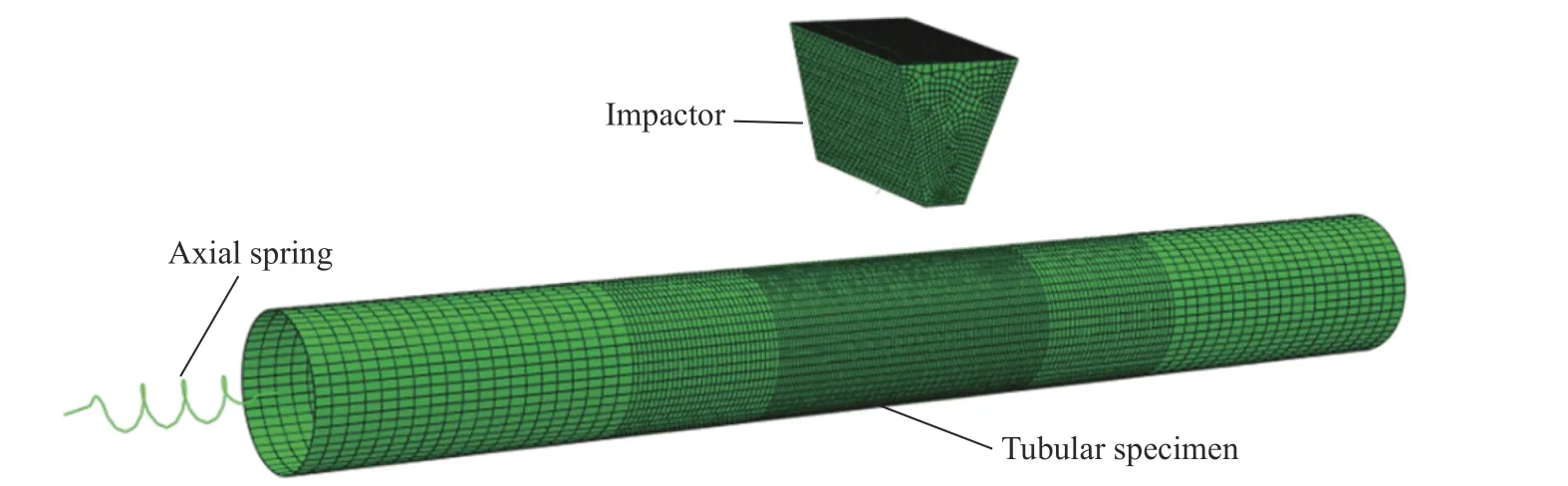
图8 仿真模型及网格划分Fig. 8 Simulation model and mesh

3.2 有限元模型的检验

通过对比相同工况下（冲击速度v=5.97 m/s）试验和有限元计算获得的冲击力-时间关系曲线的整体形状和趋势，以验证所建立模型的有效性，如图9 所示。由图9 可知，数值模拟所得结果与试验结果的整体趋势较吻合，随着腐蚀程度的增加，构件与落锤的接触时间增长，相应的冲击力峰值减小。

由于受到试验中的人工误差、本构模型预测时的计算误差、试验落锤不为理想刚体以及钢管应变速率差异等因素的影响，数值模拟结果与试验结果之间存在偏差。计算值的局部峰值点略高于试验值，而响应时间比试验值略短，但曲线趋势和碰撞中的整体冲量（即力时程曲线所包含的面积）基本吻合，表明该数值模型是合理有效的。

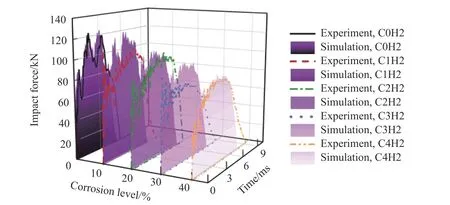
图9 v=5.97 m/s 时冲击力响应计算结果与试验结果对比Fig. 9 Comparison of impact force calculation results and test results at v=5.97 m/s

3.3 撞击参数对响应结果的影响分析

3.3.1 腐蚀程度的影响

考虑腐蚀削弱效应，按3.1 节中的建模方式建立有限元模型，选取落锤质量为54.70 kg、初始速度为7.43 m/s，并根据2.2.1 节获得的材料模型设置7 种腐蚀程度下（0%、10%、20%、30%、40%、50%、60%）的本构参数，对比分析不同腐蚀程度的Q420 钢管的响应情况，分别如图10 和图11 所示。

图10 相同冲击条件下不同腐蚀程度的钢管模型变形Fig. 10 Deformation of steel tube model with various degrees of corrosion under the same impact conditions

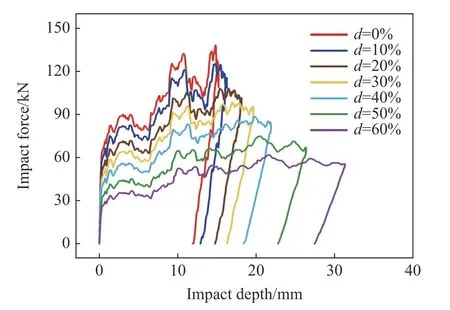
图11 不同腐蚀程度的冲击力-撞深关系曲线Fig. 11 Impact force-depth relation curves with different corrosion degrees

相同冲击作用下，大气腐蚀损伤有利于试件受撞时塑性铰的形成与发展，随着腐蚀程度增加，钢管塑性区域扩大，最终凹陷变形增加并逐渐出现明显的挠曲和轴向收缩。同时，本文中将腐蚀损伤定义为钢材名义屈服应力的折减，钢管屈服应力σy随着d 的增加而减小，由于撞击力大小与σy成正比[3]，相应的冲击力峰值也减小。因而随着腐蚀程度增加，冲击力峰值减小，而落锤撞击深度则不断增加。

图11 所示的数值计算结果与实际趋势相符，即大气腐蚀损伤降低钢管构件对外部冲击的抗力，并促进试件产生塑性变形，不利于整体结构稳定。通过冲击力-撞深关系曲线计算得到各腐蚀程度下钢管的抗冲击刚度退化和撞击过程中构件变形吸收能量情况，如图12 和图13 所示。由图12 和图13可知，大气腐蚀损伤会提高构件的柔度，在承受相同的冲击能量时，腐蚀程度高的钢管对撞击体的抗力不足，将吸收更多动能并以整体变形的形式耗散。

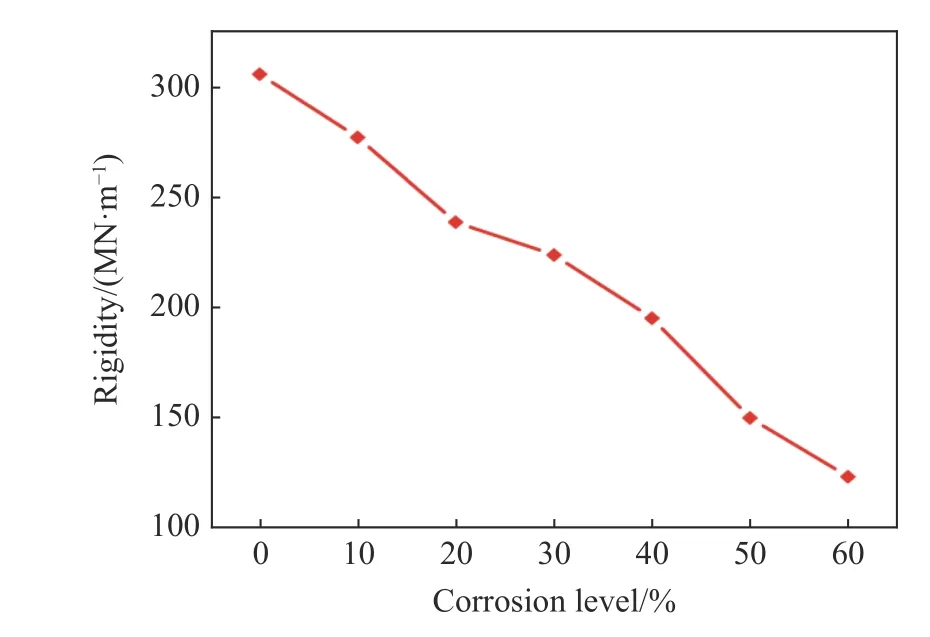
图12 钢管构件的刚度退化情况Fig. 12 Stiffness degradation of steel tube components

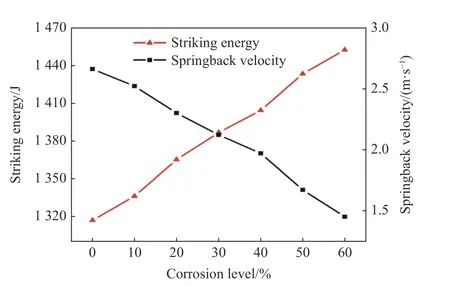
图13 不同腐蚀损伤程度下的冲击能耗趋势Fig. 13 Trend of impact energy consumption under different corrosion damages

3.3.2 落锤速度的影响

由于落石、车辆等撞击体的速度存在较大差异。通过改变落锤速度的方法研究构件在不同冲击速度下的响应规律及大气腐蚀的影响。所得同一腐蚀程度下的撞击深度-时间曲线如图14 所示，不同腐蚀程度和初始速度下的冲击力时程曲线如图15 所示。

钢管本身对外部撞击存在抗性，受冲击时通过对锤头回弹做功和自身变形的形式耗能。随着冲击速度的增大，钢管构件所吸收的能量不断增加，导致冲击力峰值和撞击深度不断增大。当吸收的能量超过构件承受的极限时，钢管主要耗能方式是通过自身变形将动能转化成变形能，因而冲击力峰值增加不明显而撞击深度仍增加，在冲击力时程曲线（图15）上会出现明显的平台段。大气腐蚀会导致钢管构件的抗冲击性能下降，如未腐蚀钢管构件在受到冲击速度为9.72 m/s 的物体撞击时才开始出现平台段，而腐蚀程度为40%的钢管构件在承受速度为7.43 m/s 的物体撞击时已经开始出现平台区域。

图14 腐蚀程度d=0%下的撞击深度-时间曲线Fig. 14 Impact depth-time curves at d=0%

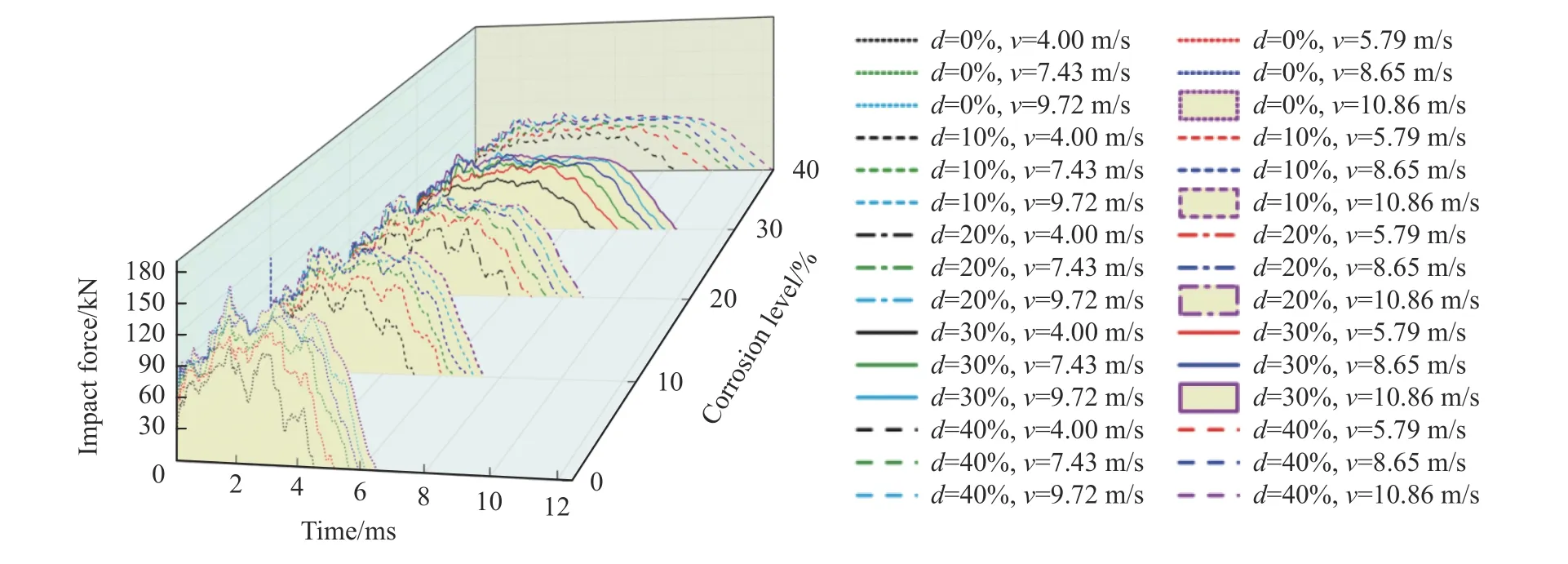
图15 不同腐蚀程度和初始速度下的冲击力时程曲线Fig. 15 Time-history curves of impact forces at different corrosion degrees and initial velocities

3.3.3 落锤质量的影响

改变落锤质量同样会造成初始动能的变化，通过改变落锤质量对比不同质量体撞击钢管构件的响应情况，分析撞击体质量与速度对冲击响应的影响，结果如图16 所示。由图16 可知，随着初始动能增加，响应的撞击力峰值和作用时间都会增加，但冲击物的质量与速度对钢管冲击动力响应的影响不同。当撞击体速度恒定时，质量的改变对作用时间影响较大；而在恒定质量条件下，冲击速度的改变对撞击力峰值影响更明显。如初速度为7.43 m/s 的冲击体，其质量从38.10 kg 增加到71.22 kg 时所获得的初始动能增量，与质量为54.70 kg 的物体，冲击速度从4.00 m/s增大到7.43 m/s 时增加的动能相当，前者作用时间增幅更大，但冲击力峰值增量更小。

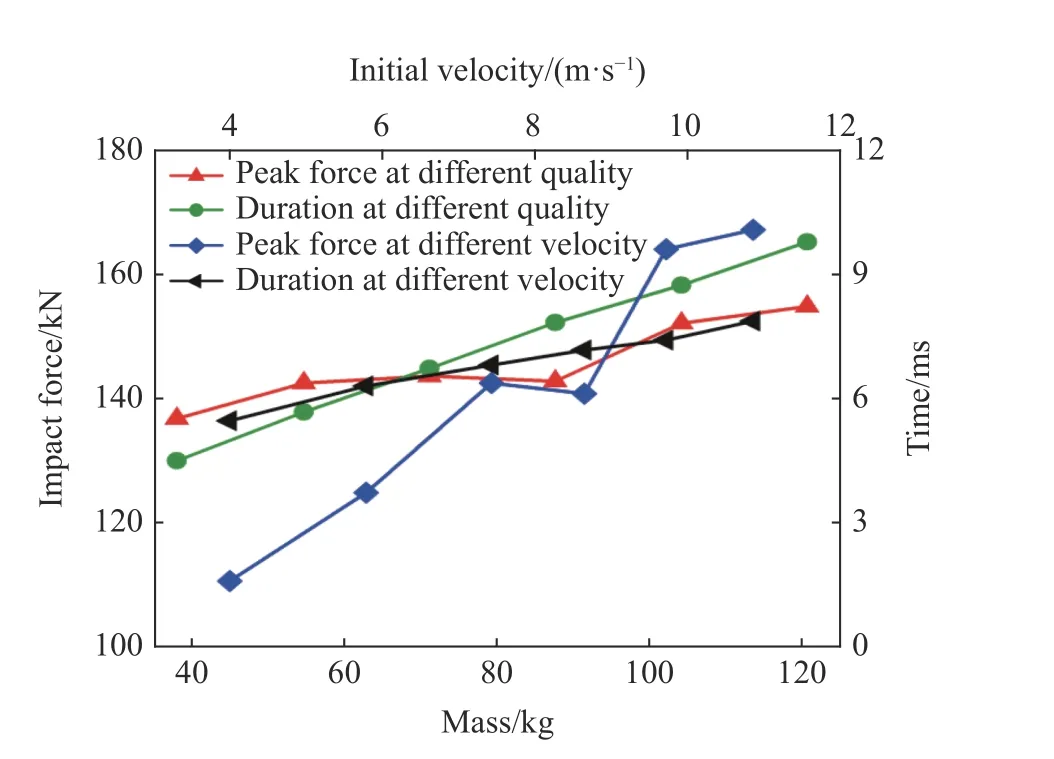
图16 不同冲击条件下的响应规律对比Fig. 16 Comparison of response laws under different impact conditions

4 结 论

大气腐蚀对钢管构件的抗冲击性能有较大影响。本文基于Voce 本构关系提出了低合金钢材的大气腐蚀损伤退化模型，通过开展加速腐蚀试验获得了不同腐蚀程度的Q420 钢材的本构曲线，使用ABAQUS 平台建立了Q420 钢管的预腐蚀损伤模型，分析了不同冲击条件下构件的响应差异。同时，通过Q420 钢管预腐蚀构件的落锤冲击试验验证了有限元模型的正确性，综合试验和计算结果，获得以下主要结论：

（1）大气腐蚀损伤导致Q420 钢材的力学性能参数发生明显改变，材料的名义屈服强度和名义极限抗拉强度随着腐蚀程度的增加而降低，使得钢管构件在撞击过程中产生的冲击力峰值减小。

（2）大气腐蚀降低了Q420 钢管的抗弯刚度，致使其抗冲击极限下降。当构件的腐蚀程度增加时，其受撞后的最终变形增大，更多的冲击能因转化为变形能而耗散，即长期的大气腐蚀损伤不利于结构的抗侧向撞击稳定。

（3）对于相同腐蚀程度的Q420 钢管，撞击体的质量和速度对其冲击响应的影响略有差异，在动能增量相同的情况下，惯性大的物体更容易与构件长时间接触，而初始速率对碰撞过程中撞击力峰值的影响更明显。