基于改进鲸鱼优化算法的多目标信号配时优化
吴小龙,胡 松,成 卫
(1.昆明阡陌交通工程咨询有限公司,云南昆明650028;2.昆明理工大学交通工程学院,云南 昆明650500)
0 引言
我国经济的高速发展大大刺激了国民的物质需求,私家车出行因为其灵活性和方便性也因此被越来越多的人选择.由于城市化的推进和私家车保有量的快速提高,城市交通问题已成为影响城市经济发展的一个重要因素.我国的早期交通规划化与和现有的通行能力需求并不成正比,城市路网负荷超标严重,导致大量城市出现了拥堵的情况.为了在现有的交通条件下尽可能提升交通效益、减少城市的拥堵状况,对交叉口信号控制进行优化是最有效的途径之一.交叉口信号配时优化要考虑多方面的综合因素来进行交叉口信号控制方案设计以达到交叉口的交通效益最优的目的.在评价交叉口通行效益时通常用停车延误、停车率、车辆排放、通行能力等指标来进行.国内外学者在交叉口配时优化上做出了很多研究:Webster配时法是以交叉口车辆延误的估计为基础,通过对周期长度的优化计算,确定相应的一系列配时参数的经典配时算法[1];国内外还开发了许多有关信号控制的软件系统如Synchro等[2];文献[3]针对交通流的时变特性,建立了以延误、排队长度和停车次数最小为目标的交叉口多目标信号配时优化模型,并结合实例证明了模型的有效性;文献[4]使用解析法来构建函数模型,并引入了基于排队论的理论模型,结合人工操作经验来完成交叉口的信号控制,但是该方式在情况复杂和波动性较大的城市交通中适用性不高.近年来,各种启发式算法的兴起使得交叉口配时的方法有了新的发展方向,已经有大量将启发式算法应用于交叉口配时优化的研究:文献[5]构建了车辆和行人总延误最小的信号配时模型,使用遗传算法寻优获得交通实体产生的平均交通延误达到最小的方案;文献[6]改善了过饱和条件下的信号配时优化模型,以延误最小和通行量最大为目标,使用遗传算法(GA)获得更优的配时方案;文献[7]基于TSTM结合GA算法提出的GATSTM系统能够通过校准系统参数来处理和管理交通网络状况的动态变化;文献[8]通过使用改进的微粒群算法对构建的函数模型求解,获得比传统Webster算法更优的配时方案;文献[9]将模拟退火算法引入自适应控制交叉口中,证明了该方法可以明显提升交叉口的通行能力.
鲸鱼优化算法(WOA)作为一种新兴的元启发式搜索算法,在2016年由澳大利亚的mirjalili等[10]根据观察海洋中座头鲸独特的捕食方式提出,算法通过模拟鲸鱼一系列的捕食行为实现目标函数的求解寻优.WOA算法因其操作简单、参数少而且性能好的特点被大量研究人员所关注并作出了许多相关研究.当前对WOA的研究主要集中在应用和改进两方面.文献[11-12]分别通过引入自适应权重和柯西变异以及随机自适应权重和模拟退火的策略对WOA进行改进,并使用测试函数表明了改进后算法的优越性;文献[13]对WOA进行改进并将其应用到充电站选址的项目上,证明了该算法在工程应用上的有效性.文献
[14]使用WOA进行水资源的配置优化,验证WOA在该领域的适用性.文献[15]则通过对WOA进行电网无功优化调度,实例验证了WOA在解决该问题上的鲁棒性和有效性.
文章提及的遗传算法、模拟退火算法和WOA等在进行求解时都存在着传统启发式算法通有的易陷入局部最优解、收敛精度低等缺陷.本文首先通过使用自适应权重和levy飞行策略对WOA进行改进,提升了WOA的全局寻优能力、局部寻优能力以及收敛精度,并把改进后的算法应用到交叉口信号配时优化中,然后通过构造多目标寻优函数模型并使用ALWOA对其进行寻优求解,获得综合通行效益最高的配时方案.
1 多目标信号配时优化的数学模型描述
进行交叉口配时优化时,优化效果的评价指标主要包括延误时间、停车次数、道路通行能力、饱和度、油耗、尾气排放等.本文选取交叉口的车辆平均延误、平均停车次数以及最大通行能力这三个参数作为优化目标,利用加权的方法将这三个优化目标联合起来构造目标函数并进行寻优,以获取交叉口的最大交通效益.
1.1 交叉口平均延误时间
车辆延误由均匀延误和随机延误组成,本文运用韦伯斯特(Webster)提出的延误时间的计算方法来计算车辆的平均延误时间.由Webster延误计算公式可得相位i的车辆平均延误di如下:

式中:第一部分表示均匀延误,第二部分为随机延误;c表示周期,s;λi是绿信比,表示第i相位有效绿灯时间与信号周期的比值;yij为第i相位第j进口道的流量比;xij为第i相位第j进口道的饱和度;qij为第i相位第j进口道的实际到达的当前交通量,pcu/h.由式(1)可知交叉口的所有车辆的平均延误表示为:

1.2 交叉口平均停车次数
进入交叉口的车辆在信号控制的情况下会产生停车的总次数如式(3)所示:

式中:hi表示第i相位的车辆平均停车次数.由式(3)可得一个信号周期内的交叉口的车辆平均停车次数表示为:

1.3 交叉口通行能力计算
计算交叉口通行能力的方法:首先将交叉口各进口道划分为若干车道组,然后计算各车道组的通行能力,再将各相位的通行能力加起来,最后得到该交叉口一个周期的通行能力,表达式如下:

式中:Qi表示第i相位的通行能力,λi为车道组i的饱和流率.
1.4 目标函数
根据实际到达交通量,通过加权的方式将信号周期内交叉口车辆的平均停车次数、平均延误以及交叉口通行能力联合转化为交叉口信号控制优化目标函数,以控制周期内的有效绿灯时间作为自变量.考虑到路口交通量的变换,对模型在设置权重时要根据实际交通流率进行分配,权重设置为ω1=2∣1-Y∣;ω2=1.5∣1-Y∣;ω3=0.5Y(Y为交叉口各相位关键流率比之和),目标函数如下:

约束条件包括以下几点:

式中:gei为相位i有效绿灯时间,li为相位i损失时间,gimin为相位i的最小绿灯时间,gimax为相位i的最大绿灯时间,cmin为最小信号周期长度,cmax为最大信号周期长度.由目标函数构成可知,要使目标函数取得最小值,就要求在约束条件下尽可能减小车辆的平均延误和停车次数而通行能力则尽量增大.
2 鲸鱼优化算法
鲸鱼优化算法是一种新兴的群智能优化算法,鲸鱼优化算法具有简单、调整参数少、性能高效的特点.算法的主要思路是通过模拟海洋中的座头鲸的觅食行为得到的,把食物位置作为寻优目标通过包围捕食、气泡网攻击及随机游走等方式获得最优解.
2.1 包围捕食策略
鲸鱼个体能识别猎物的位置区域.由于位置的优化设计在搜索空间不是预先确定的,WOA假定当前的最佳解决方案是目标位置或接近目标最优个体位置.在定义了最佳搜索位置之后,个体开始按照一定的策略朝着当前最优位置进行游动.此行为表示如下:


2.2 气泡袭击阶段
描述气泡网攻击行为的数学模型用如下两种方式设计实现:
2)螺旋更新位置:此方法首先计算鲸鱼之间的距离,个体从当前位置朝着最优个体位置进行螺旋式移动,用一个螺旋方程来模拟鲸鱼的螺旋形运动如下:


2.3 搜寻猎物阶段

3 改进的鲸鱼优化算法
为了避免传统的WOA在求解后期容易陷入局部最优导致的算法早熟从而收敛使进度不高的问题,本文改进WOA的思路从以下两个方法入手:一是使用自适应权重方法,使得WOA的局部寻优能力得到提升;另一方法是通过引入levy飞行策略对鲸鱼位置进行更新,以提升WOA的全局寻优能力.
3.1 自适应权重方法
由于WOA的局部搜索实现方式是以公式(10)和公式(13)进行的,当个体以公式(14)的更新方式进行局部搜索时,这种方式只能在局部最优解附近徘徊,而不能实现更好的局部寻优.惯性权重是可以用来平衡算法局部搜索能力和全局搜索能力的重要参数.本文使用了一种呈指数改变的自适应权重方法,算法前期使用较大的权重实现较强的全局搜索性能,保证搜索范围,随着迭代次数的增长,接近最优解时,权重值呈现指数减小,使得算法的局部寻优能力大大提升.自适应权值公式如(17)所示,改进后的位置更新公式如(18)所示:


式中:t表示当前迭代次数,T表示最大迭代次数.
3.2 levy飞行策略
levy飞行这个概念的正式定义是“步长具有重尾概率分布的随机行走”.我们可以说这是一个随机游动,它的特殊性在于它表现出较大的跳跃,因为这个过程的步长来自于一个具有无限方差的分布.与任何随机过程一样,levy飞行起源于扩散过程.正因为如此,它们在随机测量和随机或伪随机自然现象的模拟中很有用,特别是表现出一种反常的扩散,系统中存在一种“微观结构”,与混沌理论有关.levy飞行的过程是实体在进行运动的过程中进行大量的小步长移动,同时还有少量跨越式大步长移动的过程.在Matlab中进行模拟levy飞行的二维平面示意图见图1.

图1 Levy飞行二维平面示意图Fig.1 Two-dimensional diagram of Levy flight
研究发现许多生物的觅食行为符合levy飞行模式,目前也有大量的研究将其应用到一些仿生算法中,并取得了不错的效果.受文献[16-17]启发,本文将levy飞行应用于鲸鱼的位置更新中,在算法进行更新后再进行一次levy飞行更新个体位置,可以实现跳出局部最优解,扩大搜索能力的效果.位置更新的方式为:

式中:α是步长缩放因子,levy(λ)就是随机步长,⊕就是‘·*’运算.2009年,Yang X Y[18-19]把levy分布函数经过简化和傅立叶变换后得到其幂次形式的概率密度函数,使用Mantegna方法[20]生成levy分布随机步长.levy飞行概率密度函数及生成随机步长的公式如下:

即进行更新时,levy(λ)使用S表示;进行计算时,参数β取值为1.5,α取值为1,u~N(0,σ2),v~N(0,1),σ取值为:

3.3 改进WOA的算法流程图
改进WOA通过使用levy飞行策略来跳出局部最优解,避免算法早熟.通过加上自适应权重的方式使得鲸鱼在进行局部寻优时可以提升收敛精度,具体的算法执行步骤如图2所示.

图2 算法流程图Fig.2 Algorithm flowchart
4 算例分析
在进行多目标信号配时优化时,本文选取曲靖市某路口作为实际算例,通过实地调研获得的该路口晚高峰时的路口各个方向的交通量以及现有的配时方案、相位示意图及该路口的平面渠化图,见图3~图4.通过调查获取了该路口的晚高峰小时交通流量(已转化为标准交通量),实际数据如下表1所示.

图3 交叉口相位示意图Fig.3 Phase diagram of intersection

图4 路口平面示意图Fig.4 Junction plan
分别使用ALWOA和WOA对多目标配时优化模型进行寻优求解,模型约束条件设置为配时最小信号周期长为90 s,最大信号周期长为180 s;相位最小有效绿灯时长为20 s,最大有效绿灯时长为60 s;设置算法迭代次数为200,种群个体数为50,变量数为4;通过迭代图可知,GA和基本WOA过早出现了收敛现象,而使用ALWOA则明显避免了算法的早熟现象,而且得到的精度更高,改进前后算法适应度值的收敛曲线分别如图5所示.

表1 实际交通流量统计Tab.2 Actual traffic flow statistics

图5 算法对比迭代图Fig.5 Algorithm comparison iteration diagram
将使用ALWOA进行优化配时得到的方案及优化目标值置于表2中,同时为了验证本文数学模型及算法的有效性,将使用原方案、Webster算法、遗传算法和标准WOA算法得到的结果也置于表2中进行对比.
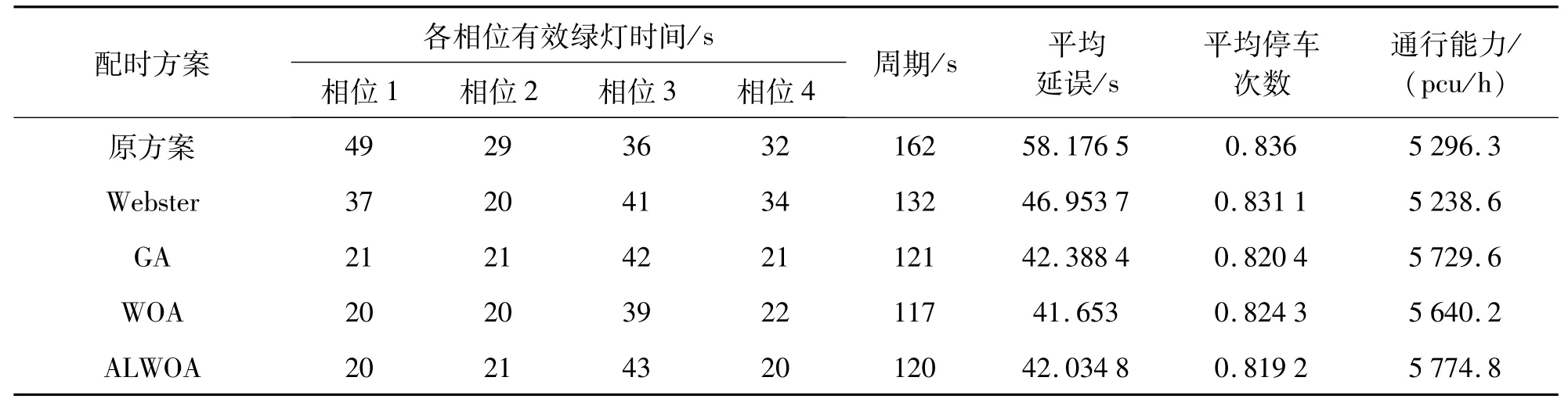
表2 配时方案及优化结果对比表Tab.2 Comparison table of timing scheme and optimization results
由表2可以看出使用ALWOA得到的配时方案与原配时方案及使用Webster法得到的方案相比有了显著的提升,与标准WOA算法和遗传算法相比也有不同程度的提高,结果充分证明了ALWOA在进行交叉口多目标信号配时优化上的有效性.
5 结语
本文通过引入自适应权重及levy飞行的模式对WOA做出了改进,提升了WOA的全局搜索能力和局部寻优能力,使得收敛精度提升.然后将其用在交叉口信号配时优化上,将求解后的结果与基本的WOA寻优得到的结果进行了对比,结果显示使用ALWOA获得的方案优于其余几种优化方法得到的方案,证明了此方法模型的有效性.基于文章只考虑了单点交叉口配时优化的问题,而现实中的城市道路是多个交叉口组成的复杂道路网络,接下来考虑如何使用该模型进行多交叉口协调控制优化方面的研究.

