基于游标细分电感式编码器的误差分析与校正
丁红昌,刘志鹏
(1.长春理工大学,吉林 长春 130012;2.长春理工大学机电工程学院,吉林 长春 130012)
0 引言
角度编码器是一种常见的角位移的检测设备,伴随着人工智能的快速发展,提高智能化、自动化、体积轻量化等检测,是提高检测产品的质量水平和故障诊断重要的有效手段[1-2]。它主要应用在汽车、航空航天[3]、自动化生产线、机器人、军事工程等领域[4-6]。基于电磁互感原理制造出的角位移传感器,是将被测产品机械角度转化成电感线圈(互感)磁通量变化量,最后转变为电信号输出的检测装置,它具有结构简单、体积小、价格比较低廉,且在工作过程中表现出良好的测量精度、高分辨率和极强的抗干扰能力等。与电容式、光电式[7]、机械式[7]、电磁式[8]、磁敏电阻式等相比,电感式传感器[9]有如下优势:①更加轻量化、结构简单、无需维护;②对工作环境要求不高、价格更加低廉;③无接触、无需精安装。
本文主要设计一种基于游标细分原理的时栅码盘新型编码器,该传感器由定子和转子构成,其中把转子定子内部做成栅型。栅型码盘由两条码道组成,主码道(Master)由256对栅极组成,游标码道(Nonius)由255对栅极组成。其简单结构如图1。时栅利用这种类似“粗机+精机”的结构形式,可使角度传感器获取精准的绝对位置信息。

图1 两码道游标码盘极板
1 绝对式游标码盘在编码器中的应用
1.1 游标式编码器原理分析
在工程领域内,几乎都会接触到一种简单测量工具——游标卡尺(图2)。游标卡尺在测量被测物体时,其读数由主尺部分和游标尺部分组成。为了可提高游标卡尺测量精度,游标尺上的10个分度栅格与主尺上的9个分度格设置相等的长度。所以每个主尺分度栅格与游标分度格栅的距离只差为0.1mm。基于这种游标错位放大原理,一个50分度的游标卡尺就可以实现测量精度为0.02mm的测量。
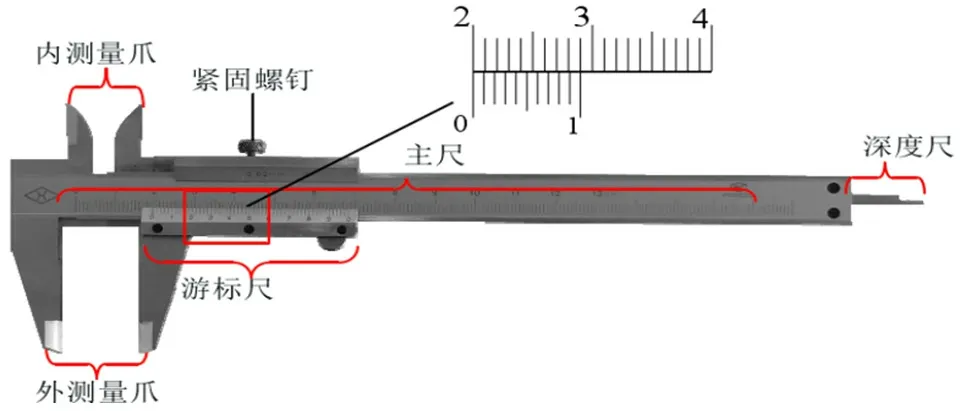
图2 游标式卡尺示意图
根据这种游标原理,编码器目前有两种游标码盘,第一种是“精机+粗机”绝对式时栅测量方案,其中码盘上m对极传感器相当于游标主尺,m-1对极传感器相当于游标卡尺。另一种码盘有三个码道:外圈有m对极,中圈有m-1对极,内圈有m-n对极,目前大部分厂家使用第一种码道编码方式以便于获得体积较小、分辨率较高、更有利于刻画的编码器。这两种游标码道并不能像游标卡尺可以在随意滑动,而是有相应位置的刻画在码盘上。假设从零点开始,第m格的游标刻线与主码道的第n条刻线的角度差为µ:

1.2 游标式码盘的应用
对于游标码盘上的码道,在同刻上的n刻线和m刻线的位置是唯一的,即主码道上的磁对数相对于游标码道上的磁对数的位置也是惟一的,当编码器在进行整周的测量中时,当转子转动范围在一个机器周期内时,n-1对极和n对极的传感器测头所感应的信号周期分别经过了N-1和N次变化,当完成整个周期测量时,传感器的粗码道和精码道对应输出电压信号正好相差一个周期,即可在任意时提取出任意一个一对极的变化情况,在一个极对变化空间内,由粗机和精机分别对应的输出信号所确定的相位之差可以唯一表达出角度精度位置,类似于两点确定一条直线,即而实现绝对测量,如图3所示。
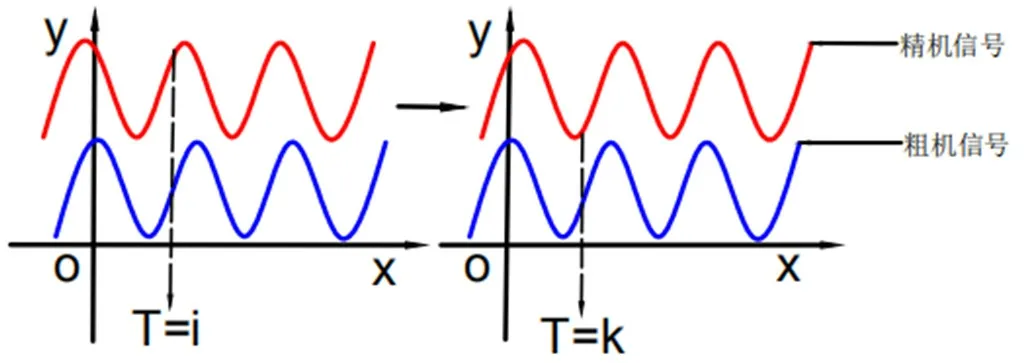
图3 粗机+精机信号示意图
2 游标式码盘误差及范围求解
2.1 码盘误差
本文主要研究在其它误差都精确的前提下只考虑码盘刻画误差。可知,粗码道主要测量角度的整数位,对其编码器的影响比较大,精机主要测量角度的小数位。因此本文只考虑粗码道的码盘刻画误差对编码器的影响,精码道的刻画误差在本文即为准确值。由电气角度=机械角度×极对数,可得粗机刚好转过一个极对数,在没有误差的情况下粗机信号正好转过一个周期,而实际码盘有误差的存在,会相对于理论信号有一定的偏差,码盘误差示意图如图4所示。
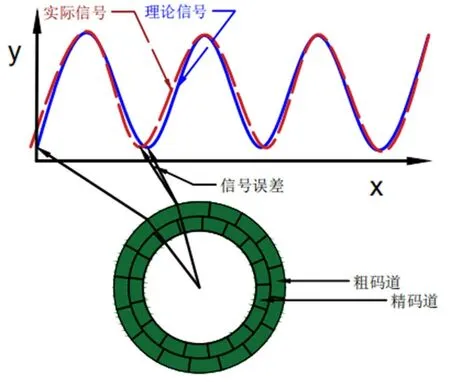
图4 码盘误差示意图
2.2 码盘误差范围求解
正余弦函数信号是以2π为周期的函数,因此机械角度不能用电气角度除以极对数求得,所以有:

变换可得:

则有:

实际的机械角度为:

Χ信号是粗机角度信号补偿后的信号,Y信号是精机角度补偿后的信号。由游标原理和计算可知,存在如下两种情况,误差信号为γ为正偏时和误差信号γ为正偏时,如图5所示。
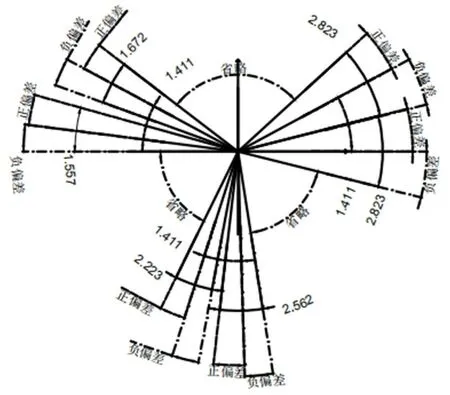
图5 角度偏差示意图
机械转角φ在[],偏差以0°为中心的正负偏差;机械转角φ在[],偏差以为正负偏差。因该粗机有255个极对数即有255个偏差范围,直到[]。以[]范围为例,与[]范围内的偏差范围不能有交集,否则不能保证偏差范围的唯一性。可知外边界为[],让其内边界相等,则有:

根据上述分析可得,机械角转过一个极对数对应的角度,正余弦信号变化一个周期所对应的的最大误差为:±0.7031°,因此误差越小,产生跳码的几率就越小,编码器就越准确。
3 码盘误差分析
3.1 误差求解
由上文知:

两式作差为:

可令:

则有:
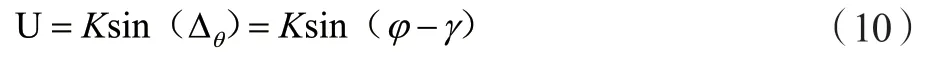
角位移传感器的输入输出特性,即传感器的模型表示为:

其中:Χ为被测机械角度位移量;U为编码器在极对数处的电压值。在数据测量部分非线性环节有Y=g(u),期望整个检测系统的输入输出呈现理想形,即Y=Χ=ƒ(U)。
由上式可知,该环节与编码器模型成反函数的输出特性,则可以实现对编码器输出实际值的求解。对上式泰勒展开表达式为:
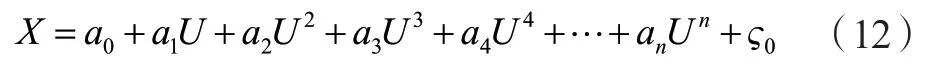
其中:a0~an为常数;为高阶无穷小。
根据编码器精度要求,则选择n=3,则上式可改为:

从上式可知,确定该环节主要为求出系数a0~an的解值。由上式可得到实际Χ值与理论值之间必存在误差其方差为:

均方差表示为:
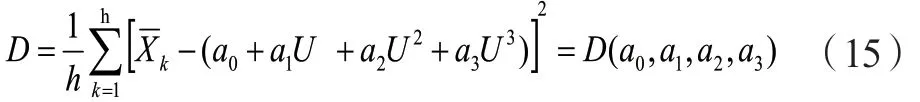
由上式得,均方差D是系数a0~a3的函数,由于多元函数条件极值,可将函数D(a0,a1,a2,a3)分别对系数求偏导,即令各个偏导数等于0,有:
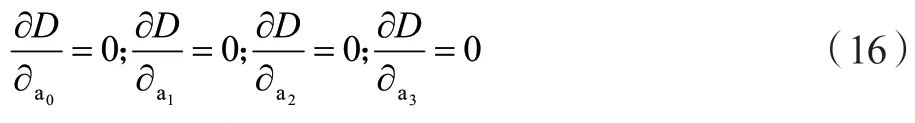
从上式可得知:
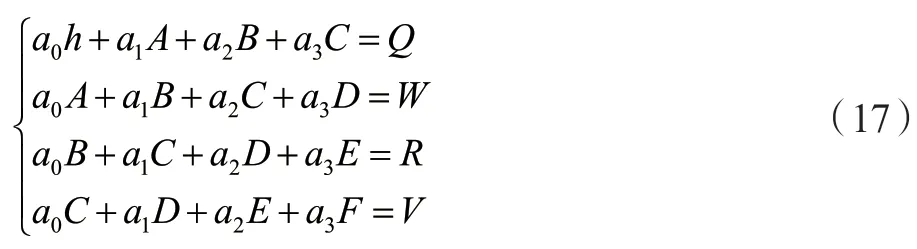
式中:h为理论值个数;为编码器电压输出值Uk之和;为理论值之和;。
3.2 参数的求解
把2 5 5对磁对数对应的角度Δθ代入式U=Ks i n中可求出对应的电压值Uk(令k=5,并以16对为例),如表1所示。 把表1数据代入式(1)中可求各数值得:h=16,A=5.5184,B=4.2785,C=3.7301,D=3.4418,E=3.3146,F=3.3182,Q=63.9254,W=49.2984,R=42.8677,V=39.6973。将上式各值代入(2)中求得:a0=2.7939,a1=3.7969,a2=21.2455,a3=-8.4613。继而求得角位移传感器的实际值表达式为:
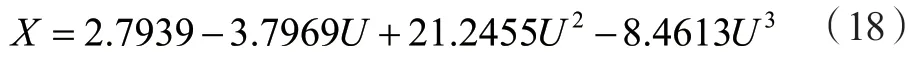

表1 电压数值
3.3 误差结果
将表1的标定点代入上式中,得到实际的系统输出电压值,如表2所示。
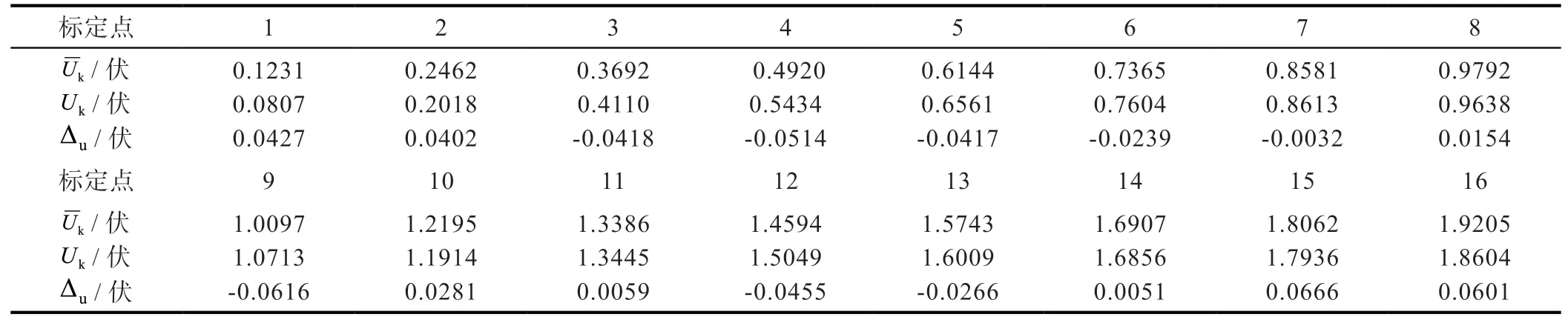
表2 系统输出电压值
传感器经过上述特性曲线可得,最大极差为:0.0666,系统标准方差为0.04147,由上文可知编码器转过一个极对数最大偏差为:1.4062,即有转过每个极对数的相对误差为:
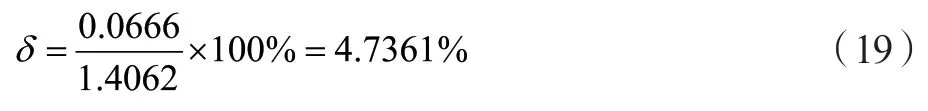
4 校正仿真实验
由MATLAB仿真,可知曲线1为理论曲线为在角度传感器在无误差情况下时转过每个极对数对应的值,曲线2为转过每个极对数的实际曲线,曲线3为角度传感器相对应转过各个极对数时,实际曲线与理论曲线的差值,即为误差曲线。每转过一个极对数,实际曲线与理论曲线在极对数处的差值是不同的,即误差曲线呈不规则的特性线条,如图6所示。
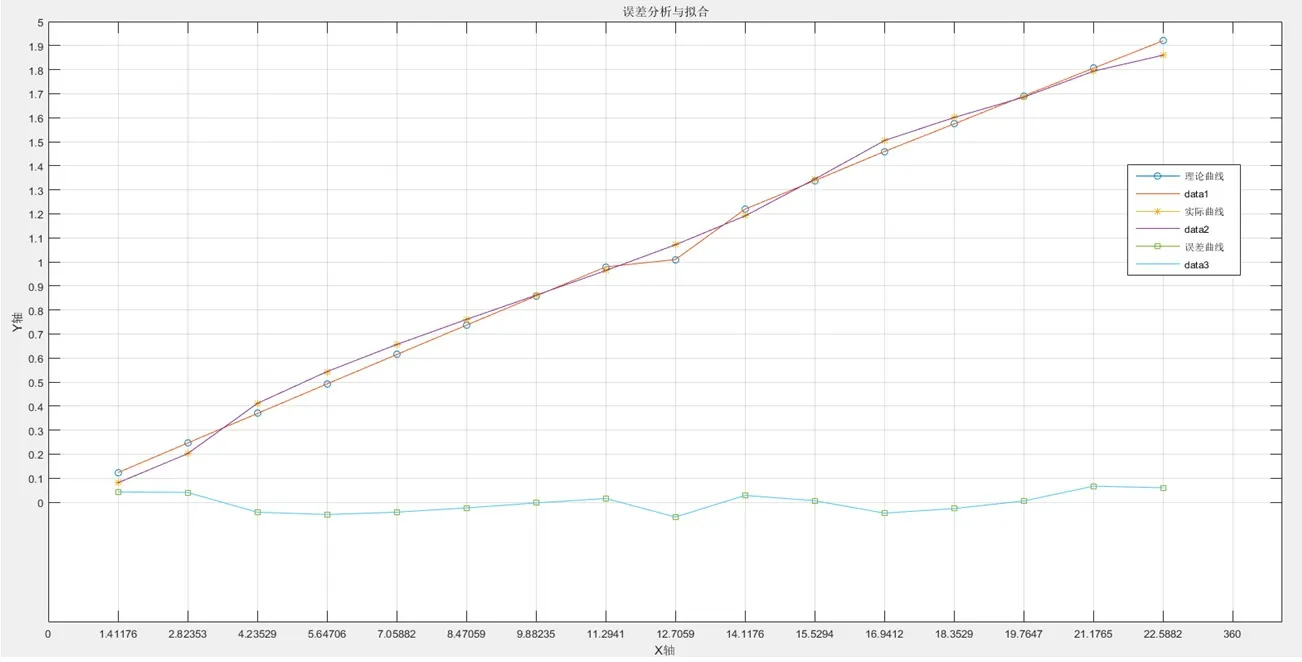
图6 仿真实验图
对误差曲线进行拟合使其找到一条与误差曲线拟合效果较好的一条特性曲线MATLAB仿真可大致找到一条误差拟合曲线4,拟合效果如图7所示。
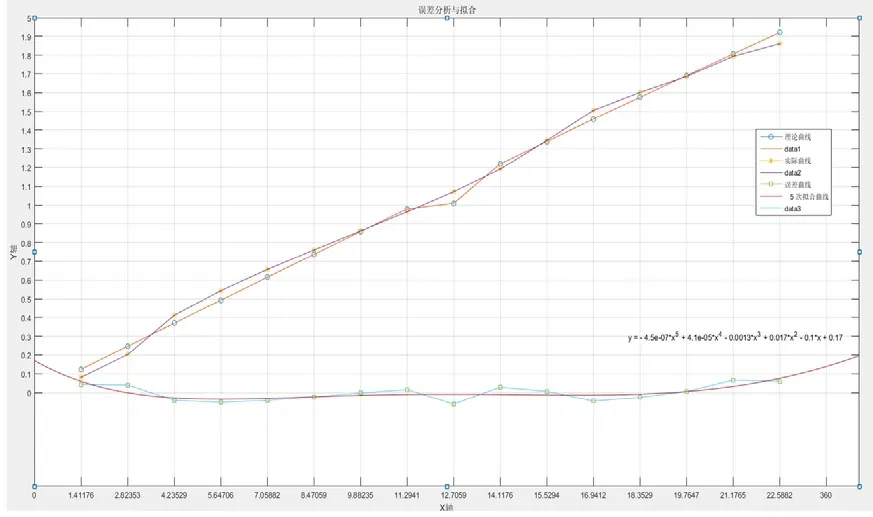
图7 仿真实验图
由仿真可得实际曲线与误差拟合曲线公式组合,所得到的误差曲线很大程度上逼近理论曲线,即编码器转过各个极对数的误差可减小到相对于校正前的实际值与理论值的误差的一个数量级。对比校正前后采用特性曲线补偿后,转子转过各个极对数最大偏差为0.00614。
相对误差为:

5 校正结果分析
对比采用特性曲线补偿后,转子转过各个极对数最大偏差为0.00514,相对误差为:

可知校正前最大偏差为0.0666,相对误差为:
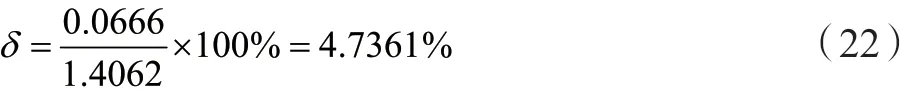
由分析可知,校正前与校正后相比,误差减小了一个数量级左右。校正后编码器每转过一个粗机极对数对应的电气角度的实际值与理论值的误差值很大程度上得到改善。
6 结语
本文对游标细分电感式编码器的误差进行了分析与校正,在误差方面进行了传感器转子每转过一个极对数产生的误差且求得公式,并与传感器的理论值进行分析,利用MATLAB仿真求得误差特性曲线。在校正方面,利用仿真找到对误差曲线拟合效果较好的曲线,并求得拟合曲线方程。最后使其实际曲线与误差拟合曲线进行组合,实践证明,在很大程度上减小了校正前误差,使该编码器错码率大大降低。

