基于贝叶斯网络的油田管道失效概率计算

任伟建, 于 雪, 霍凤财, 康朝海

(东北石油大学 a. 电气信息工程学院； b. 黑龙江省网络化与智能控制重点实验室, 黑龙江 大庆 163318)

0 引 言

油田管道在运输过程中易受到腐蚀、 管道设计缺陷、 误操作、 第三方破坏等因素的影响, 从而引起管道发生泄漏, 造成重大的环境污染和巨大的经济损失。如何科学地对油田管道进行失效风险分析对管道的安全运行具有重要意义。

目前国内外管道失效风险评估方法主要有灰色关联分析法[1]、 层次分析法[2]、 多属性决策理论[3]、 事故树分析法[4]和贝叶斯网络法[5-7]。其中, 事故树分析法因其具有强大的致因分析能力而被广泛使用, 李震等[8]利用事故树分析法构建了海洋平台风险模型并求出该模型顶上事件发生的概率； 王鹏飞等[9]对罐车爆炸事故树中基本事件的结构重要性系数进行了计算并排序, 确定了事故发生的主要因素； 马超等[10]采用事故树分析法计算化工事故的危害度及节点重要度实现了事故的预警； 陈星星等[11]针对船舶泄漏事故建立了事故树模型, 通过模型底事件概率算出顶上事件发生概率, 但无法通过顶上事件概率推理出底事件概率； 刘小燕等[12]引入事故树分析法探究施工人员高空坠落事故的发生原因并找到事故发生的潜在原因。事故树分析法受限于静态属性, 不能对事件进行二态性分析, 且无法实现逆向推理, 当事件因素不断发生变化时, 其事故概率无法随之变化, 因此单一采用事故树分析法评估事件风险仍存在一定的局限性。

贝叶斯网络是一种不确定性的因果推理模型, 主要用于概率推理和决策, 许多学者利用贝叶斯网络构建管道贝叶斯网络模型实现管道失效概率的计算。Li等[13]利用贝叶斯网络动态地计算了海底管道失效概率； 魏亚荣等[14]通过建立页岩气集输管道贝叶斯网络模型计算了管道失效概率并确定了影响管道失效的关键因素； 王春雪[15]利用贝叶斯网络理论建立了城市燃气管道泄漏风险模型实现了管道风险预测。贝叶斯网络中的参数通常由专家知识经验确定, 使参数具有较强的主观性和不确定性, 并且在实际风险中, 风险是随机产生的, 其发生变化时相应的参数也会改变, 最终无法保证推理结果的准确性和实时性。现有的贝叶斯网络参数学习方法大多采用期望最大化算法, 但该算法在数据缺失情况下效率并不高, 计算量随缺失数据集大小呈线性增加, 导致参数依然存在严重的误差问题。为了解决这个问题, 笔者引入遗传算法进行参数学习, 旨在保证算法收敛速度的同时提升参数的精度。

笔者针对事故树具有静态属性且无法实现逆推理的缺陷, 提出一种基于贝叶斯网络的管道失效概率计算方法。首先, 利用事故树建立管道失效事故树模型, 通过事故树与贝叶斯网络的转化确定管道失效贝叶斯网络模型的结构； 其次, 考虑到由专家知识经验及期望最大化算法获取网络参数存在较大的估计误差问题, 引入遗传算法改进贝叶斯网络参数学习以此获取网络最优参数； 最后, 针对实际数据采用笔者方法计算管道失效概率并与传统贝叶斯网络法进行比较与误差分析, 验证改进后贝叶斯网络模型的有效性。

1 贝叶斯网络

贝叶斯网络是基于图论和概率论的有向无环图, 用于表示随机变量间的概率分布与依赖关系, 由节点、 有向边和概率组成。贝叶斯网络包括网络结构和网络参数两部分, 网络结构对应一个有向无环图, 用于表示问题域中变量之间的因果关系, 网络参数对应网络中每个节点相对父节点集的条件概率分布表(CPT： Conditional Probability Table)。设一个系统U的贝叶斯网络G={N,υ}, 其中N表示为贝叶斯网络的结构,υ表示网络参数, 其贝叶斯网络模型如图1所示。

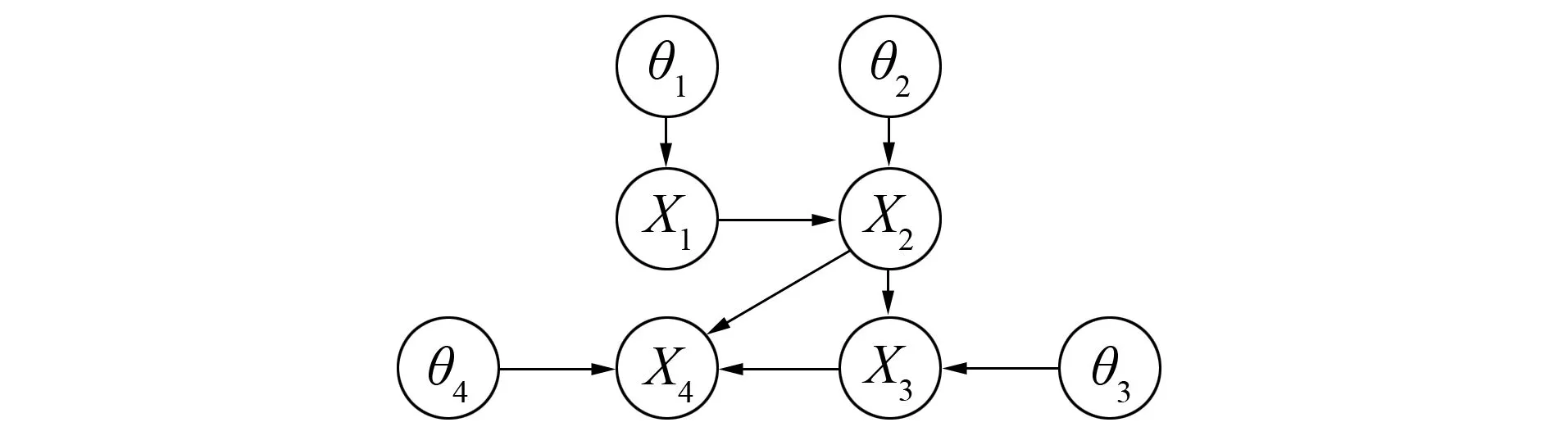
图1 贝叶斯网络示意图Fig.1 Bayesian network diagram

图1中X1、X2、X3、X4代表一组随机变量, 箭头表示随机变量的依赖关系,X1指向X2,X2指向X3、X4,X3指向X4,X1是X2的父节点,X2为X3的父节点,X4为X2和X3的子节点, 父节点又叫做根节点, 根节点代表先验概率的分布, 非根节点对应条件概率分布(CPD: Conditional Probability Distribution)。设X=(X1,X2,…,Xn)为事件的变量集合, 贝叶斯公式表示为

(1)

其中P(Xi)和P(Xj)为先验概率,P(Xi|Xj)为条件概率,P(Xj|Xi)为后验概率。在贝叶斯网络参数学习中其模型参数是不确定值, 它能随机发生变化且满足一定分布。贝叶斯参数学习是根据已知的数据集D估计参数的概率分布, 再用得到的参数概率分布计算随机变量X的后验概率分布。图1中贝叶斯网络只包含{X1,X2,X3,X4}4个节点, 集合υ={θ1,θ2,θ3,θ4}中的元素是每个节点对应的参数, 且每个参数θi表示一组条件概率分布(CPD), 即θi=P(Xi|Pg(Xi)),Pg(Xi)表示为Xi的父节点, 可理解为网络中任一节点在其父节点某一状态条件下事件Xi发生的可能性大小, 由于任意θi和θj(i≠j)之间没有直接相连的边, 因此每个θ之间是独立的。所以有

(2)

如果观测到一个样本X, 即{X1,X2,X3,X4}都已知, 则ϑ={θ1,θ2,θ3,θ4}4个元素中任意两个量之间是彼此独立的。若样本X已知, 则观测到的一个数据集D这一性质依然成立, 因此υ在观测到数据集D后的后验概率可以写成

(3)

通过网络中根节点的先验概率和每个参数的CPT, 利用联合概率分布可以直接计算系统U发生的概率

(4)

其中Xi为网络中的子节点；n为网络节点数量。

2 油田管道失效风险贝叶斯网络模型

2.1 管道失效风险贝叶斯网络结构的确定

利用贝叶斯网络计算管道失效概率, 首先必须解决网络结构的构建问题。观测部分数据实现贝叶斯网络结构自主构建具有难度大、 耗时长且无法保证网络结构的完整性问题。为此, 笔者首先利用事故树分析法建立管道失效事故树模型, 然后利用事故树与贝叶斯网络的转化确定网络结构, 完成管道失效风险贝叶斯网络模型结构的构建。

2.1.1 管道失效风险事故树模型

事故树也叫做故障树, 该方法将最不希望的是系统事故状态作为逻辑分析的顶上事件, 通过找出导致顶上事件状态可能发生的所有直接原因, 此事件称为中间事件, 继而再跟踪找出导致这些中间事件可能发生的所有直接原因, 直到找出引发中间事件发生的全部事件, 这些事件称为底事件。每个事件通过相应的逻辑符号及逻辑门将底事件、 中间事件、 顶上事件连接成树形逻辑关系图, 此特殊的倒立树状逻辑关系图用逻辑门符号、 转移符号和事件符号描述系统中各种事件之间的因果关系。通过对管道风险因素进行详细地辨识, 将管道失效风险作为顶上事件, 自上而下以此分析导致该影响因素发生的中间事件以及基本事件, 每个风险事件的符号与名称如表1所示。

表1 管道风险分析

通过对管道风险因素深入研究, 将风险因素划分为4类, 即腐蚀、 制管缺陷、 操作失误和第三方破坏。以管道失效E作为顶事件, 中间事件分别以M1、M2、M3、M4表示腐蚀、 制管缺陷、 操作失误和第三方破坏, 其中, 腐蚀可以分为两类, 即管道内腐蚀和埋地腐蚀, 用符号依次表示为X1、X2； 制管缺陷因素主要有管道设计标准缺陷、 防腐设计缺陷、 防灾害设计缺陷, 符号依次表示为X3、X4、X5； 人为主观因素操作失误也叫做误操作, 其中包括施工操作失误、 管道运行和维护失误, 依次表示为X6、X7、X8； 在第三方破坏风险因素中人为破坏和地质灾害符号依次表示为X9、X10。所建立的管道失效风险事故树模型如图2所示。

图2 管道失效事故树模型Fig.2 Fault tree model of pipeline failure

2.1.2 事故树的贝叶斯网络化

由于事故树分析法受限于静态属性, 不能对事件进行二态性分析, 且无法实现逆向推理。当事件因素不断发生变化时, 其事故概率无法随之更新, 采用事故树分析法计算管道风险顶事件概率仍存在一定的局限性。而贝叶斯网络在处理动态事件具有一定的优势, 事故树与贝叶斯网络相比其优点如下。

1) 贝叶斯网络对事件能进行多态性分析。而事故树对所有事件的描述仅有正常和失效两种状态, 针对事件存在的多状态事件, 采用事故树分析法难以描述。

2) 贝叶斯网络适用概率描述管道风险的逻辑关系更具有一般性。事故树中对门的描述是确定的逻辑关系, 需要上下级事件具有确定的因果关系, 但对复杂系统而言, 其上下级事件之间可能存在不确定的因果关系。

3) 贝叶斯网络利用联合概率分布直接求任意节点的失效概率。事故树法计算顶上事件和中间事件的发生概率则具有很高的复杂性, 它需要先求出系统所有的最小割集, 再利用容斥定理进一步计算。

4) 贝叶斯网络利用自身推理算法很容易就可以求得底事件的重要度。事故树对复杂系统的重要度计算相对繁琐。

从系统状况的描述可看出, 事故树中的事件与贝叶斯网络中的节点是完全对应的, 同时在推理机制方面存在极大的相似性, 这就决定了事故树与贝叶斯网络可以进行转化。因此, 笔者提出事故树构建贝叶斯网络模型的步骤如下：

步骤1 针对事故树的基本事件、 中间事件和顶上事件, 在贝叶斯网络中建立父节点、 中间节点和子节点, 若事故树中存在多个相同的基本事件, 则在贝叶斯网络中只需设定一个节点, 并对贝叶斯网络每个节点名称进行命名；

步骤2 事故树之间的逻辑关系与贝叶斯网络的有向边相互映射；

步骤3 事故树基本事件的失效概率映射为贝叶斯网络中父节点的先验概率；

步骤4 事故树的逻辑门映射为贝叶斯网络中各节点的条件概率。

基于以上步骤, 可将事故树转化为贝叶斯网络模型, 其转化示意图如图3所示。

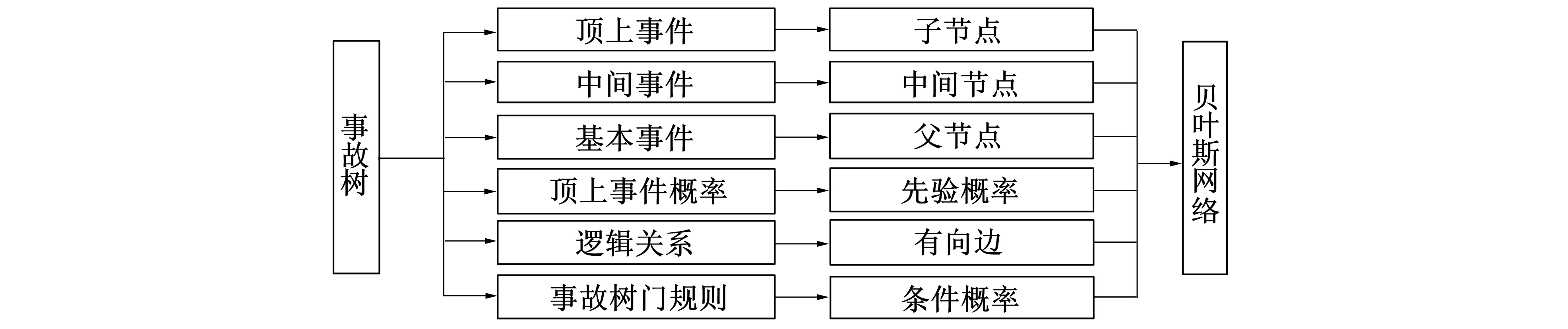
图3 事故树的贝叶斯网络化Fig.3 Diagram of fault tree transformation to Bayesian network

2.1.3 管道失效风险贝叶斯网络结构的构建

利用事故树的贝叶斯网络化建立管道失效贝叶斯网络模型, 首先将事故树的顶事件E转化为贝叶斯网络子节点T, 中间事件M1、M2、M3、M4转化为贝叶斯网络中的中间节点A、B、C、D, 基本事件{X1,X2,…,X10}转化为网络中的根节点； 然后将事故树中的因果逻辑关系转化为网络中随机变量的依赖关系, 且A、B、C、D均指向T, 根节点{X1,X2,…,X10}分别指向他们的子节点； 最后将管道事故树模型基本事件概率映射为贝叶斯网络根节点的先验概率, 同时相应的“或”门映射为贝叶斯网络中条件概率。图4网络节点符号对应风险因素如表2所示。

图4 管道失效风险贝叶斯网络模型Fig.4 Bayesian network model of pipeline failure risk

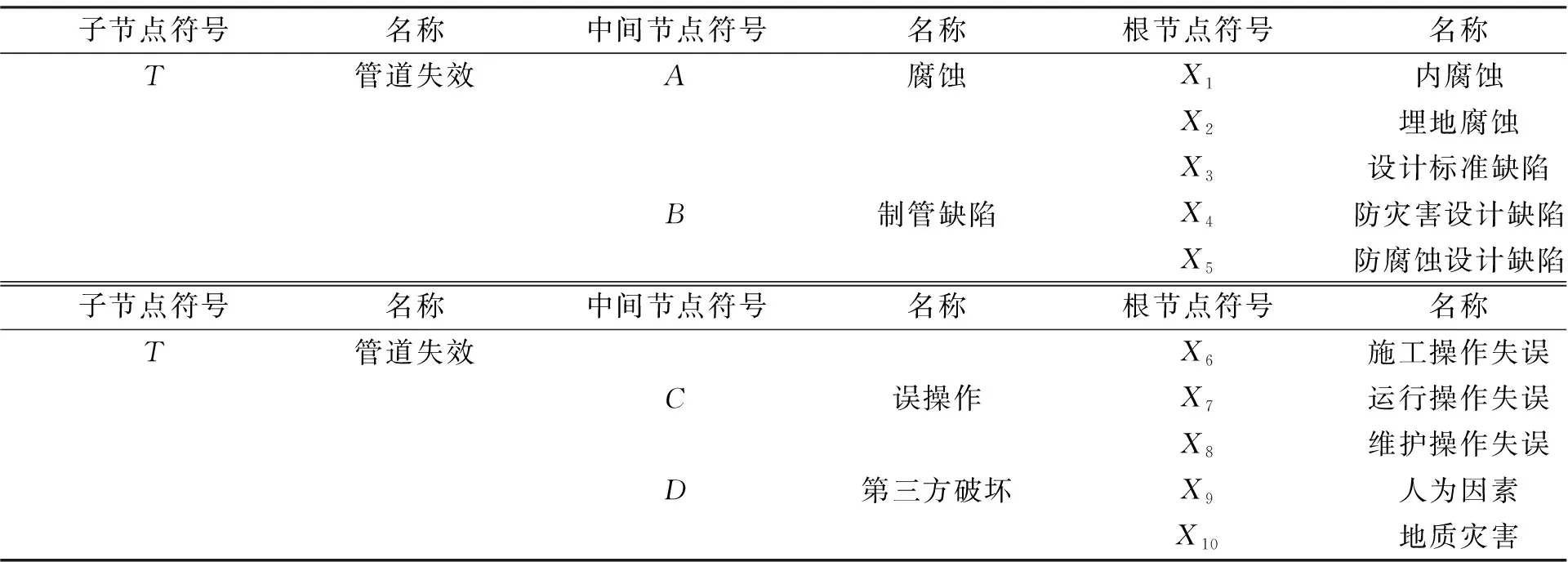
表2 网络中符号对应的名称

利用事故树确定了管道失效风险因素之间的逻辑关系, 通过转化为贝叶斯网络从而确定了管道失效风险模型的网络结构, 下面将论述网络中各个节点参数的设计。

2.2 管道失效风险贝叶斯网络参数的确定

基于已建立的管道失效风险贝叶斯网络模型, 由于节点较多, 参数的复杂度随节点的增加呈指数增长, 且参数在无专家知识经验下很难确定, 采用EM(Expeetation Maximization)算法进行网络参数学习仍存在严重的估计误差问题。为此, 笔者通过引入遗传算法完成贝叶斯网络参数学习, 旨在获取最优的网络参数。

2.2.1 网络模型中的参数

贝叶斯网络参数对应网络中每个节点相对于父节点集的条件概率分布, 是父子节点之间概率依赖程度的一种量化表述。根据图4构建的贝叶斯网络模型, 设其贝叶斯网络为：G={N,υ}, 其中N为管道失效贝叶斯网络模型的网络结构,υ为该模型的网络参数, 则所有参数的集合可表示为υ={θ1,θ2,…,θ10,θA,θB,θC,θD}。对模型中父节点{X1,X2,…,X10}, 由于该集合中每个元素均无父节点, 因此它们的参数{θ1,θ2,…,θ10}可由先验概率{P1,P2,…,P10}表示, 对子节点{A,B,C,D}, 其参数集合{θA,θB,θC,θD}中每个元素代表一组CPT(条件概率表), 各个参数对应的CPT分别如表3、表4、表5和表6所示。

表3 腐蚀节点CPT示意表

表4 制管缺陷节点CPT示意表

表5 误操作节点CPT示意表

表6 第三方破坏节点CPT示意表

2.2.2 管道失效风险似然函数的构建

管道风险贝叶斯网络模型的每个中间节点需要进行似然函数的构建, 但由于节点不唯一, 且节点对应的CPT较为复杂, 为了提高遗传算法获取节点对应CPT数值的效率, 因此需要将管道风险贝叶斯网络模型中的网络节点{A,B,C,D}采取分割方式使其独立化, 将笔者建立的管道风险贝叶斯网络模型G分割为4个独立的网络拓扑结构, 其中, 腐蚀节点A与其对应的根节点{X1,X2}作为一个网络拓扑结构G1, 即求取参数θA时, 观测其父节点数据集{X1,X2}, 制管缺陷节点B、 误操作节点C与第三方破坏节点D分别构建网络拓扑结构的方式同腐蚀节点类似, 利用每个节点参数与其对应数据集之间的似然关系构建似然函数。

(5)

2.2.3 基于遗传算法的参数学习

为获取最优的管道失效模型中的腐蚀、 制管缺陷、 误操作和第三方破坏参数, 将已构建的似然函数作为算法中的适应度函数, 旨在获取最优的网络参数。采用遗传算法对管道风险贝叶斯网络模型参数寻优的详细设计步骤如下。

1) 染色体的编码。集合中的每个元素均在[0,1]区间内, 因此笔者采用二进制小数编码方式, 为了缩短个体长度, 对元素的编码只保留小数位, 精度为小数点后8位, 如0.23, 二进制表示为0.0011101011100…, 则编码为00111010。

2) 种群初始化。在计算前以随机方式生成初始群体, 设置染色体长度为k, 其值取决于条件概率表中参数的个数, 若为4, 则k取32, 若为8,k取64。设置种群规模M, 即每次随机产生M次k位[1-99]的随机数形成初始种群, 种群中每个个体对应一组条件概率分布。

3) 适应度函数。选取最大似然函数L(θ)作为适应度函数F(x), 保留最优个体。

(6)

4) 选择操作。以轮盘赌的方式实现选择操作, 选取优秀的个体并复制到下一代群体中。

5) 交叉操作。选取交叉概率为PC, 笔者采用离散重组式多切点交叉法, 对选定的两个个体P1和P2, 由于每个个体基因长度为8, 因此随机选取k/8个切点, 并交换多个切点之间的子串, 即完成交叉操作。

6) 变异操作。选取变异概率PM, 在种群中选取若干个基因位改变其位值, 由于编码采用二进制, 因此变异过程采用离散变异反转其位值。

7) 终止条件。当连续t代其适应度不再发生变化时, 终止条件判断输出最优网络参数。

3 应用实例

笔者采集了某油田投产日期自1964-2019年的油管线、 气管线、 注水管线、 注剂管线的失效数据作为研究对象。首先, 利用GeNIe贝叶斯仿真模拟软件对油田失效管线数据进行分析； 其次, 利用遗传算法获取该网络模型中的参数； 最后, 结合网络根节点的先验概率以及获得的网络参数进行概率推理得出油田管道失效概率, 通过对比分析验证笔者方法的有效性。通过统计油田管线长度与各个风险因素引发管线失效的次数获得网络模型中根节点的先验概率如表7所示。

表7 根节点先验概率值Tab.7 Prior probability value of root node (次/(km·a))

3.1 GeNIe贝叶斯网络模拟软件

贝叶斯网络仿真工具主要有： BayesiaLab,Analytica,BNT,GeNIe,Netica等。这些仿真工具可根据不同的实际需要选择。目前贝叶斯网络的仿真主要使用Netica和GeNIe仿真工具, 这两种工具能提供直观、 简洁的界面, 在建立贝叶斯网络模型具有很强的便捷性, 软件中内置了许多推理算法。而BNT是Matlab中的一个贝叶斯网络工具箱, 它要求使用者具备一定的编程能力, 而且在内置多种推理算法基础上, 允许使用者编写网络结构、 参数学习和推理算法, 但由于BNT不能提供可视化的图形界面, 使贝叶斯推理结果不能直观地显示。GeNIe是由匹斯堡大学开发的开放式贝叶斯网络模拟软件, 该软件能根据实际需求设置每个节点的状态实现双向推理, 从而准确的判别系统中关键的风险因素。GeNIe软件不仅可以将多元知识图解进行可视化, 建立一种概率知识表达的推理模型, 而且还能贴切的描述管道风险贝叶斯网络模型中网络节点变量之间的因果关系及条件相关关系。软件工具栏中的Chance键用于描述贝叶斯网络节点, Arc键描述节点之间的依赖关系, 因此, 笔者使用GeNIe仿真工具计算油田管道的失效概率。

3.2 管道失效贝叶斯网络参数的获取

针对腐蚀参数θA, 设置染色体长度k=32, 种群M=100, 给定最大遗传代数T=100, 交叉概率PC=0.15, 变异概率PM=0.09, 获取的腐蚀参数CPT如表8所示； 针对制管缺陷参数θB, 设置k=64, 种群为M=50, 给定最大遗传代数T=100, 交叉概率PC=0.3, 变异概率PM=0.13, 获取的制管缺陷参数CPT如表9所示。针对误操作参数θC, 设置k=64, 种群M=50, 给定最大遗传代数为T=100, 交叉概率PC=0.3, 变异概率PM=0.15, 获取的误操作参数CPT如表10所示； 对于第三方破坏参数θD, 设置k=32； 种群M=100, 给定最大遗传代数为T=100, 交叉概率PC=0.15, 变异概率PM=0.1, 获取的第三方破坏参数CPT如表11所示。

表8 设置参数后腐蚀节点CPT

表9 设置参数后制管缺陷节点CPT

表10 设置参数后误操作节点CPT

表11 设置参数后第三方破坏节点CPT

由表8可以看出, 埋地腐蚀X2对管道失效的影响略大于内腐蚀X1的影响, 当二者同时作用于管道, 此时发生失效的可能性最大。似然度的取值体现数据与模型参数的匹配度, 即似然度值越大则说明该参数越真实, 匹配程度越高。腐蚀参数适应度变化曲线如图5所示。从图5中可以看出, 随着参数学习迭代次数的增加, 模型的对数似然度缓慢增加并且渐渐收敛, 此时的参数与真实的网络参数相比差距大。经过40组样本数据后, 其似然度值最大, 匹配程度最高, 最终学习的参数可作为模型中最优参数。

图5 腐蚀参数适应度曲线Fig.5 Corrosion parameter fitness curve

3.3 管道失效结果与分析

3.3.1 管道失效概率推理

为了计算油田管道失效概率, 笔者采用GeNIe软件建立油田管道失效风险贝叶斯网络模型并通过概率推理完成管道失效概率的计算。基于图3设计的管道失效贝叶斯网络结构建立其模型如图6所示, 图6中的网络节点符号名称和有向边与图3一一对应, 其中图6每个网络节点状态为State0代表相应节点事件未发生的概率, State1则代表相应节点事件发生的概率, 将获得的网络参数CPT输入对应网络节点A、B、C、D中, 表7根节点先验概率输入至对应网络节点{X1,X2,…,X10}中, 在系统为Windows 7, 具有8 GByte内存的PC上运行, 其推理结果如图6所示。

图6 GeNIe推理结果Fig.6 Genie’s reasoning results

概率推理得出管道失效风险概率为4.75×10-2次/(km·a), 其数量级处在1×10-3以上, 表明该油田存在一定的事故风险, 因此需要对管道的关键失效风险因素进行分析, 为现场事故和预防提供指导。

3.3.2 管道失效概率分析

为了详细的分析影响管道发生失效的各个风险因素, 利用贝叶斯网络逆向推理和证据更新能力, 将GeNIe设置管道失效状态为已发生(State1=100%), 设置腐蚀状态、 制管缺陷状态、 误操作状态和第三方破坏状态皆为已发生(State1=100%)。由图6可以看出, 埋地腐蚀事件(X2)发生的可能性最大, 其后验概率为5.67×10-2次/(km·a), 施工操作失误(X7)的后验概率仅次于埋地腐蚀, 其后验概率为4.71×10-2次/(km·a), 内腐蚀(X1)失效概率为3.55×10-2次/(km·a), 防腐设计缺陷(X5)失效概率为2.28×10-2次/(km·a)。对风险因素按照失效可能性从大到小排序得到致因链：X2>X1>X6>X7>X8>X4>X3>X5>X9>X10。由此可看出, 影响管道发生失效关键因素为埋地腐蚀、 内腐蚀、 施工操作失误, 因此控制这3项关键因素能有效地降低管道失效风险概率。为了验证改进后模型的精度, 与传统贝叶斯网络模型进行了对比, 其中传统贝叶斯网络概率推理结果如图7所示, 对传统贝叶斯网络和笔者改进贝叶斯网络的概率推理结果进行统计, 对比结果如表12所示。

图7 传统贝叶斯网络概率推理结果Fig.7 Results of traditional Bayesian network probabilistic reasoning

表12 各个模型精度对比

从表12可知, 改进后的贝叶斯网络模型的评估误差为9.70%, 评价精度达到了90.3%, 而传统的贝叶斯网络模型评价精度只达到79.28%, 由此可以看出, 笔者方法所计算的管道失效概率在精度上得到了很大的提升。

4 结 语

笔者针对事故树具有静态属性且无法实现逆推理的缺陷, 提出了一种基于贝叶斯网络的管道失效概率计算方法。首先, 在管道失效贝叶斯网络模型结构方面, 利用事故树分析法建立管道失效事故树模型, 通过事故树与贝叶斯网络的转化确定了管道失效贝叶斯网络模型的结构, 解决了模型结构较难确定的问题； 其次, 在管道失效贝叶斯网络模型参数学习方面, 引入遗传算法改进了贝叶斯网络参数学习以此获取网络中最优参数, 解决了由专家知识经验以及传统参数学习方法获取网络参数存在的估计误差问题； 最后, 将笔者研究的管道风险评估方法应用于实际油田管道风险评估问题, 利用贝叶斯网络仿真软件GeNIe计算得出了油田管道失效风险概率值为4.94×10-2次/(km·a), 并得到了影响管道发生失效的致因链, 通过对比分析验证了笔者方法的有效性。