新分数阶混沌系统的电路设计和同步控制
颜闽秀, 徐 辉
(1. 沈阳化工大学 信息工程学院, 辽宁 沈阳 110142; 2. 工业环境-资源协同控制与优化技术辽宁省高校重点实验室, 辽宁 沈阳 110142)
分数微积分的发展由于其固有的复杂性和缺乏预见性的应用,直到近几十年才应用于一些工程中[1-4].分数阶系统模型能够简洁地描述出许多具有记忆特性的系统和一些复杂的材料,如振荡器[5]、光伏发电模型[6]、超级电容器建模[7]、土壤盐碱化程度分类[8]等.相较于整数阶模型,它能够合理准确地描述现实世界的物理现象,这促进了混沌领域的学者对分数阶混沌理论及分数阶混沌系统模型的探索和研究.
除了经典的整数阶混沌系统的分数阶模型[9-15]被研究外,不同的新分数阶混沌系统被学者提出,Gholamin等[16]提出了一个三维分数阶混沌系统,Zhang等[17]提出了改变一个参数即可产生一至四翼的分数阶混沌系统,Munoz-Pacheco等[18]提出了变量可调的分数阶混沌系统,Zhou等[19]提出了具有复杂共存吸引子的分数阶混沌系统.这些研究成果丰富了分数阶混沌理论和分数阶混沌系统的数量,促进了分数阶混沌系统在工程方面的应用.在混沌领域的研究中,混沌同步控制一直是研究的热点.为了实现驱动系统与响应系统同步,这方面的学者成功地提出了各种控制方案,如PID控制[20]、反馈控制[21]、主动控制[22]、状态观测器控制[23]、投影同步控制[24]、滑模同步控制[25]、鲁棒控制[26]和自适应控制[27-29]等.
本文基于Caputo定义提出了一个新的、仅含一个非线性项的三维分数阶混沌系统,采用预估校正法[30]对系统进行数值仿真,发现它能够产生复杂的双涡卷混沌吸引子.相较于一般的混沌系统,它的结构更为简单,仅含一个非线性项,且易于实现.在通过理论分析和数值仿真验证了系统的混沌特性后,为验证系统实现的可能性,文中设计了系统的分数阶混沌电路并于Multisim中进行模拟实验,实验结果验证了系统实现的可能性.最后针对带有未知参数和扰动的分数阶系统的同步问题,设计了基于自适应的滑模控制器,在扰动上界未知、系统参数不确定的情况下,实现了系统的同步控制.
1 系统模型
本文在研究Silnikov定理的应用时,提出了在Caputo定义下的同量阶分数阶混沌系统,其模型为
(1)
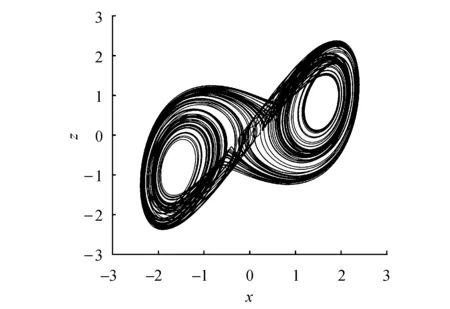
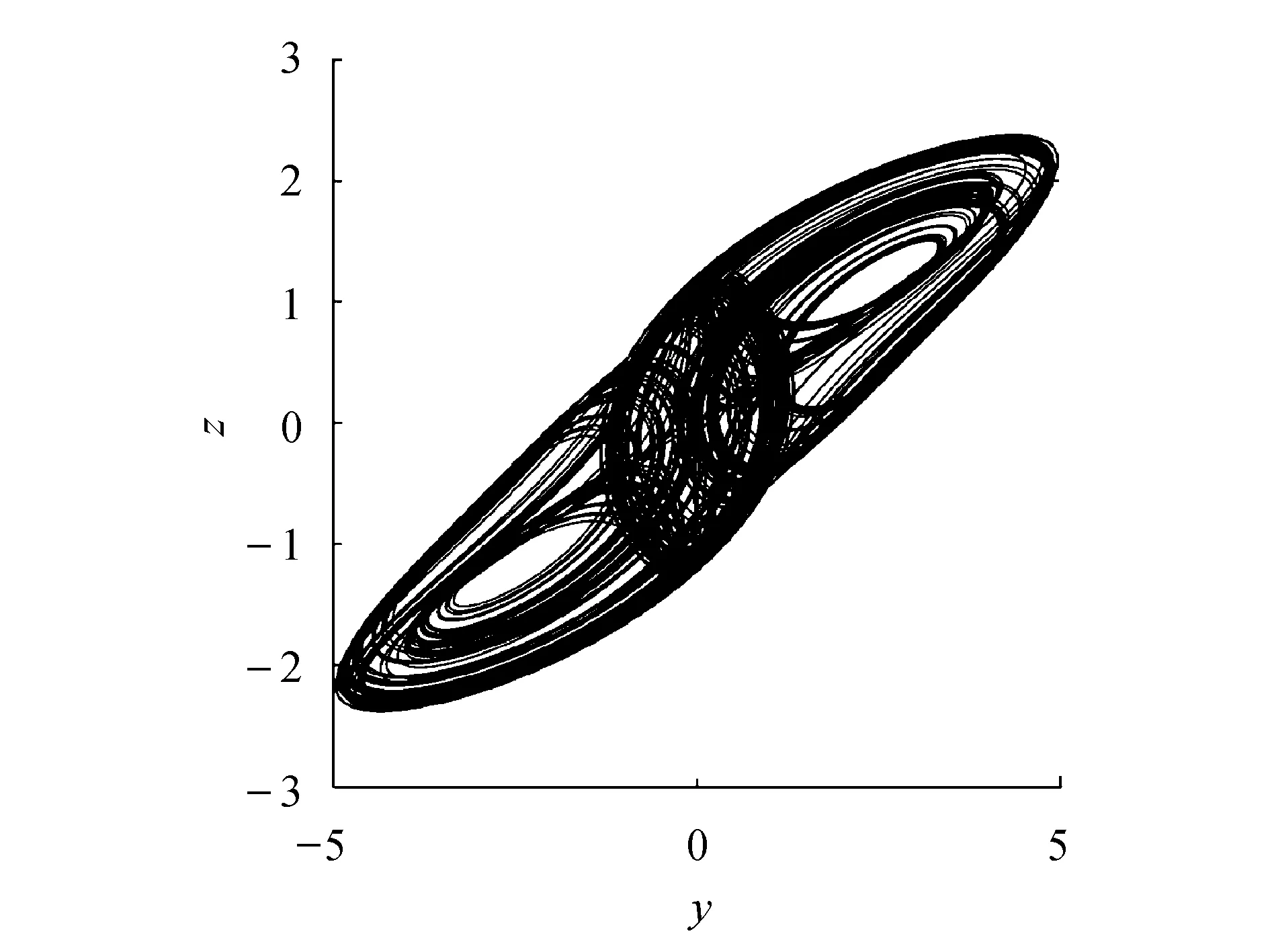
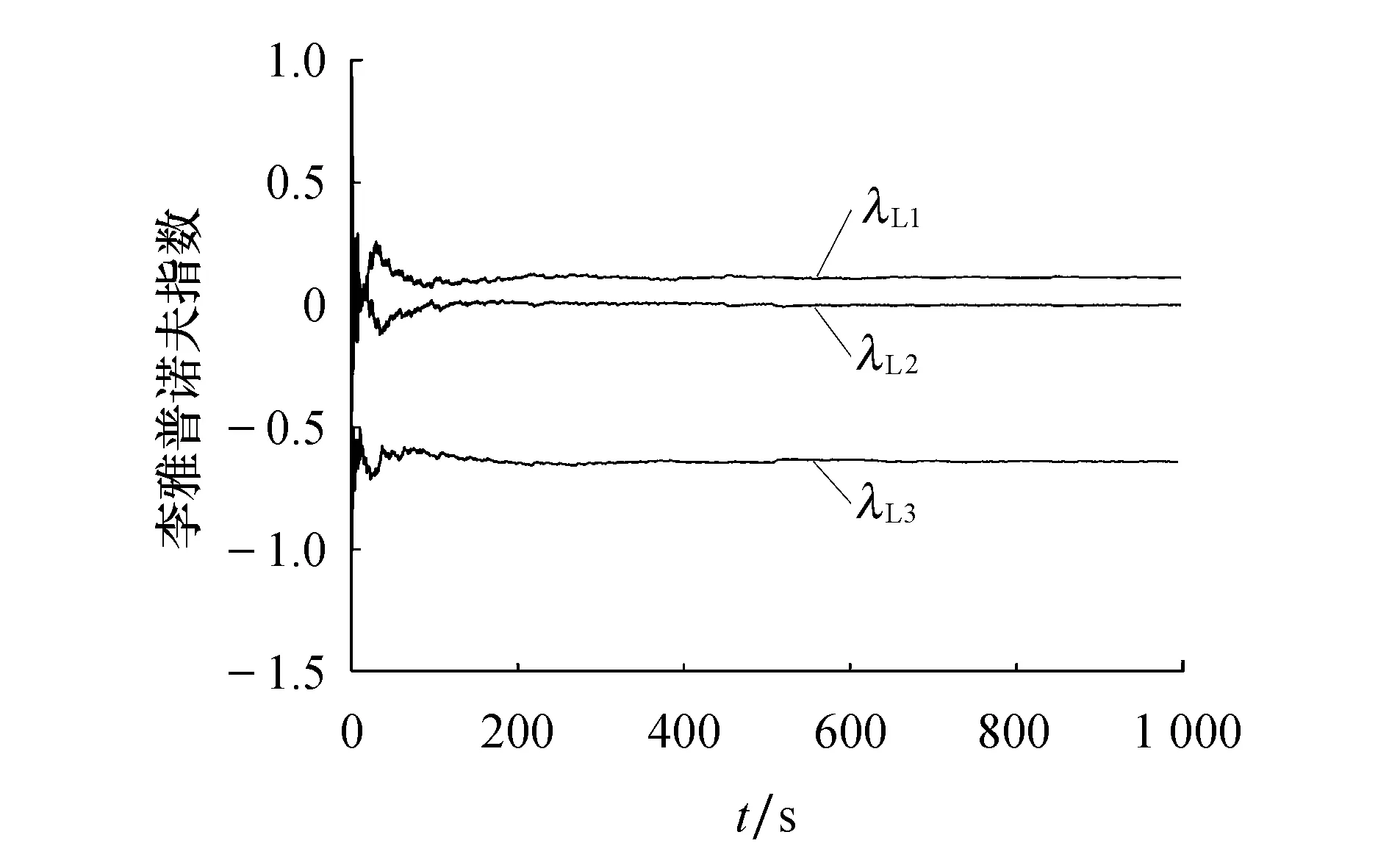
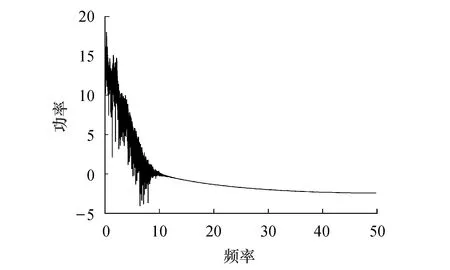
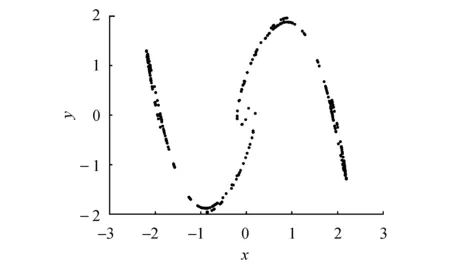
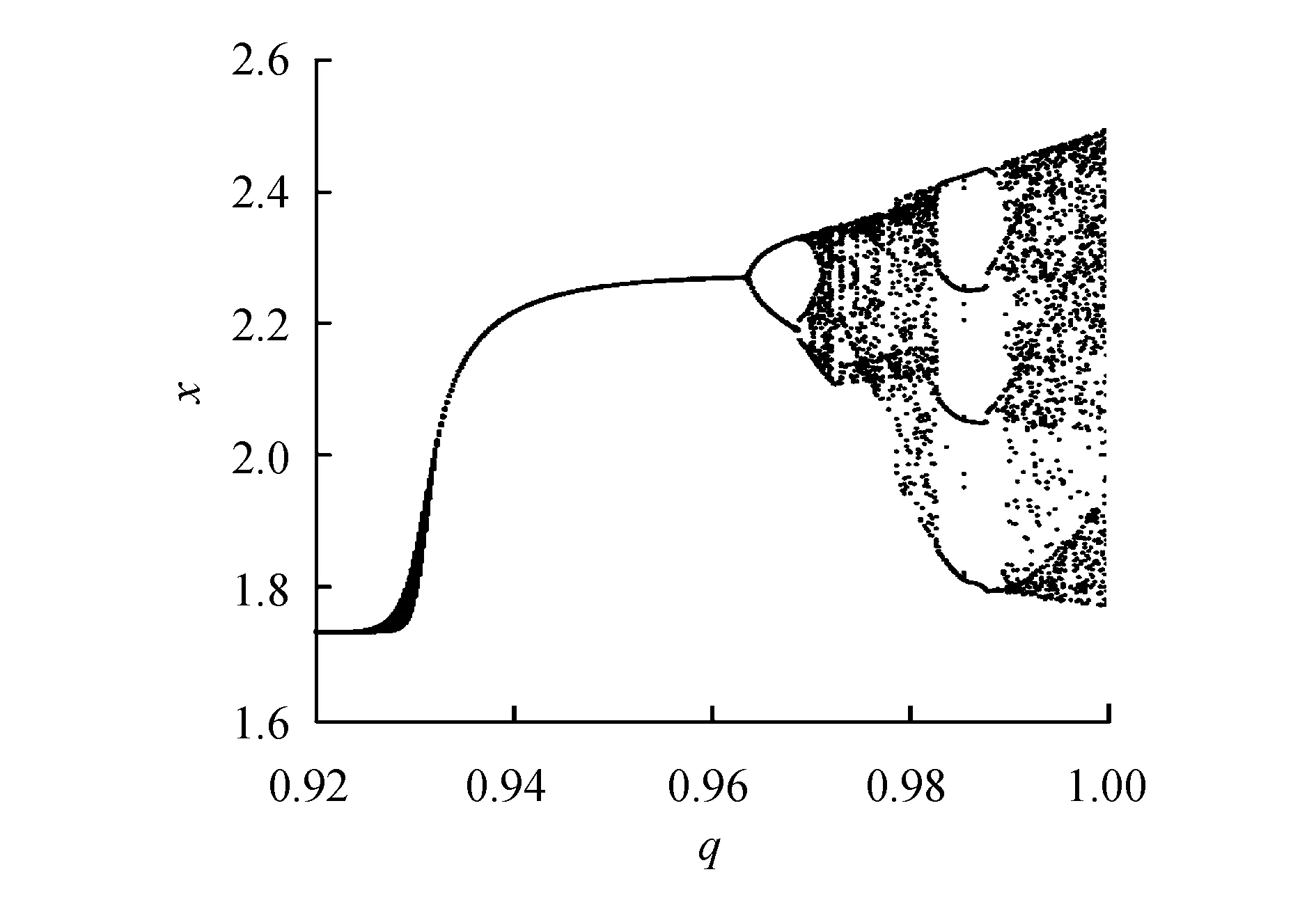
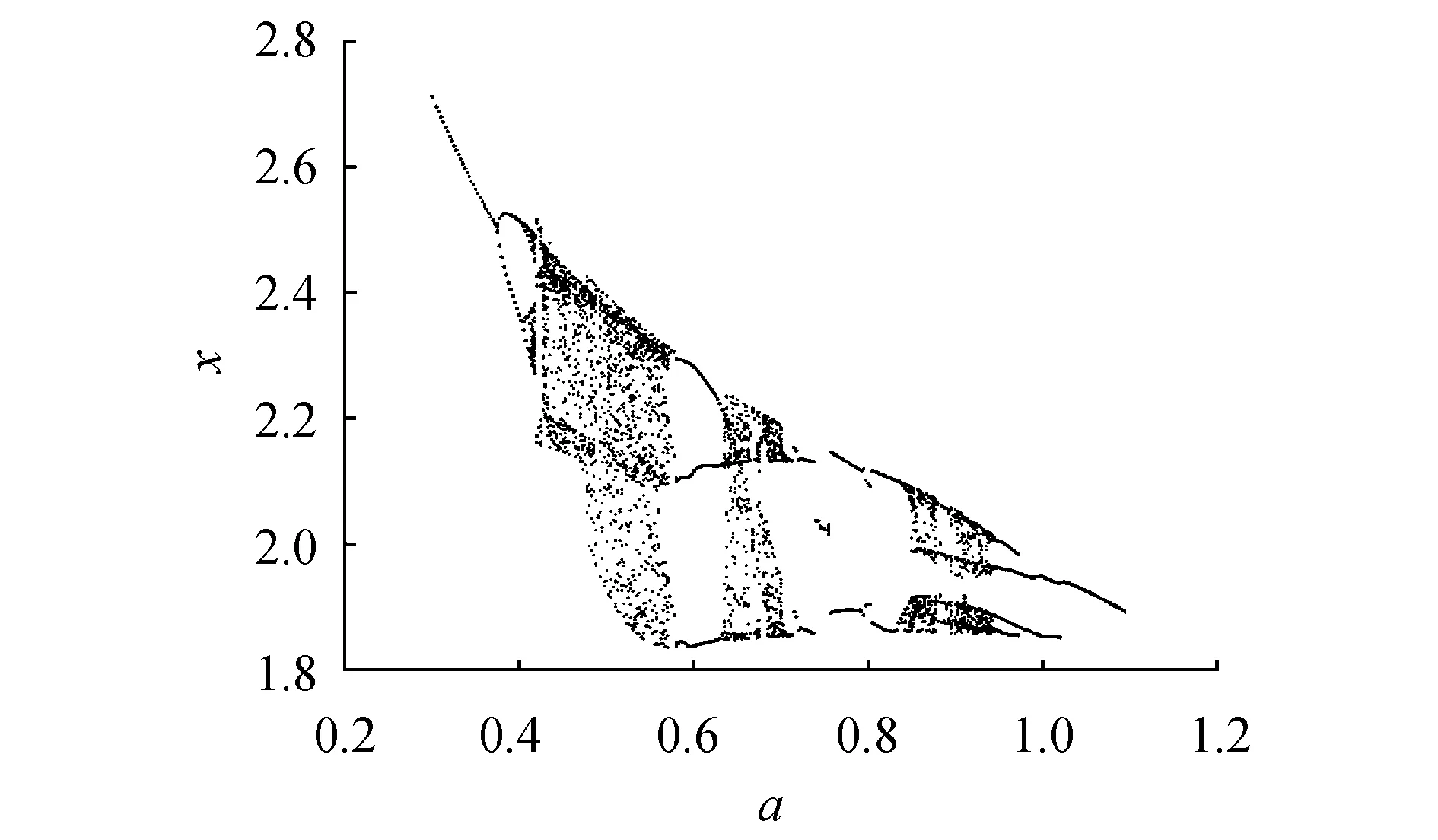
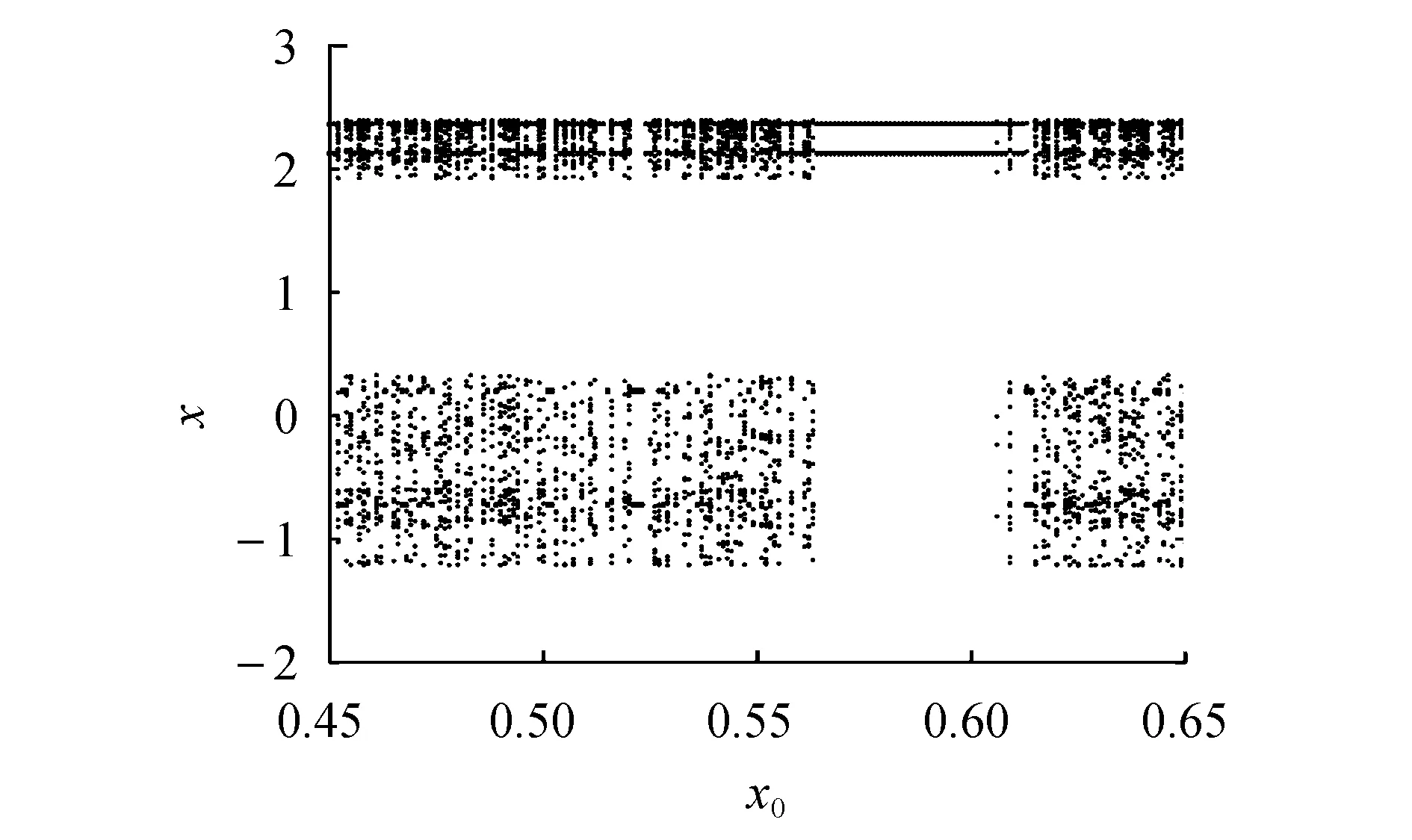
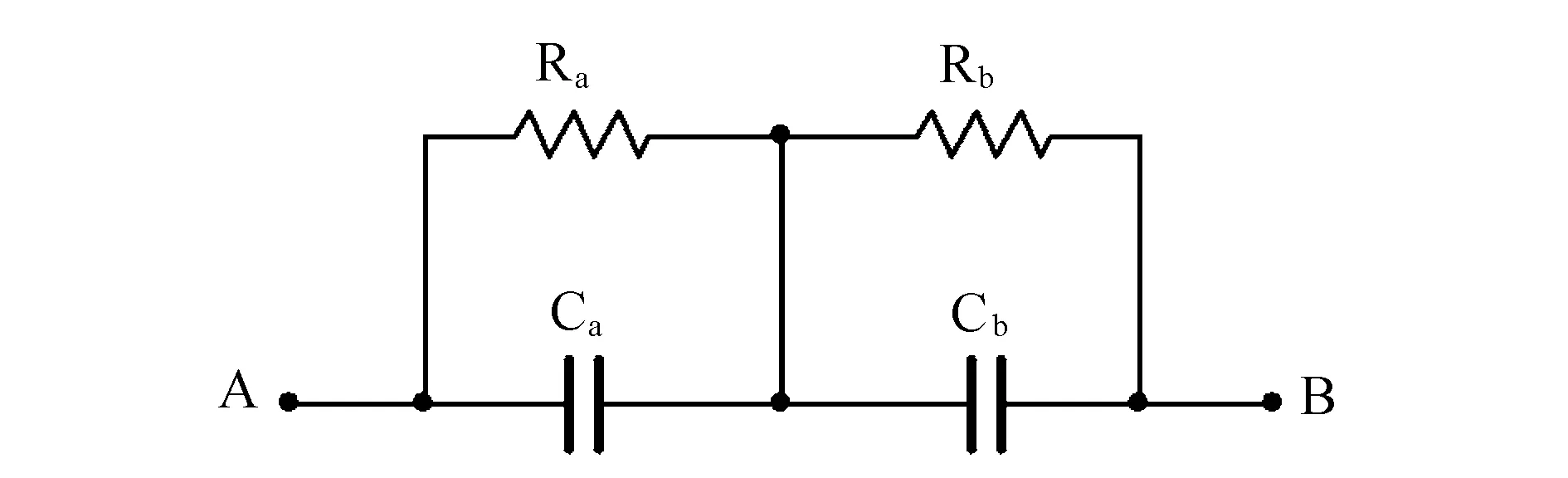
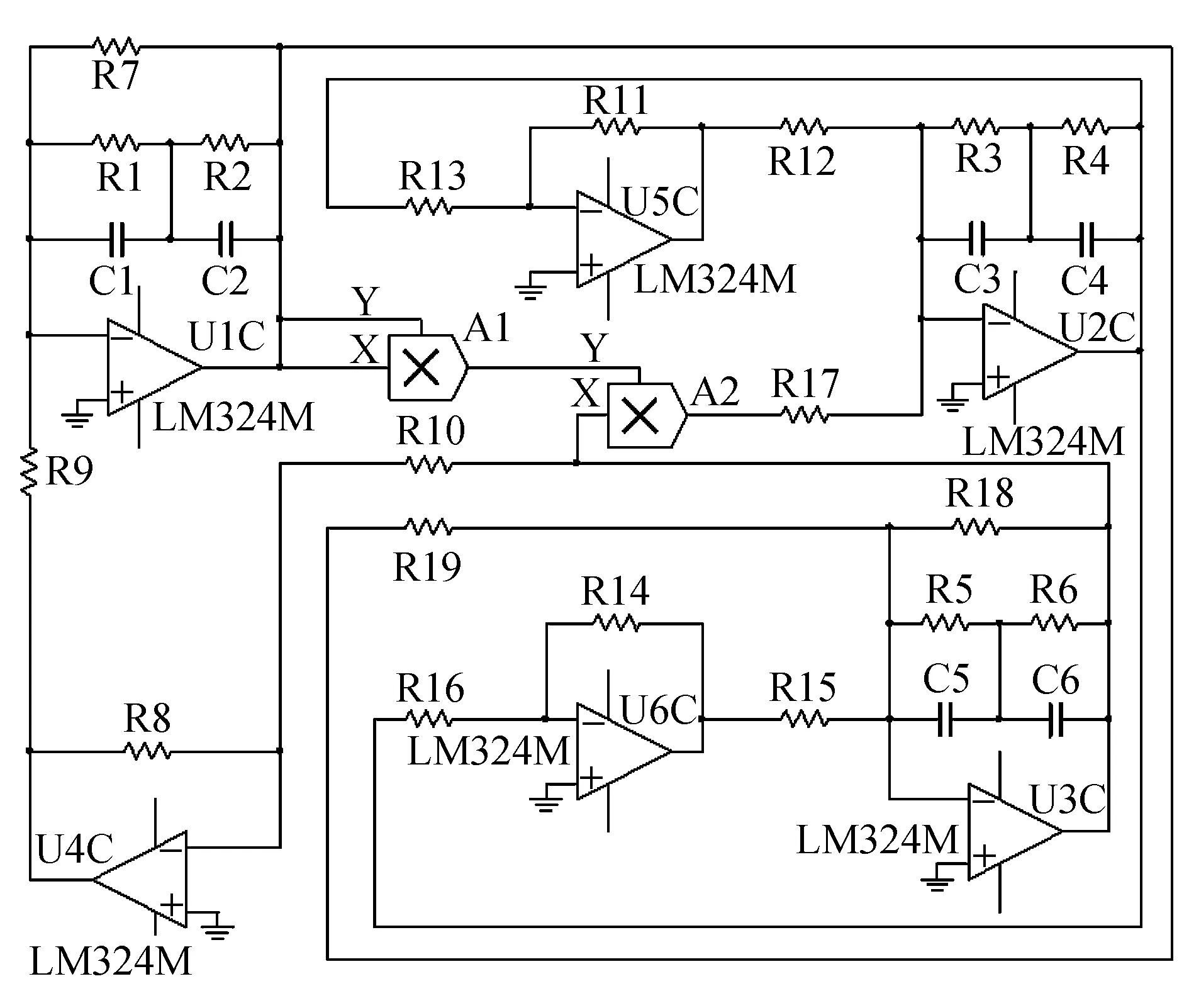
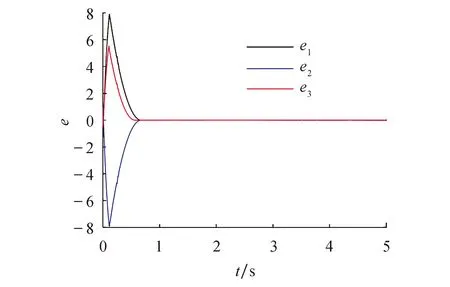
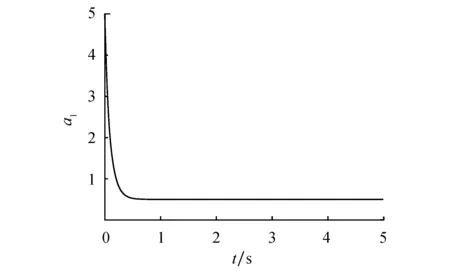
其中:0 图1 混沌吸引子Fig.1 Chaos attractor 图2 x-z相图Fig.2 x-z phase diagram 图3 y-z相图Fig.3 y-z phase diagram 由图1~3可以看出,系统(1)的吸引子的几何形状非常复杂,具有很强的吸引性、复杂的折叠和拉伸轨线,所有轨线被限定在一个特定的区域内. 为验证系统的混沌特性,使用计算机求出分数阶混沌系统的李雅普诺夫指数,得到λL1=0.112 5,λL2=0,λL3=-0.642 1,它们随时间变化的曲线如图4所示. 图4 李雅普诺夫指数Fig.4 Lyapunov exponents 再由下式计算出系统的李雅普诺夫维数DL: (2) 其中j为满足下式的最大整数: (3) 得到: (4) 由上述计算可知,系统的三个李雅普诺夫指数中一个为正,一个为负,另外一个为0,且李雅普诺夫维数为分数,所以表明系统(1)为混沌系统. 为进一步验证系统的混沌特性,利用计算机绘制出系统关于变量x的功率谱(如图5所示)以及x-y平面关于z=0的庞加莱截面图(如图6所示). 图5 功率谱Fig.5 Power spectrum 图6 庞加莱截面Fig.6 Poincare surface of section 从图5和图6可以看出,系统的功率谱是连续谱,没有明显的波峰;庞加莱截面图并不是一条封闭的曲线,而是由密集点构成的具有吸引子轮廓的曲线.这再次表明了系统(1)为混沌系统. 令式(1)等式左边为0,得到: (5) 求解方程组(5),解得方程的三个平衡点,分别为 (6) 代入数据a=0.5,得到: 求得系统的Jacobian矩阵J为 (7) 令det(λI-J)=0,求得其特征多项式为 f(λ)=λ3+A2λ2+A1λ+A0 (8) 其中:A0=ax2+2xz-a-1,A1=x2,A2=a. 将平衡点E1=(0,0,0)代入式(7)进行线性化处理,得到Jacobian矩阵为 (9) 再将平衡点E1代入式(8),求得式(9)的特征值,为λ11=1,λ12,13=-0.75±0.968 2i,由特征值可知平衡点E1是指标为1的不稳定的鞍点. 同理,在平衡点E2、E3处线性化得到Jacobian矩阵为 (10) 求得式(10)的特征值为λ21=λ31-0.894 7,λ22=λ32=0.197 3 + 1.82i,λ23=λ33=0.197 3-1.82i.由特征值可知平衡点E2、E3是指标为2的不稳定的鞍点. 由第2节求出的特征值以及相关的分数阶稳定性理论可知,下式为系统(1)产生混沌的必要条件: q>|argλ22,32|=|argλ23,33|=0.931 3 (11) 系统(1)所选取的阶次q=0.98>0.931 3,符合式(11).为进一步研究阶次q对系统(1)的动力学特性的影响,将系统的阶次q作为系统的分岔参数,绘制并分析系统关于q的分岔图. 固定参数a,令q∈[0.92,1],初始值为(0.5,0.5,0.5),绘制出系统关于参数q的分岔图如图7所示. 图7 q-x分岔Fig.7 q-x bifurcation diagrams 从图7可以看出,在[0.97,0.983]∪[0.99,1]时,系统处于混沌状态.在q=0.963 5处出现叉式分岔,并在q=0.968 4处发生倍周期分岔,最终系统经过一系列的倍周期分岔进入混沌状态.之后在q=0.982 7处发生鞍结分岔,并于q=0.987 5处发生叉式分岔,进而在q=0.988 5处发生倍周期分岔,最后经一系列倍周期分岔系统进入混沌状态. 现在,为分析系统参数a对系统动力学特性的影响,绘制并分析系统关于参数a的分岔图. 固定参数q,令a∈[0.3,1.1],初始值为(0.5,0.5,0.5),绘制得到系统关于参数a的分岔图如图8所示. 图8 a-x分岔Fig.8 a-x bifurcation diagram 从图8可以看出,当参数在区间[0.43,0.573]∪[0.632,0.7]∪[0.85,0.88]∪[0.9,0.94]时,分岔图中出现由密集点构成的区域,系统处于混沌状态. 考虑到分数阶混沌系统(1)中含有x2z这种交叉高阶项时,系统(1)可能对x变量的初始值非常敏感.现在改变x变量的初始值x0绘制分岔图,来确认该模型动力学特性是否依赖于x变量的初始值,实现混沌与周期模态的切换. 固定q=0.98,a=0.5,取初始值(x0,0.5,0.5),其中x0=[0.45,0.65],绘制x0-x分岔图,如图9所示. 图9 x0-x分岔Fig.9 x0-x bifurcation diagram 由图9可知,系统的混沌特性受到变量x初始值的影响.特别地,当x0在区间[0.57,0.62]时,分数阶系统(1)处于周期2模态. 取x0=0.6,则初始值为(0.6,0.5,0.5),此时系统会产生周期2轨道,如图10所示. 图10 周期2轨道Fig.10 Orbit of period 2 由上述分析可知,系统具有丰富的混沌特性. 通过设计分数阶混沌电路进行模拟来判断系统(1)是否具有实现的可能性,并对上述理论分析和仿真结果进行验证.电路将采用线性电阻、运算放大器、模拟乘法器(增益为1)以及图11所示的链型电路.其中模拟乘法器用于实现系统中的非线性项,运算放大器及其相关电阻用于实现加、减运算,链型电路用来实现1/s0.98的单元电路. 图11 1/s0.98的单元电路Fig.11 Unit circuit of 1/s0.98 当分数阶次q=0.98时,1/s0.98的波特图近似式为 (12) 链型电路中,A与B之间的传递函数F(s)为 (13) 式中:C0为单位参数,取C0=1 μF,H(s)=F(s)C0=1/s0.98,将式(13)与式(12)对比可以得到 (14) 由式(14)可知: (15) 通过以上对q=0.98阶单元电路的分析,用Multisim设计实现该电路的原理图如图12所示,图中U1=x,U2=y,U3=z. 图12 分数阶混沌系统电路原理 Fig.12 Circuit schematic diagram of fractional order chaotic system 复频域中分数阶混沌系统的方程表示为 (16) 将式(16)与式(1)比较,可作如下取值: (17) 基于上述数据进行电路模拟,模拟结果如图13和图14所示. 图13 U1-U3相图Fig.13 The phase trajectory of U1-U3 图14 U2-U3相图Fig.14 The phase trajectory of U2-U3 从图13和图14可以看出,电路模拟结果与上文数值仿真结果一致,表明分数阶混沌系统具有实现的可能性. 将系统(1)作为驱动系统,并写成如下形式: (18) 其中参数a=0.5,阶次q=0.98.取响应系统为 (19) 式中:a1为a的估计参数;ui为自适应滑模控制器;ri为干扰;i=1,2,3. 定义同步误差ei=yi-xi,未知参数估计误差ea=a1-a.由式(19)减去式(18)得到误差系统为 (20) 为便于滑模控制器的设计,作下面的假设. 假设1:干扰有界,但是未知,即|ri|≤di,di未知. 设计滑模面函数为 (21) 定义Di为扰动上界di的估计值,其估计误差为edi=Di-di,设计Di的自适应律为 (22) 由于常数的q阶Caputo导数为0,因此对于干扰上界的误差,有 (23) 针对未知参数,设计其自适应律为 (24) 式中:控制参数k2>0.最后设计自适应控制器为 (25) 式中:fi=-(Di+k1|ei|μ)sgn(si)-k3si,i=1,2,3,4;控制参数k3>0. 定理1在干扰上界的自适应律式(22,23),参数自适应律式(24)以及自适应控制器式(25)的作用下,响应系统(19)将与驱动系统(18)实现同步. 证明构造如下的李雅普诺夫函数: 对其求q阶的分数阶导数得到 (27) 将式(21,24)代入式(27)得 (28) 将扰动估计误差edi=Di-di、误差系统(20)、控制器(25)代入式(28),得到 (29) 计算式(29),并对其进行放缩: (30) 令Ti=-|si|+sisgn(ei),有下式成立: (31) 由式(31)可知 Ti=-|si|+sisgn(ei)≤0 (32) 假设1中|ri|≤di,又因为si≤|si|,所以可得 siri-di|si|≤0 (33) 联立式(30,32,33),可得 (34) 综上所述,定理得证. 为验证所设计的控制器具有可行性和有效性,本文采用预估校正算法并使用Matlab进行数值仿真.取驱动系统的初始值为(0.8,-0.5,0.4),响应系统的初始值为(-0.2,0.5,-0.1),并取干扰r1=0.5sint,r2=sint,r3=cost,估计参数a1=5,控制参数ki=20 (i=1,2,3),μ=0.5. 基于上述数据进行模拟仿真,同步误差的仿真结果如图15所示,参数a1的识别过程如图16所示. 图15 同步误差Fig.15 Synchronization error 图16 参数a1的辨识过程Fig.16 Identification process of parameter a1 从图15可以看出,系统的同步误差很快趋于0,主从系统实现了同步.从图16可以看出,响应系统的估计参数在较短的时间内达到稳定且趋于主系统的参数a=0.5.这验证了本文所设计的自适应滑模控制器以及自适应律的可行性和有效性. 本文提出了一个仅含有一个非线性项的新三维分数阶混沌系统,通过系统的相轨迹图、李雅普诺夫指数谱、功率谱、庞加莱截面、平衡点的稳定性以及系统关于分数阶次和参数的分岔图等来分析系统的动力学特性.紧接着,设计了系统的分数阶混沌电路并进行模拟实验去验证系统的可实现性.最后研究了带有扰动以及未知参数的分数阶系统的同步和参数识别问题,设计出合适的自适应滑模控制器以及未知参数和扰动的自适应律.基于上述研究结果得出如下结论: 1) 提出的三维分数阶系统是混沌系统,结构简单,仅含有一个非线性项,具有丰富的混沌特性. 2) 当该系统的阶次或参数变化时,系统的混沌特性更为丰富. 3) 该系统具有电路实现的可能性,在保密通信等领域具有潜在的应用价值. 4) 设计的自适应滑模控制器、参数的自适应律以及扰动的自适应律是切实可行且有效的,不需要知道扰动的上界即能实现混沌系统的同步控制以及系统不确定参数的辨识,更符合实际的工程应用.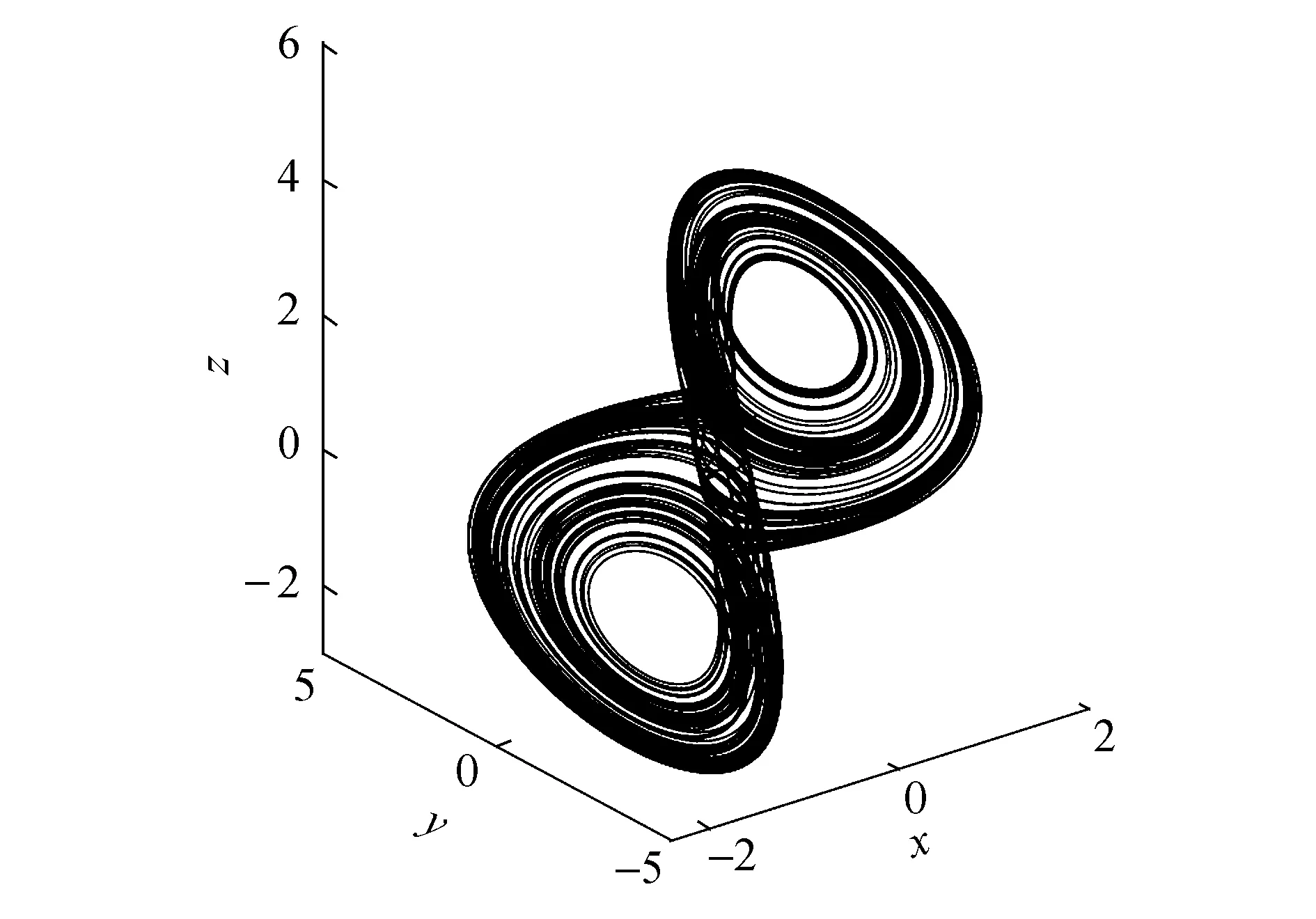
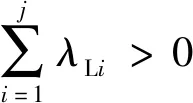
2 平衡点及其稳定性
3 分岔图

4 电路设计
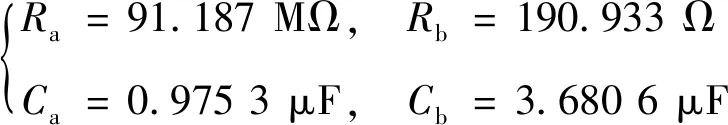


5 自适应滑模同步控制
5.1 滑模控制器及参数自适应律的设计

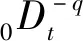
5.2 同步仿真实验
6 结论

