斜交角对带翼墙框架式地道桥受力性能影响
王建省 李泽洲 陈晓强
(北方工业大学土木工程学院,北京 100144)
随着城市规模的不断扩大,为满足道路交通安全和铁路提速的要求,需要采用立交形式改变铁路与公路道口平交现状[1]。其中,箱涵结构具有构造简单、施工周期短、成本低、力学性能好等特点,故修建框架式地道桥是解决此类交通干扰问题的有效方法[2]。正交式地道桥已被广泛应用,其研究体系也比较完备,董锐等探究覆土厚度对框架式地道桥受力性能影响,认为随着顶板覆土厚度增加,框架桥最大竖向变形和最大应力均有变小的趋势,但最大横向变形和最大轴向变形基本没有变化[3];杨功勤等对地道桥简化图式的静力、动力特性的分析,归纳出地道桥设计的一般规律[4];Shinae Jang将DLV技术运用于地道桥检测中,使用SDLV传感器确定潜在损伤位置[5]。然而,在桥梁设计中,会因为桥位、线形等因素将桥设计成斜交桥[6-10]。斜交框架地道桥的受力情况复杂, 不仅有弯矩、剪力、 轴向力, 还有扭矩作用, 且扭矩随着斜交角度的减小而变得不可忽略[11-15]。以下对斜交带翼墙框架式地道桥力学性能进行研究。
1 工程概述
河北省某下穿既有公路单孔斜交地道桥,洞口两侧均配有翼墙结构。桥位所处地层较为稳定,由上至下可划分为4个大层,如表1所示。

表1 地层特性
该桥为整体现浇钢筋混凝土闭合框架结构,净跨径为8 m,净高2.8 m。通道中心全长39.4 m,全宽9.3 m,顶板、底板和立墙厚度均为0.65 m,翼墙厚度为0.5 m。框架桥上部通行铁路,下部为车辆和行人通道,闭合框架轴线与道路中线夹角为68°,基本参数如图1所示。框架桥采用C30混凝土,主筋采用HRB335,土体容重γ=18 kN/m3,内摩擦角φ=35°。由于该结构较大,故选取其中一个沉降块进行研究,如图2所示。
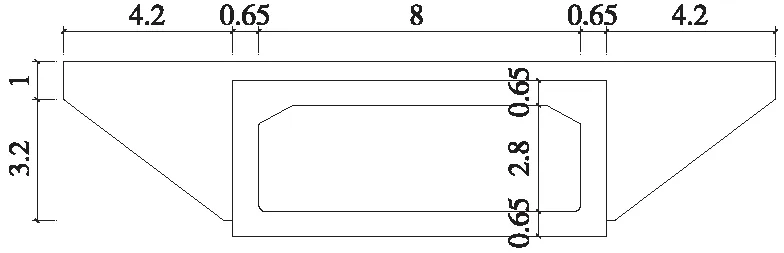
图1 框架箱涵断面(单位:m)
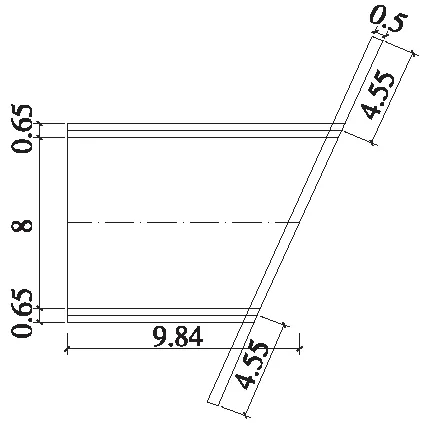
图2 箱涵平面示意(单位:m)
2 有限元分析
2.1 本构关系
使用Midas Civil有限元软件建立框架桥模型,分析在恒荷载和移动荷载作用下斜交角对地道桥内力、应力、位移等力学参数的影响。为了考虑横向剪应力的影响,基本假设采用厚板理论,由材料的本构关系,有
{F内}=[D]{ε}
(1)
其中
{F内}=[({N}T{M}T{Q}T)]T
{ε}=[{E}T{χ}T{φ}T)]T
[Dt]、[Df]和[Ds]分别为中面内力与中面变形,弯曲内力与弯曲变形,横剪力与剪切变形之间的弹性矩阵。[D]为内力与变形之间的弹性矩阵。当受温度影响时,假设单元平均温度变化为T,则温度产生一个初应变{ε0},式(1)变为
{F内}=[D]{ε}-[D]{ε0}
(2)
2.2 模型建立
结构采用板单元建模,截面选取长宽均为0.1 m的实腹矩形截面。由于梁单元弯矩为单向,正交桥在建模过程中选取梁单元或板单元差异不大;而斜桥的横向弯矩不可忽略,选取板单元更为合理。板单元的划分和控制节点的选取如图3、图4所示,规定1号~5号节点分布方向为横向,与之正交的方向为纵向。为了方便研究斜交角变化对地道桥的影响,模型斜交角度依次增加15%,分别为45°、52°、60°、68°和78°。
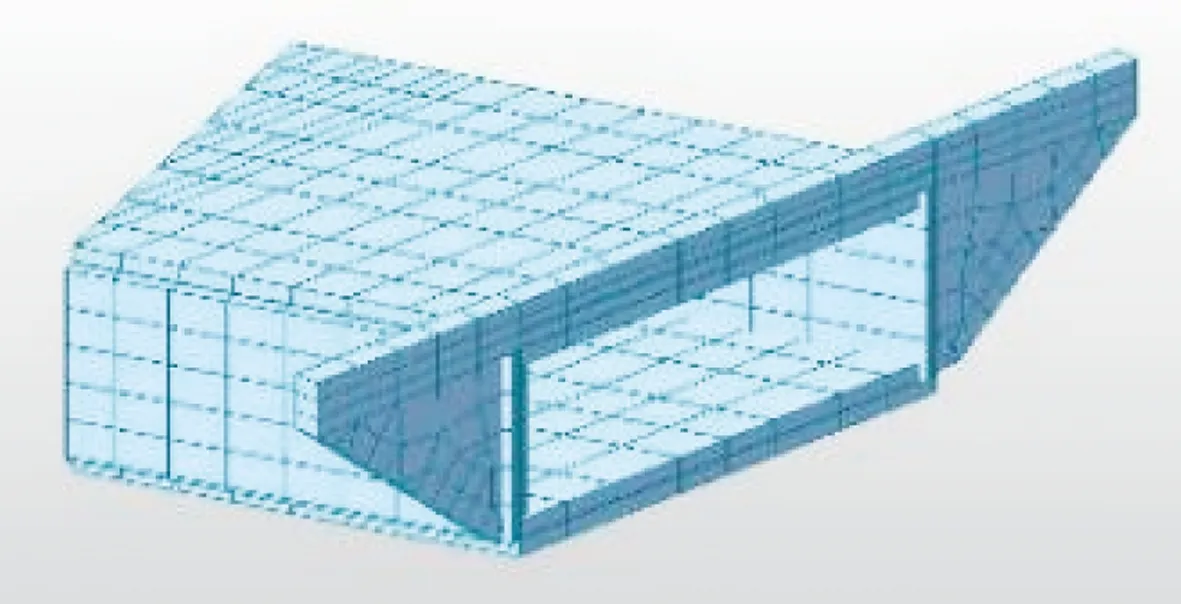
图3 模型三维效果
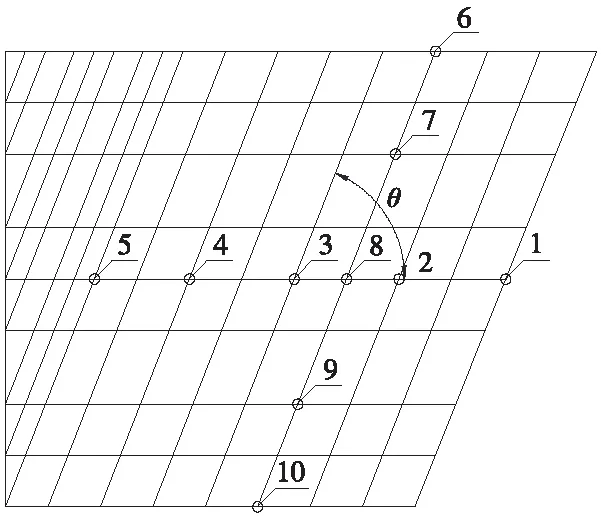
图4 顶板单元划分和关键节点选取
结构自重、顶板覆土压力、台后土压力和翼墙土压力计为恒荷载;台后活载和车辆荷载计为活荷载,荷载分布如图5所示。其中,台后土压力按梯形荷载考虑,有
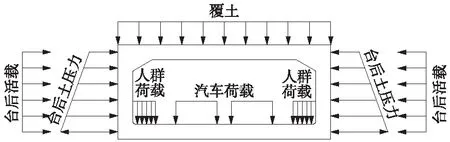
图5 荷载分布示意
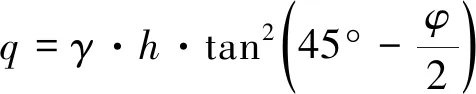
(3)
式中,q为单位面积的台后土压力;γ为土体容重;h为计算点到土体表面的距离;φ为土体的内摩擦角。
2.3 数值分析结果
(1)斜交角对内力的影响
在工程设计中, 地道桥顶板为主要受弯、剪、扭构件,其设计最为关键。图6中,顶板1号~5 号控制节点的横向弯矩随斜交角的增大而减小;图7中,顶板6号~10号控制节点的纵向弯矩随斜交角增加而增大,1号、5号、6号、10号控制节点由于分布在板边缘,曲线变化幅度较小。
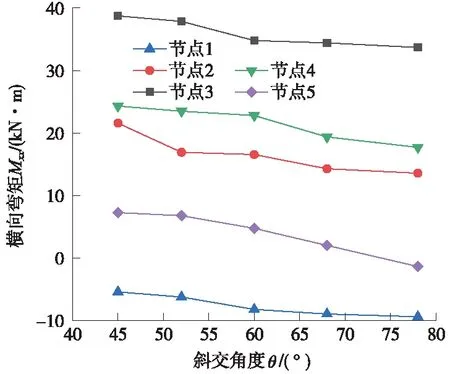
图6 顶板控制节点横向弯矩曲线
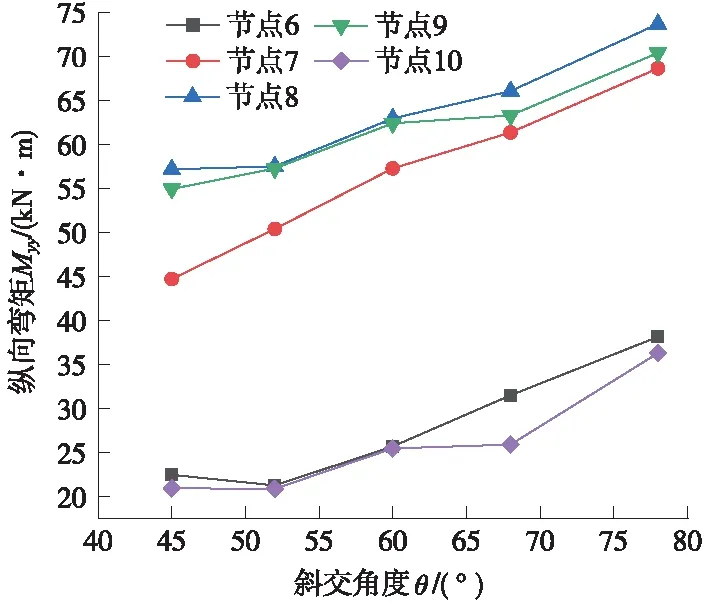
图7 顶板控制节点纵向弯矩曲线
图8、图9中,移动荷载引起的横向弯矩峰值主要集中在跨中车道面附近,板边缘弯矩较小,与图6、图7中曲线跨中节点和边缘节点竖向分离较大的结果相符。对比图8、图10,发现顶、底板右侧钝角区域的弯矩值大于锐角区域。通过与其余各角度云图对比发现,不论斜角度如何变化,顶、底板钝角区域的内力总是大于锐角区域,且不同角度下的底板横、纵弯矩峰值出均现在钝角区域,斜交角在68°左右时,钝角区域弯矩值最大,其余各角度弯矩值依次减小。表2中,控制节点的横向弯矩变化幅度随角度增加而减小,节点2处于跨中,弯矩减小幅度明显大于板边缘节点4。表3中,控制节点的纵向弯矩变化幅度随角度增加而增大,在68°左右弯矩增加幅度放缓。
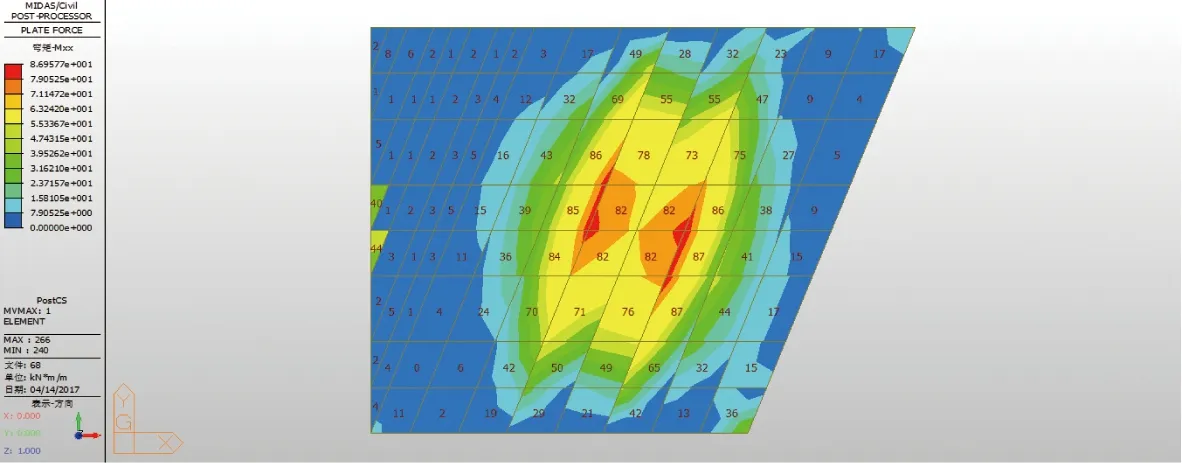
图8 68°顶板横向弯矩云图
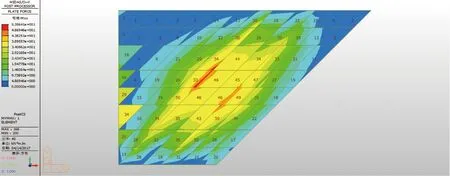
图9 45°顶板横向弯矩云图

图10 68°底板纵向弯矩云图
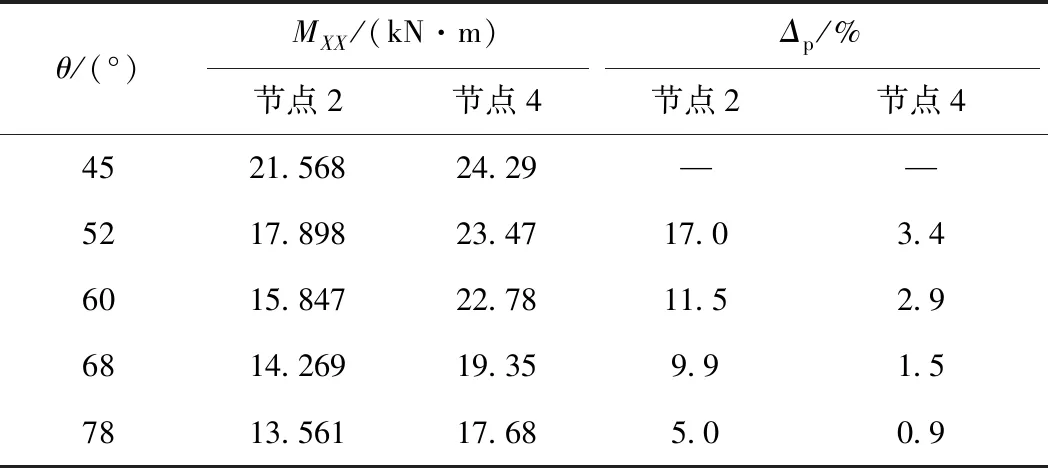
表2 斜交角变化下控制节点的横向弯矩
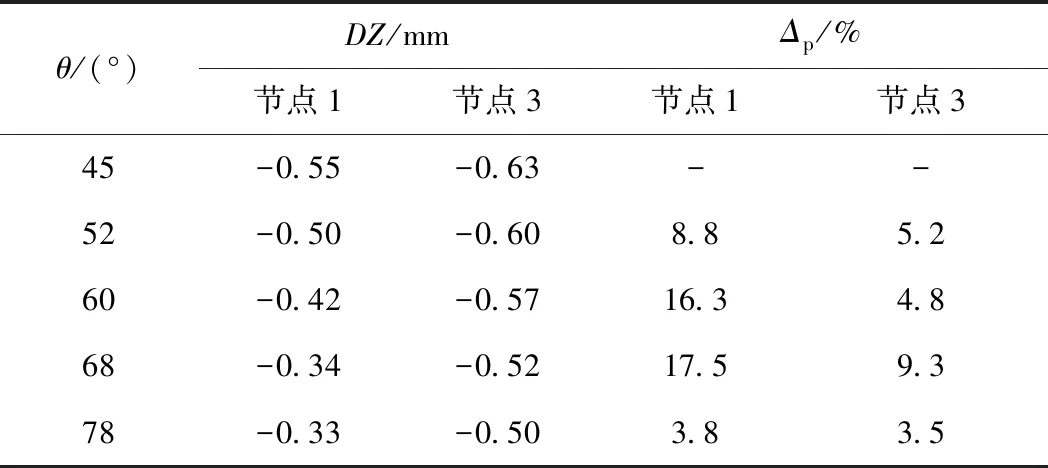
表3 斜交角变化下控制节点的竖向位移
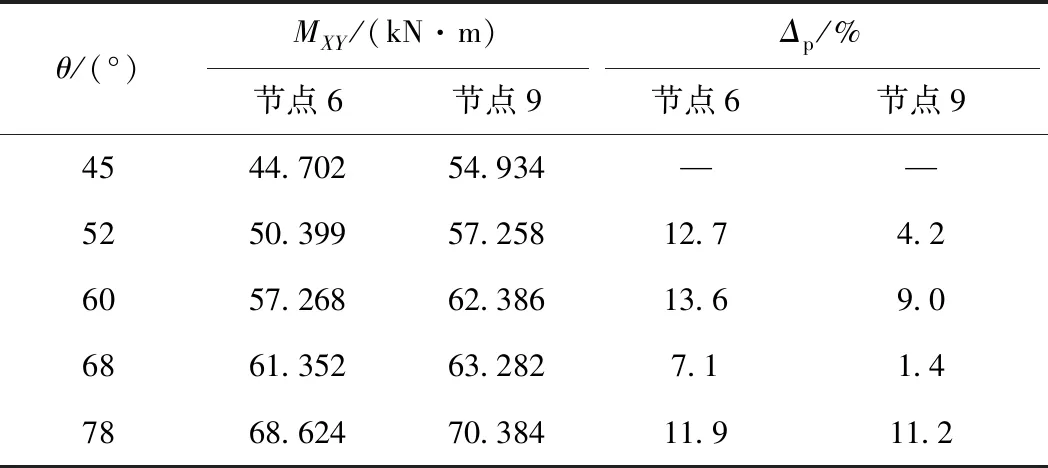
表3 斜交角变化下控制节点的纵向弯矩
(2)斜交角对位移的影响
图11中,各曲线分离明显,不同斜交角度下的竖向位移值差距较大,随着斜交角的增大,顶板控制节点的竖向位移减小,跨中节点为位移最大处。
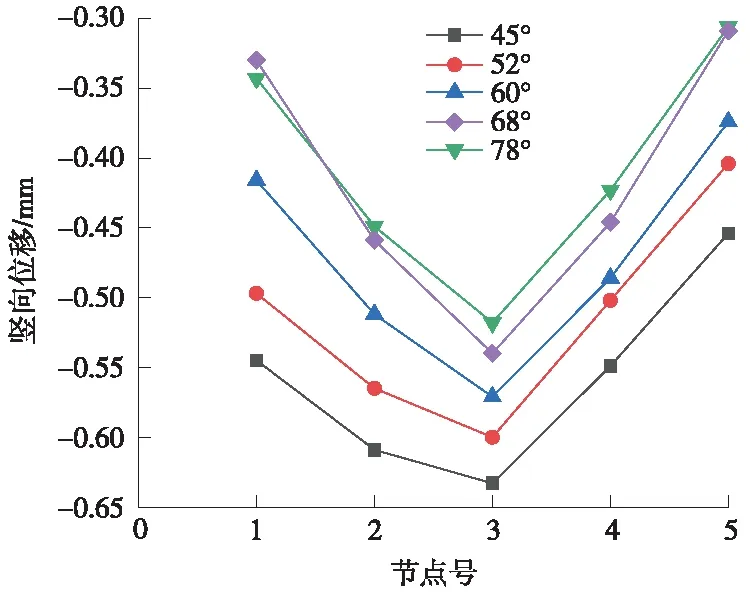
图11 顶板控制节点的竖向位移
表3中板边缘节点1的竖向位移的变化幅度整体大于跨中节点3,且两节点在68°附近位移值变化幅度最大。
(3)斜交角对应力的影响
图12、图13中,顶板的四角和与立墙接触的部位均出现了应力集中现象,出现较大的拉应力,顶板的上部和下部的应力集中现象随角度增大有所缓解。图14中,顶板上部各控制节点第一主应力随斜交角增大而减小,且1号控制节点拉应力值较大,因其处在板边缘且为翼墙连接处。

图12 45°顶板第一主应力云图
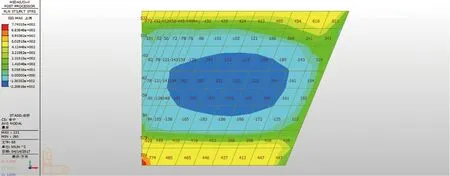
图13 68°顶板第一主应力云图
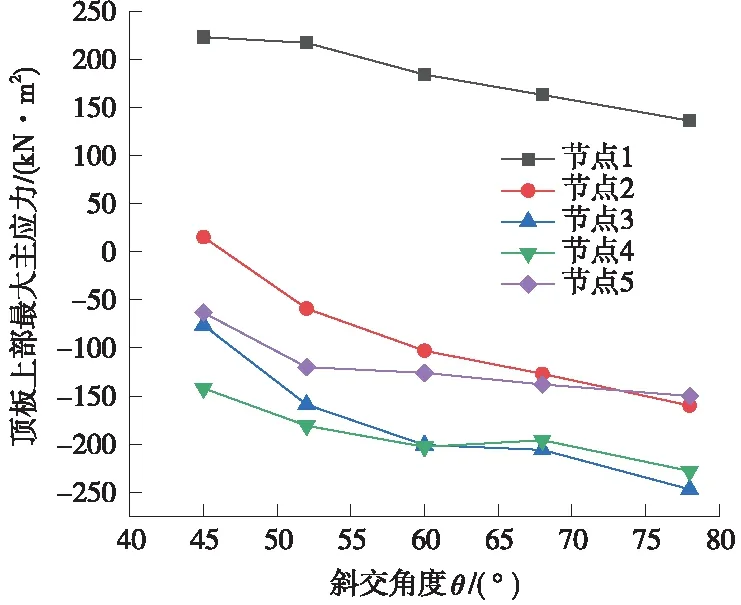
图14 顶板上部的最大主应力
(3)斜交角对洞口翼墙的影响
翼墙作为一个能够承受背后山体土压力、稳定边坡、保护道路免受落石与雪崩等危害的防护承载结构,在箱涵结构中具有不可代替的作用。
图15中,翼墙左侧等值线为深蓝色部分,为翼墙与较短立墙连接的部位,出现应力集中现象,最大主应力为负值。在该区域选取控制节点,绘制图16中的曲线。不难看出,该节点最大主应力全部为负值,且应力的绝对值随斜交角增大而减小,变化幅度较大。
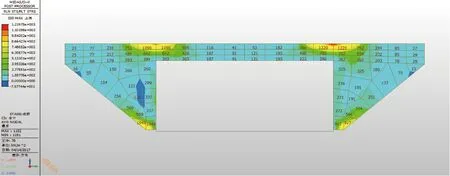
图15 78°翼墙第一主应力云图
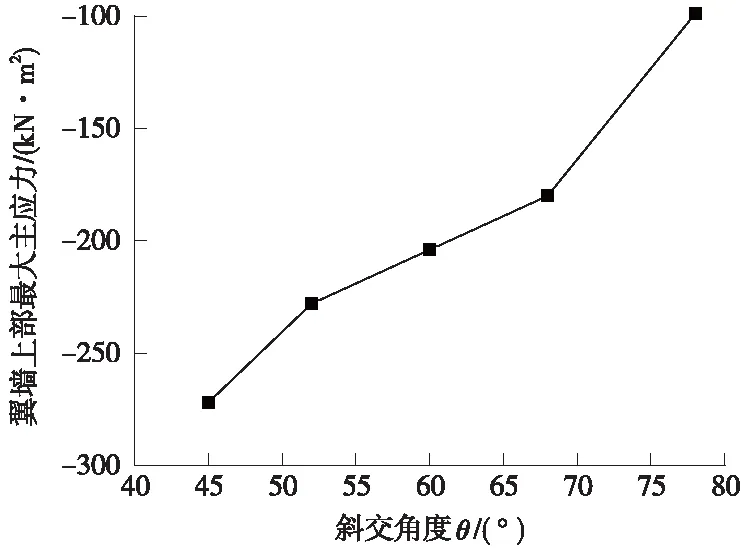
图16 翼墙上部最大主应力
3 结论
通过Midas Civil软件研究了斜交角对带翼墙的闭合箱涵内力、位移、应力的影响,在所给参数范围内,得出以下结论。
(1)顶板的横向弯矩随斜交角度增大而减小,纵向弯矩随斜交角增大而增大,不论斜角度如何变化,顶板钝角区域的内力总是大于锐角区域,且形状不对称。顶、底板钝角处会产生较大的负弯矩, 其方向并不等同于跨径方向。在配筋时可增设钝角加强钢筋,加强钢筋的直径应相当于主筋, 其间距以10~20 cm为宜 。
(2)顶板的竖向位移值随斜交角的增大而减小。顶板上部最大主应力随斜交角增大而减小,翼墙与立墙连接部位的控制节点最大主应力,随斜交角增大而减小。
(3)顶板最大主应力和竖向位移随斜交角增大平均减幅较大,分别为43.5%和8.65%,这说明斜交角较小时桥体的刚度会明显降低,在设计小角度斜交桥时应考虑额外加固措施。

