基坑分段开挖下部盾构隧道纵向变形规律研究

安伟博

(中铁工程设计咨询集团有限公司济南设计院，济南 250022)

随着我国地铁大规模建设和城市化进程加速，上跨既有盾构隧道的基坑工程越来越多[1-2]。对工程措施和下部盾构隧道变形规律进行研究尤为重要。

已有许多学者进行相关研究，陈郁通过用Mindlin弹性半空间应力解和弹性地基梁理论得出隧道隆起的定量计算公式[3]；欧雪峰利用Mindlin解和Pasternak双参数地基模型，得出考虑降水时隧道的隆沉变形规律[4]；黄栩认为在计算隧道纵向变形时，Kerr地基模型最为精确，Pasternak模型次之，Winkler模型的计算结果最不理想的结论[5]。然而，理论方法多适用单次简单开挖，很难对复杂多次分段开挖问题进行计算和假定分析，局限性很大。

孙波等通过Plaxis软件对上跨、临近隧道或车站基坑工程的开挖模拟，认为合理选择基坑开挖顺序、减少基坑单次暴露长度对控制隧道和车站变形具有重要作用[6]；汪鹏程等通过Flac3d等软件模拟了上跨盾构隧道基坑开挖过程，认为坑底加固、抽条放坡开挖+板锚支护、分段开挖+“板凳桩”加固对减小隧道隆起变形效果明显；魏纲等通过对临近和上跨隧道的基坑工程的实际监测，得出隧道横截面变形为椭圆形的结论[7-14]。通过众多学者的研究，虽然也得出了一些隧道变形相关的结论，但是这些变形结论更多局限在最大位移值或者是隧道横断面方向[15-17]，对复杂的基坑分段开挖时下部盾构隧道的纵向变形规律的研究相对较少，而搞清楚这个问题则显得尤为重要。

基坑同隧道平面关系越接近平行，卸载引起的隧道纵向变形范围越大，越有利于研究隧道的纵向变形规律。但多数研究中，基坑和隧道的关系多为邻近[18-19]或近似垂直相交[20-21]，小角度长距离斜交的情况较为少见。以徐州市轨道交通1号线杏山子车辆段出入段线基坑小角度斜跨路窝站-杏山子站区间右线盾构隧道为例，通过数值软件对分段开挖基坑下盾构隧道的纵向变形规律进行研究。

1 工程概况1.1 项目背景

徐州市轨道交通车辆段出入段线基坑与1号线路窝站-杏山子站区间右线平面交角约为16°，相交里程K0+737.335。K0+697.000～K0+757.000段为叠交核心区。核心区内出入段为单洞双线矩形框架结构，宽10.92～13.07 m，高6.31 m。路杏右线盾构隧道外径为6.2 m，内径为5.5 m，错缝拼装结构，基坑开挖前，盾构已掘进完毕并即将进入铺轨阶段。核心区基坑深8.5～9.2 m，坑底与盾构隧道竖向净距约3.0 m。因基坑同隧道小角度斜交，若采用直立开挖，会有较长范围的围护桩嵌固过浅，故拟采用放坡法开挖，坡率为1∶2。

1.2 水文地质

地层从上至下依次为1-1杂填土、2-5-2粉土、2-2淤泥质黏土、2-5-2粉土、2-3-3黏土、2-5-3粉土、2-4-3粉质黏土、2-4-4粉质黏土、5-3-4黏土层等，坑底主要位于粉土和粉质黏土层中，盾构隧道主要位于5-3-4黏土层中。地下水类型为孔隙水，位于地面以下0.7～2.7 m。核心区的平、纵断面分别见图1、图2。

图1 核心区平面

图2 核心区地质纵断

2 数值模拟分析研究

开挖卸载问题是三维问题，具有时间和空间效应。数值模拟则非常适宜处理此类多方案、多工序、多时序的复杂三维问题。采用Flac3d有限差分软件进行全过程的三维模拟。

2.1 计算模型

采用Flac3d进行计算。土体、岩体、明挖隧道采用实体单元模拟，土体和岩体为弹塑性、服从摩尔库伦准则，明挖隧道为弹性；盾构管片采用壳单元进行模拟，取为弹性模型。模型不进行地下水的模拟。模型尺寸为200 m(基坑纵向)×150 m(基坑横向)×80 m(深)。模型四周施加各向的水平法向约束，模型底部施加竖向法向约束，模型顶面为自由边界。计算模型见图3，核心区60 m基坑与下部隧道的空间关系见图4。

图3 计算模型

图4 核心区60 m基坑与下部隧道空间关系

2.2 模型参数

根据勘察报告可得本次数值模拟的地层和结构参数，见表1。

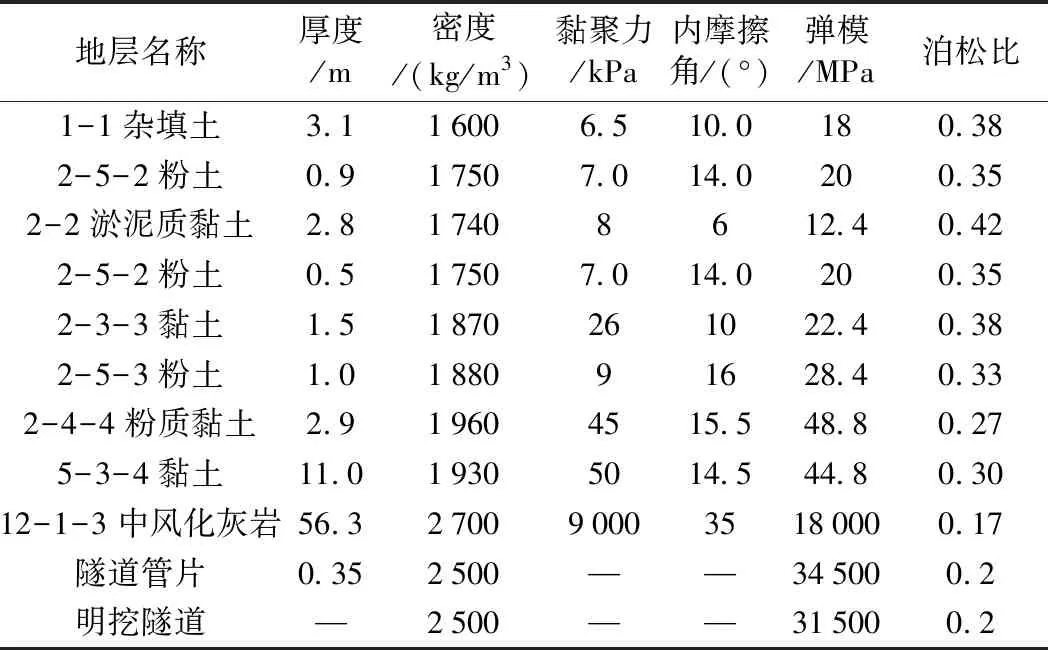
表1 数值计算模型参数取值

2.3 数值计算过程

模型建立后，首先施加重力荷载，形成初始地应力；再模拟开挖、施工下部盾构隧道，并计算至平衡；对土层、隧道单元位移清零；进行洞内预压重或基坑开挖工作直至结束。土体开挖采用Flac3d中的空(Null)模型模拟。

2.4 数值模拟计算(盾构隧道洞内无压重)

分核心区60 m为3段：大里程20 m(左段、K0+737.000～K0+757.000)、中心里程20 m(中段、K0+717.000～K0+737.000)、小里程20 m(右段、K0+697.000～K0+717.000)。由于叠交段基坑深8.5～9.2 m，故各段基坑均分5层开挖。各段基坑开挖到底后先施工明挖隧道结构，再进行下一分段开挖。具体划分为7个方案，见表2。

表2 洞内无压重各模拟方案

(1)具体方案介绍

上述7个方案按照各分段不同的开挖顺序划分，可分为4个组合。

①方案一：目的是分析叠交核心区整体一次性分层开挖时隧道的变形情况，以便与其他方案的计算结果进行对比。

②方案二和方案三：均为向同一方向的顺次开挖，分别为从左向右开挖和从右向左开挖。

③方案四和方案五：均为先开挖两侧分段后开挖中间分段。

④方案六和方案七：均为先开挖中间分段后开挖两侧分段。

(2)计算结果分析

各方案盾构隧道出现最大隆起时，竖向位移云图分别见图5～图11；各方案隧道的最大竖向位移值见表3；各方案隧道最大竖向位移值在隧道纵向的出现位置见图12。

图5 方案一隧道最大竖向位移云图

图6 方案二隧道最大竖向位移云图

图7 方案三隧道最大竖向位移云图

图8 方案四隧道最大竖向位移云图

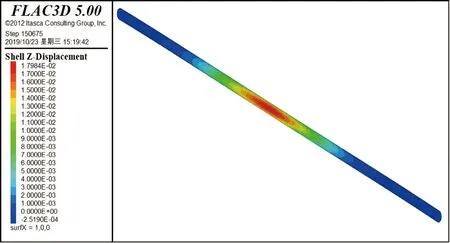
图9 方案五隧道最大竖向位移云图

图10 方案六隧道最大竖向位移云图

图11 方案七隧道最大竖向位移云图

表3 各方案隧道最大竖向位移值对比 mm

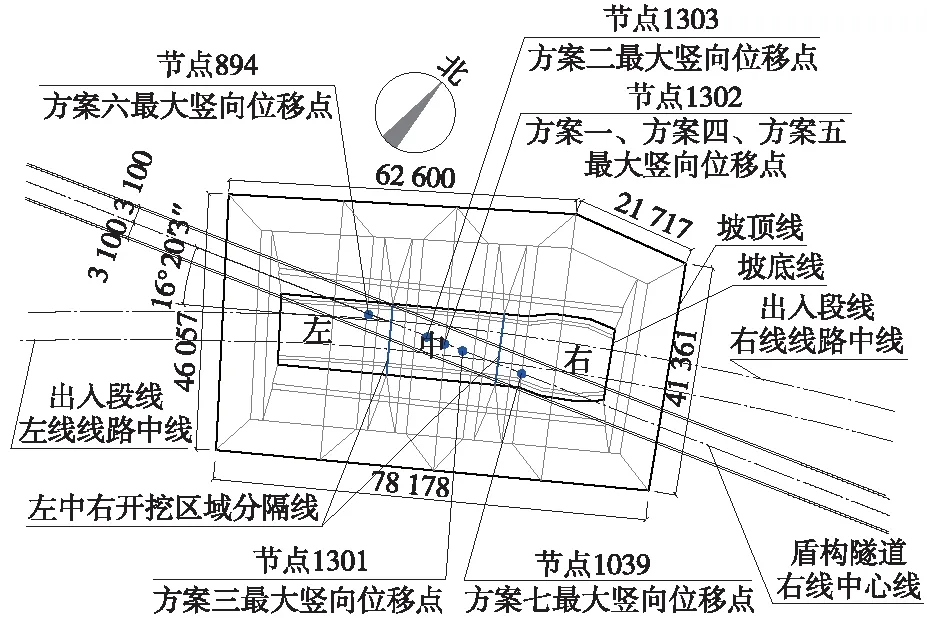
图12 各方案最大竖向位移点平面位置(单位：mm)

各方案盾构隧道最大竖向位移值隧开挖进程的变化趋势及其相互间的对比关系见图13。

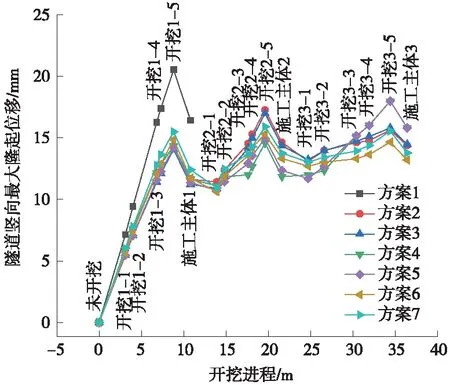
注：①开挖a-b,a取值1、2、3，分别代表各方案先开挖段、次开挖段、后开挖段。以方案一举例，1代表60 m的叠交核心区；以方案二举例，1代表左段、2代表中段、3代表右段。②开挖a-b,b取值1、2、3、4、5，分别代表各开挖段从上至下第1、2、3、4、5层土。以方案一举例，1代表核心区60 m的第一层土；以方案六为例，1代表各分段的第一层土。③施工主体1、2、3，分别指各方案先开挖段、次开挖段、后开挖段处主体结构。以方案一举例，1代表核心区60 m范围内全部主体结构；以方案六为例，1代表中段范围内的主体结构。④水平轴不是单纯的竖向深度或纵向长度，同时有土层竖向深度和各分段先后叠加的含义，重在展示整个开挖过程的时空趋势。图13 各方案隧道最大竖向位移变化趋势对比

从图5～图11、表3中可以得出如下结论。

①整体开挖时盾构隧道最大隆起位移值和隧道隆起范围均明显大于分段开挖时。开挖分段越多越短，盾构隧道的最大隆起位移值越小，隧道隆起范围越小。

②最大竖向隆起位移均出现在隧道拱顶。

③先开挖核心区中段基坑时，开挖对隧道隆起的影响范围最小。

④以最大隆起位移作为主要标准，方案六最优，即最优开挖顺序为中段、左段、右段。

从图12中可以得出如下结论。

①最大隆起位移在盾构隧道纵向出现的位置与开挖顺序呈现比较明显的相关性。方案一、方案四、方案五最大竖向位移点出现位置相同，其位置基本对应基坑中心；方案二和方案三最大竖向位移点出现位置，相对靠近基坑中心并呈左右对称关系；方案六和方案七最大竖向位移点出现位置相对远离基坑中心，并呈左右对称关系。

从图13中可以得出如下结论。

①开挖分段个数与趋势图中位移峰值个数相同。

②首段开挖时，各方案隧道最大隆起位移随开挖深度线性增加，整体一次性开挖时斜率明显大于分段时。次段和后段开挖时，隧道最大隆起位移随开挖深度近似线性增加，斜率明显小于首段开挖时。

③施工出入段线主体后，隧道隆起位移均有比较明显的回落，回落数值与主体质量、回填土质量呈正相关。

④施工各主体后的第一次开挖，隧道隆起位移均出现未升反降的特点。说明后次开挖对前次开挖段下部隧道的隆起变形进行适当平衡，是隧道整体性的体现，但是调整幅度有限。后次开挖段的变形速率明显小于前次开挖段，也证明隧道整体性对最大隆起位移的舒缓作用。根据计算结果进行统计，此作用对位移的单向调整比率约为5.71%。

2.5 数值模拟计算(盾构隧道洞内预压重)

以方案六为基础，研究洞内压重激励对基坑分段开挖卸载时下部盾构隧道变形规律的影响。

(1)洞内预压重方案介绍

盾构隧道洞内压重范围为路杏区间右线右DK2+365.000～右DK2+455.000，共90 m，范围为根据盾构隧道和出入段线放坡基坑的平面位置关系综合确定。每延米洞内压重分别取0，50，100，150，200，250，300，350，400 kN(共9种)。洞内预压重且计算至平衡后，方可按照方案六进行开挖施工。

(2)计算结果分析

①不同压重级别下隧道沉降情况

预压重工况时，不同压重级别下隧道最大沉降值和隧道最大沉降值随压重量的变化曲线分别见表4和图14。

表4 各压重级别时盾构隧道最大沉降值对比

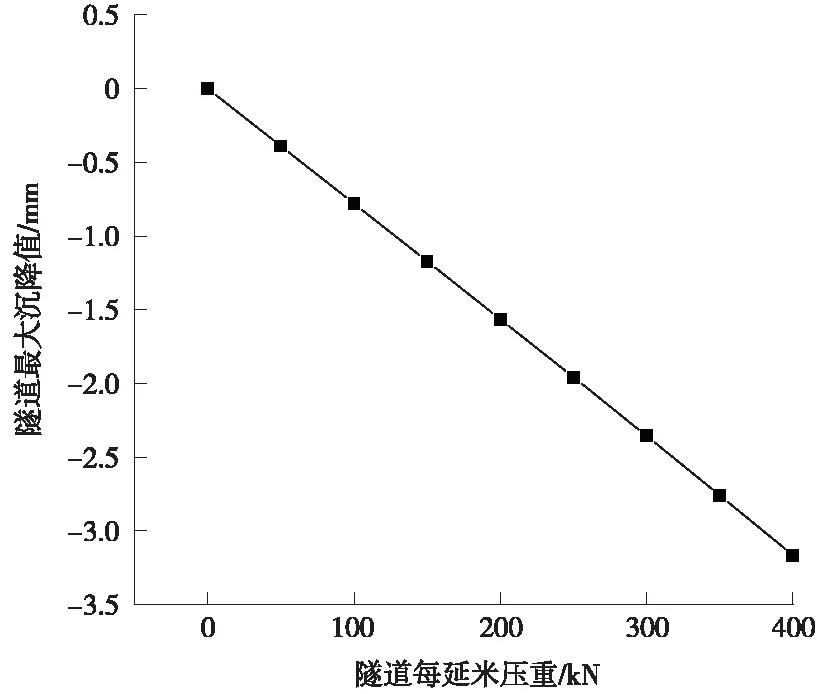
图14 预压时隧道最大沉降值随压重变化趋势

②盾构隧道最大隆起位移变化趋势

不同压重下，隧道最大竖向位移随开挖进程的变化趋势见图15；压重状态与无压重状态下隧道最大竖向位移值差值随开挖进程的变化趋势见图16。

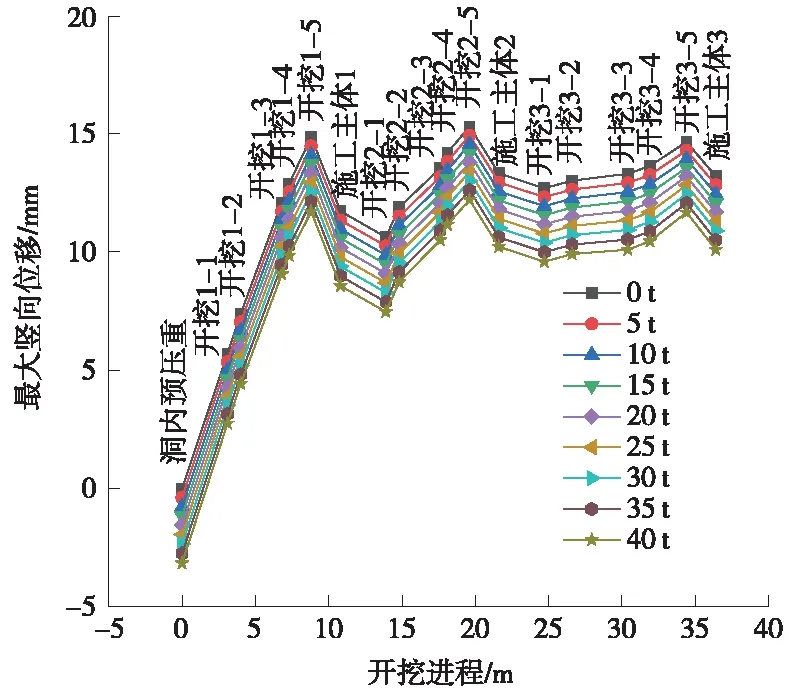
图15 各压重级别时隧道最大竖向位移变化趋势

图16 隧道最大竖向位移差值变化趋势

从图14和表4中可以得出如下结论。

①隧道沉降值随预压质量增加而线性增大。

②就本工程而言，使盾构隧道隆起减小1 mm，需要压重约126.4 kN。由于耗费相对较大，综合考虑造价、对全线工期影响、便宜性等因素后，选择50 kN作为本工程的洞内压重。

从图15可以得出如下结论。

洞内预压并未改变隧道隆起的变形趋势；不同压重级别时隧道的变形曲线呈近似平行关系。

从图16可以得出如下结论。

随着开挖的进行，洞内压重对隧道最大竖向位移的影响呈波浪形，压重越大波浪形特征越明显。这种特性属于压重激励时，隧道的整体性对各相邻部分结构彼此变形的调整，根据计算结果进行统计，调整比率约在5.71%。此数值与卸载方案时得出的结论高度对应。

3 结论

(1)基坑分段越短，下部盾构隧道的最大隆起位移值越小，同时隧道隆起范围越小。开挖分段个数与隧道隆起位移峰值的个数相同，其分段越均匀，峰值大小越接近。

(2)应优先开挖叠交核心区中段基坑，而非两侧基坑。

(3)隧道纵向各相邻部位对彼此变形的单向调整比率约为5.71%。

(4)分段开挖时，盾构隧道最大隆起点出现位置呈现规律性：中段先开挖时，最大隆起点位置位于次开挖段；中段次开挖时，最大隆起点位置位于中段靠近先开挖段部分；中段后开挖或整体一次性开挖时，最大隆起点位置均位于中段基坑中部。可在一定范围内，利用上述规律，通过调整开挖顺序，可选择让最大竖向隆起位移出现在隧道相对健康的位置，或环境和自身风险相对较低的位置。