中低速磁悬浮列车-多跨简支梁桥耦合振动分析

周 宏

(中铁十一局集团第一工程有限公司， 湖北 襄阳 441199)

中低速磁悬浮列车发展迅速，韩国、中国的中低速磁悬浮列车分别于2015年、2016年相继通车运行，国内还有多条磁悬浮快线仍在规划建设中。相对于地铁、高铁其他轨道交通，磁悬浮列车具有低噪声、低成本、低振动，绿色环保，转弯半径小，爬坡能力强等优点。为了节约土地和减轻地基沉降影响，中低速磁悬浮线路主要采用连续高架简支梁桥，其在总造价中所占比例60%～80%[1]。因此，研究中低速磁悬浮车桥耦合振动对行车质量、舒适性、经济效益以及未来磁悬浮列车的发展都意义重大。

国内外对于磁悬浮列车桥耦合振动做了大量研究：Cai等[2～4]研究了弹簧和阻尼代替电磁力的多刚体车桥振动模型，这样没有考虑控制电磁力的影响，不能充分体现磁悬浮车桥耦合振动特点。梁鑫等[5～7]对单跨简支梁桥下的磁悬浮车桥振动进行了分析，列车的振动响应难以达到稳定状况，不能反映实际情况中普遍存在多跨简支梁。武建军等[8,9]探讨了轨道平顺下的磁悬浮车桥振动。以上这些研究中桥梁计算基本上采用阵型叠加法，阵型为解析式，只能适用于等截面的简支梁桥和跨数较少的连续梁桥。为此，本文以通用有限元分析为基础，详细考虑磁悬浮列车、多跨简支梁桥、轨道不平顺和电磁力组成的大系统，主要对中低速磁浮列车-多跨简支梁桥的耦合振动进行精细化仿真分析。

1 磁浮列车-简支梁桥系统模型及动力方程

目前研究的磁浮列车主要分为EMS(Electromagnetic Suspension)型磁浮列车和EDS(Electrodynamic Suspension)型磁浮列车两种类型，其中EMS型磁浮列车依靠固定在悬浮架上的电磁铁与轨道上永磁体之间产生吸力而悬浮车体，而EDS型磁浮列车依靠车体上超导电磁力与轨道上的线圈之间产生斥力悬浮车体。EMS型磁浮列车又分为中低速磁浮列车和和高速磁浮列车。中低速磁浮列车UTM-01包含一个车体和三个悬浮架，高速磁浮列车TR06一般含有一个车体和四个转向架。本文以中低速EMS型磁浮列车UTM-01为研究对象。车体与悬浮架通过线性弹簧与阻尼连接，悬浮架通过控制电磁力与桥梁轨道相互作用。以单节中低速磁浮列车为例，单个悬浮架与桥梁之间电磁力采用4个集中力模拟，这正好满足精度要求，也就是悬浮架与轨道之间至少采用4个集中力来模拟均布电磁力[10]。如图1(图中：mc和mb分别为车体质量和转向架质量；yc和θc分别为车体的竖向位移和转动惯量；ybj和θbj分别为第j个转向架的竖向位移和转动惯量(j=1,2,3)；ks和cs分别为悬挂系统的刚度和阻尼；c0为中间弹簧阻尼系统到车体重心的横向距离；r0为弹簧阻尼系统到转向架重心的横向距离；ΔFi为第i(i=1,2,3,…,12)个波动电磁力)所示。中低速磁悬浮列车和高速磁悬浮列车参数如表1。

图1 中低速EMS型磁悬浮列车简化模型

1.1 电磁力方程

悬浮架与桥梁之间电磁力与电流和气隙之间的关系式是非线性的，对非线性电磁力平衡点附近进行泰勒展开，忽略高阶电流和气隙作用，则非线性电磁力可表示为[12,13]：

(1)

Fi=F0+ΔFi

(2)

(3)

(4)

电压、电流之间的关系式可表示为[14]：

(5)

式中：A为间隙处电磁铁铁芯的横截面面积；N为电磁铁线圈的匝数；μ为真空磁导率；R为线圈电阻；h0为额定气隙；i0为初始电流；ii为控制电流；M为悬浮体的总体质量(2442 kg)；Fi为第i个电磁力为平衡点处的电磁力(23.93 kN)；F0为平衡点处的电磁力(23.93 kN)；Δii为动态输出的电流；hi为第i个电磁力所对应的悬浮架与桥梁之间的气隙；Δhi为第i个电磁力所对应的悬浮架与桥梁之间气隙变化量；ΔUi为第i个控制反馈电压；g为重力加速度。

控制电压ΔUi采用悬浮架加速度、悬浮架速度和气隙间的相对变化位移Δhi反馈，即[15]：

(6)

Δhi=yei-ydi-ui

(7)

悬浮列车控制参数如表1所示[7,12,16]。悬浮

架和桥梁的位移，以及悬浮架的速度和加速度是依靠车体上的传感器进行测量，另外线性反馈控制能够促使气隙围绕在额定气隙上下波动。

1.2 磁悬浮列车动力方程

分别考虑车体、三个悬浮架的沉浮和点头共8个自由度yc，θc，yb1，θb1，yb2，θb2，yb3，θb3，如图1所示。单节磁悬浮列车的动力方程为：

(8)

(8i-16)c0ybi-2b0c0θbi]=0

(9)

i=1,2,3

(10)

3r0ΔF4i，i=1,2,3

(11)

1.3 简支梁桥动力方程

磁悬浮轨道的刚度远小于桥梁的刚度，故可忽略轨道对磁悬浮车体和桥梁之间耦合振动的影响[3]。简支梁桥动力方程采用有限元方法建立，完全具有通用性，能计算复杂的变截面简支梁桥、多跨连续梁桥和拱桥等，致使磁悬浮车桥振动分析能适应不同类型的桥梁。简支梁桥的动力方程为：

(12)

式中：Fv为电磁力Fi通过形函数转化的节点力列向量；Mv，Cv，Kv分别为桥梁的质量矩阵、阻尼矩阵和刚度矩阵，阻尼矩阵Cv采用刚度矩阵和质量矩阵Mv生成Rayleigh阻尼；yv为桥梁节点位移列向量。

简支梁桥参数如表2[3]。

表2 简支梁桥梁参数

1.4 轨道不平顺

磁浮轨道不平顺数值模拟的功率谱密度函数采用美国线路高低不平顺功率谱，其数学表达式为[10]：

(13)

式中：S(Ω)为轨道不平顺功率谱密度；Ωc为截断频率，取值为0.8245 rad/m；kp为安全系数，取常见值0.25；Av为粗糙度常数，取值为1.5×10-7m2/(rad/m)[7,11]。

车桥梁耦合振动中，整体坐标原点在多跨简支梁的最左端，磁悬浮列车和轨道不平顺的起始点距桥头20 m处。轨道不平顺采用三角函数进行模拟，选取的频率范围为0.1～1 rad/m，详细的模拟过程参考文献[17]，则轨道不平顺如图2所示。

图2 数值模拟轨道不平顺曲线

2 磁悬浮车桥耦合计算程序

基于自编的磁悬浮耦合计算程序，计算框架主要分为磁悬浮列车、桥梁(含轨道不平顺)和反馈控制力三大块，其中列车和桥梁通过反馈控制电磁力产生联系(图3)。磁悬浮列车和桥梁动力参数是先计算好的整体刚度矩阵、质量矩阵和阻尼矩阵，这样使程序具有通用性，能方便计算不同类型的列车和桥梁。在列车、桥梁和电磁力这三者动力计算循环过程中，当前时刻电磁力作用点对应的车辆悬浮架位移、速度和加速度及桥梁位移和速度通过反馈控制电压形成控制电流，控制电流和气隙计算出动态电磁力，动态电磁力同时作用在桥梁和列车上各自进行动力计算，同时桥梁上的动态电磁力还需叠加静态电磁力。磁悬浮列车上桥前，列车在轨道不平顺激励下振动，桥梁处于静平衡位置；悬浮列车上桥后，列车的动力响应受桥梁和轨道不平顺影响，列车和桥梁由于电磁力产生耦合振动；悬浮列车出桥后，桥梁自由振动，列车恢复到轨道不平顺激励下的振动直至计算时间结束。

3 计算程序正确性验证

采用德国TR06系列高速磁悬浮列车参数对程序的正确性进行验证，考虑一个车体四个转向架共10个自由度，参数取值如表1，2。TR06虽然属于高速磁浮列车，但仍然是EMS型磁浮列车，其竖向运动的数值模拟与中低速磁浮列车相同，故这里可以采用高速磁浮列车对程序的正确性进行验证。高速磁悬浮列车TR06以速度400 km/h通过多跨长度为24.768 m的简支梁桥，不同工况下车体振动稳定后的加速度曲线如图4所示，第1跨简支梁桥跨中位移随时间的变化曲线如图5。弹簧和阻尼替代电磁力的车桥耦合振动计算结果与文献[3]相同，说明程序在此工况中对于计算磁悬浮列车/桥梁耦合振动的正确性。当选取不同反馈控制参数，车体和桥梁振动响应结果能与弹簧阻尼代替电磁力的车桥耦合振动结果相近。因此，反馈控制方法和合适的控制参数能较好实现列车的悬浮。

图4 车体振动稳定后的加速度随时间变化曲线

图5 桥梁跨中位移随时间变化曲线

4 中低速磁悬浮列车-多跨简支梁梁桥耦合振动仿真分析

4.1 中低速磁悬浮列车-桥梁耦合振动响应

中低速磁悬浮列车计算参数参考韩国的UTM-01[12]，参数见表1。三节磁悬浮列车并列在距离桥头20 m处以100 km/h匀速驶向10跨长度为24.768 m的简支梁桥，未加轨道不平顺下车体的竖向振动随简支梁桥数量的变化情况如图6所示，第二节悬浮列车悬浮架与桥梁之间的平均气隙随桥梁数的变化情况如图7所示。车体在反馈控制下达到第4座桥时趋于稳定，上下做简谐振动，前后两车体的振动平衡点基本一致且小于中间车体。三节车先后上桥，各节车体引起桥梁竖向位移叠加，中间车体对应的桥梁位移大于前后两节车体，导致中间车体竖向振动平衡点跟着下降。车体简谐振动的平衡点随着桥梁的竖向位移往下移动，对桥梁的动力响应具有很好的跟随性。悬浮架与桥梁之间的气隙围着额定气隙10 mm上下波动，波动的幅值小于1 mm，反馈控制参数对于气隙有比较好的控制。

图6 车体位移随桥梁数的变化曲线

图7 气隙随桥梁数的变化曲线

4.2 轨道不平顺对耦合振动的影响

三节磁悬浮列车并列在距离桥头20 m处以100 km/h匀速驶向10跨长度为24.768 m的简支梁桥，轨道平顺与轨道不平顺下第一节车体的动力响应情况如图8所示。时程曲线中磁悬浮列车竖向振动具有随机性，由耦合振动过程中桥梁振动的确定性和轨道不平顺的随机性共同决定，微小的不平顺变化也能在车体的振动中反应出来，轨道线路设计施工中应严格减小轨道高低不平顺。图8时频转换后的振幅与频率的关系曲线如图9，可知从一个主频1.2 Hz变成两个主频1.2，0.42 Hz，其振幅也相应变大。因此，低频对车体的竖向振动影响较大，高频部分几乎对车体没有影响。

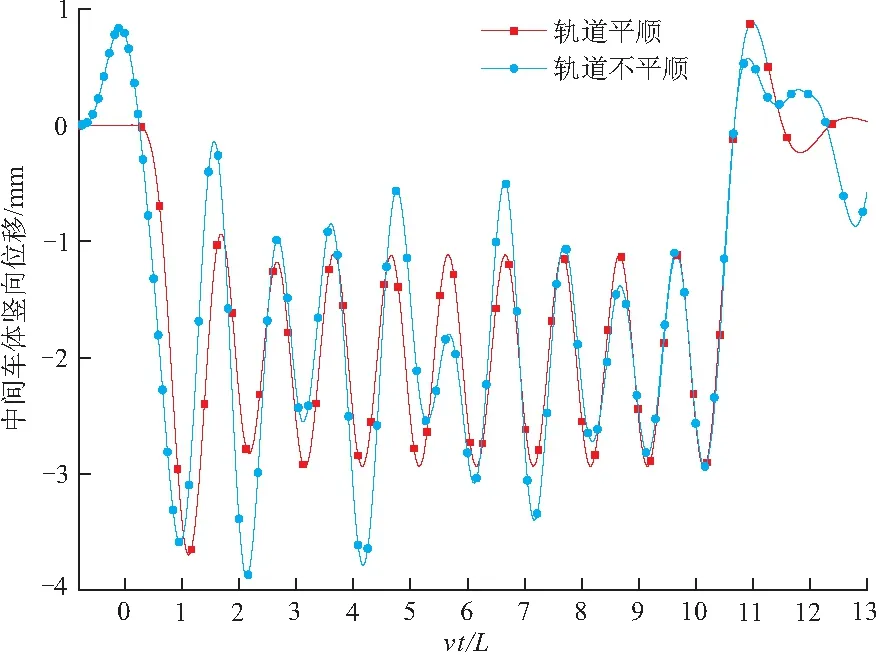
图8 车体竖向振动随桥梁数的变化曲线

图9 车体振幅随频率的变化曲线

简支梁桥由于自身刚度较大，轨道不平顺虽然对车体的振动影响大，但在列车中低速度下仍难以促使桥梁振动产生明显变化(图10)。轨道平顺与轨道不平顺的桥梁振动响应曲线基本一致。

图10 桥梁跨中位移随列车行驶距离的变化曲线

4.3 速度对车桥耦合振动的影响

不考虑轨道不平顺的影响，主要分析磁悬浮列车在中低速下车桥耦合振动稳定后各振幅的变化。图11中车体简谐振动的振幅随着速度的增大先增大后减小，前后车体振幅始终比较接近且明显大于中间车体的振幅。中低速度下车速为56.7 km/h时车体的竖向振动达到最大，磁悬浮列车在24.768 m简支梁桥行驶过程中应尽量远离此速度。悬浮架与桥梁之间的平均气隙幅值随速度变化曲线如图12所示，气隙随着速度的增大而增大，悬浮架5与桥梁之间的平均气隙在速度为20 km/h下的0.18 mm迅速增加到速度为100 km/h下的0.8 mm，磁悬浮列车速度对气隙影响较大。

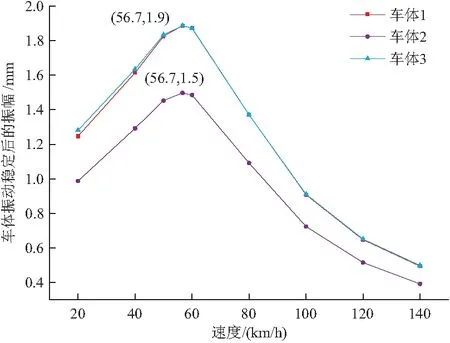
图11 车体振动稳定后的振幅随车速的变化曲线

图12 气隙振幅随车速的变化曲线

不同速度下的第一座简支梁桥跨中位移曲线如图13所示，其中桥梁跨中位移变化不大，中低速对车桥耦合振动的桥梁影响较小。

图13 桥梁跨中位移随距离的变化曲线

5 结 论

(1)本文基于自编程序，建立通用的中低速磁浮列车-桥梁耦合确定性振动分析平台，能方便实现不同系列车体和不同桥梁的精细化分析，并对程序的正确性进行了验证。

(2)磁悬浮车桥耦合振动过程中，车体振动的平衡位置会随着桥梁发生的竖向位移向下移动，且前后车体简谐振动振幅大于中间车体；

(3)轨道不平顺主要对车体的振动响应产生影响，而对桥梁的振动影响较小，而轨道不平顺中主要是低频部分对车体动力响应影响大，应严格控制磁悬浮线路轨道不平顺的低频部分以提高乘客的舒适性；

(4)中低速磁浮列车行驶速度对气隙和车体振动影响较大，而对桥梁的振动影响小，车体的振幅随着车速增大先增大后减小，在车速为56.7 km/h时最大。