软黏土中坑中坑式抗隆起稳定安全系数计算

李惠霞， 何鑫龙， 繆广吉， 周宏伟， 林上顺

(1. 福建工程学院 土木工程学院， 福建 福州 350118； 2. 中铁二局第三工程有限公司， 四川 成都 610041； 3. 福州大学 土木工程学院， 福建 福州 350116)

沿海地区的土体含水率高、强度低、变形量大，在软土地区的基坑开挖过程中，坑底隆起破坏是最常见的一种破坏形式。在进行软土地区基坑设计的过程中，对基坑的抗隆起稳定性进行验算十分关键。坑中坑在软土地区基坑工程中大量存在[1,2]，坑中坑在基坑的底部进行二次开挖，破坏原有的应力平衡，使应力重新分布，导致基坑的抗隆起稳定性发生明显下降。目前关于基坑抗隆起稳定性研究的方法中鲜有考虑坑中坑的影响，需要对其进一步改进，以适用于坑中坑式基坑的抗隆起稳定性分析。

基坑抗隆起稳定的计算方法主要有传统的极限平衡法和极限分析法，以及数值分析法。极限平衡法中基于地基承载破坏理论的方法中最经典的是Terzaghi[3,4]提出的公式，分别适用于浅基坑和深基坑的抗隆起稳定性计算，其计算简单、方便，但是不能考虑大量因素对抗隆起稳定性的影响，因此许多学者通过改进提出了不同的公式。极限平衡法由于原理简明，在实际工程中常被采用，但需要事先假定破坏面。而假定的破坏面与实际情况不同，导致计算结果与真实值存在差距。极限分析法以塑性力学的理论为依据，通过假定运动许可的速度场和静力许可的应力场，根据功能相等原理，得到基坑抗隆起稳定安全系数的上下限，使其结果更为可靠。如Chang等[5]提出的Prandtl滑移破坏模式的极限分析法和秦会来等[6]提出的多块体相容破坏机构的上限分析法。极限分析法计算过程中仍然需要进行大量的人为假定，其适用范围依然存在许多限制。结合有限元能够处理复杂荷载和边界条件的优点，Ukritchon等[7]采用极限有限元法分析基坑隆起稳定性，能够得到可靠的基坑抗隆起稳定安全系数上下限解。弹塑性有限元法中强度折减有限元法分析基坑的抗隆起稳定性是一种主要的方法。Goh等[8,9]用该方法来分析软黏土中基坑分别在二维和三维条件下的抗隆起稳定性。Do等[10]发现在强度折减有限元分析中采用交点法得到的基坑抗隆起稳定安全系数更精确。许多学者针对不同的工况和基坑形式展开了大量的分析[11～13]。

国内大量规范采用极限平衡法中的另一种圆弧滑动法进行抗隆起稳定性分析。传统的圆弧滑动法计算基坑抗隆起稳定安全系数存在两种破坏面的假定形式，其中一种假定圆弧的圆心位于挡墙与最后一道支撑的交点处，另一种是将圆心假定位于坑底与挡墙的交点处，如图 1中的圆弧A1B1C1E1和A2B2C2E2所示，通过构建力矩平衡确定基坑的抗隆起稳定性。姜洪伟等[14,15]发现采用前一种计算得到的抗隆起稳定安全系数更合理。许多学者对传统的圆弧滑动法进行了改进，一方面考虑软土的非均匀性与土体强度的各向异性，Hsieh等[16]用圆弧滑动法分析不同试验得到的土体不排水抗剪强度对抗隆起稳定性计算结果的影响，发现采用三轴不排水不固结试验得到的强度进行计算最为合理。郑刚和程雪松[17]通过弧长和法向应力加权平均的方法，考虑分层土地基中土层分布对抗隆起稳定性的影响。应宏伟等[18]采用试验得到的土体强度各向异性不排水强度公式推导圆弧滑动法的计算公式。另一方面改变圆弧滑动面的选取方式，王洪新[19]对圆弧滑动法进行改进，通过移动圆弧的圆心使其适用于狭窄基坑的抗隆起稳定安全系数的计算。应宏伟等[20]通过数值模拟确定滑裂面的分布规律，进而假定圆弧滑动法的滑动面，并修正了狭窄基坑被动侧的被动土压力系数，提出了狭窄基坑的圆弧滑动法计算公式。可以发现，在圆弧滑动法计算过程中不同的圆弧滑动面选定对计算结果有较大的影响，根据基坑的不同情况需要事先确定较为合适的滑动面。

图1 传统圆弧滑动法

考虑到坑中坑的存在会对原基坑的破坏模式产生影响，对传统的圆弧滑动法进行改进，通过移动圆弧圆心的方法使其适用于坑中坑式基坑抗隆起稳定安全系数的计算，再通过搜索得到最危险破坏面的抗隆起稳定安全系数。并与强度折减有限元分析计算的抗隆起稳定安全系数进行对比验证。

1 圆弧滑动法的改进

采用极限有限元软件OptumG2 (Academic Version)建立坑中坑式基坑的二维有限元模型。土体简化为黏土层与砂土层，用HMC(Hamiltonian Monte Carlo)模型进行模拟，考虑基坑周围土体多为饱和黏土，且只考虑短期工况，土体假定为不排水条件，黏土层土体强度取不排水参数，砂土层取排水参数，土层的具体物理力学参数指标如表1。内外坑的挡墙均采用板单元进行模拟，外坑设两道内支撑用连接件进行模拟。基坑围护结构的各项物理力学参数指标如表2 所示。内外坑围护墙与土体接触面的强度折减系数为Rinter=0.8。考虑到坑中坑式基坑的破坏模式和抗隆起稳定安全系数与外坑宽度B、外坑深度H、内坑宽度b、内坑深度h、内外坑之间的平台宽度W、外坑挡墙插入深度D、内坑挡墙插入深度d、软土层不排水抗剪强度Su等参数有关。建立多组模型，各组模型的具体参数取值如表3。土体在不同应力路径下的变形和破坏特征是不同的，先采用弹塑性分析对基坑的开挖进行模拟：(1)计算初始应力；(2)设置外坑围护结构；(3)降低坑内水位至第一层开挖面下0.5 m；(4)开挖第一层土体；(5)设置第一道内支撑；(6)重复以上步骤至外坑坑底；(7)设置内坑围护结构；(8)开挖至内坑坑底。在弹塑性分析后再采用强度折减法分析坑中坑式基坑的破坏模式。

表1 有限元中土体物理力学参数

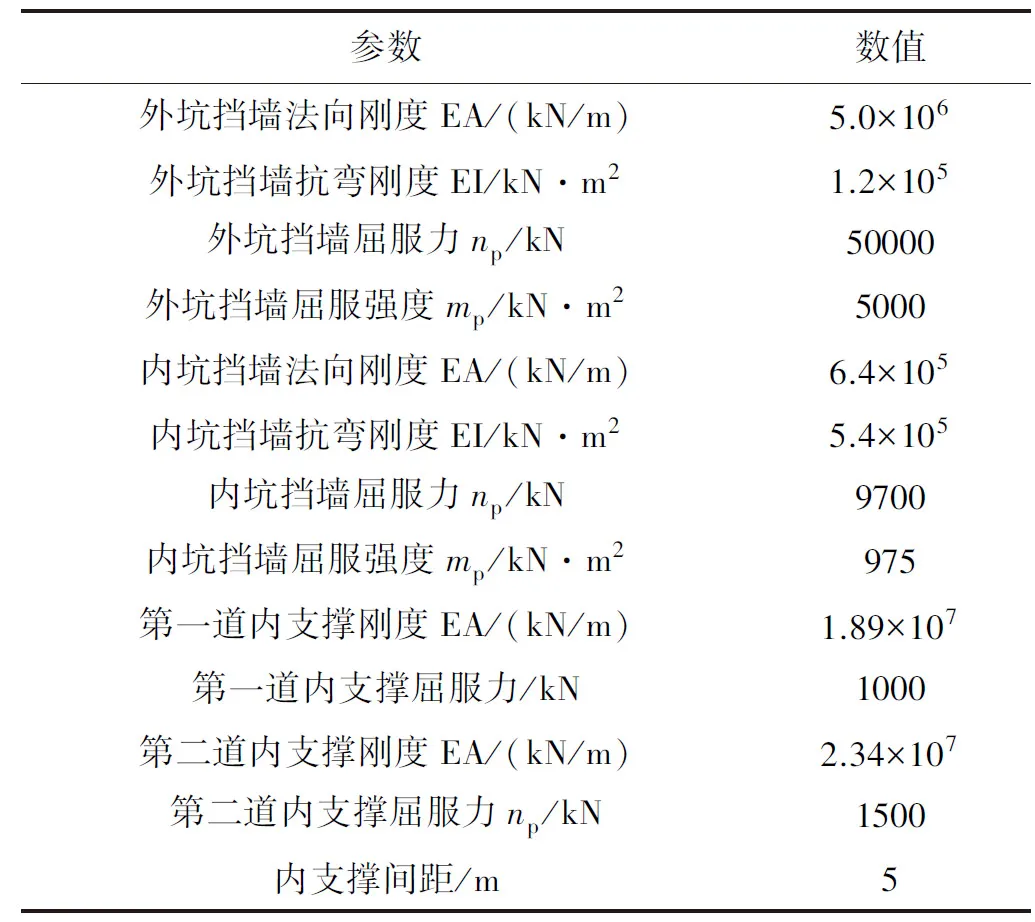
表2 支护结构物理力学参数

表3 有限元分析中各参数取值

对强度折减有限元分析得到的破坏模式进行总结，存在三种破坏模式：内外坑整体隆起破坏(M1)，内外坑整体破坏面和外坑独立破坏面同时存在(M2)，外坑独立破坏(M3)，如图2所示。Sun等[2]对传统的圆弧滑动法进行改进，取内外坑间平台的中间位置为圆弧的圆心，在破坏模式为内外坑整体隆起破坏时(M1)，建立圆弧滑动法假定的滑动面，从而推导坑中坑式基坑的抗隆起稳定安全系数的计算公式。但是通过有限元分析得到的破坏面可以发现，滑动面的圆心并不一定位于内外坑间平台的中间位置。Sun等[2]的方法只考虑了均质土体，采用c-φ土体强度指标进行抗隆起稳定安全系数公式的推导，且只能应用于破坏模式为内外坑整体破坏面时的抗隆起稳定安全系数的计算，无法考虑破坏模式为内外坑整体破坏面和外坑独立破坏面同时存在以及外坑独立破坏面的情况。

图2 坑中坑式基坑的抗隆起破坏模式

考虑软黏土地区基坑开挖过程中，短期的不排水抗剪强度起控制作用，取不排水抗剪强度指标进行分析，采用十字板原状土试验得到的不排水强度指标Su，由于土体的非均质性，近似取黏土不排水抗剪强度随深度线性增大。

Su=n+mZ

(1)

式中：n为地表的不排水抗剪强度；Z为距地表以下的深度。在此基础上构建内外坑整体圆弧滑动面和外坑独立圆弧滑动面的力矩平衡，再通过搜索确定安全系数最小的圆弧滑动面，得到坑中坑式基坑的抗隆起稳定安全系数。

1.1 圆弧滑动面构建

根据有限元的计算结果可以发现内外坑整体破坏面交于内坑底面，通过外坑挡墙底部，并与地表相交。内外坑整体圆弧滑动面的计算公式为：

(2)

式中：x1，y1分别为圆弧圆心的横纵坐标；R1为圆弧的半径。为了计算整体圆弧滑动面的稳定安全系数，对圆弧滑动面构建力矩平衡，如图3所示，产生滑动力矩的项为ABGF区域的土体自重；产生抗滑力矩的项包括滑裂面ABC的抗滑力矩和IJCE区域内抗滑力矩的损失，以及外坑挡墙提供的抗滑力矩。

图3 内外坑整体圆弧滑动面计算模式

(1)滑裂面ABC上的抗滑力矩Mr为：

(3)

(2)IJCE区域开挖引起抗滑力矩的损失ΔM为：

(4)

(3)ABGF区域引起的滑动力矩Ms为：

(5)

针对坑中坑式基坑的内外坑整体圆弧滑动面，抗隆起稳定安全系数FS1的计算公式定义为抗滑力矩和滑动力矩的比值：

(6)

式中：Mk为外坑挡墙所提供的抗滑力矩。

当破坏模式为内外坑整体破坏面和外坑独立破坏面同时存在(M2)与外坑独立破坏面(M3)时，通过有限元计算结果可发现，外坑的独立破坏面通过外坑挡墙的墙脚点，与内外坑间的平台相交，此时外坑独立破坏面的圆弧模式接近普通基坑的圆弧滑动面的模式。不同的外坑独立圆弧滑动面的公式为：

(7)

式中：y2为外坑独立圆弧滑动面圆心的纵坐标；R2为外坑独立圆弧滑动面的半径。为计算外坑独立圆弧滑动面的稳定安全系数，对圆弧滑动面构建力矩平衡，如图4所示，产生滑动力矩的项为ABOF和BCGO区域的土体自重；产生抗滑力矩的项包括滑裂面ABCE的抗滑力矩，及外坑挡墙提供的抗滑力矩。

图4 外坑圆弧滑动面计算模式

(1)滑裂面AB上的抗滑力矩Mr1为：

(8)

(2)滑裂面BCE上的抗滑力矩Mr2为：

(9)

(3)ABOF区域引起的滑动力矩Ms1为：

(10)

(4)BCGO区域引起的滑动力矩Ms2为：

(11)

外坑独立圆弧滑动面的抗隆起稳定安全系数FS2定义为抗滑力矩Mr和滑动力矩Ms的比值：

(12)

1.2 最危险滑动面搜索

内外坑整体破坏面交于内坑底面，通过外坑挡墙底部，并与地表相交。因此选定地表点ai为圆弧滑动面的顶端，选定内坑底面点ci为圆弧滑动面的底端，与外坑挡墙底部的点bi三点可以确定一个圆弧，进而得到圆弧圆心坐标和圆弧的半径，如图5所示。构建程序沿着方向1，2，3搜索由内坑底面、地表和外坑挡墙延长线上不同点构成的圆弧面，并把圆心坐标限制在x≥0的区域内，得到安全系数最小的最危险圆弧滑动面。取b/10为坐标步长分为三个步骤进行搜索，具体的搜索步骤为：(1)假定a1，b1为最危险破坏面上的点，通过搜索方向2上的点得到安全系数最小的破坏面a1b1ck；(2)取点a1，cj构建圆弧滑动面，通过搜索方向3得到安全系数最小的破坏面a1bjck。(3)取点bjck构建圆弧滑动面，通过搜索方向1得到安全系数最小的破坏面aibjck。

图5 最危险内外坑整体圆弧滑动面搜索

外坑的独立破坏面通过外坑挡墙的墙脚点，与内外坑间的平台相交，此时外坑独立破坏面的圆弧模式接近普通基坑的圆弧滑动面的模式。因此选定外坑挡墙上的Oi点为圆弧滑动面的圆心，使滑动面始终通过外坑挡墙的墙脚。根据圆心和外坑挡墙墙脚点，可以确定一个圆弧，并采用垂线从圆弧的底端bi延伸至地表点ci，如图6所示。全面搜索外坑挡墙上不同圆心点构成的滑动面，得到安全系数最小的最危险滑动面。具体的搜索步骤为：构建以外坑挡墙上的Oi为圆心，且通过外坑挡墙底部的圆弧滑动面，以b/10为坐标步长对外坑挡墙上的圆心进行搜索，便可得到安全系数最小的最危险滑动面。

图6 最危险外坑圆弧滑动面搜索

针对内外坑整体破坏面的破坏模式(M1)，选取搜索得到的最危险内外坑整体圆弧滑动面的安全系数FS1为该模式抗隆起稳定安全系数。内外坑整体破坏面和外坑独立破坏面同时存在的破坏模式(M2)，对比搜索得到的最危险外坑独立滑动面和最危险内外坑整体滑动面安全系数，选取较小值(min{FS1,FS2})为该破坏模式下的抗隆起稳定安全系数。当破坏模式为外坑独立破坏面的破坏模式(M3)时，选取搜索得到最危险外坑独立圆弧滑动面的安全系数FS2为该破坏模式的抗隆起稳定安全系数。

2 计算结果对比

采用极限有限元软件OptumG2[21]中的强度折减有限元分析和改进的圆弧滑动法进行对比，图7为对比强度折减有限元法和改进的圆弧滑动法计算得到的坑中坑式基坑抗隆起稳定安全系数

图7 改进圆弧滑动法和强度折减有限元法计算结果对比

在不同的内坑宽度和深度、平台宽度、土体不排水抗剪强度强度下的变化趋势。可以发现，改进的圆弧滑动法和上限有限元法得到的抗隆起稳定安全系数随内坑宽度和深度、平台宽度，土体强度增大的变化规律基本相近。采用改进的圆弧滑动法计算得到的抗隆起稳定安全系数能接近强度折减有限元计算得到的抗隆起稳定安全系数，但是圆弧滑动法的计算结果总体上还是略小于上限有限元的计算结果。有限元计算中能够得到一定条件下基坑的全部破坏范围和形态，而圆弧滑动法限定于假定的破坏面，两者的破坏形态不相吻合是导致抗隆起稳定安全系数计算存在差异的主要原因。

3 结 论

(1)对传统的圆弧滑动法进行改进，通过移动圆弧的圆心位置使圆弧滑动法适用于坑中坑式基坑抗隆起稳定性分析，再经过全面搜索得到最危险的滑动面，确定坑中坑的抗隆起稳定安全系数。

(2)对比改进的圆弧滑动法和强度折减有限元计算得到的抗隆起稳定安全系数，可以发现改进的圆弧滑动法计算得到的抗隆起稳定安全系数与强度折减有限元的计算结果能够较好地吻合。