基于改进相关向量机的滚动轴承剩余寿命预测方法

张 钢，谭 波，梁伟阁，田福庆

(海军工程大学兵器工程学院,湖北 武汉 430033)

0 引言

滚动轴承是各类旋转机械中最常用的通用零部件之一，也是旋转机械易损件之一。滚动轴承一旦发生故障，将导致灾难性事故。因此，预测滚动轴承剩余寿命具有重要意义[1]。

智能预测技术是滚动轴承剩余寿命预测的主要手段之一，其中相关向量机(relevance vector machine, RVM)具有较好的稀疏性、泛化能力，逐渐成为剩余寿命预测领域的研究热点。文献[2]针对风电功率序列非线性、非平稳性等特点，提出一种基于混沌布谷鸟搜索算法优化相关向量机的短期风电功率预测方法。文献[3]提出一种基于相关向量机的电力负荷中期预测方法。RVM虽然具有较高的中短期预测精度，但是由于机械部件性能退化复杂性，导致RVM预测算法出现长期趋势预测精度不高的问题[4]。同时，相关向量机模型在预测过程中包括数据重构和迭代预测两个过程，计算效率较低[5-7]。本文针对此问题，提出了基于改进相关向量机的滚动轴承剩余寿命预测方法。

1 改进相关向量机原理

1.1 相关向量机原理

ti=y(xi)+ε

(1)

式(1)中，N是样本数，y(xi)表示非线性函数，ε是独立同分布的高斯噪声，且ε～N(0,σ2)。

非线性函数y(x)可以表示为核函数乘以相应权重系数后的求和：

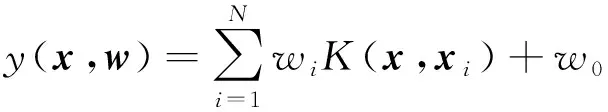
(2)

式(2)中，w=[w1,w2,…,wN]T是权重向量，wi表示第i个训练数据对应的权值，w0表示偏置参数，K(x,xi)是核函数。因此，目标输出值ti∈R的概率分布是均值为y(x,w)，方差为σ2的高斯分布。在整个训练数据集上的似然函数可以表示为：

(3)

式(3)中，t=[t1,t2,…,tN]T；ω为全部权重系数和偏置组成的向量，ω=[w0,w1,…,wN]T；Φ=[φ1,φ2,…,φN]T表示输入向量带入核函数后得到的N×(N+1)维矩阵，φi=[1,K(xi,x1),…,K(xi,xN)]，i=1,2,…,N。

假设ωi概率分布为0附近的高斯分布，即满足：

(4)

式(4)中，αi为权重ωi对应的超参数，决定权重的分布范围。各权重相互独立，因此，对所有权重ω有：

(5)

式(5)中，α为由N+1个超参数αi组成的向量，α=[α0,α1,…,αN]T。

根据参数的先验分布，结合贝叶斯推理可知，所有未知参数的后验分布可以表示为：

(6)

因此，根据新的输入样本x*，预测输出值t的概率分布为：

(7)

式(7)的近似解为：

(8)

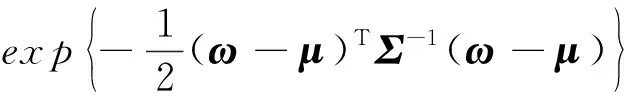
(9)

式(9)中，C=σ2I+ΦA-1ΦT，μ和Σ是权重后验分布的均值和方差：

μ=σ2ΣΦTt

(10)

Σ=(A+σ-2ΦTΦ)-1

(11)

式(10)中，A=diag(α0,α1,…,αN)。

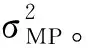
(12)

(13)

式(12)、式(13)中，γi=1-αiΣii，γi∈[0,1]，Σii表示权重方差矩阵的对角线元素。

当给定新的输入样本x*，输出值t*的概率分布为：

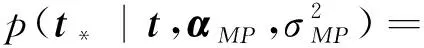
(14)

由式(8)和式(9)可知，式(14)积分项的两部分都是高斯函数乘积形式，因此积分后的结果为：

(15)

其中，

y*=μTΦ(x*)

(16)

(17)

由式(16)、式(17)可知，相关向量机不仅能够给出预测值的期望，同时能够给定预测值的置信区间。

1.2 改进相关向量机模型

相关向量机虽然能够提供预测结果的置信区间，但是面对大量训练数据，存在计算效率低、长期预测能力较差、预测结果受核函数的影响较大等问题。本节提出一种结合多项式函数的改进相关向量机方法，并将其应用于滚动轴承剩余寿命预测中。

多项式回归模型具有较强的曲线拟合能力，长期预测精度较高，但是属于点估计方法，无法根据历史数据获得预测结果的置信区间。本节将多项式回归模型较强的长期预测能力与相关向量机相结合，提出一种改进相关向量机的剩余寿命预测模型。

多项式回归模型的数学表达式为：

y=a0+a1x+a2x2+…+anxn

(18)

式(18)中，y是目标函数值，x是输入值，a0,a1,a2,…,an是模型系数。

2 基于改进相关向量机的剩余寿命预测方法

基于改进相关向量机的剩余寿命预测算法流程如下：

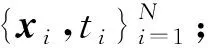
输出：预测值y*和预测值的置信区间；

步骤2 初始化参数{αi}和σ2；

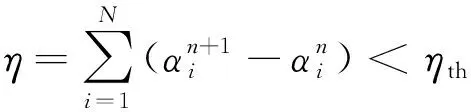
步骤4 根据式(12)和式(13)更新αi和σ2；

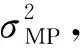
步骤6 利用相关向量xRV确定多项式回归模型系数，计算各训练样本输入值xi到多项式曲线的距离；

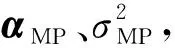
步骤8 给定预测数据x*，代入式(18)，计算得到预测值y*，利用式(17)计算得到预测值的置信区间。

3 试验与分析

3.1 试验介绍

XJTU-SY滚动轴承试验数据是由西安交通大学设计科学与基础构件研究所和长兴昇阳科技有限公司合作试验采集得到[8]。

XJTU-SY滚动轴承试验平台由一台交流感应电机、一台电机转速控制器、一个支撑轴、两个支撑轴承(重型滚动轴承)和一个液压加载系统组成，如图1所示。该试验平台旨在开展滚动轴承在不同工况下(如不同径向力和转速)的加速退化试验。液压加载系统产生径向力并施加于被测轴承壳体上，交流感应电机的转速控制器可以控制滚动轴承转速。为了采集被测轴承的振动信号，在被测轴承壳体上放置两个PCB 352C33型加速度计，一个安装在水平轴承，另一个安装在垂直轴上。加速度计的采样频率设置为25.6 kHz，采样时间为1.28 s，采样周期为1 min。

图1 XJTU-SY滚动轴承试验平台Fig.1 XJTU-SY bearing experimental platform

试验所用轴承型号为LDK UER204轴承，共有三种运行工况，每类工况下做五组试验。各工况条件如表1所示。

表1 试验工况

由于负荷加载在水平方向，水平方向的传感器能采集到更多的运行状态信息。因此，采用水平方向的振动加速度信号开展剩余寿命预测研究。水平方向的原始振动加速度信号如图2所示。

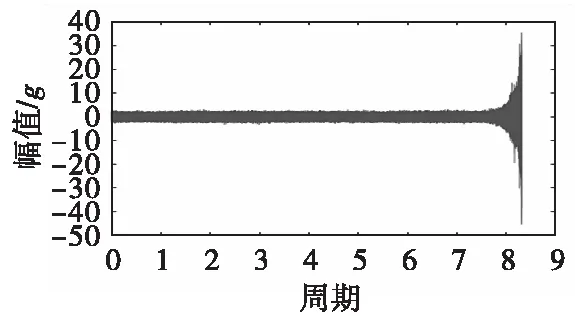
图2 水平方向的原始振动加速度信号Fig.2 The original vibration acceleration signal of horizontal direction

由图2可知，在正常运行工况下，振动加速度信号仅有小范围的波动，因此很难利用这类历史数据预测剩余寿命。当滚动轴承进入性能退化阶段时，振动加速度值随着运行时间的增加而不断增加，其包含丰富的性能退化信息，因此选用这一阶段的振动加速度信号作为历史监测数据预测剩余寿命。预测起始点的选择采用文献[9]介绍的自适应性能退化检测方法。当滚动轴承的振动加速度幅值超过20g时，将存在严重的安全问题，本文将振动加速度为20g时的滚动轴承定义为失效轴承。

3.2 剩余寿命预测

确定滚动轴承起始预测时间点Ts后，利用训练好的改进向量机模型性能退化曲线，当性能退化曲线达到失效阈值(20g)时，对应的时间即为失效时刻Tfail_pred。当前时刻到预测失效时刻的差值即为滚动轴承剩余寿命，根据文献[10]，滚动轴承剩余寿命定义为：

RUL(Ts)=inf{t:f(t+Ts)≥η|f}

(19)

式(9)中，RUL(Ts)是自预测起始时刻Ts的剩余寿命，f(t+Ts)是t+Ts时刻预测的性能退化状态，f所有的健康因子，η是失效阈值。

本文提取最大幅值(maximum amplitude, MA)作为滚动轴承健康因子，得到不同工况下比较典型的全寿命周期健康因子曲线如图3所示。

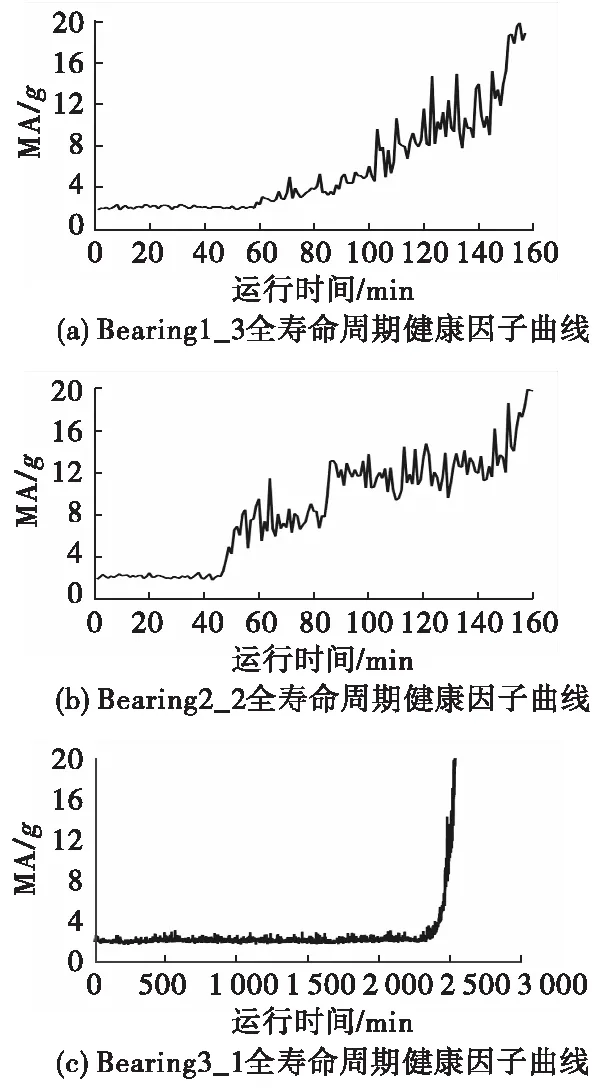
图3 不同工况下典型的全寿命周期健康因子曲线Fig.3 Typical life cycle health factor curves under different working conditions

以工况3下bearing3_1为例，利用本文提出的基于改进相关向量机的剩余寿命预测方法得到性能退化曲线如图4所示。

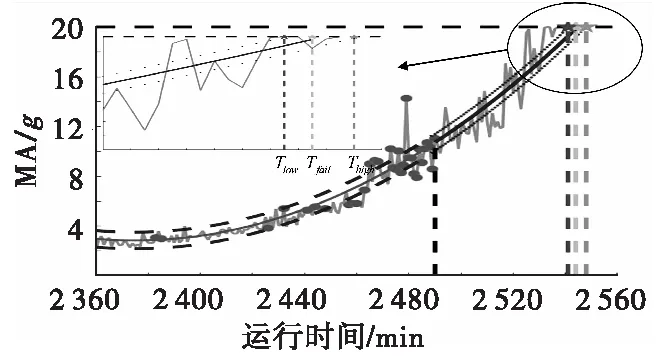
图4 Bearing3_1的性能退化预测曲线Fig.4 The predicted degradation curve of Bearing3_1

图4中，折线表示健康因子曲线，圆点表示相关向量，通过折线和圆点的光滑曲线表示多项式回归模型拟合曲线，最左侧的竖直点划线后的光滑曲线表示性能退化预测曲线，两条点线之间表示预测值的置信区间。竖直方向，由左至右，依次表示预测起始时刻，预测失效时刻，预测失效时刻的上置信区间点，预测失效时刻下置信区间点。

预测起始时刻为Ts=2 430 min，预测轴承失效时刻为Tfail_pred=2 535 min，实际的失效时刻为Tfail_real=2 537 min。因此，带入剩余寿命计算公式(19)，预测的剩余寿命为RULpred=105 min，实际剩余寿命为RULreal=107 min，剩余寿命预测结果的置信区间为[103,108]min。由图4和以上数据可以看出，本文提出的方法能够有效预测滚动轴承剩余寿命，实际剩余寿命包含在置信区间中，预测的剩余寿命小于实际剩余寿命，在工业应用中，有利于提前预警。

3.3 对比分析

为了进一步说明本文所提方法的有效性，分别利用原始相关向量机、深度置信网络和粒子滤波方法预测滚动轴承剩余寿命。以bearing3_1为例，起始预测点为Ts=2 430 min，各类方法得到的剩余寿命预测结果如图5所示。

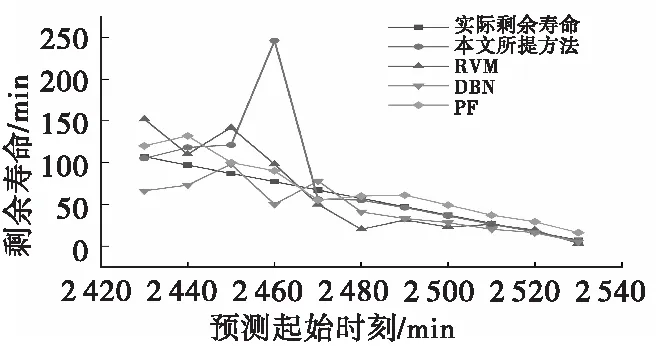
图5 不同方法得到的剩余寿命预测结果Fig.5 The remaining useful life prediction results of different methods

图5中，曲线分别表示实际剩余寿命，基于改进RVM预测的剩余寿命，基于RVM预测的剩余寿命[11]，基于深度置信网络(deep belief network, DBN)预测的剩余寿命[12]，基于粒子滤波(particle filtering, PF)算法得到的剩余寿命[13]。其中深度置信网络是一类目前较火的基于深度学习网络的剩余寿命预测模型，属于数据驱动的剩余寿命预测方法；粒子滤波属于典型的机理驱动的剩余寿命预测方法。

由图5可知，基于改进相关向量机的剩余寿命预测方法能够较快的收敛，且预测精度较其他三种预测方法有提高。相较于RVM，长期预测精度得到有效提高。相对于RVM和PF，基于DBN的剩余寿命预测方法预测精度提高，但是其预测结果属于点估计，无法提供预测置信区间。改进RVM在预测点Ts=2 460时，预测结果偏差较大，主要原因是当起始预测点为Ts=2 460时，由图4可知滚动轴承健康因子曲线突然变陡峭，从而预测得到的剩余寿命出现较大误差，但随着数据量的增加，采用改进相关向量机的剩余寿命预测结果迅速收敛于实际剩余寿命，说明该方法具有较好的鲁棒性。

在运算量方面，本文所提的改进方法主要包括两部分的计算内容：一是训练阶段；二是预测阶段。在训练阶段，利用相关向量机模型对训练数据稀疏化处理，得到相关向量，利用相关向量确定多项式回归模型参数，该阶段计算时间要长于单独训练相关向量机模型的时间。预测阶段，利用多项式回归模型直接预测性能退化趋势，省略数据重构及迭代预测过程，因此该阶段的计算时间比利用相关向量机模型进行预测的时间短。以文中bearing3_1训练、测试过程为例，总得计算时间为21.4 s，而单独使用相关向量机模型的计算时间为23 s。综上，本文所提方法的运算量比相关向量机模型运算量要小，提高了计算效率。

4 结论

本文提出了基于改进相关向量机的滚动轴承剩余寿命预测方法。该方法综合多项式回归模型长期趋势预测精度高，相关向量机能够提供稀疏的相关向量和提供预测结果置信区间的优势，有效提高了滚动轴承寿命预测精度，且所提方法在预测阶段不需要数据重构和迭代预测过程，提高了计算效率。试验结果表明，本文所提方法能够有效提高剩余寿命精度和计算效率，并提供预测置信区间，有利于制定维修计划。