改进的中心差分卡尔曼滤波水下被动目标跟踪

郑 艺，王明洲，胡友峰

(1.中国船舶集团有限公司 第 705 研究所，陕西 西安 710077；2.中国船舶集团有限公司 第705研究所昆明分部，云南 昆明 650118)

0 引 言

对水下目标进行识别和跟踪对于潜艇、鱼雷、水下无人潜航器等来说至关重要，是保证它们安全作业的重要环节。为了保证自身安全，不主动向外辐射能量的前提下，被动地对目标运动状态进行估计是很有必要的。而单站纯方位目标跟踪所需观测者少、隐蔽性强，应用场景广泛[1-2]。距离目标较近时由于方位抖动影响更大，使得滤波容易出现不稳定、甚至发散的情况。同时，这种情形下的一个难点是目标状态的潜在不完全可观测性，因此状态估计难度更大[3-4]。

单站纯方位目标跟踪是非线性问题，非线性滤波是解决这一问题常用的有效方法之一。扩展卡尔曼滤波（Extanded Kalman Filter，EKF）[5]是较早应用于目标跟踪的非线性滤波方法，但其仅为1阶近似，线性化误差较大，滤波的精度和稳定性较差[6]。采样型方法是实现非线性滤波的另一类方法，包括确定性采样和随机采样。以粒子滤波[7]（Particle Filter，PF）为代表的随机性采样计算量过大，且可能会出现粒子退化或贫乏的问题，在工程应用中具有局限性[8]。

确定性采样方法包括无迹卡尔曼滤波（Unscented Kalman Filter，UKF）[9]、容积卡尔曼滤波[10]（Cubature Kalman Filter，CKF）、中心差分卡尔曼滤波（Central Difference Kalman Filter，CDKF）[11-12]等。其中UKF 是应用最广泛的一种方法[13-14]，可达至少 2 阶近似，但需要根据运动或观测模型的非线性来选择α，β，λ三个参数，难以找到参数的最优值。在UKF基础上的平方根无迹卡尔曼滤波（Square Root Unscented Kalman Filter，SR-UKF）也是一种用途广泛的滤波方法，具有较好的稳定性，是一种经典的平方根类的方法，在水下目标跟踪中有较好的效果[15-16]。因此本文也将SR-UKF作为一种对比方法加入到仿真中。

CDKF也是确定性采样方法中的一种，它选取采样点的方式与UKF不同。CDKF基于Sterling 多项式插值公式，对非线性函数按中心差分形式逼近，可达至少2阶近似。CDKF精度与UKF相当，且只需调整1 个参数h。因此 CDKF 在目标跟踪[17-18]、导航系统[19]等方面都有较好应用。但单站纯方位目标跟踪系统的可观测性差、观测噪声影响大，致使滤波器不稳定[3-4]，尤其在目标距离近的情况下这种现象更常见。

本文目的是解决在近距离的纯方位观测情况中，单站纯方位目标跟踪中CDKF容易出现的滤波不稳定问题。因此提出了一种CDKF的改进方法，在采样点的协方差和量测协方差中采用QR分解计算协方差平方根，而在协方差平方根更新时使用更为稳定的奇异值分解（Singular Value Decomposition，SVD）进行计算，提高算法的稳定性和估计精度。

1 问题描述和滤波方法

1.1 单站纯方位目标跟踪

对于水下目标，在许多情况下，目标的运动是非机动的。因此，近似等速（Nearly Constant Velocity，NCV）模型[5,20]适用于水下被动目标跟踪场景。本文考虑二维平面运动模型，非机动目标和机动的观测站。

目标的运动状态可以表示为向量：

其中：xk，yk表示目标位置对应的坐标，表示目标的速度分量。对于NCV模型，目标匀速直线运动，系统的状态方程可表示为：

其中： Φ 为状态转移矩阵；w(k)为均值为0方差为Q的系统噪声：

系统的观测方程可表示如下：

其中：v(k)为均值为0方差为R的观测噪声。对于单站纯方位目标跟踪系统，观测函数为：

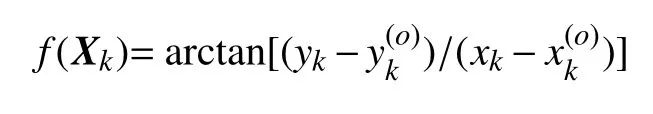
纯方位目标跟踪是典型的非线性滤波问题，式（1）和式（4）组成了系统状态空间模型。对于单站纯方位量测来说，观测站机动是系统完全可观测的必要条件而非充分条件，观测站的机动情况对滤波效果起着关键作用，但在近距离追击目标的情况下，观测站较大机动容易丢失目标，因此只能小机动或者不机动，因此系统可观测性受限。

1.2 中心差分卡尔曼滤波

假设系统状态变量是服从高斯分布的，且均值和协方差已知。CDKF的核心思想是利用斯特林多项式插值公式，将非线性方程按中心差分形式展开，无需计算函数的雅可比矩阵。非线性函数f(x)在x=x¯处展开的2阶斯特林多项式插值公式为：

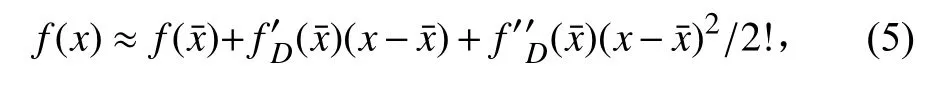
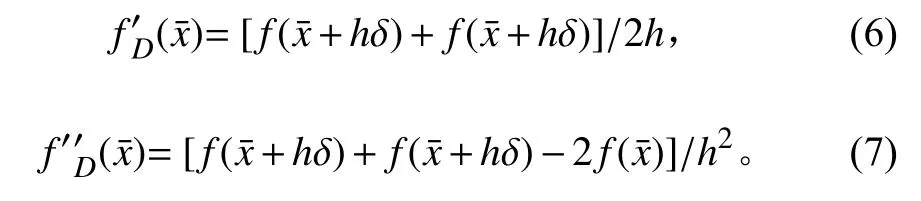
其中：h为中心差分半步长，其取值可决定采样点的分布区间，适合于高斯分布的h最佳取值为为均值为0，与x具有相同协方差的随机变量。式（6）可以看作是用中心差分运算代替泰勒级数展开中的求导运算，用1阶和2阶中心差分算子来代替1阶和2阶导数。

文献[11]中的中心差分滤波器和文献[12]中的差分滤波器都是基于斯特林多项式插值公式，本质上是相同的，也就是CDKF。CDKF通过确定性加权的采样点（Sigma点）来近似状态变量的分布函数，并通过采样点的非线性变换，估计非线性变换后状态变量的均值和协方差。L维的状态向量需要构造个Sigma采样点，Sigma点与真实的状态向量有着相同的均值、方差和高阶中心距。常规CDKF用于目标跟踪的具体步骤如下：

步骤1k=0时，初始化状态向量和协方差

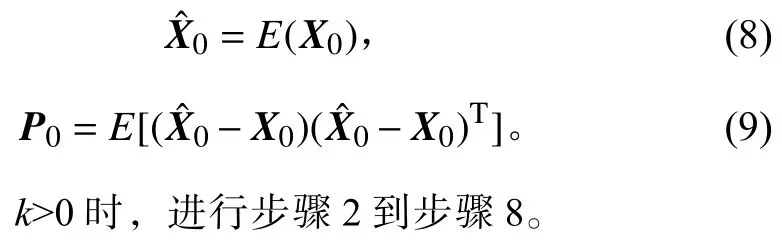
步骤2采样点和对应权值

步骤3时间更新

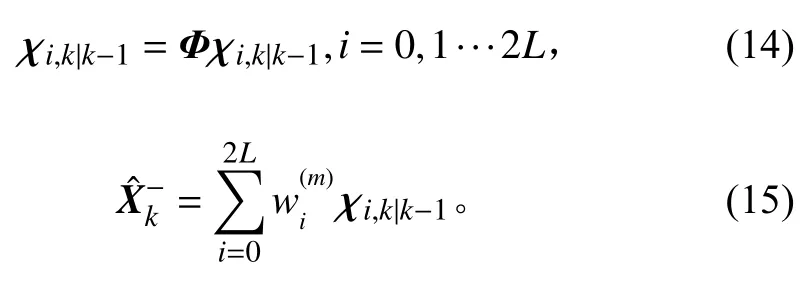
步骤4采样点协方差矩阵

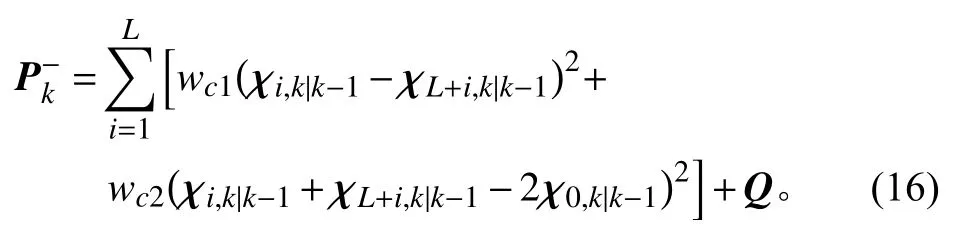
步骤5采样点点集更新

步骤6量测及其协方差更新

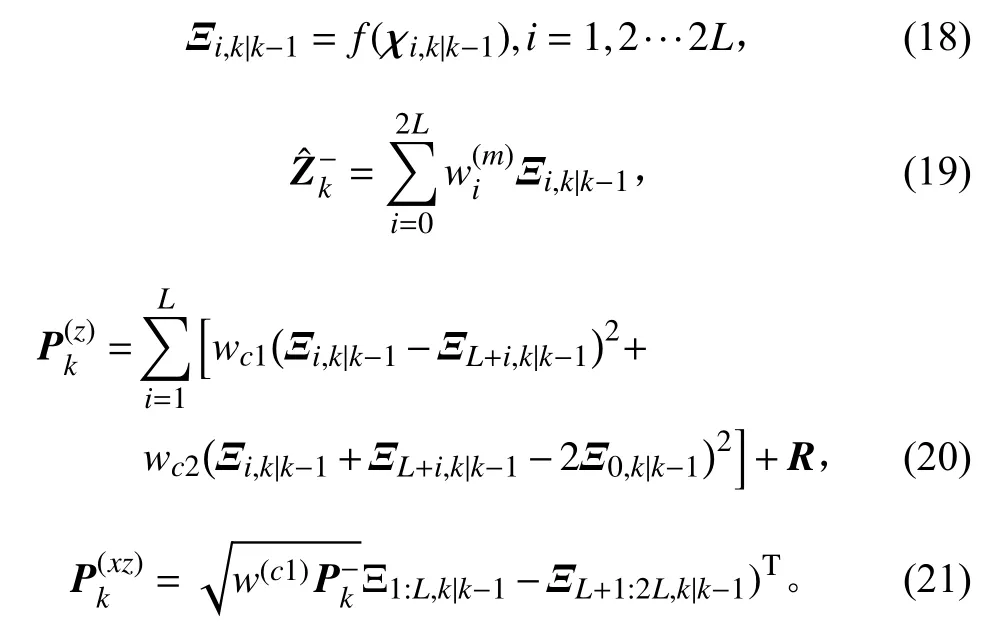
步骤7卡尔曼增益和目标状态更新

步骤8状态协方差更新

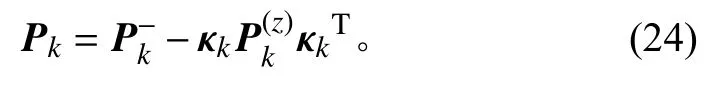
在k=1,2···K时，循环步骤2到步骤8，即可完成CDKF滤波。

2 本文所提方法

CDKF方法是一种应用广泛的确定性采样的非线性滤波方法，但在单站纯方位目标跟踪中，容易出现滤波不稳定甚至发散的情形。为了解决这一问题，本文提出一种奇异值分解平方根中心差分卡尔曼滤波（Singular Value Decomposition Square Root Central Difference Kalman Filter，SVDSR-CDKF）。不同于常规的平方根方法，它在计算采样点的协方差和量测协方差中采用QR分解，而在计算状态协方差更新阶段使用奇异值分解。

2.1 协方差的QR分解

与常规的平方根方法相同，本方法同样对采样点协方差和量测协方差进行QR分解。QR分解可表示为A=QR，它将矩阵A分解为一个正规正交矩阵Q和一个上三角矩阵R的乘积，则容易推导出：

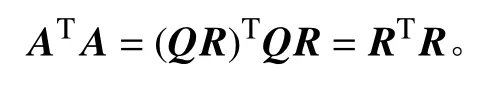
用采样点协方差矩阵QR分解得到的代替，则

其中，QR{}表示QR分解，返回结果为分解后得到的上三角矩阵。用量测协方差矩阵的QR分解代替，则

2.2 奇异值分解协方差平方根更新

常规的平方根方法采用Cholesky分解计算状态协方差的平方根。Cholesky分解要求被分解的矩阵是正定的,而对于纯方位单站目标跟踪，尤其是近距离时，方位噪声扰动大和观测站机动的影响，常规的平方根CDKF在状态协方差平方根更新有时可能出现非正定的情形，导致滤波不能正常进行。奇异值分解不受被分解矩阵正定性的限制，相比于Cholesky分解更加稳定和易于实现。因此本文提出在CDKF的状态协方差更新阶段，用奇异值分解的方法构造状态协方差的平方根。

若A∈Rm×n(m≥n)，则矩阵A的奇异值分解为：

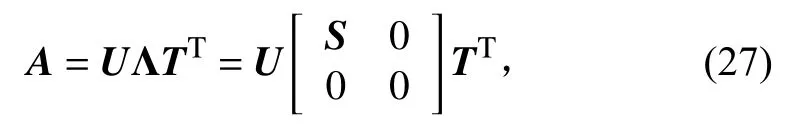
其 中 ，U∈Rm×m，T∈Rn×n， Λ ∈Rm×n，S=diag(s1,s2,······sr)，s1≥ s2≥ ······≥ sr≥ 0是A的奇异值。

单站纯方位目标跟踪系统，状态方程的协方差矩阵为：

P是一个对称矩阵，对其进行奇异值分解后可得U=V，故可得：

然后，对更新后的状态协方差进行奇异值分解：

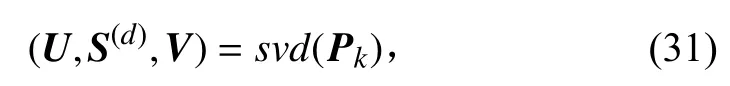
其中，U,S(d),V分别对应式(27)中的U,Λ,T。最后令协方差矩阵平方根为：

用式（30）～式（32）代替CDKF中的步骤8，可以得到一种基于奇异值分解的状态协方差平方根更新方式。由于奇异值非负，因此总是有意义的。即使式（30）的协方差是非正定的，也可以完成奇异值分解，并计算得到Sk。

2.3 奇异值分解平方根CDKF流程

本文所提出的奇异值分解平方根的中心差分卡尔曼滤波方法建立在1.2节所述的CDKF方法的框架之上，具体步骤如下：

步骤1k=0时，初始化状态向量和协方差分解阵

其中，chol代表Cholesky分解。

步骤2采样点及其权值

步骤3时间更新

步骤4采样点协方差的QR分解

步骤5采样点集更新

步骤6量测更新

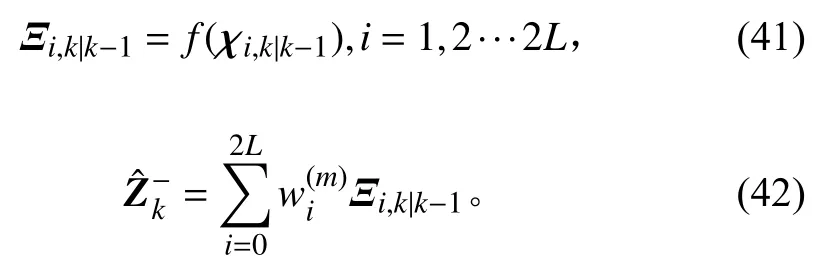
步骤7量测协方差阵QR分解

步骤8卡尔曼增益和目标状态更新

3 仿真实验

为了验证本文所提方法在单站纯方位目标跟踪中的有效性和优势，在3种常见的近距离跟踪轨迹情形下进行仿真。初始状态观测站获取的距离误差5%，速度误差5%，初航向误差的均方差为3°。方位估计周期为100 ms，系统的观测噪声协方差R=3，过程噪声强度。分别用CDKF、常见的平方根类方法SRUKF以及本文所提的奇异值分解平方根CDKF方法进行100次蒙特卡罗实验。

用均方根误差（RMSE）来衡量估计偏差。定义均方根误差如下：

情形1：直线拦截目标轨迹。

目标以50 kn速度向东做匀速直线运动。观测站初始位置坐标为（480，128），以50 kn的速度向南偏西60°方向运动，观测时间10 s。这种情形下的运动态势如图1所示。图2为100次蒙特卡罗实验统计的3种方法的均方根误差比较。

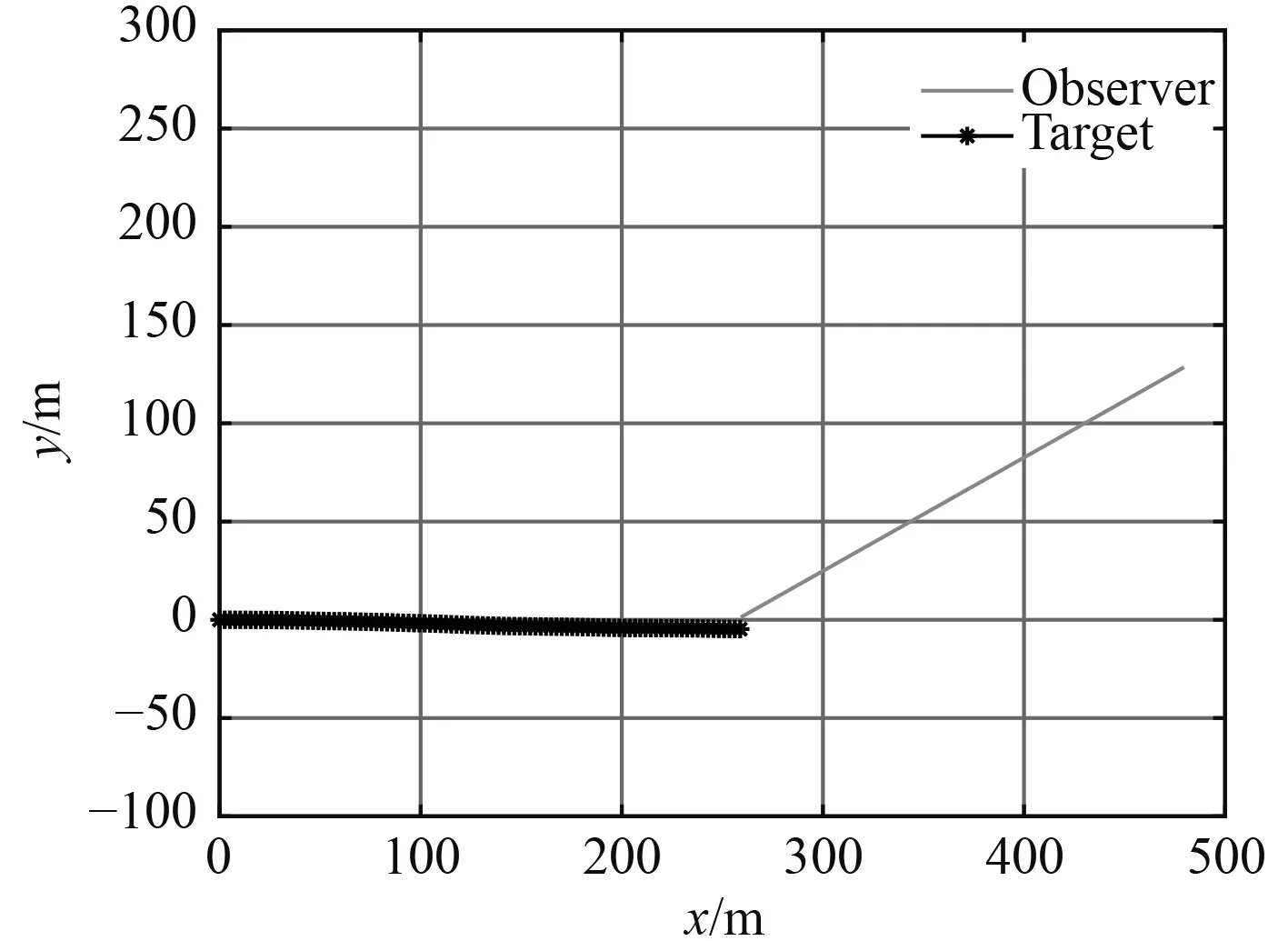
图1 情形 1 运动态势图Fig.1 Movement situation map of case 1

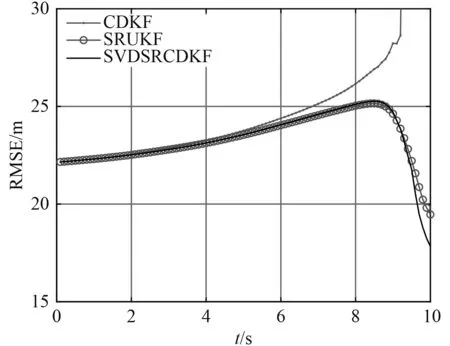
图2 情形 1 均方根误差Fig.2 Root mean square error of case 1

为了验证不同观测噪声协方差下所提方法的有效性，在观测噪声协方差为1°～5°的条件下分别进行100次蒙特卡洛实验，统计3种方法的平均RMSE，结果如表1所示。

表1 不同观测噪声协方差下的各方法比较（情形1）Tab.1 Comparison of methods in different observation noise covariance (Case 1)

情形2：观察者近距离提前角追踪目标。

目标以50 kn速度向东匀速直线运动，观测站在目标北偏东60°方向距目标250 m处，以50 kn的速度、7°的提前角追踪目标，观测时长为7 s。图3展示了这一情形下的目标和观测站的运动态势。统计100次蒙特卡罗实验结果，3种方法的均方根误差比较如图4所示。

在观测噪声协方差为1°～5°的条件下，统计100次实验中3种方法的平均RMSE，如表2所示。

图3 情形 2 运动态势图Fig.3 Movement situation map of case 3

图4 情形 2 均方根误差Fig.4 Root mean square error of case 2

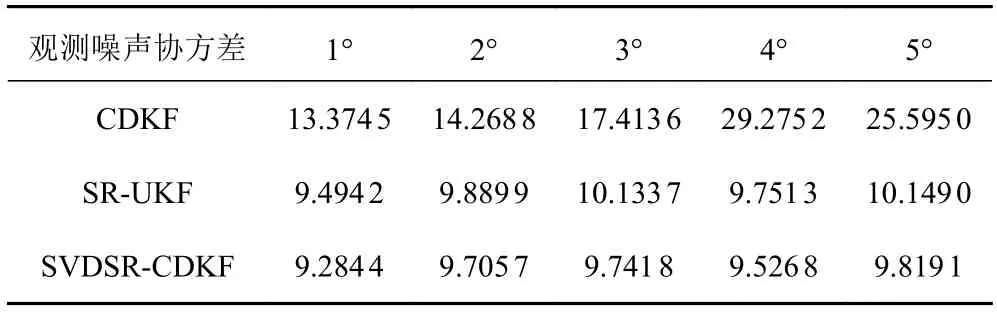
表2 不同观测噪声协方差下的各方法比较（情形2）Tab.2 Comparison of methods in different observation noise covariance (case 2)

情形3：观测站迎面拦截态势。

目标以50 kn速度向东做匀速直线运动。观测站初始位置坐标为（454，145），以50 kn的速度向南偏西45°方向匀速直线运动。8 s后观测站转向正西方向以50 kn速度向目标匀速直线运动，观测时长共计14 s。情形3的运动态势如图5所示。3种方法100次蒙特卡罗实验后的均方根误差如图6所示。3种方法观测噪声协方差为1°～5°时，100次实验的平均RMSE如表3所示。

图5 情形 3 运动态势图Fig.5 Movement situation map of case 3

图6 情形 3 均方根误差Fig.6 Root mean square error of case 3

表3 不同观测噪声协方差下的各方法比较（情形3）Tab.3 Comparison of methods in different observation noise covariance (case 3)

综合3种情形下各滤波器的仿真结果，对于同一目标不同的跟踪轨迹得到的跟踪误差是不同的，这说明对于单站纯方位目标跟踪而言，观测站的机动直接影响估计效果。但实际中肩负其他作业任务的观测站不一定可以执行最优观测轨迹，这对滤波方法的性能提出了更高要求。而3种不同的观测轨迹中，对比3种滤波方法的误差可以得到相似的结论：常规的CDKF方法由于容易出现发散，导致平均误差较大，各种情形下其均方根误差都是最大的。SR-UKF方法作为一种经典的平方根类的方法，用于水下纯方位目标跟踪具有较好效果，各种情形下误差均低于CDKF方法。本文所提的SVDSR-CDKF方法解决了CDKF在几种情形中容易发散的问题，且滤波误差最低。在3种仿真情形下和各种不同的观测噪声协方差下，本文提出的SVDSR-CDKF方法均具有最低的均方根误差。

4 结 语

针对单站纯方位目标分析中有时容易出现的滤波器不稳定、易发散的情况，本文提出一种SVDSR-CDKF方法。该方法以CDKF方法为基础，在计算采样点协方差和量测协方差时采用QR分解计算协方差平方根，而在状态协方差更新阶段使用奇异值分解。通过2种不同的方式计算协方差的平方根代替协方差矩阵参与运算，增强算法的稳定性。为验证所提方法效果，进行了3组不同情形的仿真实验，比较常规CDKF方法、经典的平方根类方法SR-UKF方法和本文所提的SVDSR-CDKF方法，并在每种情形下调整不同的观测噪声进行各方法的均方根误差比较。结果表明，本文所提方法避免了常规CDKF容易发散的情形，且具有比常规CDKF和SR-UKF更低的滤波误差。综合各项仿真结果表明，本文提出的SRSVDCDKF方法是一种精度高、稳定性好的纯方位目标跟踪方法。对于本文的未尽之处，未来考虑在以下方向进行研究：一是探索该方法对于跟踪机动目标的效果；二是考虑该方法对于三维模型中目标的跟踪。