水声定位方法研究进展

吕文红，苑娇娇，侯佳辰，吴 琪，郭银景,3

(1.山东科技大学 交通学院，山东 青岛 266590；2.山东科技大学 电子信息工程学院，山东 青岛 266590；3.青岛智海牧洋科技有限公司，山东 青岛 266590)

0 引 言

水下定位应用广泛，随着国家海洋战略的实施，对水下定位精度的要求越来越高。由于声波是水下信息传输唯一有效的载体，水声定位成为水下定位的主要选择[1]。以基线方式激励的水声定位技术是一种通过测量声波传播的时间、相位等信息实现定位的技术。水声定位系统按应答器基阵基线长度分为长基线（long baseline positioning，LBL）、短基线（short baseline positioning，SBL）、超短基线（ultra-short baseline positioning，USBL）[2-3]，三者的性能比较见表1[4-6]。

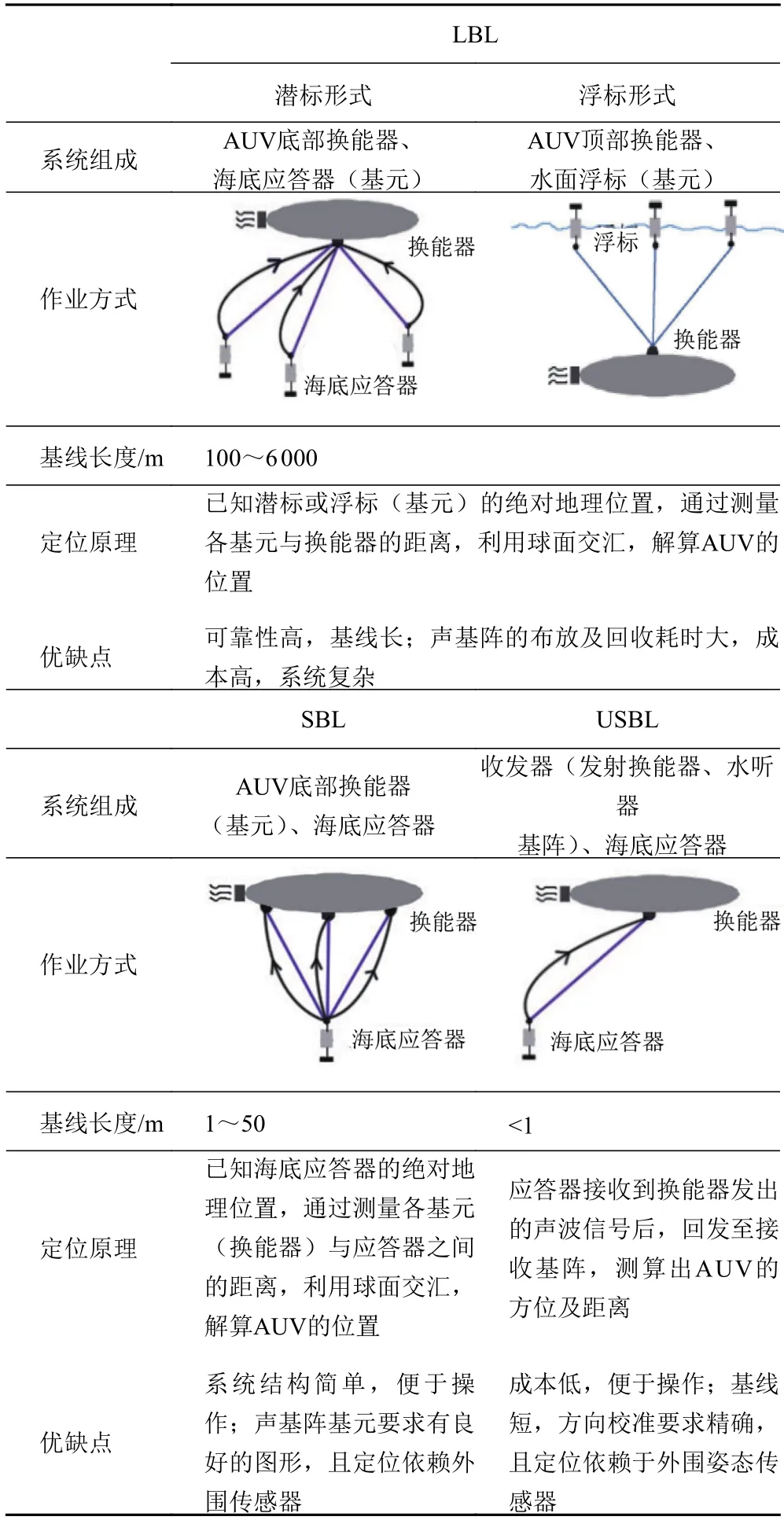
表1 不同基线系统的性能比较Tab.1 Performance comparison of different baseline systems

我国水声定位技术正处于快速发展期[7]，典型代表有中国科学院声学研究所、哈尔滨工程大学等。由于水下环境复杂，基线水声定位精度的研究主要从以下2个方面入手[2]：

1）声速修正

传统基线系统定位的基础是声音沿直线传播，声速是常数，但实际上由于水中声速随空间变化，声音传播路径是弯曲的，不是一恒定常数[8]。声速不确定以及海洋动态环境中的噪声、折射、温度、盐度、水流等都会对基线水声定位精度产生较大偏差[9]。

2）基阵布放合理化

海底应答器基阵之间的位置误差以及海面母船相对于每个应答器的位置误差取决于设备的最初安装精度以及海底基阵的布局。在实际布阵过程中，由于水下环境的影响，通常会存在位置偏差，从而导致的基阵误差，降低定位精度[10]。

1 声速修正方法研究进展

声速修正方法主要分为两类：第1类方法以公式法和查表法为代表，算法简单，计算效率高，但计算容易计算错误，定位精度低；第2类方法以精度较高的有效声速法和声线修正法为代表，应用广泛，但有效声速法需要大量计算，效率低，声线修正法模型复杂，计算量稍大。

1.1 公式法和查表法

泰勒级数展开法和声速经验公式法是早期声速修正公式法的代表。1964年，Vaas[11]提出的泰勒级数展开法是将声速在近似声速处展开成泰勒级数的形式。1987年，Anderson提出的声速经验公式法是海水中温度、盐度和静压力的函数[12]，海洋科学家们相继提出不同海水声速经验公式，共有10种（见表2），每个声速的经验公式都有其特定的使用范围[13]。其中，Chen-Millero-Li公式（1994）是对Chen-Millero公式（1977）的改进，Chen-Millero公式用于海水声速的算法是国际公认的水文数据标准[14]。

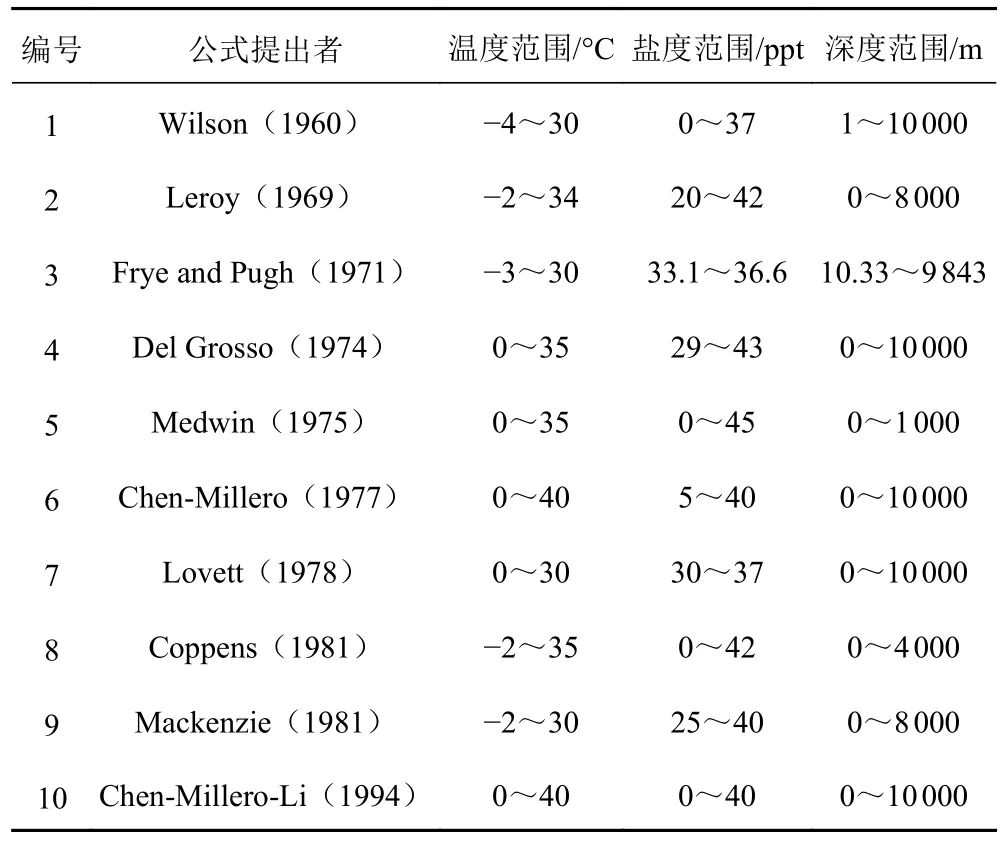
表2 10种声速经验公式Tab.2 10 empirical formulas for sound velocity

2006年，葛亮等[15]提出一种查表法，预先根据深度等控制参数的变化建立声速表格，在定位求解时根据特定的控制参数值采用插值方法获得有效声速，在垂直入射情况下，该方法与泰勒级数展开法相比插值误差缩小近8%，当俯仰角较小时尤为明显。梁民赞等[16]于2009年提出一种声线修正的查表法，与文献[15]中的查表法不同的是：通过建立传播时延、声源与接收机的水平距离的对应关系表，根据所测得的时延值查表得到水平距离值，利用声线在水平面的投影水平距离通过圆交汇解算出目标的位置，避免因使用平均声速使得球面交汇半径同时伸缩导致的解算结果偏差。同时，声速修正表可以离线求出，避免了在线计算，具有良好工程应用性。

1.2 有效声速法

2001年，VINCENT等[17]在深水声学定位研究中首次将海洋空间中任意两点间的声速定义为有效声速（Effective Sound Velocity，ESV），并提出 ESV 的估计方法，但是此方法仅适用于直达波所在区域内ESV的求解。孙万卿[18]于2007年提出一种基于有穷状态自动机的浅海信道ESV估计方法，虽考虑了海面海底反射，但对海面反射考虑得不够充分，以小步长搜索时计算量甚大。阳凡林[19]提出一种基于最小二乘技术的ESV估计方法，利用大量的观测值，可同时定位水下静态目标。对于50～100 m海深中的目标，完成一次位置与ESV估计大约需要5～10 min，此方法无需声速垂直分布先验信息，但带来繁重计算量，对快速获取ESV空间分布的物理图像难以短时完成。

林旺生等[20-21]也曾就浅海信道ESV的估计进行过初步探讨，文献[22]进一步研究浅海信道的ESV，提出一种基于特征射线伪搜索的ESV估计方法，以快速获取信道中任意两点间ESV及其空间分布的物理图像。ESV在垂直维度上的变化率要较水平维度高一个数量级，且在数十米范围内，有效声速变化较小。

2018年，文献[23]建立了一个深海通道模型，通过在该模型上搜索最短延迟特征线，得到最早到达准则下的ESV估计。2019年，文献[24]提出一种基于ESV的声速修正方法，通过全局优化方法中的遗传算法获得包含ESV大部分信息的稀疏ESV表，并从中搜索最优ESV，最小化系统硬件负担、抑制非均匀声速的影响，从而实现实时操作的高精度定位。在现场试验中可将定位的反向均方根误差从5.02 m减小到2.35 m。2019年，黄健等[25]通过分析ESV与目标和水听器相对位置之间的关系，提出一种未知声速下基于粒子群优化（Particle Swarm Optimization，PSO）算法的 LBL 系统定位方法，利用LBL系统中的冗余信息建立多参数优化函数，通过PSO算法解算优化函数的估计ESV对目标进行定位。该方法可在无法准确获得声速剖面的情况下提高LBL系统定位精度。

1.3 声线修正法

声线修正法实质上是基于射线声学的迭代法。1992年，吴德明对LBL平面阵型进行声线修正[26]，利用迭代法逼近计算目标位置。在复杂水文条件下仍有较高计算速度，但将其应用到SBL平面阵型时遇到声线弯曲大的困难。为解决这一困难，文献[27]采用内插法求出合理的声线，并应用差分方程求解迭代的修正量。在相同水文条件和阵形情况下，修正后的定位误差可由未经修正时的数米到数十米降至0.5 m以下。

2002年，王燕等[28]从迭代数值计算角度出发，提出一种适用于LBL水声定位系统声线修正的迭代方法，将水下声速分布近似为分层等梯度分布，用数值解法逐步逼近求出合理的声线和定位点以提高定位精度。该试验是在声速梯度不大的湖上进行的，因此应用环境是定位精度要求不高的定位系统，在复杂水文环境下分层等梯度的声线跟踪方法存在定位精度与计算量的矛盾。结合分层跟踪和等效剖面的思想并针对文献[28]中的问题，张居成等[29]于2013年提出一种自适应搜索可满足定位精度的分层间距的分层方法，并逐层进行声线弯曲补偿。通过非等距划分有效控制了层数，且计算量可减少至原来的30%。2015年，李圣雪等[30]也针对文献[28]中的问题，提出一种自适应分层声线跟踪法，根据声速梯度变化情况对声速剖面数据进行自适应分层，根据阈值大小保留必要的声速层，与文献[29]相比，在保证定位精度的前提下减少了迭代计算时间。

2018年，文献[31]提出一种将恒定声速射线跟踪法和等梯度射线跟踪法相结合的组合射线跟踪法，利用经验正交函数对实时声速剖面进行反演，减少了环境等因素对声速剖面测量的误差。获得声速剖面后，恒定声速射线追踪方法用于声速稳定的区域，而等梯度射线追踪方法用于声速显著变化的区域。在不同入射角和不同深度的情况下，使用组合射线追踪方法相对于恒定声速射线跟踪法的定位误差最小减少了20%，最大减少约为70%。在同深度200 m下，入射角为30°的定位误差为0.4%，而入射角为40°的定位误差为0.6%。

2 基阵改进方法研究进展

USBL阵利用距离测量和同时测量基元间的相位进行定位，不合理的基阵布局设计、微小的安装误差都会造成定位误差。具体改进措施主要有2种：改进基阵间尺寸，加大基阵孔径；改变基阵阵型或增加阵元数量。

2.1 基阵尺寸

传统的USBL定位系统多采用孔径小于半波长的三元基阵来估算目标的位置。由于基阵孔径小导致系统定位精度受限、随机噪声的影响导致测得信号的相位起伏，使得超短基线定位系统在远距离定位时精度不高，信标放在海面以下100 m，接收阵在5 m处，则相位测量偏差为1.4%[32]。为了提高USBL定位系统远距离的定位精度，2006年，喻敏等[33]加大基阵孔径，形成新基阵来提高定位精度。国内传统USBL的定位误差约为3%，利用新基阵所得的定位误差减小到传统基阵的1/8。

多数加大USBL孔径的方法是通过设计有冗余阵元，利用无模糊阵元的相位差[33-34]或相邻阵元间相位差的差分信息[35]来解决孔径增大后的模糊问题。而郑翠娥等[36]于2009年提出一种基于双脉冲的相位解模糊方法且无需冗余阵元的改进阵型。在南海一水深约为110 m处，用小间距基元组定位得到的坐标，其北方向标准差为22.46 m，东方向标准差为24.67 m；而用基于双脉冲抗模糊方法的改进阵型定位得到的坐标，其北方向标准差为4.74 m，东方向标准差为5.09 m。马根卯等[37]于2016年主要针对USBL成阵后基元本身的位置进行精确校准和测量，从对角基元的间距（孔径）测量、角度测量、高度差测量三方面进行误差分析，进而采用稳态波形相位差法测量，为USBL提供精确位置校准数据。

2.2 基阵阵型和阵元数量

传统USBL定位系统的阵列设计研究主要为四元十字阵列和四元正四面体阵列。通过改变阵型设计或增加阵元数量后，利用冗余的时差信息，可获得更高精度定位。2003年，陈华伟等[38]针对四元十字阵定向和定距精度受目标方位影响这一缺点，提出五元十字阵列的声目标定位方案。十字平面阵对三维空间定向精度较高，但对稍远一点的目标定距误差较大且定位误差大的区域较多，这是平面阵的基本特点。对此，2006年，孙书学等[39]利用正四棱锥定位，形成空间序列，与平面阵相比，该阵能有效对近距离目标定位且降低了声阵列的盲区，但定距精度受仰角的影响较大；针对四元平面方阵定距精度差和文献[39]存在的缺点，2008年，林晓东等[40]通过设计六元阵列减小了仰角对定位结果的影响，当声目标位于仰角为10°～80°的水域范围内时具有较好定位性能。Arkhipov[41]于2012年通过设计基于五顶点凸多面体（正方形金字塔）的五元USBL接收阵列在大范围俯仰角和横滚角内均为可靠操作。阵元数目的增加可以提高定位精度，但同时意味着系统复杂度、成本的增加，即阵元数目与所需定位精度之间存在一个折中方案。因此阵元数目及阵型结构对定位精度的影响是一个非常值得讨论的问题[35,42]。针对这一问题，南德等[43]于2019年利用定位误差的克拉美罗下界作为评价指标，对阵型结构及阵元数目进行优化，确定优化的九元立方体阵列，并利用梯度下降法实现平台轨迹优化，使得系统最快收敛到需要的定位精度。在1 000 m内，利用优化轨迹可以将定位均方根误差快速收敛至预设的0.2%以内。此外，对于海试实验采集数据的目标定位结果显示，对距基阵约700 m及400 m的目标，五元阵定位标准差相较四元阵缩小了约2 m及1 m。

3 结 语

水声定位是AUV水下目标定位的重要研究领域，具有广泛的应用前景。在声速修正方法中，数值法（公式法和查表法）算法比较简单，效率较高，但其定位精度比有效声速法和声线修正法的定位精度低，适用于所需定位精度不高的应用环境；有效声速法需要大量计算，效率不高；声线修正法模型复杂，计算量也稍大；有效声速法和声线修正法定位精度较高，近几年大量声速修正方法研究主要集中在这2种方法的改进上，如有效声速法中如何搜索最优ESV。

在基阵的2个具体改进措施中，加大基阵尺寸形成新基阵，能有效减小定位误差，但由于安装不太方便会带来安装误差。通过改变基阵阵型或增加阵元数量可获得更高精度定位，但同时意味着系统复杂度、成本的增加。比较2个措施，阵型阵元改进与所需定位精度的折中方案更具发展潜力。

为了达到更高精度水声定位，今后的研究方向有以下几个方面：

1）遗传算法和PSO算法的组合用于优化稀疏ESV表。在基于ESV的声速修正方法研究进展中，通过遗传算法、粒子群优化算法等一些全局优化方法获得包含ESV大部分信息的稀疏有效声速表，并从中搜索最优ESV，从而实现实时操作的高精度定位。遗传算法通过定义成本函数来搜索参数，这使得搜索过程变得简单。搜索过程可能是并行的，可以同时比较多个个体，使其更加强大。然而，遗传算法的缺点是在面对高维问题时搜索效率较低。在PSO算法的每个进化过程中，只有最优粒子才能将信息传递给下一代，这使得搜索速度非常快，但同时也容易陷入局部最优。此外，PSO算法难以有效地解决非直角坐标系中的优化问题。将两者算法优势互补，遗传算法和PSO算法的组合将会是未来提高定位精度的研究方向之一。

2）针对超短基线易受水声环境以及阵元制造、安装等外界因素的影响、远距离定位精度低等问题，许多研究者从不同方面改进定位方法，如通过加大基阵孔径来提高定位精度。但阵元数越多，定位误差越受制造、安装等外界因素影响。因此如何在阵元数较少的情况下，本着减小阵元制作难度，降低布放成本的原则，通过优化不同阵元间距来提高超短基线的定位精度是进一步研究的方向之一。

3）基于组合基阵定位系统辅助的声速修正算法。2017年，针对水下定位系统误差存在随时间累积、GPS系统无法在水下定位以及传统LBL系统复杂等问题，张涛等[44]建立了惯导、DVL（Doppler Velocity Log）和三阵元基阵定位的距离耦合组合导航模型，提出一种基于组合导航系统模型辅助的等效声速修正方法。当AUV深度未知时避免了求解位置时的模糊问题，同时在深度30 m内能有效修正误差，且定位误差小于4 m。该算法还不够成熟，为使水声定位系统的定位误差更小，基于基阵设计的定位系统辅助的声速修正算法还有待进一步研究。