基于遗传算法的南京周边城市旅游规划研究

王梦甜

(南京财经大学，江苏 南京210023)

一、引言

随着总体国民经济水平和人均收入水平的不断提高，我国社会的主要矛盾已经转化为人民日益增长的美好生活需要和不平衡不充分的发展之间的矛盾，生活的质量成为当代人们普遍追求的目标。同时人均汽车拥有量的增多使得很多家庭在短暂节假日的时候选择去周边城市旅游，这推动了旅游业和经济的发展。有效的路径规划成为出门必备，如何以最短的距离、最小的成本游玩周边城市成为问题，对于提高居民的生活质量水平具有重要意义。旅游路线规划问题来源于数学领域中经典的旅行商问题(TSP)，同时也称为旅行推销员问题或者货郎担货问题，不仅有理论价值，同时也非常有实际价值，目前广泛应用于物流行业货物配送、智能化交通道路控制、网络路由和计算机等相关领域。旅行商问题(TSP)是数学组合优化问题中典型NP-Hard问题，在小规模下计算好解决但是在大规模的情况下，无法运用传统数学办法计算。对于旅行商问题目前解决方法一般主要包括两种:完全算法解和近似方法解。完全算法指在有限的计算步骤下可以找到问题的最优解，例如经典的分值定界法、Dijkstra算法、动态规划算法等，但是这种算法缺点在于时间复杂度过高，尤其目前大数据时代无法满足大规模的数据运算需求。近似算法解指可以在多项式时间内结束，从而得到问题的一个近似解，这种算法相对于前者更优且在实际问题中应用更多，目前研究和应用较多的启发式算法主要为粒子群算法、蚁群算法和遗传算法等。纵使有这两种算法，但是学者们仍然没有寻找到一个解决TSP问题的完美方案。在这方面的研究很多，国内学者们也取得了较多成果。高海昌等人综述了蚁群算法、遗传算法等一系列智能算法，让人对这些算法有了一个较为清晰的认识；李玮对使用的遗传算法中编码部分采取矩阵编码方式解决TSP问题；姚明海等主要采取将遗传算法和其他智能算法相结合的方式解决问题；雷玉梅等对遗传算法原理进行介绍并且分解进行；吴阳等人通过对遗传算法的改进研究共享汽车停车点布局，并用MATLAB求解得到最优解；张玺君等人针对目前出租车运行过程效率低下问题，基于改进遗传算法构建了出租车共乘线路规划模型，最终可以快速得到优化路径；徐晨畅和钱松荣基于遗传算法建立突发公交智能调度并给出相关支援方案；张惠彬等利用构建了事故发生时人员疏散路径优化并用遗传算法进行求解。旅行商(TSP)模型用于旅游路径规划也有一些成果，吴凯在理论上将定性和定量两种方法结合进行旅游路线设计；刘倩等利用蚁群算法对景区内车辆调度进行路径规划；王慧等为满足旅游爱好者，设计出遍历全国所有5A级景点的旅游路径规划并用蚁群算法求解；徐书杨等考虑景区内部拥挤度、景点热度等因素使用蚁群算法规划景区路径，从而提升旅客旅游体验。文章基于目前研究状况，以江苏省南京市为中心，距离最短为目标函数，通过经度、纬度来研究其周边共8个省会城市或直辖市(上海、南京、合肥、杭州、武汉、南昌、郑州、济南)出行旅游最短路径，并且利用遗传算法对其进行求解，结果证明遗传算法在解决周边游路径规划问题方面具有较高的实用性。

二、旅行商(TSP)问题描述

旅行商(TSP)问题是制定多个城市地点并且知道每两个城市之间的距离，旅行商人随机选择其中一个城市作为起点出发，对所有城市进行访问并且只访问一次同时回到最初的城市，寻求最短距离的完整回路。在运筹学中可以用图论中的无向图进行解释，如无向完全图A＝(V，E，r)，要求遍历A中每一个节点并且形成简单的回路，使各边权重相加之和最小，其中V＝{1，2，…，n}是无向图中的每个节点集，表示被访问的城市，E是连接V中两个不同点之间的边集，r表示两城市之间的权重即距离。其数学模型定义如下:

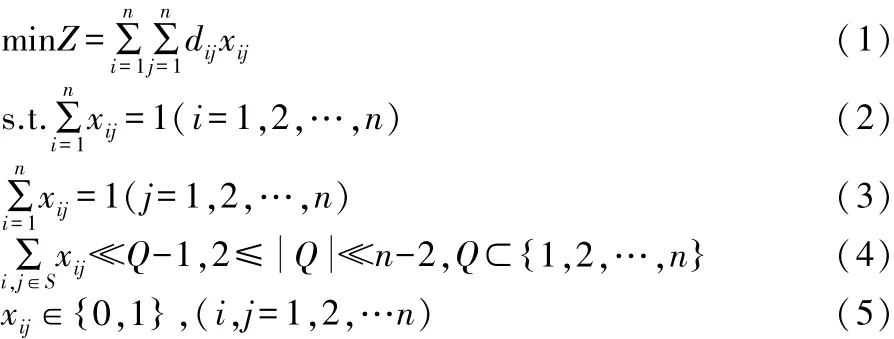
上述中(1)式为所求的目标函数，即旅行商所经过路径最小值，其中dij表示城市i到城市j的两地距离，也就是图论模型中的r值，在文中距离是利用两个城市的地理坐标(经度、纬度)进行转化计算得到；(2)式和(3)式表示旅行商有且只经过一次其中的每一个城市；(4)式表示旅行商在整个过程不能形成循环的路径；(5)式表示是否去过这个城市，用xij＝0表示旅行商未曾经过该城市，xij＝1则表示旅行商已经去过的城市。

三、遗传算法模型构建

遗传算法想法来源于自然界，是继承了生物学中的遗传思想“优胜劣汰” ，模仿自然界生物的进化机制，将自然界生物的繁殖、交配以及基因突变等相关概念引入整个算法过程，实质上是一种并行且高效的全局搜索方法。遗传算法在寻求最优解的过程中能够自动获得关于整个搜索空间的知识，并且能够很好地改变自己的搜索过程从而获得整个问题的最优解。遗传算法主要原则还是根据生物学中的适者生存，在所有可行解中找到一个近似最优解，而且后面的每一代遗传过程中根据个体在该环境下的适应度再进行选择从而得到一个更优解，这个新个体相对于原来的个体能够更好地适应环境。遗传算法目前是较多领域中获取最优解的一种启发式算法。

文章在构建旅行商问题模型和了解遗传算法相关知识基础上采取了具体的遗传算法，主要步骤如下:

Step1:编码。在一般问题中，多数学者在使用遗传算法的时候会采取二进制编码，但是本文在TSP问题中采取顺序表示的编码方式，顺序中每个数字代表一个城市，不同顺序经过城市连起来为一条新染色体即为一个解。论文以南京周边8个省会城市或直辖市(上海、南京、合肥、杭州、武汉、南昌、郑州、济南)为例，城市编码选取为1～8的数字，假如生成的染色体序列号为12345678，则代表旅行商人从城市1出发依次经过城市2、3、4、5、6、7、8最终再回到出发点城市1的一条回路路径。

Step2:初始化。随机选择一些数量的个体(文中初始数量为100)组成最初的种群即初始解。

Step3:评估。初始化的个体优劣程度是不一样的，为了使最终结果更优，在每次选择的过程中要选择最优个体，因此在评估阶段使用函数来评判个体的适应度决定其优劣程度，从而为下一步个体选择提供依据，通常适应度函数是由目标函数转化而来，文中目标函数是求解最小值，则使适应度函数值最大，因此采取目标函数的倒数值作为适应度值即可，因此适应度函数设置如下:

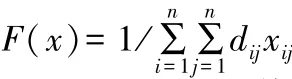
Step4:选择。遗传算法中选择操作是使用轮盘赌的方式，从上一代种群中选择出较好的个体来进行繁衍子代，个体被选择的概率值与其适应度值相关，根据Step3得到适应度的值，个体适应度值越高其被选择到的概率则越大，个体i被选择的概率为P，其中m为初始化的种群数量。计算公式如下:

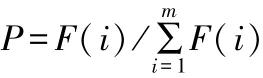
Step5:交叉操作。基因交叉产生后代，将上一步选择的两个个体作为父代进行交叉操作以产生新的子代，文中操作方法是在[1，8](共8个省会城市)之间随机选取选取两个整数r1和r2，将两者之间的部分交换，文中设置的交叉概率为Pc＝0.7。

Step6:变异操作。指在新产生的个体上进行突变的操作，主要维持种群子代的多样性，具体方法是在[1，8]区间上随机选择两个数r1和r2，然后将个体上这两个数字交换，从而得到变异个体，文章实验中变异概率设置为Pm＝0.02。

Step7:结束。文章的终止条件为算法收敛准则是否满足，如果满足各步骤则输出相应的结果，否则返回至Step2进行循环迭代直到最终输出结果。其主要流程图见图1:

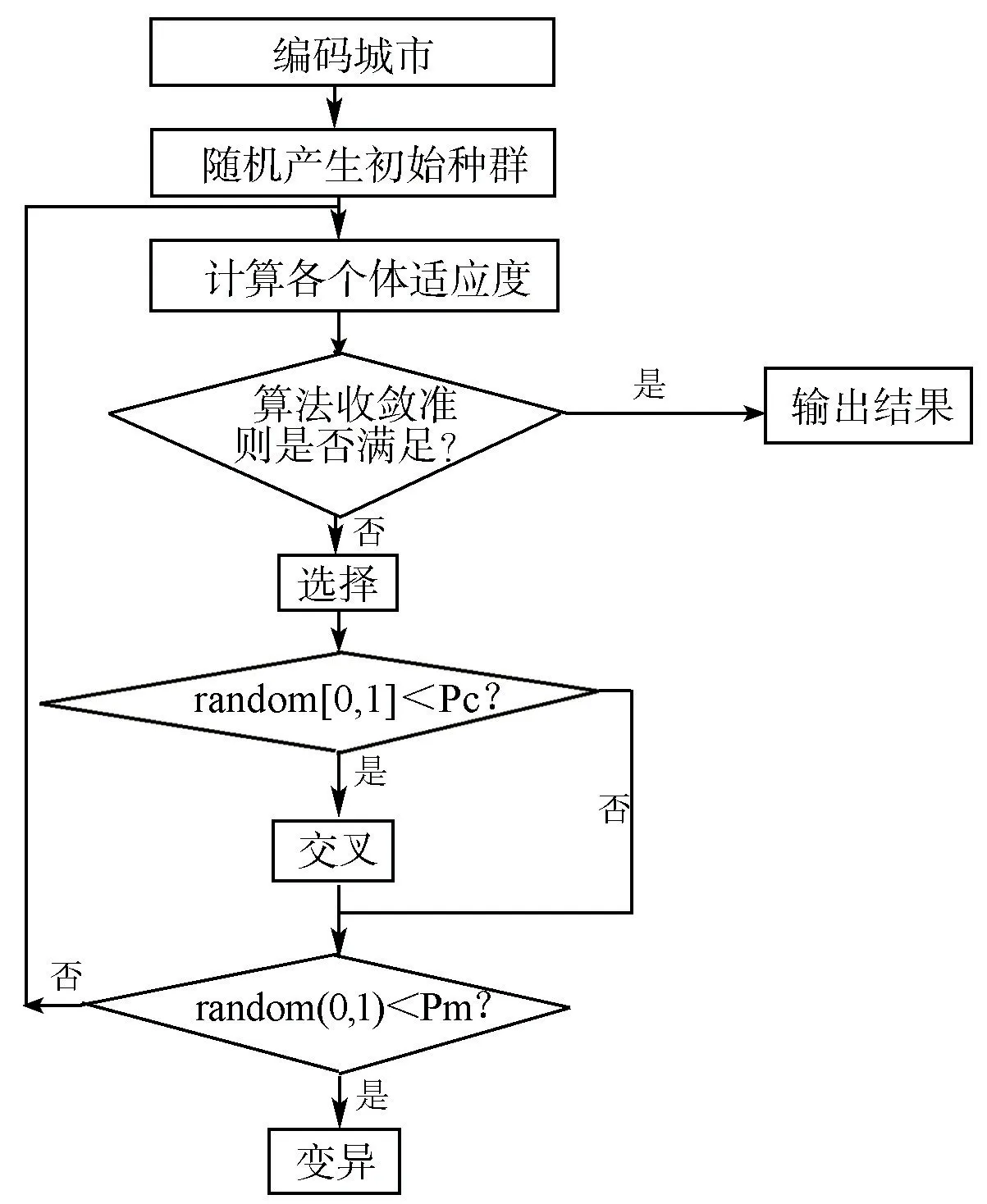
图1 遗传算法流程图

四、实验结果及分析

根据上面所构建的模型和具体的遗传算法步骤，文章基于Python语言对遗传算法进行代码实现，利用遗传算法对模型求解。首先获取8个省会城市或直辖市(上海、南京、合肥、杭州、武汉、南昌、郑州、济南)的地理位置坐标，通过对地理位置的转化求解8个城市先后游玩的最短距离。

在设定的参数以及算法收敛原则情况下得到最优结果为25.943488，具体路径为南京—合肥—杭州—南昌—武汉—上海—济南—郑州，具体路线图如下图2所示。综上所述，南京周边8个省会城市旅游最短路径得以解决，可见遗传算法对于解决南京城市周边游路径规划问题效果显著，对上述八个城市居民采取周边游都具有很好的建议；但是论文仍有不足，第一，各城市数据采取的地理经纬度导致最终距离很小，这与真实地图数据有点差距，但是整体结果符合真实地图；第二，本实验中是将遗传算法中各参数固定，但是对于不同的参数可能会出现不同情况，综上这些不足在未来实验中可以继续改进。

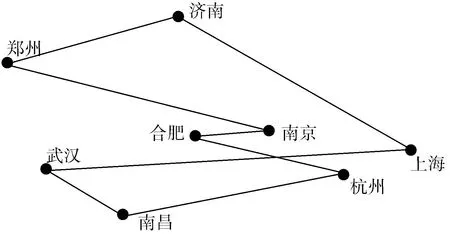
图2 最短路径图