浅谈信号与系统课程中的谱概念
杨利军 杨晓艺 赵晨萍


[摘 要]在信号与系统课程中,存在多个与谱有关的概念,例如频谱分析、幅度谱、相位谱、能量谱和功率谱等,在教学过程中,这些概念常常让学生感到疑惑,不清楚在什么情况下使用合适的概念去分析信号。针对该问题,项目组对信号与系统课程中出现的谱概念进行总结归纳,并给出相应的实验分析,帮助学生理清这些与谱相关的概念之间的关系,为其学习起到一定的指导帮助作用。
[关键词]信号与系统;频谱分析;幅度谱;相位谱;能量谱;功率谱
[中图分类号] G642 [文献标识码] A [文章编号] 2095-3437(2021)02-0115-03
信号与系统课程是电专业和非电专业(如通信与信息系统、自动控制、电子信息、信号与信息处理、计算机和生物医学工程等学科专业)本科生必选的专业基础课。该课程属于理论和应用背景都比较强的专业基础课。Fourier级数和Fourier变换是信号与系统课程中的重要学习内容,在信号分析领域占据着举足轻重的地位。
一、Fourier级数和Fourier变换[1]
我们知道,对于周期为[T]的周期函数[f(t)],当它满足狄里赫利(Dirichlet)条件时,可以展开成如下形式的Fourier级数:
绝对可积是函数Fourier变换存在的充分条件而非必要条件,引入广义函数的概念后,许多不满足绝对可积条件的函数也能进行Fourier变换。
所谓的频谱分析,也称为频域分析,是指通过Fourier变换将信号变换到频率域内对其进行分析,分析的工具是以频率[ω]为自变量的各种物理量,幅度谱、相位谱、能量谱和功率谱就是这样的物理量,对信号的频谱分析其中就包含了对这些谱函数性质的研究。
二、幅度谱、相位谱、能量谱和功率谱
由上述(1)式可知,周期信号[f(t)]可分解为许多虚指数信号[ejnΩt]之和,其对应各分量的幅度为[Fn],而[Fn]为复数,因此可写为
从而,幅值[Fn]、相位角[φn]均为[n]或([nΩ])的函数,分别称为周期信号[f(t)]的幅度谱(也称为振幅谱)和相位谱,其含义为幅度谱[Fn]刻画了不同频率分量(频率[nΩ]随[n]的变换而变化)的幅值随频率的变化情况,相位谱[φn]刻画了不同频率分量的初相随频率的变化情况。易知,[ Fn]为双边谱,且周期信号的幅度谱和相位谱均为离散函数。
由(3)式,非周期信号[f(t)]也可近似看作是分解为不同频率的虚指数信号[ejωt]之和,与(1)式不同之处在于这里的频率[ω]取连续值,称[Fjω]为[ f(t)]的频谱密度函数或频谱函数,[Fjω]是一个复函数,可写为
称[|Fjω|]为非周期信号[f(t)]的幅度谱,[φω]称为非周期函数[f(t)]的相位谱。由于这里的频率[ω]取连续值,因此非周期信号的幅度谱和相位谱均为频率的连续函数。
要理清能量谱和功率谱这两个概念,需要先弄清楚能量信号和功率信号这两个概念。根据教材[1],信号能量定义为在区间[(-∞,+∞)]中信号[f(t)]的能量,用字母[E]表示,即
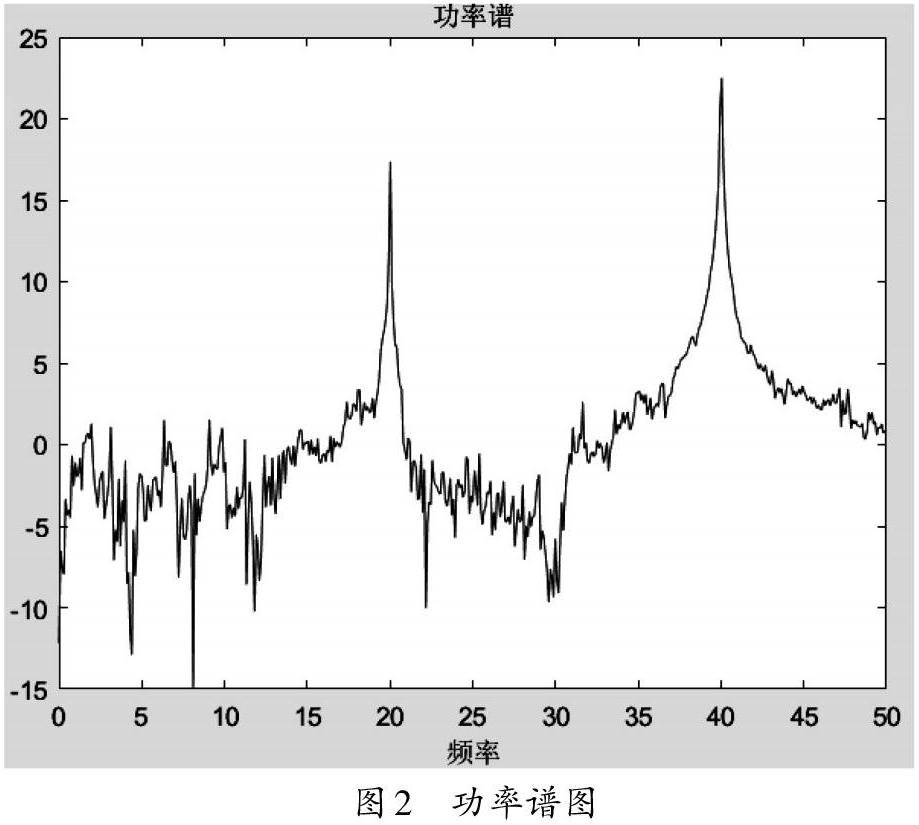
若对于信号[f(t)],其能量满足[0 能量谱(也称为能量谱密度)是针对能量信号而言的,是指用密度的概念表示信号能量在各频率点的分布情况。能量信号[f(t)]的能量谱是该信号幅度谱的模的平方: 著名的Parseval定理(也称为能量守恒定理)告诉我们,信号的时频域能量相等,即如下式成立 从而对能量谱在频域上积分就可以得到信号的能量。 功率谱(也称为功率密度函数)是针对功率信号而言,是指用密度的概念表示信号功率在各频率点的分布情况。由于功率为能量在所作用时间上的平均,因此功率谱在定义的时候需要借助截尾函数[fTt:] 则功率信号[f(t)]的功率谱密度定义为 其中[FT(jω)]为信号[fTt]的Fourier变换。功率谱的推导公式相对复杂,但根据维纳-辛钦定理可知:信号的功率谱和信号的自相关函数是一个傅里叶变换对,因此可以通过自相关函数来求功率谱[2]。 对于非周期的确定性信号(为能量信号),常用能量谱来描述。而对于随机信号(为功率信号),由于持续期时间无限长,不满足绝对可积与能量可积的条件,因此不存在傅立叶变换,所以通常用功率谱来描述。周期性的信号,也同样是不满足傅里叶变换的条件,因而常用功率谱来描述。只有如单频正弦信号等很少的特殊的信号,在引入[δ](delta)函数之后,才可以求解信号的傅里叶变换。 三、实验分析 在本小节,我们基于MATLAB软件给出相关谱概念的实例,从可视化的角度理解这些概念。由于能量谱是幅度谱的平方,因此,这里只给确定性信号的幅度谱和相位谱,以及随机信号的功率谱的实验结果。 实验1 绘制信号[gt=0.5sin40πt+2sin (80πt)]的幅度谱。 在本例中,采样频率为[fs=100Hz]。图1(a)给出了信号[g(t)]的频率在[0~50Hz]范围(奈奎斯特采样频率为[50Hz])的幅度谱图,从图中可以清晰识别到信号的两种频率成分:[20Hz]和[50Hz]。图1(b)是对应的相位谱图。 本实验的MATLAB的代码如下: 图2中,虽然信号受到了随机噪声的干扰,信号[h(t)]的谱图有很多毛刺,但从功率谱图上还是可以清晰识别出信号的两种频率成分:20Hz和50Hz。本实验利用了维纳-辛钦定理来计算信号的功率谱。 本实验的MATLAB代码如下: 四、结论 本文针对信号与系统课程中学生易混淆的几个与谱相关的概念进行总结归纳,并给出相应的MATLAB实验可视化地理解这些概念,便于学生理清相关谱的概念以及各概念之间的关系,指导帮助学生的课程学习。 [ 参 考 文 献 ] [1] 吴大正主编.信号与线性系统分析[M].第四版.北京:高等教育出版社,2005. [2] Alan V Oppenheim,Alan S Nillsky,S Hamid Nawab.信号与系统[M].第二版.刘树堂,译.北京:电子工业出版社,2013. [3] 郑君里,谷源涛.试谈“信号与系统”课程理论与实践之结合[J].电气电子教学学报,2014(3):1-5. [4] 王法松.“信号与系统”课程中关于信号相位谱的分析[J].微型电脑应用,2018(9):1-3. [5] 孙明.基于GUI的周期信号频谱分析演示系统设计[J].实验室科学与技术,2018(1):18-21. [责任编辑:黄紧德]

