考虑回收品质量可控的再制造闭环供应链决策

路正南，杨 鹏

(江苏大学 管理学院，江苏 镇江 212013)

如何协调人与资源、环境三者间的关系，是目前社会发展过程中必须兼顾的重要问题。资源的粗放式利用、废旧产品不合理的处理方式等加剧了人与资源环境之间的矛盾。在全球越来越关注可持续发展理念的大背景下，废旧品回收再制造俨然成为了一个有效的解决方案，回收再制造将有限的自然资源进行回收利用使其价值最大化，能有效缓解经济发展造成的资源浪费与环境污染问题，并一定程度上扩大企业经济效益与社会环境效益。由于消费者对产品的使用程度以及产品初始设计等多方面的差异，用于再制造的回收品的质量残余价值具有一定的不确定性，使得企业的再制造决策存在一定的风险。

1 文献综述

张焕勇等[1]根据消费者的行为习惯将其分为不同的群体，以碳配额为主要相关因素，分析再制造闭环供应链中制造商的生产策略。Vadde等[2]考虑单种和多种产品回收，假设所有的回收都是可以接受的，提出回收产品零部件在不同质量水平下的定价模型，并对主动收购策略和被动收购策略进行比较。肖敏等[3]基于消费者的绿色偏好，构建有无政府补贴机制下的闭环供应链Stackelberg博弈模型，求解模型得出各参数的最优解。Ferrer等[4]则从两种产品的生产成本与市场接受程度出发，构建博弈模型，研究了该过程中的生产与定价策略。李芳等[5]在非对称信息的背景下考虑将新产品与再制品差别定价，研究不同决策方式下供应链中各节点企业的定价问题。高举红等[6]考虑到市场消费者的环保意识，对市场消费者进行分类，并以此为基础构建动态的博弈模型，研究了供应链的决策问题，并分析消费者环保意识对供应链决策的影响。程发新等[7]提出政府的差别补贴政策能够有效提高回收再制造率，并考虑消费者绿色偏好，构建模型研究供应链的定价问题。梁工谦等[8]考虑到市场上关于再制品的需求与回收量存在双重不确定，研究闭环供应链中制造商关于两种产品产量的平衡决策。

以上文献主要都是在碳减排、需求不确定、信息不对称等背景下对再制造闭环供应链的决策问题展开研究，甚少有将回收品质量这一不确定因素综合考虑进来。Ferguson等[9]将回收品的剩余可利用率按0-1进行评级，假设废旧品质量服从正态分布，研究再制造闭环供应链中的回收与生产决策。程发新等[10]将政府为鼓励回收再制造提出的补贴政策，研究了供应链的生产、回收与定价决策。Mukhopadhyay等[11]对于回收再制造过程中废旧品的回收量与可利用价值率进行综合考虑，研究回收与再制造的决策问题。Chen等[12]考虑消费者为价格敏感型群体，将新产品与再制品的价格及需求进行区分，且探讨了需求与价格两者之间的关联，研究该情景下的制造与再制造策略。韩梅等[13]全面考虑双重竞争及回收品质量不确定双重因素，研究闭环供应链中各节点企业的定价问题，并分析回收品质量对回收价、回收率等各参数的影响。Atasu等[14]按废旧品的可利用率将其分为不同的再利用层次，在此基础上研究制造商的制造与再制造决策。黄帝等[15]将废旧品质量与再制造产出率联系起来，以此反映废旧品质量，构建废旧品质量与再制造成本间的直接联系，研究了制造企业的回收与再制造策略。

以上文献基本都是假定回收品质量随机，没有考虑到回收品质量可控这一情境。Govindan等[16]对当前涉及回收再制造的相关研究成果进行文献综述，指出关于回收再制造的研究考虑到的影响因素较多，如碳减排、消费者绿色偏好及其他相关不确定因素等，关于不确定性方面的成果有待继续丰富。李丽君等[17]考虑双边道德风险，提出制造商检测出回收商回收未达质量标准的废旧品时，对回收商进行惩罚的质量控制手段。熊中楷等[18]假设在再制造闭环供应链中，销售商兼为回收商的角色，提出以质量抽检和惩罚系数对销售商的回收行为进行约束与引导，研究制造商效益最大下的抽检比例与惩罚系数。本文借鉴相关研究的理论成果与研究方法，考虑回收再制造过程中回收品质量可控这一情境，并引入相关控制参数，构建了由制造商主导的决策模型，探讨了不同决策条件下的最优生产及定价决策问题。

2 问题描述与假设

本文主要基于回收品质量可控这一情境，研究再制造闭环供应链的决策问题。为方便研究，构建由单一制造商和经销商组成的再制造闭环供应链网络。其中经销商以价格w从上游制造商处批发一定数量的产品，再以零售价p对外售出。此外，本文借鉴Savaskan等[19]研究结论，假定销售商同时兼回收商，从市场回收一定数量的废旧品转售至制造商。回收商从消费者手中以价格pr=(1−t)pm回收总数为Q=h+kpr的废旧品，其中，t∈(0,1)，表示销售商回收活动的单位利润率，h、k分别表示消费者的主动绿色偏好和其对回收价格的敏感系数；制造商再以价格pm=p0+sq从销售商手中回购废旧品进行再制造，其中，p0为制造商回购的最低价格；s为价格随质量的敏感系数。新产品量为Qn=D−Q，Cm、Cr分别表示新产品和再制品的单位生产成本，且Cr=Cm−λq，其中λ＞0，表示成本随质量的敏感系数。

本文以D(p)=α−βp来刻画市场需求，其中， α、β分别表示最大需求及价格对于需求的影响因子。本文借鉴Chao等[20]的研究，将质量投入成本函数定义为I=ξq2，以此来刻画销售商的回收投入。此外，以奖励函数L=ηq来引导销售商回收更高质量的废旧品。综上描述，本文所研究的再制造闭环供应链网络结构如图1所示。

图 1 质量可控下再制造闭环供应链网络Figure 1 Diagram of remanufactured closed-loop supply chain with controllable quality

为简化研究过程，本文对模型作出了以下假设：

1) 市场完全开放，供应链中信息完全共享，无牛鞭效应；

2) 消费者对新产品和再制品的接受程度不存在差异；

3) 不存在库存成本、缺货成本；

4) 供应链中不存在内部竞争。

3 模型构建与求解

本文研究所涉及到的参数及定义如表1所示。

表 1 模型参数及定义Table 1 Parameters and definitions in the model

3.1 分散决策

分散决策下，销售商和制造商作为独立决策者，仅考虑自身利益最大化。在该决策条件下，制造商为引导回收商回收利用率更高的废旧品，制定奖惩措施，而回收商为应对制造商制定的奖惩措施，权衡利弊之后，会付出一定的回收投入来提高回收品的质量。据上述，构建分散决策条件下制造商的期望利润函数为

构建分散决策条件下销售商的期望利润函数为

该博弈过程中，制造商属于主导方，制定商品的批发价与废旧品的回购价，销售商则会以批发价为依据，结合自身利益来确定对外售价及废旧品的市场回收价。销售商可以控制的参数是产品零售价p和回收价 pr，批发价 w和回购价 pm则是由制造商决定， p 和 pr是销售商在考虑自身利益最大化的前提下，以制造商的决策为基础来制定的。故而本文从销售商角度出发，利用逆向思维法进行分析求解。对式(2)求关于 p和t的一阶偏导为

Hessian矩阵负定，即 f存在极大值点，令式(8)、(9)为零，即可得制造商关于批发价与回购价最优决策组合为

再将式(12)和式(13)代入 pr表达式中，即可得销售商最优回收价为

将 pr∗代入 Q的表达式中，即可得销售商最优回收量为

3.2 联合决策

供应链是由相互依存、相互关系的上下游企业构成的，在进行决策时，由于理性经济人的假设，供应链企业决策均是以自身利益最大化为依据，故而分散决策下的最优并不一定是整体的最优。联合决策下，供应链企业构成利益共同体，不考虑奖励函数，销售商会在回收过程中进行质量投入，以此来提高回收品质量水平，使供应链整体效益最大化。据上述，构建联合决策条件下制造商的期望利润函数为

Hessian矩阵负定，即 f是关于 p 、 pr的凸函数，且存在极大值点，令式(21)、(22)为零，即可得供应链关于售价与回收价最优决策组合为

4 算例分析

对模型中的有关参数进行赋值，令h=40，k=3.5，p0=12，Cm=220，α=2 500 ，β=2 ，η=2，ξ=120，s=100，λ=200。

4.1 回收质量对分散决策的影响

考虑回收品质量从0.1到0.9，分散决策条件下各节点企业的决策结果如表2所示。

表 2 分散决策下各参数结果Table 2 Results of parameters under decentralized decision

对比联合决策下的计算结果可以看出，分散决策下各指数与联合决策下的各指数表现出一致的变化趋势：回收品质量水平不影响产品市场售价，但随着回收品质量水平的提高，回收价、销售商利润、制造商利润以及供应链整体利润均提高，再制品产量增加，新产品产量减少。其中，当q=0.1时，pr＜0，表明在该质量水平下，回收商的回收活动是明显亏损的，因此实际情况表现为不会进行回收活动。

4.2 回收质量对联合决策的影响

考虑回收品质量从0.1到0.9，联合决策条件下各节点企业的决策结果如表3所示。

表 3 联合决策下各参数结果Table 3 Results of parameters under joint decision

由表3可以明显看出，回收品质量不会对正向供应链中销售商定价决策活动产生作用，但回收品质量与回收价、整体利润呈正相关。此外，产品的最优生产决策也发生了变化，随着回收品质量的提高，回收价提高，回收商获取的奖励增加，则会有更多高质量的废旧品被回收用于再制造，由此就出现了再制品产量增加及新产品产量减少的现象。回收品质量提高，使得制造商再制造过程中会节约更多的生产成本，供应链整体利润增加，市场会得到良性促进，从而供应链企业会投入更多的回收成本来回收更多更高质量的废旧品，表现在回收价格提高。

根据表2和表3数据模拟得出的各变量与回收品质量之间的关系，如图2所示。

从图2中可以明显看出，回收品质量水平的变化并不会影响到产品的市场售价；回收品质量的变化会影响制造商生产决策，回收品质量提高，会出现“再制品增，新产品减”的现象。此外，2种决策条件下，供应链利润都随回收品质量的提高而增加，从而促使供应链企业提高废旧产品回收价以回收更多高质量的废旧品，市场会得到良性促进。另外还可以判断联合决策下的再制造闭环供应链各项决策总是优于分散决策下的情形，制造商与销售商的各自决策并没有使其达到利润最大化。由图2(f)的变化趋势可以看出，质量可控情境下，随着回收品质量的提高，制造商和销售商的利润也都在增加，故而销售商和制造商均有动力去回收再制造更高质量的废旧品。进一步观察图2(a)～(e)的变化趋势，可以发现，联合决策下由于回收品质量变化导致的供应链企业决策波动更为明显，即联合决策下供应链企业对于回收品质量变化感知更为敏感，从而作出更为合理的决策反应。

图 2 回收品质量对各参数的影响Figure 2 Effect of recovery quality on parameters.

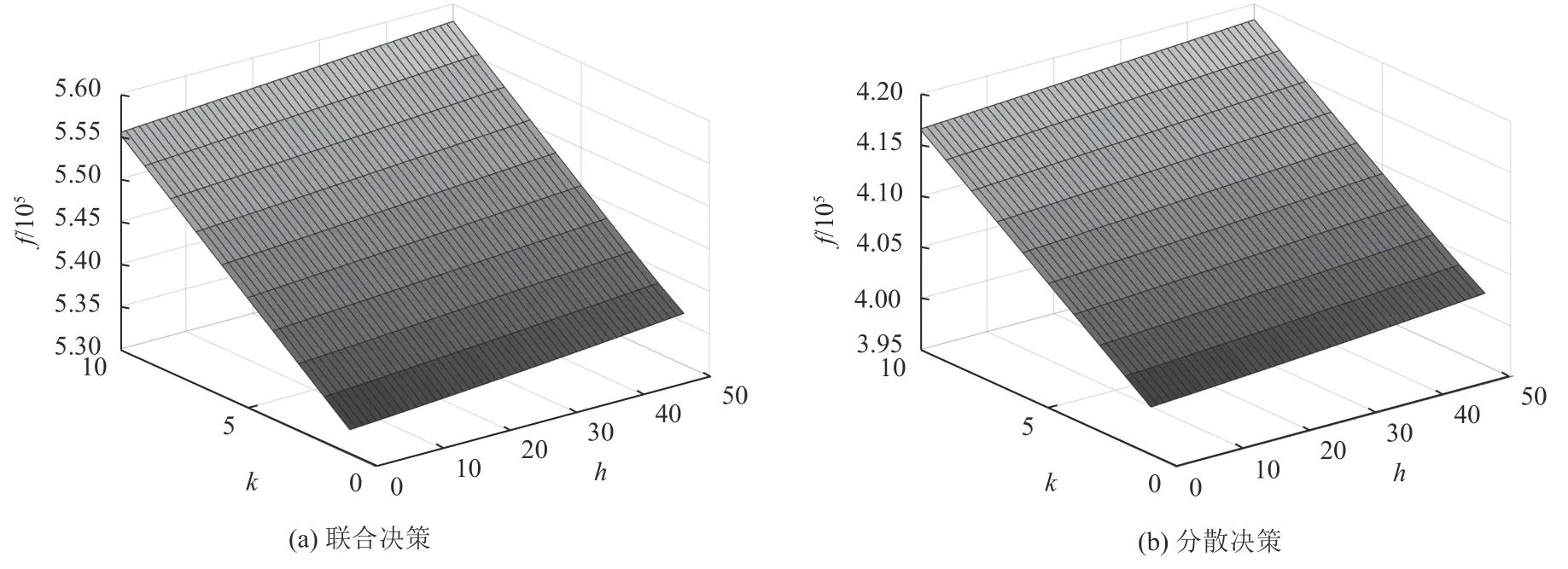
图 3 2种决策下绿色偏好与价格偏好对总利润的影响Figure 3 Effect of green preference and price preference on total profit under two decisions

4.3 敏感性分析

取q=0.5，分析h∈(0,50)，k∈(0,10)时，2种决策条件下消费者绿色偏好、回收价格偏好与供应链企业利润之间的关系。利用Matlab软件进行模拟仿真，得出联合与分散2种决策条件下，供应链整体利润函数如图3所示。从图3可以看出，消费者绿色偏好、价格偏好与供应链企业利润间均存在正向关系，即消费者绿色偏好越强，价格偏好越高，供应链整体利润则越大。这主要是因为，消费者绿色偏好意识增强，会有更多高质量的废旧品被回收再制造；消费者价格偏好扩大，从而使得回收品质量水平提高，回收价格增加，彼此促进，供应链利润扩大。

5 结论

本文基于回收品质量可控这一情境，引入质量投入和奖励函数对销售商回收过程中回收品质量进行引导与控制，在此基础上构建闭环供应链两级博弈模型，采用逆向归纳法对模型进行求解分析，并研究考虑回收品质量可控的再制造闭环供应链的生产及定价决策问题，进一步分析了废旧品质量对供应链企业定价、生产决策以及效益的影响。

主要结论如下。1) 不论是分散决策或是联合决策，回收价、供应链企业利润都与回收品质量正相关，市场得到良性促进，企业会提高回收价以回收更多更高质量水平的废旧品，从而出现了再制品量增加，新产品量减少的现象。2) 2种决策条件下，回收品质量水平对供应链企业各参数的影响基本一致，但是联合决策下供应链的总利润、回收价、零售价等参数都始终优于分散决策下的情形。此外，联合决策条件下企业对于决策过程中有关影响因素的变化波动更为敏感，具有更高的抗风险能力。3) 消费者绿色偏好与回收价格偏好能够对供应链利润产生积极影响。消费者绿色偏好与回收价格偏好的提高，不仅能扩大供应链企业的经济收益，同时也能有效提高社会环境效益。